数据结构与算法:17 图
17 图
知识结构:
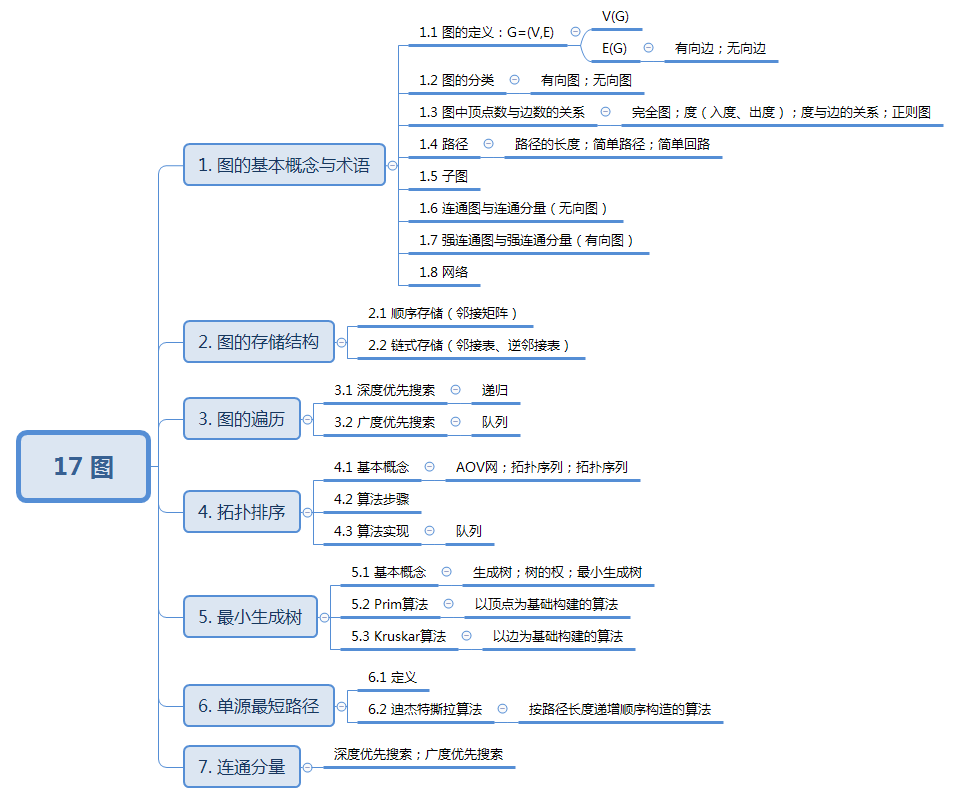
1. 图的基本概念与术语
1.1 图的定义
图由顶点集和边集组成,记为G=(V,E)G=(V,E)G=(V,E)。
- 顶点集:顶点的有穷非空集合,记为V(G)V(G)V(G)。
- 边集:顶点偶对的有穷集合,记为E(G)E(G)E(G) 。
边:
- 无向边:(vi,vj)=(vj,vi)(v_i,v_j)=(v_j,v_i)(vi,vj)=(vj,vi)
- 有向边(弧):<vi,vj>≠<vj,vi><v_i,v_j> \neq <v_j,v_i><vi,vj>=<vj,vi> 始点viv_ivi称为弧尾,终点vjv_jvj称为弧头。
例题:

例题:
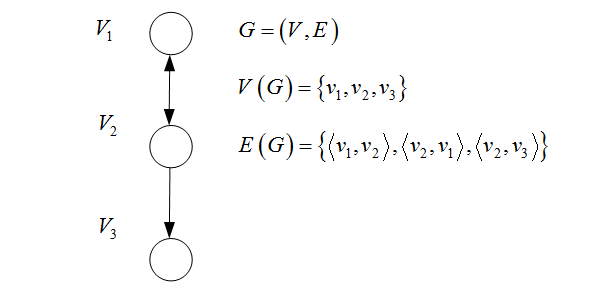
1.2 图的分类
- 有向图:E(G)E(G)E(G)由有向边构成。
- 无向图:E(G)E(G)E(G)由无向边构成。
1.3 图中顶点数与边数的关系
(1)设顶点数为nnn,边数为eee则:
- 无向图:0≤e≤n(n−1)20\leq e \leq \frac{n(n-1)}{2}0≤e≤2n(n−1),e=n(n−1)2e=\frac{n(n-1)}{2}e=2n(n−1)的图称为无向完全图。
- 有向图:0≤e≤n(n−1)0\leq e \leq n(n-1)0≤e≤n(n−1),e=n(n−1)e = n(n-1)e=n(n−1)的图称为有向完全图。
(2)顶点的度
- 无向图:D(v)=D(v)=D(v)=与vvv连接的边数。
- 有向图:D(v)=ID(v)+OD(v)D(v)=ID(v)+OD(v)D(v)=ID(v)+OD(v)
- ID(v)ID(v)ID(v):以vvv为终点(弧头)的边数。
- OD(v)OD(v)OD(v):以vvv为起点(弧尾)的边数。
(3)度与边的关系
e=∑i=1nD(vi)2e=\frac{\sum_{i=1}^{n}D(v_i)}{2} e=2∑i=1nD(vi)
(4)正则图:所有顶点的度都相同的图
1.4 路径
(1)定义:图G=(V,E)G=(V,E)G=(V,E),若存在一个顶点序列vp,vi1,vi2,⋯,vim,vqv_p,v_{i1},v_{i2},\cdots,v_{im},v_qvp,vi1,vi2,⋯,vim,vq,使得(vp,vi1),(vi1,vi2),⋯,(vim,vq)∈E(G)(v_p,v_{i1}),(v_{i1},v_{i2}),\cdots,(v_{im},v_q)\in E(G)(vp,vi1),(vi1,vi2),⋯,(vim,vq)∈E(G)(无向图)或者<vp,vi1>,<vi1,vi2>,⋯,<vim,vq>∈E(G)<v_p,v_{i1}>,<v_{i1},v_{i2}>,\cdots,<v_{im},v_q>\in E(G)<vp,vi1>,<vi1,vi2>,⋯,<vim,vq>∈E(G)(有向图)则称vpv_pvp到vqv_qvq存在一条路径。
(2)路径的长度:路径上边的数目。
(3)简单路径:若一条路径上除vpv_pvp,vqv_qvq可相同外,其余顶点均不相同的路径。
(4)简单回路:vpv_pvp与vqv_qvq相同的简单路径。
1.5 子图
设G=(V,E)G=(V,E)G=(V,E)是一个图,若V′⊆VV'\subseteq VV′⊆V,E′⊆EE'\subseteq EE′⊆E且E′E^{'}E′中的边所关联的顶点∈V′\in V'∈V′,则G′=(V′,E′)G'=(V',E')G′=(V′,E′) 也是一个图,并称其为GGG的子图。

1.6 连通图与连通分量(无向图)
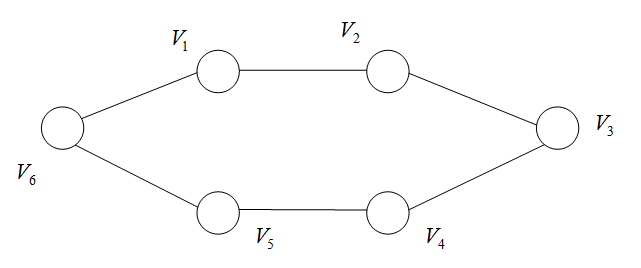
连通图:无向图GGG的V(G)V(G)V(G)中,任何两个顶点都存在路径,则称GGG为连通图。
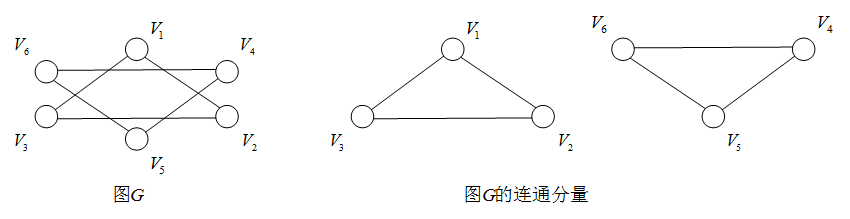
连通分量:无向图GGG的极大连通子图。
注:
- 连通图的连通分量只有一个,为其本身。
- 非连通图的连通分量不唯一。
例子:
1.7 强连通图与强连通分量(有向图)
强连通图:有向图GGG的V(G)V(G)V(G)中,任何两个顶点都存在路径,则称GGG为强连通图。
强连通分量:有向图GGG的极大连通子图。
注:
- 强连通图的强连通分量只有一个,为其本身。
- 非强连通图的强连通分量不唯一。
例子:

1.8 网络
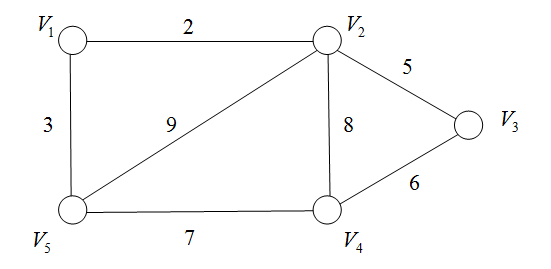
E(G)E(G)E(G)中的每条边都带有权值的图称为网络。
注:权一般具有实际意义,比如距离、消耗等。
例子:
2. 图的存储结构
2.1 顺序存储(邻接矩阵)
邻接矩阵:表示顶点之间相邻关系的矩阵
若图G=(V,E)G=(V,E)G=(V,E),则其邻接矩阵可表示为:
A[i,j]=={1,(vi,vj)∈E(G)or<vi,vj>∈E(G)0,(vi,vj)∉E(G)or<vi,vj>∉E(G)A[i,j]==\begin{cases} 1, & (v_i,v_j)\in E(G) or <v_i,v_j>\in E(G)\\ 0, & (v_i,v_j)\notin E(G) or <v_i,v_j>\notin E(G) \end{cases} A[i,j]=={1,0,(vi,vj)∈E(G)or<vi,vj>∈E(G)(vi,vj)∈/E(G)or<vi,vj>∈/E(G)
例子:无向图的存储
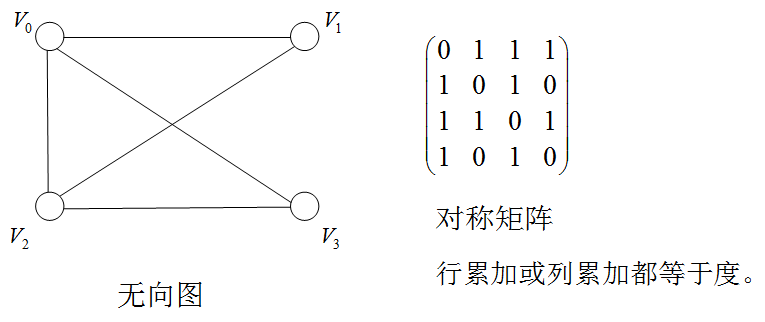
例子:有向图的存储
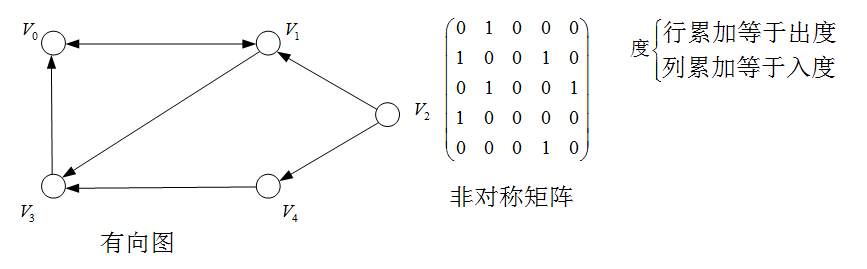
若图G=(V,E)G=(V,E)G=(V,E)为网络,则其邻接矩阵可表示为:
A[i,j]=={ωij,(vi,vj)∈E(G)or<vi,vj>∈E(G)0or∞,(vi,vj)∉E(G)or<vi,vj>∉E(G)A[i,j]==\begin{cases} \omega_{ij}, & (v_i,v_j)\in E(G) or <v_i,v_j>\in E(G)\\ 0 or \infty, & (v_i,v_j)\notin E(G) or <v_i,v_j>\notin E(G) \end{cases} A[i,j]=={ωij,0or∞,(vi,vj)∈E(G)or<vi,vj>∈E(G)(vi,vj)∈/E(G)or<vi,vj>∈/E(G)
例子:网络的存储
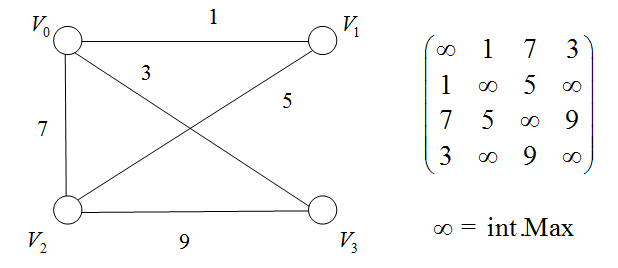
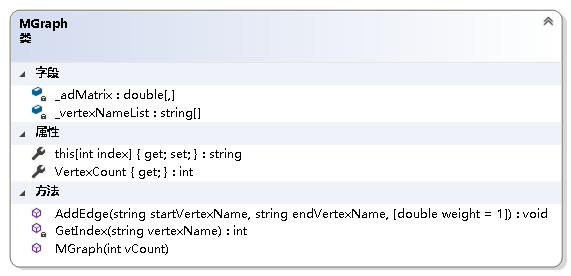
using System;
namespace NonLinearStruct.Graph
{/// <summary>/// 图抽象数据类型实现--利用邻接矩阵/// </summary>public class MGraph{private readonly double[,] _adMatrix;//邻接矩阵private readonly string[] _vertexNameList;//存储图中各结点名字的数组/// <summary>/// 获取图中结点的个数/// </summary>public int VertexCount { get; }/// <summary>/// 初始化MGraph类的新实例/// </summary>/// <param name="vCount">图中结点的个数</param>public MGraph(int vCount){if (vCount <= 0)throw new ArgumentOutOfRangeException();VertexCount = vCount;_vertexNameList = new string[vCount];_adMatrix = new double[vCount, vCount];}/// <summary>/// 获取或设置图中各结点的名称/// </summary>/// <param name="index">结点名称从零开始的索引</param>/// <returns>指定索引处结点的名称</returns>public string this[int index]{get{if (index < 0 || index > VertexCount - 1)throw new IndexOutOfRangeException();return _vertexNameList[index];}set{if (index < 0 || index > VertexCount - 1)throw new IndexOutOfRangeException();_vertexNameList[index] = value;}}private int GetIndex(string vertexName){//根据结点名字获取结点在数组中的下标int i;for (i = 0; i < VertexCount; i++){if (_vertexNameList[i] == vertexName)break;}return i == VertexCount ? -1 : i;}/// <summary>/// 给邻接矩阵赋值/// </summary>/// <param name="startVertexName">起始结点的名字</param>/// <param name="endVertexName">终止结点的名字</param>/// <param name="weight">边上的权值或连接关系</param>public void AddEdge(string startVertexName, string endVertexName, double weight = 1){int i = GetIndex(startVertexName);int j = GetIndex(endVertexName);if (i == -1 || j == -1)throw new Exception("图中不存在该边.");_adMatrix[i, j] = weight;}}
}
2.2 链式存储(邻接表)
邻接表:由顺序存储的顶点表和链式存储的边表构成的图的存储结构。
例子:无向图的存储
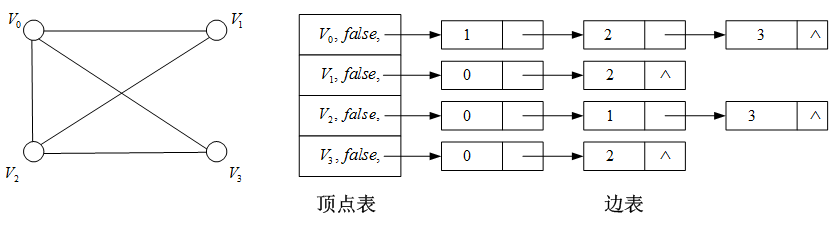
例子:有向图的存储
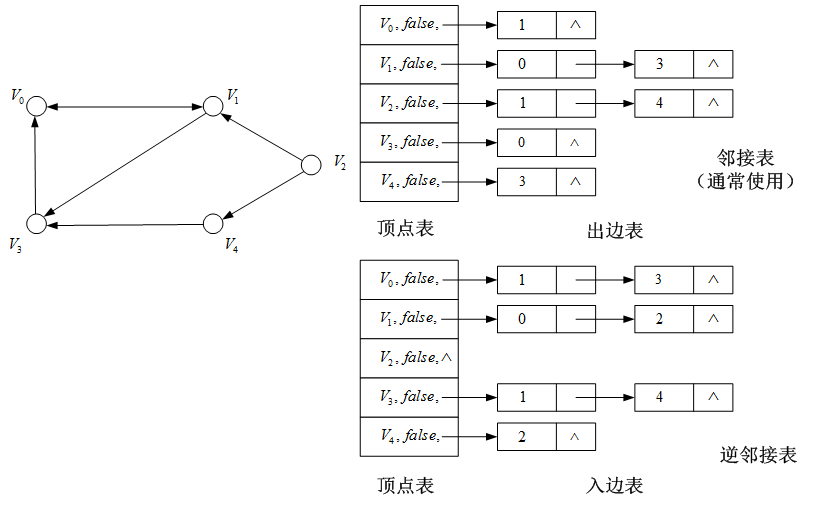
例子:网络的存储
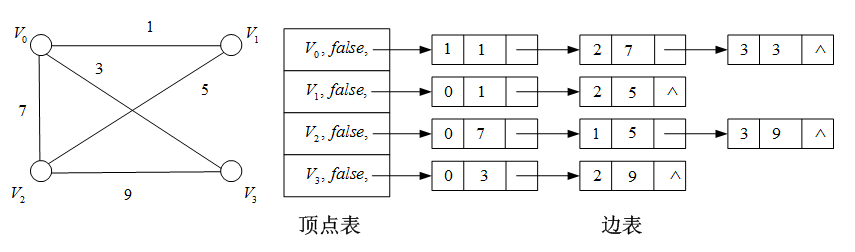
边表结点的实现:

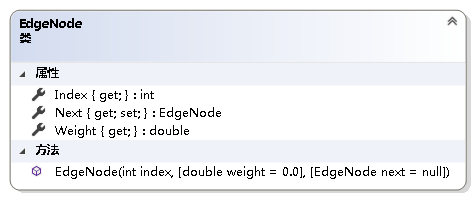
using System;
namespace NonLinearStruct.Graph
{/// <summary>/// 邻接表边表上的结点/// </summary>public class EdgeNode{/// <summary>/// 获取边终点在顶点数组中的位置/// </summary>public int Index { get; }/// <summary>/// 获取边上的权值/// </summary>public double Weight { get; }/// <summary>/// 获取或设置下一个邻接点/// </summary>public EdgeNode Next { get; set; }/// <summary>/// 初始化EdgeNode类的新实例/// </summary>/// <param name="index">边终点在顶点数组中的位置</param>/// <param name="weight">边上的权值</param>/// <param name="next">下一个邻接点</param>public EdgeNode(int index, double weight = 0.0, EdgeNode next = null){if (index < 0)throw new ArgumentOutOfRangeException();Index = index;Weight = weight;Next = next;}}
}顶点表结点的实现:


namespace NonLinearStruct.Graph
{/// <summary>/// 邻接表顶点表中的结点/// </summary>public class VertexNode{/// <summary>/// 获取或设置顶点的名字/// </summary>public string VertexName { get; set; }/// <summary>/// 获取或设置顶点是否被访问/// </summary>public bool Visited { get; set; }/// <summary>/// 获取或设置顶点的第一个邻接点/// </summary>public EdgeNode FirstNode { get; set; }/// <summary>/// 初始化VertexNode类的新实例/// </summary>/// <param name="vName">顶点的名字</param>/// <param name="firstNode">顶点的第一个邻接点</param>public VertexNode(string vName, EdgeNode firstNode = null){VertexName = vName;Visited = false;FirstNode = firstNode;}}
}
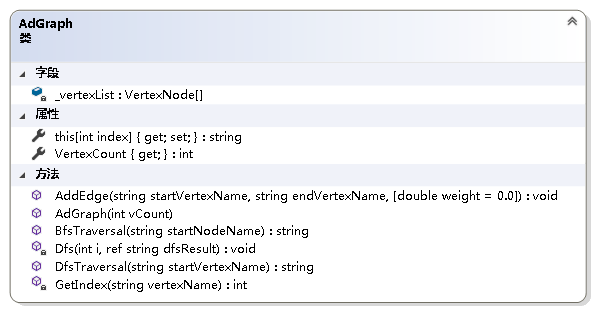
图结构的实现
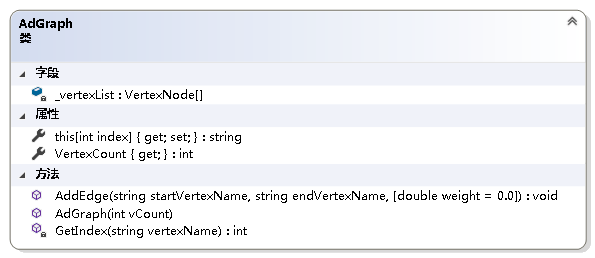
using System;
using System.Collections.Generic;
using System.Linq;
using LinearStruct;namespace NonLinearStruct.Graph
{/// <summary>/// 图抽象数据类型实现--利用邻接表/// </summary>public class AdGraph{private readonly VertexNode[] _vertexList; //结点表/// <summary>/// 获取图的结点数/// </summary>public int VertexCount { get; }/// <summary>/// 初始化AdGraph类的新实例/// </summary>/// <param name="vCount">图中结点的个数</param>public AdGraph(int vCount){if (vCount <= 0)throw new ArgumentOutOfRangeException();VertexCount = vCount;_vertexList = new VertexNode[vCount];}/// <summary>/// 获取或设置图中各结点的名称/// </summary>/// <param name="index">结点名称从零开始的索引</param>/// <returns>指定索引处结点的名称</returns>public string this[int index]{get{if (index < 0 || index > VertexCount - 1)throw new ArgumentOutOfRangeException();return _vertexList[index] == null? "NULL": _vertexList[index].VertexName;}set{if (index < 0 || index > VertexCount - 1)throw new ArgumentOutOfRangeException();if (_vertexList[index] == null)_vertexList[index] = new VertexNode(value);else_vertexList[index].VertexName = value;}}/// <summary>/// 得到结点在结点表中的位置/// </summary>/// <param name="vertexName">结点的名称</param>/// <returns>结点的位置</returns>private int GetIndex(string vertexName){int i;for (i = 0; i < VertexCount; i++){if (_vertexList[i] != null && _vertexList[i].VertexName == vertexName)break;}return i == VertexCount ? -1 : i;}/// <summary>/// 给图加边/// </summary>/// <param name="startVertexName">起始结点的名字</param>/// <param name="endVertexName">终止结点的名字</param>/// <param name="weight">边上的权值</param>public void AddEdge(string startVertexName, string endVertexName, double weight = 0.0){int i = GetIndex(startVertexName);int j = GetIndex(endVertexName);if (i == -1 || j == -1)throw new Exception("图中不存在该边.");EdgeNode temp = _vertexList[i].FirstNode;if (temp == null){_vertexList[i].FirstNode = new EdgeNode(j, weight);}else{while (temp.Next != null)temp = temp.Next;temp.Next = new EdgeNode(j, weight);}}}
}
3. 图的遍历
3.1 深度优先搜索
算法:
假设G=(V,E)G=(V,E)G=(V,E)以SSS为起点(源点)进行搜索。
首先标识SSS为已访问结点,接着寻找与SSS相邻的结点ω\omegaω,若ω\omegaω是未被访问结点,则以ω\omegaω为起点进行深度优先搜索,若ω\omegaω是已被访问结点,则寻找其它与SSS相邻的结点,直到与SSS有路径相通的所有结点都被访问过。
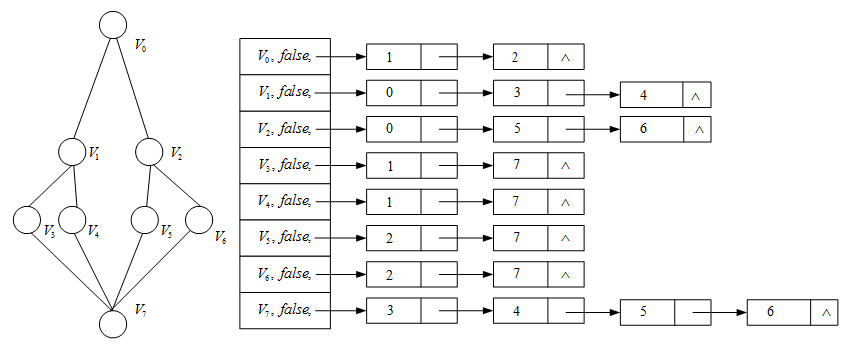
例子:

深度优先搜索的序列为:V0,V1,V3,V7,V4,V5,V2,V6V_0,V_1,V_3,V_7,V_4,V_5,V_2,V_6V0,V1,V3,V7,V4,V5,V2,V6
虽然遍历序列不唯一,但是邻接表确定后,遍历序列就唯一了。
实现:
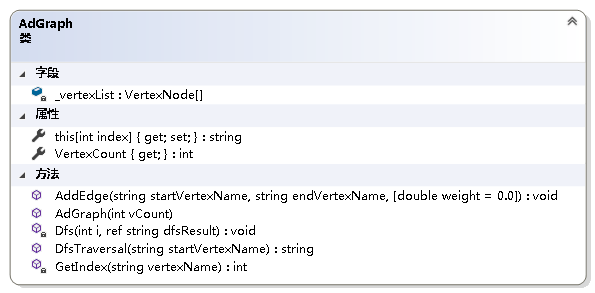
private void Dfs(int i, ref string dfsResult)
{//深度优先搜索递归函数_vertexList[i].Visited = true;dfsResult += _vertexList[i].VertexName + "\n";EdgeNode p = _vertexList[i].FirstNode;while (p != null){if (_vertexList[p.Index].Visited)p = p.Next;elseDfs(p.Index, ref dfsResult);}
}/// <summary>
/// 得到深度优先搜索序列
/// </summary>
/// <param name="startVertexName">进行深度优先搜索的起始点名称</param>
/// <returns>深度优先搜索序列</returns>
public string DfsTraversal(string startVertexName)
{string dfsResult = string.Empty;int i = GetIndex(startVertexName);if (i != -1){for (int j = 0; j < VertexCount; j++)_vertexList[j].Visited = false;Dfs(i, ref dfsResult);}return dfsResult;
}
3.2 广度优先搜索
算法:
假设G=(V,E)G=(V,E)G=(V,E)以SSS为起点(源点)进行搜索。
首先标识SSS为已访问结点,接着访问SSS的邻接点ω1,ω2,⋯,ωt\omega_1,\omega_2,\cdots,\omega_tω1,ω2,⋯,ωt然后访问ω1,ω2,⋯,ωt\omega_1,\omega_2,\cdots,\omega_tω1,ω2,⋯,ωt的未被访问的邻接点,以此类推,直到与SSS有路径相连的所有结点都被访问到。
先来先服务的思想。
例子:
深度优先搜索的序列为:V0,V1,V2,V3,V4,V5,V6,V7V_0,V_1,V_2,V_3,V_4,V_5,V_6,V_7V0,V1,V2,V3,V4,V5,V6,V7
虽然遍历序列不唯一,但是邻接表确定后,遍历序列就唯一了。
实现:
/// <summary>
/// 得到广度优先搜索序列
/// </summary>
/// <param name="startNodeName">进行广度优先搜索的起始点名称</param>
/// <returns>广度优先搜索序列</returns>
public string BfsTraversal(string startNodeName)
{string bfsResult = string.Empty;int i = GetIndex(startNodeName);if (i != -1){for (int j = 0; j < VertexCount; j++)_vertexList[j].Visited = false;_vertexList[i].Visited = true;bfsResult += _vertexList[i].VertexName + "\n";LinkQueue<int> lq = new LinkQueue<int>();lq.EnQueue(i);while (lq.IsEmpty() == false){int j = lq.QueueFront;lq.DeQueue();EdgeNode p = _vertexList[j].FirstNode;while (p != null){if (_vertexList[p.Index].Visited == false){_vertexList[p.Index].Visited = true;bfsResult += _vertexList[p.Index].VertexName + "\n";lq.EnQueue(p.Index);}p = p.Next;}}}return bfsResult;
}
4. 拓扑排序
4.1 基本概念
AOVAOVAOV网(Activity on Vertex Network):用顶点表示活动,用有向边表示活动之间先后关系的有向图。
拓扑序列:把AOVAOVAOV网中的所有顶点排成一个线性序列,使每个活动的所有前驱活动都排在该活动的前边。
拓扑排序:构造AOVAOVAOV网拓扑序列的过程。
例题:按照拓扑排序安排下列课程
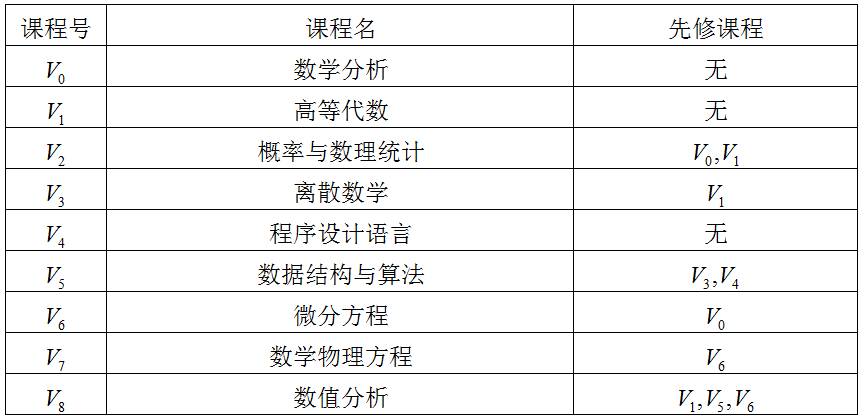
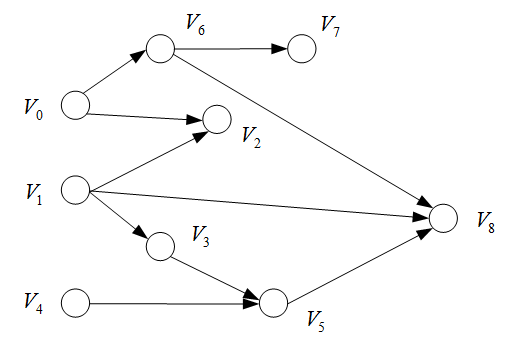
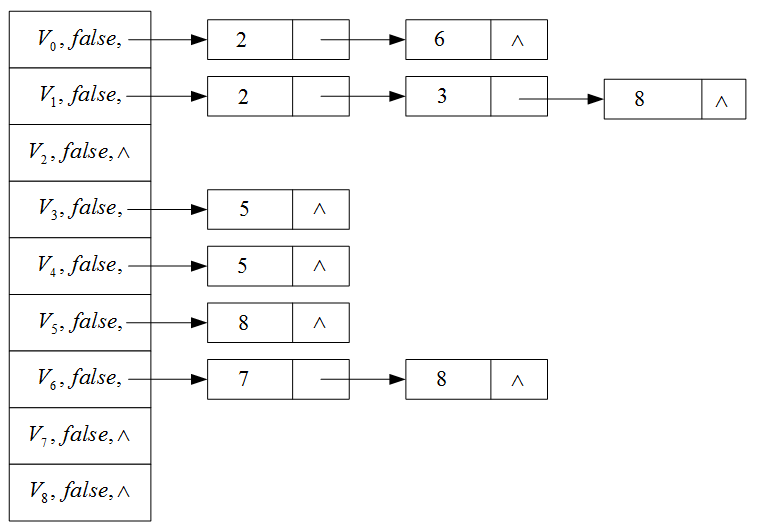
4.2 算法步骤
第1步:从网中选择一个入度为0的顶点加入排序序列。
第2步:从网中删除该顶点及其所有出边。
第3步:执行第1、2步,直到所有顶点已排序或网中剩余顶点入度均不为0(说明:网中存在回路,无法继续拓扑排序)。
拓扑序列:
(1)V0,V1,V4,V6,V2,V3,V7,V5,V8V_0,V_1,V_4,V_6,V_2,V_3,V_7,V_5,V_8V0,V1,V4,V6,V2,V3,V7,V5,V8
(2)V0,V6,V1,V2,V3,V4,V5,V8,V7V_0,V_6,V_1,V_2,V_3,V_4,V_5,V_8,V_7V0,V6,V1,V2,V3,V4,V5,V8,V7
注:对于任何无回路的AOVAOVAOV网,其顶点均可排成拓扑序列,但其拓扑序列未必唯一。
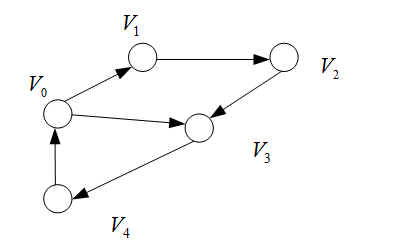
存在回路的有向图,不能构成拓扑序列。
4.3 算法实现
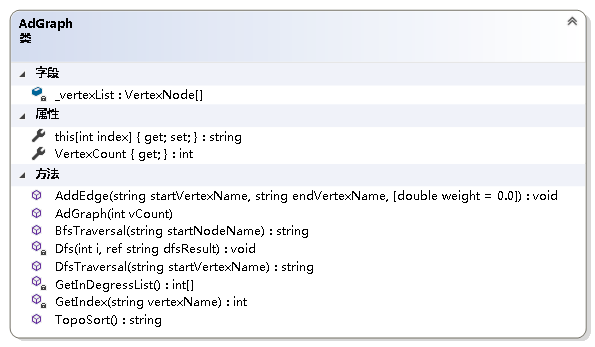
/// <summary>
/// 得到每个节点的入度
/// </summary>
/// <returns></returns>
private int[] GetInDegressList()
{int[] id = new int[VertexCount];for (int i = 0; i < VertexCount; i++){EdgeNode p = _vertexList[i].FirstNode;while (p != null){id[p.Index]++;p = p.Next;}}return id;
}/// <summary>
/// 得到AOV网的拓扑排序序列
/// </summary>
/// <returns>AOV网的拓扑排序序列</returns>
public string TopoSort()
{string result = string.Empty;int[] id = GetInDegressList();LinkQueue<int> lq = new LinkQueue<int>();for (int i = 0; i < VertexCount; i++){if (id[i] == 0)lq.EnQueue(i);}if (lq.Length == VertexCount)throw new Exception("此有向图无有向边.");while (lq.IsEmpty() == false){int j = lq.QueueFront;lq.DeQueue();result += _vertexList[j].VertexName + "\n";EdgeNode p = _vertexList[j].FirstNode;while (p != null){id[p.Index]--;if (id[p.Index] == 0){lq.EnQueue(p.Index);}p = p.Next;}}int k;for (k = 0; k < VertexCount; k++){if (id[k] != 0){break;}}return (k == VertexCount) ? result : "该AOV网有环.";
}
5. 最小生成树
5.1 基本概念
生成树:设GGG为连通网,具有GGG的所有顶点(nnn个)且只有n−1n-1n−1条边的连通子网。
树的权:生成树TTT的各边的权值总和。
最小生成树:权值最小的生成树。
5.2 Prim算法
算法原理(贪心算法):
设G=(V,E)G=(V,E)G=(V,E)为连通网,T=(U,TE)T=(U,TE)T=(U,TE)为其对应的最小生成树,从v0v_0v0开始构造。
(1)开始时,U={u0=v0}U = \lbrace u_0=v_0 \rbraceU={u0=v0},TE=ΦTE=\PhiTE=Φ。
(2)找到满足weight(u,v)=min{weight(ui,vj)∣ui∈U,vj∈V−U}weight(u,v)=min \lbrace weight(u_i,v_j)|u_i \in U,v_j\in V-U \rbraceweight(u,v)=min{weight(ui,vj)∣ui∈U,vj∈V−U}的边,把它并入TETETE中,vvv同时并入UUU。
(3)反复执行(2),直到U=VU=VU=V时,终止算法。
例题:
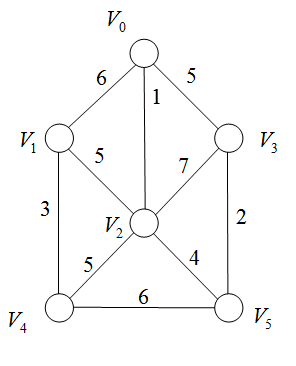

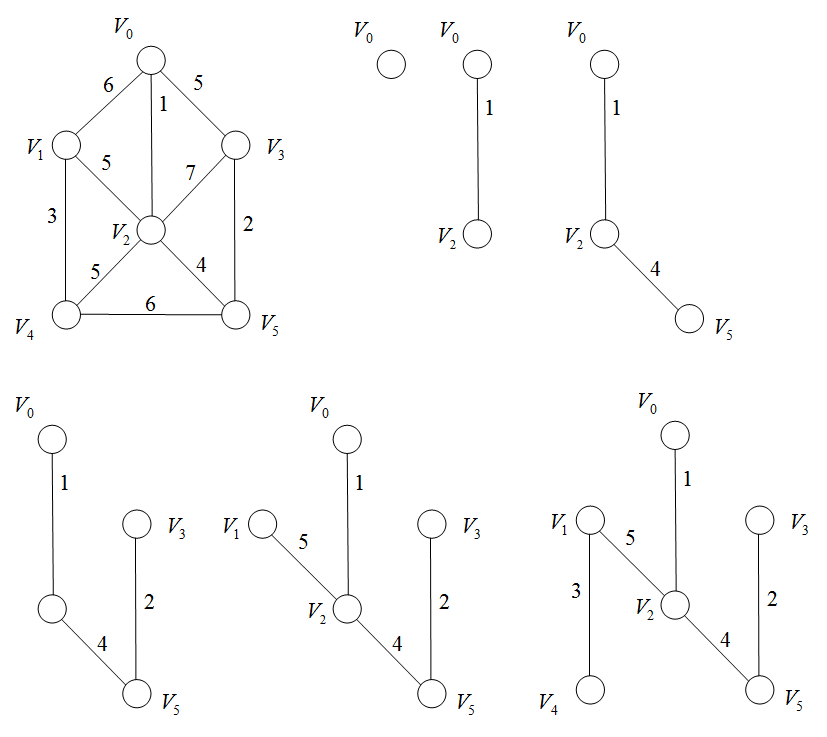
算法实现:
最小生成树结点的存储:


using System;namespace NonLinearStruct
{/// <summary>/// 生成树结点的抽象数据类型/// </summary>public class SpanTreeNode{/// <summary>/// 获取或设置结点本身的名称/// </summary>public string SelfName { get; }/// <summary>/// 获取或设置结点双亲的名称/// </summary>public string ParentName { get; }/// <summary>/// 获取或设置边的权值/// </summary>public double Weight { get; set; }/// <summary>/// 构造SpanTreeNode实例/// </summary>/// <param name="selfName">结点本身的名称</param>/// <param name="parentName">结点双亲的名称</param>/// <param name="weight">边的权值</param>public SpanTreeNode(string selfName, string parentName, double weight){if (string.IsNullOrEmpty(selfName) || string.IsNullOrEmpty(parentName))throw new ArgumentNullException();SelfName = selfName;ParentName = parentName;Weight = weight;}}
}
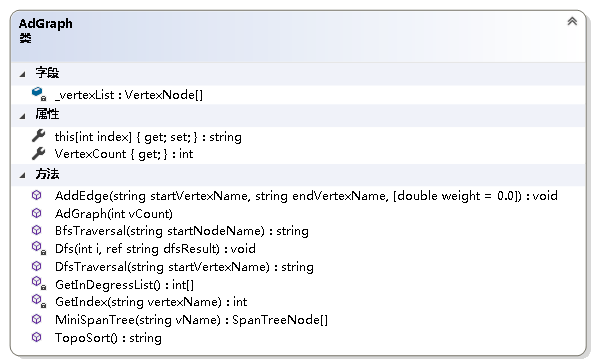
/// <summary>
/// 得到连通网的最小生成树Prim算法
/// </summary>
/// <param name="vName">树根结点</param>
/// <returns>连通网的最小生成树</returns>
public SpanTreeNode[] MiniSpanTree(string vName)
{int i = GetIndex(vName);if (i == -1)return null;SpanTreeNode[] spanTree = new SpanTreeNode[VertexCount];spanTree[0] = new SpanTreeNode(_vertexList[i].VertexName, "NULL", 0.0);//U中结点到各结点最小权值那个结点在VertexList中的索引号int[] vertexIndex = new int[VertexCount];//U中结点到各个结点的最小权值double[] lowCost = new double[VertexCount];for (int j = 0; j < VertexCount; j++){lowCost[j] = double.MaxValue;vertexIndex[j] = i;}EdgeNode p1 = _vertexList[i].FirstNode;while (p1 != null){lowCost[p1.Index] = p1.Weight;p1 = p1.Next;}vertexIndex[i] = -1;for (int count = 1; count < VertexCount; count++){double min = double.MaxValue;int v = i;for (int k = 0; k < VertexCount; k++){if (vertexIndex[k] != -1 && lowCost[k] < min){min = lowCost[k];v = k;}}spanTree[count] = new SpanTreeNode(_vertexList[v].VertexName, _vertexList[vertexIndex[v]].VertexName, min);vertexIndex[v] = -1;EdgeNode p2 = _vertexList[v].FirstNode;while (p2 != null){if (vertexIndex[p2.Index] != -1 && p2.Weight < lowCost[p2.Index]){lowCost[p2.Index] = p2.Weight;vertexIndex[p2.Index] = v;}p2 = p2.Next;}}return spanTree;
}
5.3 Kruskar算法
设G=(V,E)G=(V,E)G=(V,E)为连通网,TTT为其对应的最小生成树。
(1)初始时T={V,{Φ}}T=\lbrace V, \lbrace \Phi \rbrace \rbraceT={V,{Φ}},即TTT中没有边,只有nnn个顶点,就是nnn个连通分量。
(2)在EEE中选择权值最小的边(u,v)(u,v)(u,v),并将此边从EEE中删除。
(3)如果uuu,vvv在TTT的不同的连通分量中,则将(u,v)(u,v)(u,v)加入到TTT中,从而导致TTT中减少一个连通分量。
(4)反复执行(2)(3)直到TTT中仅剩一个连通分量时,终止操作。
例题:
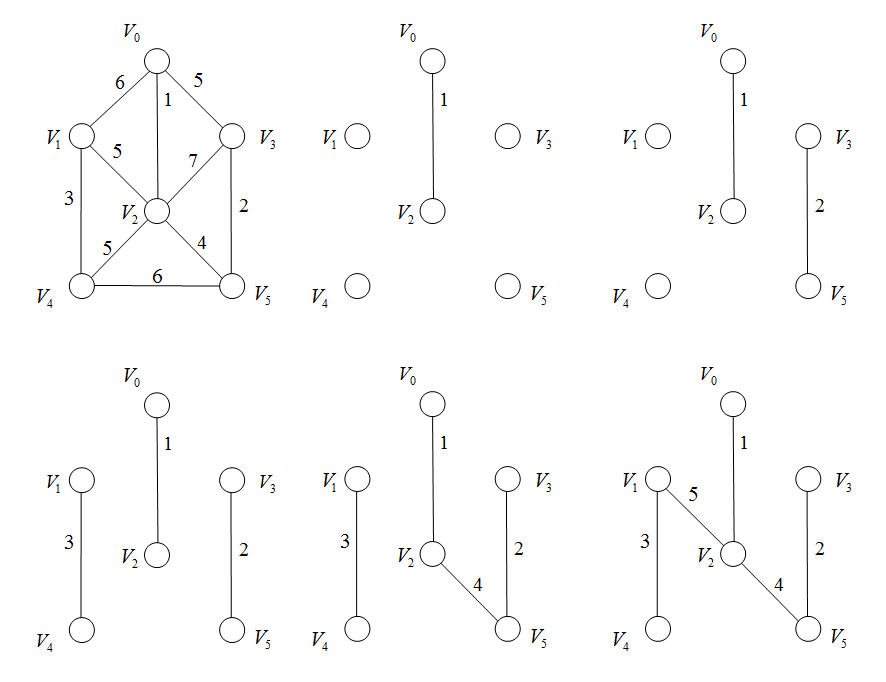
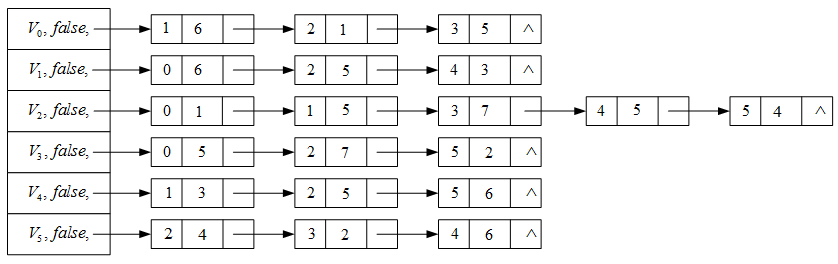
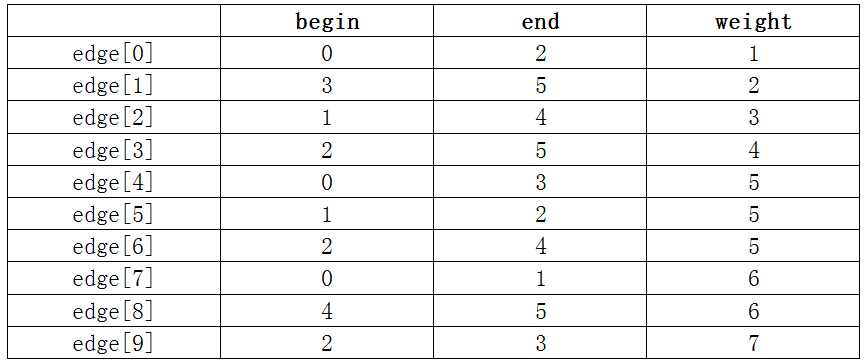
算法实现:

namespace NonLinearStruct.Graph
{/// <summary>/// 表示图的边/// </summary>public class Edge{/// <summary>/// 起点编号/// </summary>public int Begin { get; }/// <summary>/// 终点编号/// </summary>public int End { get; }/// <summary>/// 权值/// </summary>public double Weight { get; }/// <summary>/// 创建一个 Edge 类的新实例/// </summary>/// <param name="begin">起点编号</param>/// <param name="end">终点编号</param>/// <param name="weight">权值</param>public Edge(int begin, int end, double weight = 0.0){Begin = begin;End = end;Weight = weight;}}
}
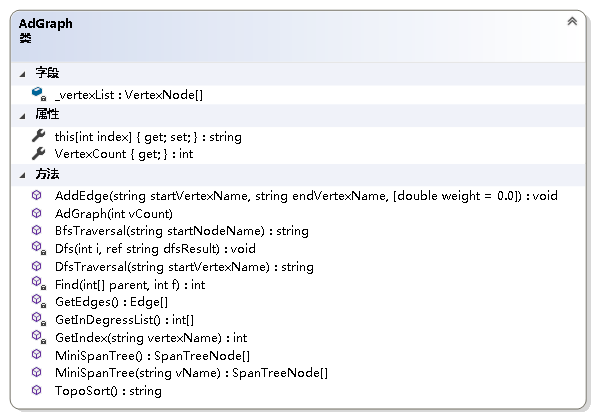
private Edge[] GetEdges()
{for (int i = 0; i < VertexCount; i++)_vertexList[i].Visited = false;List<Edge> result = new List<Edge>();for (int i = 0; i < VertexCount; i++){_vertexList[i].Visited = true;EdgeNode p = _vertexList[i].FirstNode;while (p != null){if (_vertexList[p.Index].Visited == false){Edge edge = new Edge(i, p.Index, p.Weight);result.Add(edge);}p = p.Next;}}return result.OrderBy(a => a.Weight).ToArray();
}private int Find(int[] parent, int f)
{while (parent[f] > -1)f = parent[f];return f;
}/// <summary>
/// 克鲁斯卡尔算法 最小生成树
/// </summary>
/// <returns></returns>
public SpanTreeNode[] MiniSpanTree()
{int[] parent = new int[VertexCount];for (int i = 0; i < VertexCount; i++){parent[i] = -1;}SpanTreeNode[] tree = new SpanTreeNode[VertexCount];Edge[] edges = GetEdges();int count = 1;for (int i = 0; i < edges.Length; i++){int begin = edges[i].Begin;int end = edges[i].End;int b = Find(parent, begin);int e = Find(parent, end);if (b != e){parent[e] = b;tree[count] = new SpanTreeNode(_vertexList[end].VertexName,_vertexList[begin].VertexName, edges[i].Weight);count++;}}for (int i = 0; i < parent.Length; i++){if (parent[i] == -1){tree[0] = new SpanTreeNode(_vertexList[i].VertexName, "NULL", 0.0);break;}}return tree;
}
6. 单源最短路径
6.1 定义
设G=(V,E)G=(V,E)G=(V,E)为连通网,vvv为源点,vvv到其余各顶点的最短路径问题即为单源最短路径问题。
6.2 迪杰特撕拉算法
DijkstraDijkstraDijkstra(迪杰特斯拉)算法(按路径长度递增顺序构造的算法):
初始时sss为源点,Ds=0D_s=0Ds=0,Di=+∞(i≠s)D_i= + \infty (i \neq s)Di=+∞(i=s) ,标识sss被访问。
(1)令v=sv=sv=s,Dv=0D_v=0Dv=0(vvv到sss的路径长度)。
(2)依次考察vvv的未被访问的邻接点ω\omegaω,若Dv+weight(v,ω)<DωD_v+weight(v,\omega)<D_\omegaDv+weight(v,ω)<Dω,则改变DωD_\omegaDω的值,使Dω=Dv+weight(v,ω)D_\omega=D_v+weight(v,\omega)Dω=Dv+weight(v,ω)。
(3)在未被访问顶点中选择DvD_vDv最小的顶点vvv,访问vvv。
(4)重复(2)、(3)直至所有顶点都被访问。
例题:
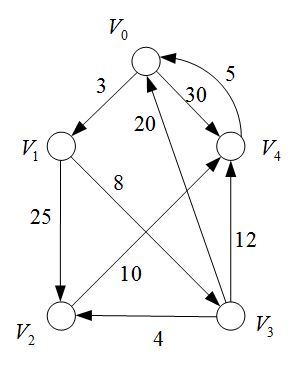
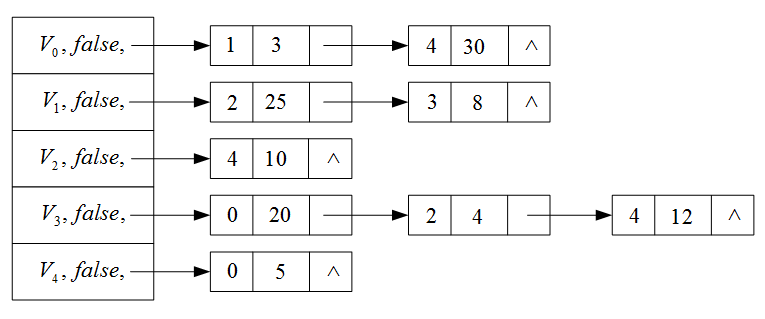

算法实现:
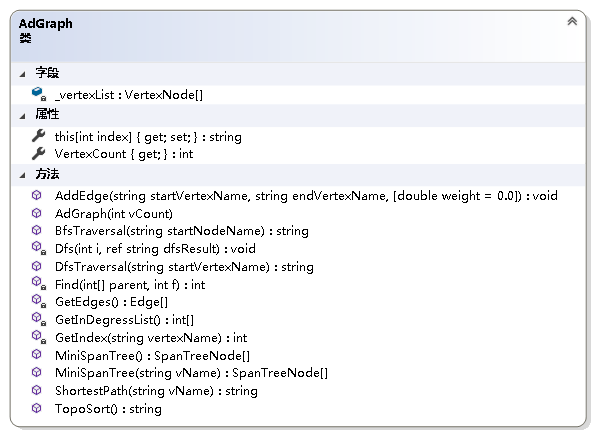
/// <summary>
/// 单源最短路径
/// </summary>
/// <param name="vName">寻找最短路径的源点</param>
/// <returns>源点到各个顶点的最短路径</returns>
public string ShortestPath(string vName)
{int v = GetIndex(vName);if (v == -1){return string.Empty;}string result = string.Empty;double[] dist = new double[VertexCount];string[] path = new string[VertexCount];//初始化for (int i = 0; i < VertexCount; i++){_vertexList[i].Visited = false;dist[i] = double.MaxValue;path[i] = _vertexList[v].VertexName;}dist[v] = 0.0;_vertexList[v].Visited = true;for (int i = 0; i < VertexCount - 1; i++){EdgeNode p = _vertexList[v].FirstNode;while (p != null){if (_vertexList[p.Index].Visited == false&& dist[v] + p.Weight < dist[p.Index]){dist[p.Index] = dist[v] + p.Weight;path[p.Index] = path[v] + " ->" + _vertexList[p.Index].VertexName;}p = p.Next;}double min = double.MaxValue;for (int j = 0; j < VertexCount; j++){if (_vertexList[j].Visited == false && dist[j] < min){min = dist[j];v = j;}}_vertexList[v].Visited = true;}for (int i = 0; i < VertexCount; i++){result += path[i] + ":" + dist[i] + "\n";}return result;
}
7. 连通分量
例题:
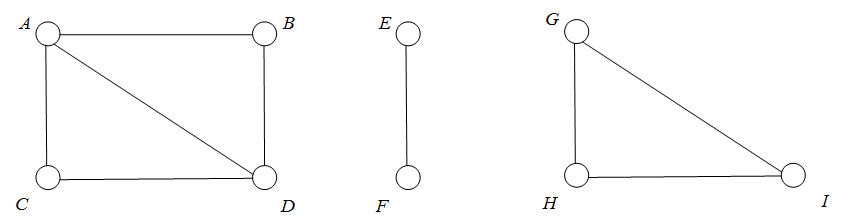
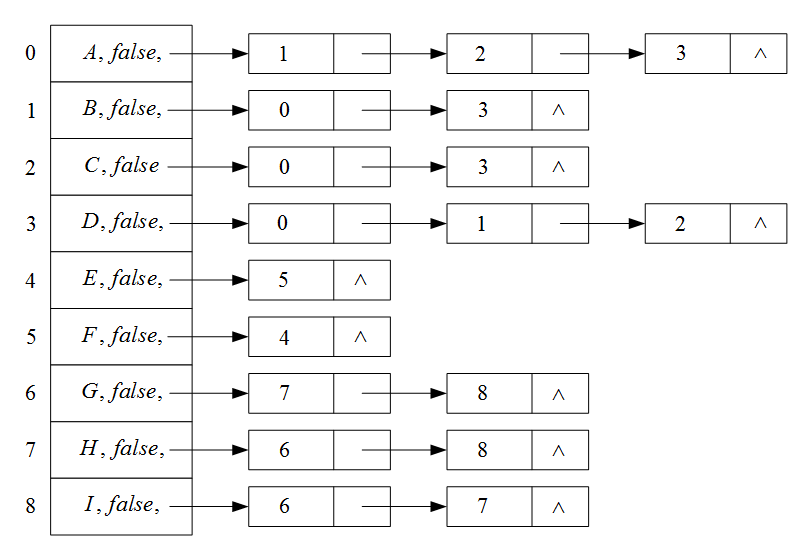
可利用深度优先搜索,求非连通图的连通分量。
第一个:A,B,D,C;第二个:E,F;第三个:G,H,I
算法实现:
/// <summary>
/// 得到连通分量
/// </summary>
/// <returns>连通分量</returns>
public string ConnectedComponent()
{string result;SLinkList<string> lst = new SLinkList<string>();for (int i = 0; i < VertexCount; i++)_vertexList[i].Visited = false;for (int i = 0; i < VertexCount; i++){if (_vertexList[i].Visited == false){result = string.Empty;//利用深度优先搜索求非连通图的连通分量Dfs(i, ref result);lst.InsertAtRear(result);}}result = string.Empty;for (int i = 0; i < lst.Length; i++){result += "第" + i + "个连通分量为:\n" + lst[i];}return result;
}
8. 练习
根据要求完成程序代码:
给定纽约市附近的一幅简单地图,图中的顶点为城市,无向边代表两个城市的连通关系,边上的权为两城市之间的距离。
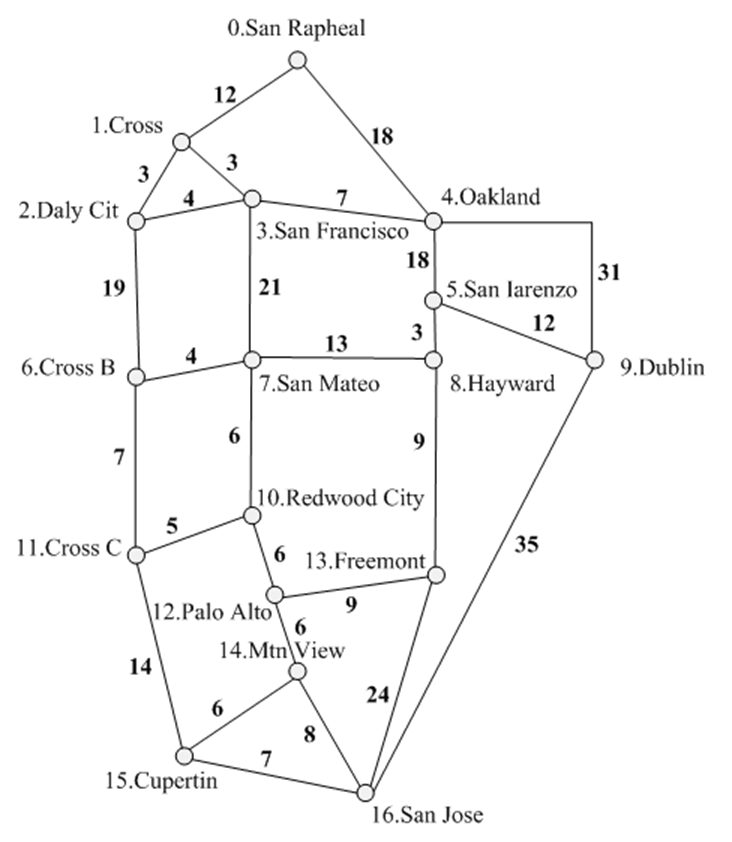
(1)对该图进行深度优先和广度优先搜索,并输出搜索序列(图的搜索问题)。
(2)在分析这张图后可以发现,任一对城市都是连通的。
第一个问题是:要用公路把所有城市连接起来,如何设计可使得工程的总造价最少(最小生成树问题)。
第二个问题是:要开车从一个城市到另外一个城市求其最短距离以及驱车路线(最短路径问题)。
解答:
数据TXT文件:
Source,Target,Weight
San Rapheal,Cross,12
San Rapheal,Oakland,18
Cross,Daly Cit,3
Cross,San Franciso,3
Daly Cit,San Franciso,4
Daly Cit,Cross B,19
San Franciso,Oakland,7
San Franciso,San Mateo,21
Oakland,San Iarenzo,18
Oakland,Dublin,31
San Iarenzo,Hayward,3
San Iarenzo,Dublin,12
Cross B,San Mateo,4
Cross B,Cross C,7
San Mateo,Hayward,13
San Mateo,Redwood City,6
Hayward,Freemont,9
Dublin,San Jose,35
Redwood City,Cross C,5
Redwood City,Palo Alto,6
Cross C,Cupertin,14
Palo Alto,Freemont,9
Palo Alto,Mtn View,6
Freemont,San Jose,24
Mtn View,Cupertin,6
Mtn View,San Jose,8
Cupertin,San Jose,7
深度优先搜索序列:
San Rapheal
Cross
Daly Cit
San Franciso
Oakland
San Iarenzo
Hayward
San Mateo
Cross B
Cross C
Redwood City
Palo Alto
Freemont
San Jose
Dublin
Mtn View
Cupertin
广度优先搜索序列:
San Rapheal
Cross
Oakland
Daly Cit
San Franciso
San Iarenzo
Dublin
Cross B
San Mateo
Hayward
San Jose
Cross C
Redwood City
Freemont
Mtn View
Cupertin
Palo Alto
最小生成树:
(NULL,San Rapheal) Weight:0
(San Rapheal,Cross) Weight:12
(Cross,Daly Cit) Weight:3
(Cross,San Franciso) Weight:3
(San Franciso,Oakland) Weight:7
(Oakland,San Iarenzo) Weight:18
(San Iarenzo,Hayward) Weight:3
(Hayward,Freemont) Weight:9
(Freemont,Palo Alto) Weight:9
(Palo Alto,Redwood City) Weight:6
(Redwood City,Cross C) Weight:5
(Redwood City,San Mateo) Weight:6
(San Mateo,Cross B) Weight:4
(Palo Alto,Mtn View) Weight:6
(Mtn View,Cupertin) Weight:6
(Cupertin,San Jose) Weight:7
(San Iarenzo,Dublin) Weight:12最小生成树权值:116
最短路径:
San Rapheal:0
San Rapheal ->Cross:12
San Rapheal ->Oakland:18
San Rapheal ->Cross ->Daly Cit:15
San Rapheal ->Cross ->San Franciso:15
San Rapheal ->Cross ->Daly Cit ->Cross B:34
San Rapheal ->Cross ->San Franciso ->San Mateo:36
San Rapheal ->Oakland ->San Iarenzo:36
San Rapheal ->Oakland ->San Iarenzo ->Dublin:48
San Rapheal ->Oakland ->San Iarenzo ->Hayward:39
San Rapheal ->Cross ->Daly Cit ->Cross B ->Cross C:41
San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City:42
San Rapheal ->Oakland ->San Iarenzo ->Hayward ->Freemont:48
San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto ->Mtn View ->San Jose:62
San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto:48
San Rapheal ->Cross ->Daly Cit ->Cross B ->Cross C ->Cupertin:55
San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto ->Mtn View:54

相关文章:

云计算安全:技术与应用
云计算安全:技术与应用中国电信网络安全实验室 编著ISBN 978-7-121-14409-72012年1月出版定价:59.00元16开236页宣传语:全面了解云计算安全风险、安全防护手段的佳作!内 容 简 介随着云计算的兴起,安全成为云计算能否顺…

再谈HOST文件
前几天弄了一个关于禁止打开某个网站的文章后,觉得这个HOST文件真的挺有意思的。并且也总是想把自己对它新的理解写下来(也许大家都明白了)以下是HOST文件的内容:# Copyright (c) 1993-1999 Microsoft Corp.## This is a sample H…

PMP®考试是什么机构
项目管理对于很多职场中的人来说是以后要发展的一个方向,随着各职业内卷也越来越严重,pmp认证引起了大家的关注,有朋友问:PMP考试是什么机构?下面我们给大家介绍一下。 PMP考试是什么机构?PMP考试认证在我国大陆地区需要三方机构…
技术图文:03 结构型设计模式(上)
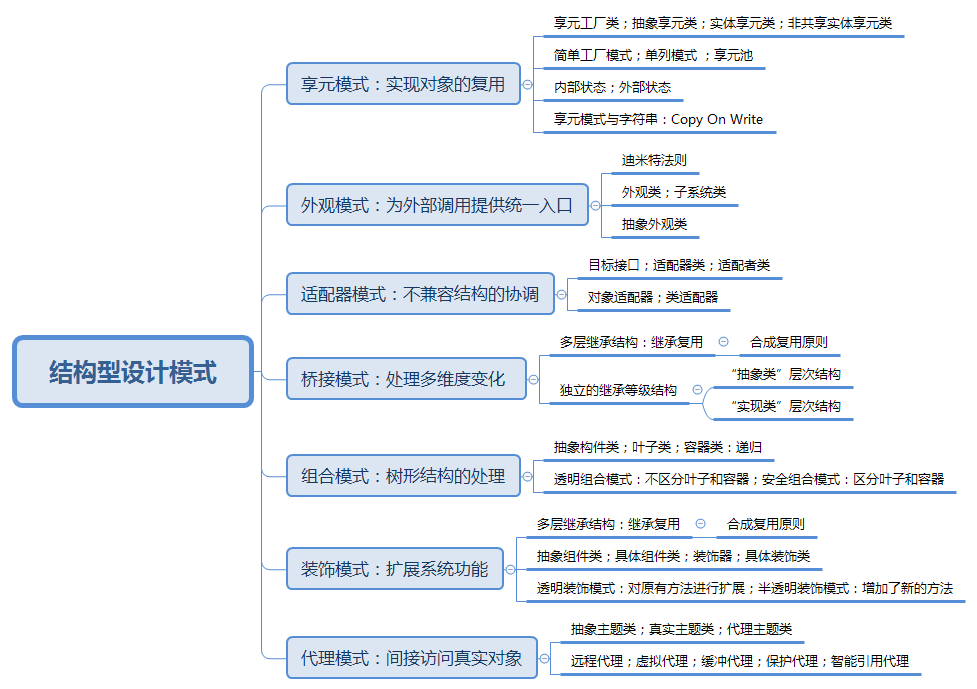
结构型设计模式(上) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 享元模式 – 实现对象的复用 Sunny 软件公司欲开发一个围棋软件,其界面效果如下图所示: 图2 围…

Linux抓包工具tcpdump详解
原文链接 tcpdump是一个用于截取网络分组,并输出分组内容的工具,简单说就是数据包抓包工具。tcpdump凭借强大的功能和灵活的截取策略,使其成为Linux系统下用于网络分析和问题排查的首选工具。 tcpdump提供了源代码,公开了接口&…

学习笔记TF065:TensorFlowOnSpark
2019独角兽企业重金招聘Python工程师标准>>> Hadoop生态大数据系统分为Yam、 HDFS、MapReduce计算框架。TensorFlow分布式相当于MapReduce计算框架,Kubernetes相当于Yam调度系统。TensorFlowOnSpark,利用远程直接内存访问(Remote Direct Memo…

HTML5培训好不好
HTML5培训好不好?这个问题,要看你选择的培训机构,想要学习HTML5技术,靠谱的培训机构非常重要,下面我们就来看看详细的介绍吧。 HTML5培训好不好?从前端开发的基础出发,学习使用HTML,CSS,JavaS…

技术图文:03 结构型设计模式(下)
结构型设计模式(下) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 组合模式 – 树形结构的处理 Sunny 软件公司欲开发一个杀毒(AntiVirus)软件,该软件…

程序员必知8大排序3大查找(三)
前两篇 《程序员必知8大排序3大查找(一)》 《程序员必知8大排序3大查找(二)》 三种查找算法:顺序查找,二分法查找(折半查找),分块查找,散列表(以后谈…
MongoDB给数据库创建用户
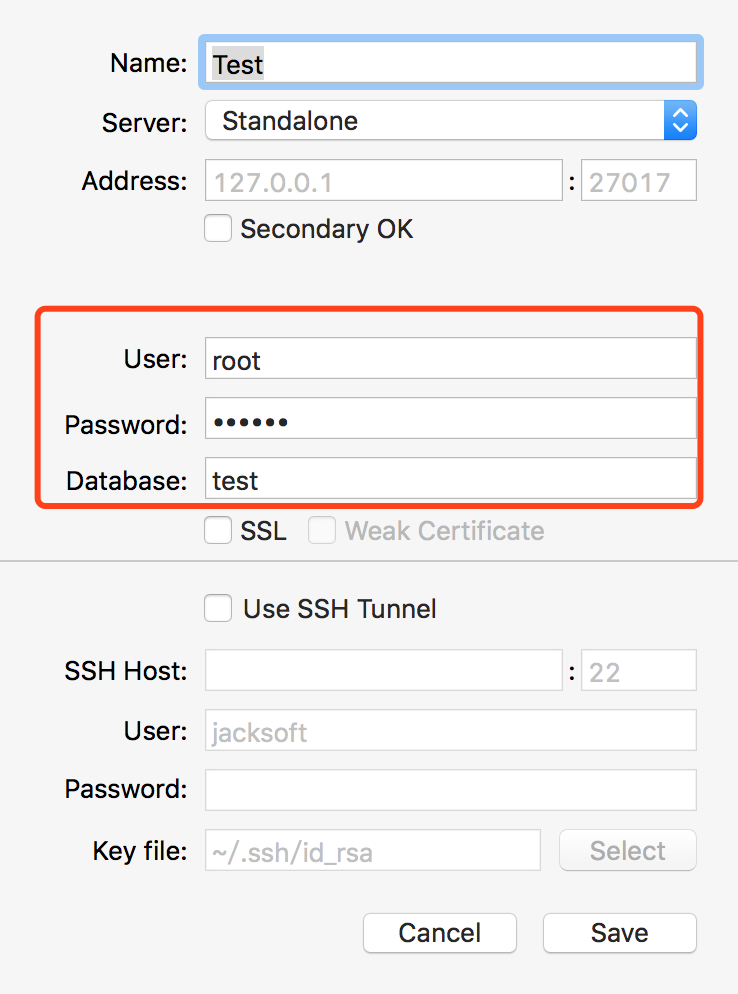
转自http://www.imooc.com/article/18439 一.先以非授权的模式启动MongoDB非授权: linux/Mac : mongod -f /mongodb/etc/mongo.confwindows : mongod --config c:\mongodb\etc\mongo.conf 或者 net start mongodb (前提是mongo安装到了服务里面ÿ…

如何挑选一家好的软件测试培训机构
随着智能时代的发展,我们的手机APP等各种软件都变得越来越复杂化、规模化,软件测试这一步骤是必不可少的,这也造就了这个行业的兴起,越来越多的人想要学习软件测试技术,想要知道如何挑选一家好的软件测试培训机构?来看…

POJ 3177 判决素数个数
时间限制: 1000ms内存限制:65536kB描述输入两个整数X和Y,输出两者之间的素数个数(包括X和Y)。输入两个整数X和Y,X和Y的大小任意。输出输出一个整数,结果可以是0,或大于0的整数。样例输入1 100样例输出25&am…

数据结构与算法:22 精选练习50
精选练习50 马上就要期末考试或者考研了。为了大家复习的方便,我精选了有关数据结构与算法的50道选择题,大家可以抽空练习一下。公众号后台回复“答案”可以获取该50道题目的答案。 01、数据在计算机中的表示称为数据的______。 (A&#x…

极速理解设计模式系列:11.单例模式(Singleton Pattern)
单例模式:确保某一个类只有一个实例,而且自行实例化并向整个系统提供这个实例。这个类称为单例类。 三要点: 一、单例类只能有一个实例 二、单例类必须自行创建自身实例 三、单例类自行向整个系统提供实例 类图: 应用场景…

参加web前端培训要学哪些知识
IT行业,web前端技术是比较吃香的,也是工资待遇非常高的行业之一,如果想要做一名合格的web前端工程师,系统学习是非常重要的,那么参加web前端培训要学哪些知识呢?来看看下面的详细介绍。 参加web前端培训要学哪些知识?…
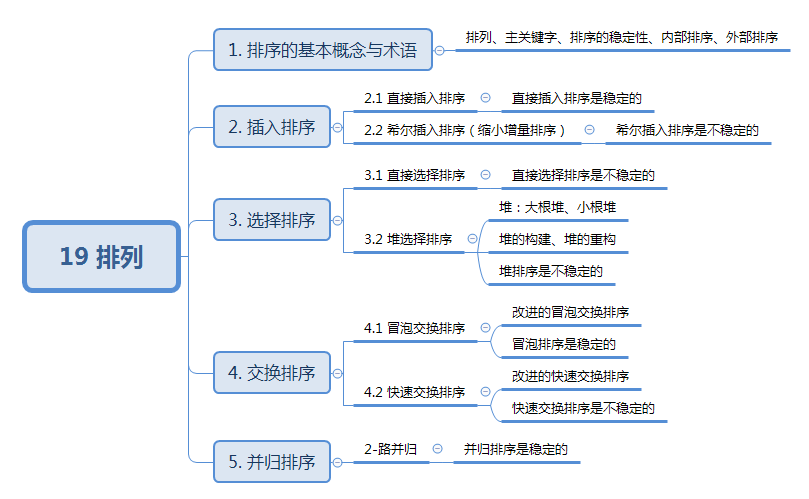
数据结构与算法:19 排序
19 排序 知识结构: 1. 排序的基本概念与术语 假设含有nnn个记录的序列为{r1,r2,⋯,rn}\lbrace r_1,r_2,\cdots,r_n \rbrace{r1,r2,⋯,rn},其相应的关键字分别为{k1,k2,⋯,kn}\lbrace k_1,k_2,\cdots,k_n \rbrace{k1,k2,⋯,kn},…

Objective-C 什么是类
Objective-C 什么是类 转自http://www.189works.com/article-31219-1.html 之前一直做C开发,最近2个多月转 Objective-C, 入门的时候,遇到了很多的困惑。现在过节,正是解决他们的好时机。 主要参考来自http://www.sealiesoftware.…

APP之红点提醒三个阶段
下面这个页面就是我们进入APP后的主界面。客户选项的红点上数字就是显示我们没有查看的客户总数量。 当我们切换到客户这个fragment时,会显示贷款客户数量与保险客户数量。 当我们随便点击入一个选项,假如进入到保险客户的这个activity里面,L…

零基础参加java培训的系统学习路线
零基础想要学习java技术,那么最好的选择就是参加java培训,进行系统的学习,以下就是小编为大家整理的零基础参加java培训的系统学习路线,希望能够帮助到正在学习java技术的零基础同学。 零基础参加java培训的系统学习路线&#…

在ASP.NET中跟踪和恢复大文件下载
在Web应用程序中处理大文件下载的问题一直出了名的困难,因此对于大多数站点来说,如果用户的下载被中断了,它们只能说悲哀降临到用户的身上了。但是我们现在不必这样了,因为你可以使自己的ASP.NET应用程序有能力支持可恢复…

ZeroMQ实例-使用ZeroMQ进行windows与linux之间的通信
1、本文包括 1)在windows下使用ZMQ 2)在windows环境下与Linux环境下进行网络通信 2、在Linux下使用ZMQ 之前写过一篇如何在Linux环境下使用ZMQ的文章 《ZeroMQ实例-使用ZMQ(ZeroMQ)进行局域网内网络通信》,这里就不再赘述。 3、在Windows环境…

线性代数:03 向量空间 -- 基本概念
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点…

如何获得PMP认证证书
pmp证书是一项由美国项目管理协会发起的项目管理专业人士认证证书,它属于国际认证类证书,含金量是非常高的,那么如何获得PMP认证证书呢?来看看下面的详细介绍。 如何获得PMP证书? PMP证书的获取是需要参加PMP考试的。我国自1999年引进PM…

UITextField的详细使用
UItextField通常用于外部数据输入,以实现人机交互。下面以一个简单的登陆界面来讲解UItextField的详细使用。//用来显示“用户名”的labelUILabel* label1 [[UILabelalloc] initWithFrame:CGRectMake(15, 65, 70, 30)];label1.backgroundCol…

06-hibernate注解-一对多单向外键关联
一对多单向外键 1,一方持有多方的集合,一个班级有多个学生(一对多)。 2,OneToMany(cascade{CascadeType.ALL}, fetchFetchType.LAZY ) //级联关系,抓取策略:懒加载。 JoinColumn(name"c…

线性代数:03 向量空间 -- 矩阵的零空间,列空间,线性方程组解的结构
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点…

学Python培训有什么用
Python在近几年的发展非常迅速,在互联网行业Python的薪资也越来越高,不少人开始准备学习Python技术,那么到底学Python培训有什么用呢?来看看下面的详细介绍。 学Python培训有什么用? 学习python可以提高工作效率,使用python&…

SQL压力测试用的语句和相关计数器
将数据库中所有表的所有的内容选一遍: IF object_id(tempdb..#temp) is not null BEGIN DROP TABLE #temp END DECLARE index int DECLARE count int DECLARE schemaname varchar(50) DECLARE tablename varchar(50) set index1 set count(select count(*) from s…

线性代数:04 特征值与特征向量 -- 特征值与特征向量
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍特征值与特征向量的知识,前一章我们介绍了线性变换可以把一个向量映射到另一个…

使用Silverlight2的WebClient下载远程图片
在Silverlight 2之前有一个Downloader对象,开发者一般使用Downloader下载图片和文体文件,这个对象在Silverlight 2中作为了一个特性被集成到WebClient类之中,你可以直接使用WebClient的OpenReadAsync方法加载远程图片的URI,然后使…
