线性代数:03 向量空间 -- 基本概念
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。
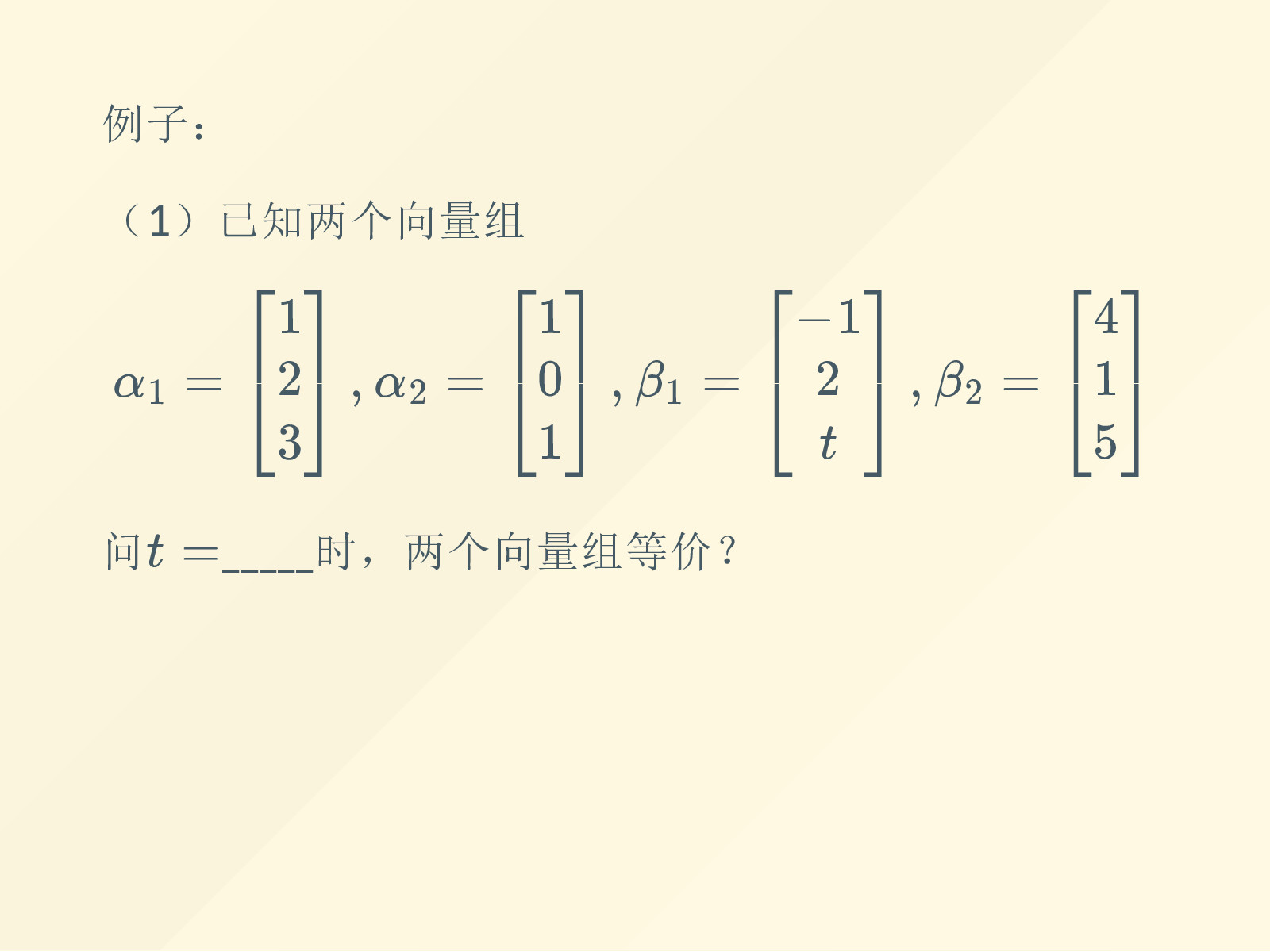
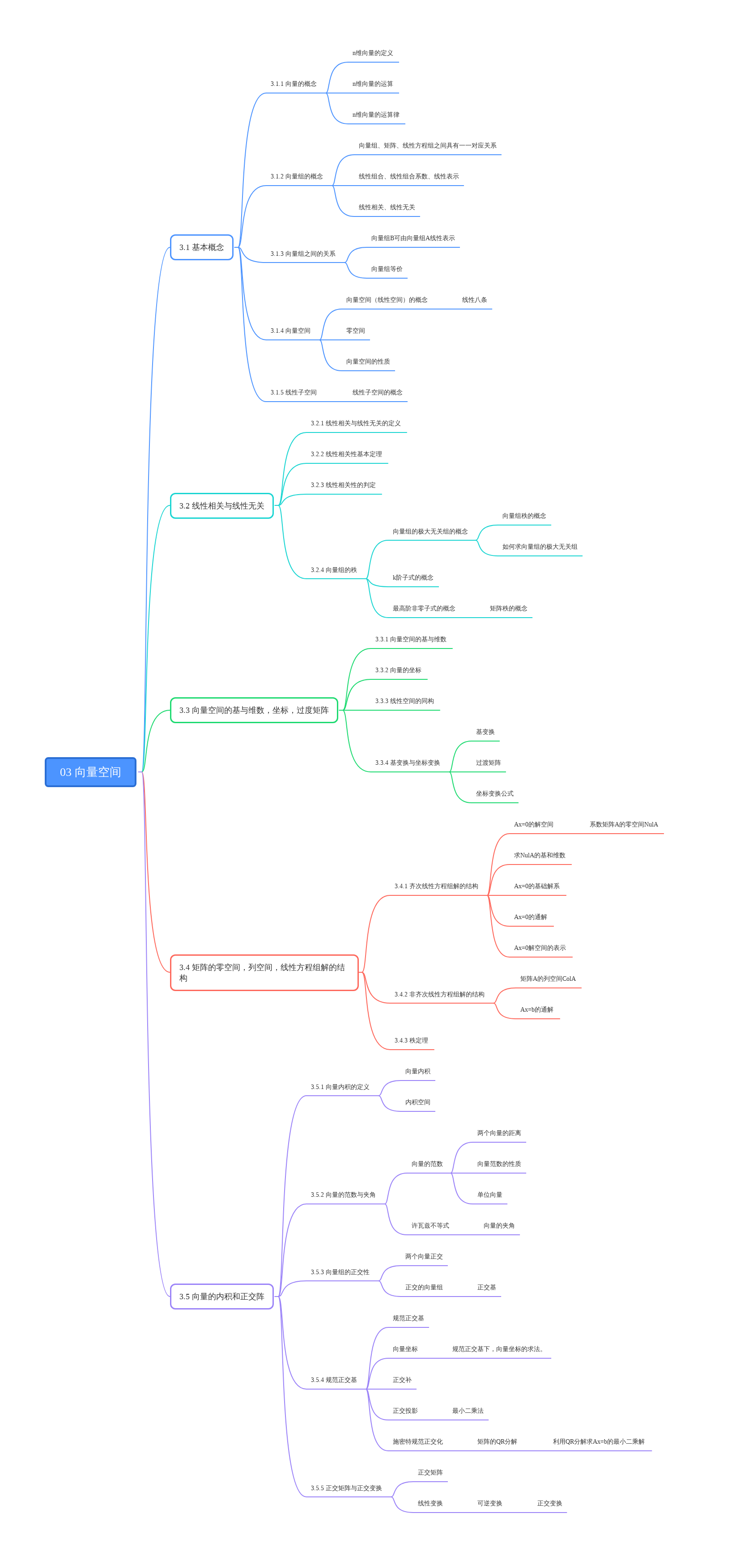
本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点串联起来,比如研究齐次线性方程组的解可以得到线性相关、线性无关、零空间、解空间的基(基础解系)、解空间的维数、秩定理等概念。研究非齐次线性方程组的解可以得到线性组合、线性表示、列空间、一个向量组可由另一个向量组线性表示、两个向量组等价等概念。若一个向量不在矩阵的列空间当中,即这个向量不能由一组向量线性表示,可以通过正交投影定理得到最小二乘解,而QR分解是求最小二乘解的一种有效途径。本章的核心是向量空间的概念,通过向量空间的同构,可以把其它的向量空间同构到RnR^nRn空间,为了表达坐标的方便,我们通常会选择标准正交基,作为该空间的基。本章相对前两章就有一些难度了,希望大家好好复习,把基本概念和方法搞明白。
推荐两个学习线性代数的资源:
1. 麻省理工公开课 Linear Algebra
- https://www.bilibili.com/video/av15463995/
- 相较于国内老师从行列式入手,MIT老师从几何空间的角度,更加直观揭示线代的内核。
2. 线性代数的本质
- https://www.bilibili.com/video/BV1ys411472E
- 通过直观的动画演示来理解线性代数的大部分核心概念。
关注本公众号并回复“资料下载”可以获取MIT线性代数公开课英文教材和中文笔记一份,以方便大家学习。

























相关文章:

如何获得PMP认证证书
pmp证书是一项由美国项目管理协会发起的项目管理专业人士认证证书,它属于国际认证类证书,含金量是非常高的,那么如何获得PMP认证证书呢?来看看下面的详细介绍。 如何获得PMP证书? PMP证书的获取是需要参加PMP考试的。我国自1999年引进PM…

UITextField的详细使用
UItextField通常用于外部数据输入,以实现人机交互。下面以一个简单的登陆界面来讲解UItextField的详细使用。//用来显示“用户名”的labelUILabel* label1 [[UILabelalloc] initWithFrame:CGRectMake(15, 65, 70, 30)];label1.backgroundCol…

06-hibernate注解-一对多单向外键关联
一对多单向外键 1,一方持有多方的集合,一个班级有多个学生(一对多)。 2,OneToMany(cascade{CascadeType.ALL}, fetchFetchType.LAZY ) //级联关系,抓取策略:懒加载。 JoinColumn(name"c…

线性代数:03 向量空间 -- 矩阵的零空间,列空间,线性方程组解的结构
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点…

学Python培训有什么用
Python在近几年的发展非常迅速,在互联网行业Python的薪资也越来越高,不少人开始准备学习Python技术,那么到底学Python培训有什么用呢?来看看下面的详细介绍。 学Python培训有什么用? 学习python可以提高工作效率,使用python&…

SQL压力测试用的语句和相关计数器
将数据库中所有表的所有的内容选一遍: IF object_id(tempdb..#temp) is not null BEGIN DROP TABLE #temp END DECLARE index int DECLARE count int DECLARE schemaname varchar(50) DECLARE tablename varchar(50) set index1 set count(select count(*) from s…

线性代数:04 特征值与特征向量 -- 特征值与特征向量
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍特征值与特征向量的知识,前一章我们介绍了线性变换可以把一个向量映射到另一个…

使用Silverlight2的WebClient下载远程图片
在Silverlight 2之前有一个Downloader对象,开发者一般使用Downloader下载图片和文体文件,这个对象在Silverlight 2中作为了一个特性被集成到WebClient类之中,你可以直接使用WebClient的OpenReadAsync方法加载远程图片的URI,然后使…

学习Web前端需要避免哪些错误
很多初学web前端的同学,在学习web前端的时候都会遇到一些错误,虽然有些错误与某一个具体的行为相关,但有些错误却是所有Web开发人员都需要面对的挑战。下面小编就整理一下学习Web前端需要避免哪些错误,希望能够给同学们带来帮助。…

【2012百度之星/资格赛】H:用户请求中的品牌 [后缀数组]
时间限制:1000ms内存限制:65536kB描述馅饼同学是一个在百度工作,做用户请求(query)分析的同学,他在用户请求中经常会遇到一些很奇葩的词汇。在比方说“johnsonjohnson”、“duckduck”,这些词汇虽然看起来是一些词汇的…

实战:使用Telnet排除网络故障
使用Telnet排除网络故障 如果员工告诉你,他的计算机不能访问网站。你需要断定是他的计算机系统出了问题还是IE浏览器中了恶意插件,或者是网络层面的问题。 如图2-108所示,通过Telnet 服务器的某个端口,就能断定是否访问该服务器的…

线性代数:04 特征值与特征向量 -- 矩阵的相似对角化
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍特征值与特征向量的知识,前一章我们介绍了线性变换可以把一个向量映射到另一个…

UI设计培训完之后可以去哪些公司工作
UI设计培训完之后可以去哪些公司工作?这是目前很多学习UI设计或者准备学习UI设计的同学比较关注的一个问题,虽然都知道UI设计的发展前景不错,但是具体学完之后该去哪里工作大家却比较迷茫,来看看下面的详细介绍吧。 UI设计培训完之后可以去哪…
Tomcat详解(下)
配置监听端口 1、编辑配置文件 1234[rootplinuxos ~]# vim /usr/local/tomcat/conf/server.xml <Connector port"80" protocol"HTTP/1.1" ##改成80端口 connectionTimeout"20000" redirectPort"8443" /> 2、重启服务 123456…

线性代数:05 实对称矩阵与二次型
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章是特征值与特征向量知识的延续,根据谱定理可知实对称矩阵可以正交对角化,对…

HDU 2717 Catch That Cow(BFS)
题目链接 好裸,BFS。杭电多组。。2A。。 1 #include <stdio.h>2 #include <string.h>3 int p[100001],o[100001];4 int main()5 {6 int n,k,i,j,start0,end0,num0;7 while(scanf("%d%d",&n,&k)!EOF)8 {9 memset(…

参加web前端培训需要注意什么
web前端在互联网行业的就业形势是非常良好的,是很多人进入到互联网行业的一个首要选择,要想学会web前端技术,一定要参加系统的培训,那么参加web前端培训需要注意什么呢? 参加web前端培训需要注意什么? 一、选择一家靠谱的培训机…

NIO - Scatter/Gather
1.Scatter 从一个Channel读取的信息分散到N个缓冲区中(Buufer). 2.Gather 将N个Buffer里面内容按照顺序发送到一个Channel. Scatter/Gather功能是通道(Channel)提供的 并不是Buffer, Scatter/Gather相关接口 类图 ReadableByteChannel WritableByteChannel 接口提供…

android:themes.xml
按 CtrlC 复制代码按 CtrlC 复制代码本文转自 OldHawk 博客园博客,原文链接:http://www.cnblogs.com/taobataoma/p/3761520.html,如需转载请自行联系原作者

参考答案:01 线性方程组
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 从本章开始,我们一起来学习线性代数的有关知识,线性代数的应用之一就是求解复杂方程问题。所以,我们首先从高中时期利用高斯消元法求解线性方程组谈起,发现可以利…

Java培训都学什么
java行业的快速发展,引起了很多人的关注,越来越多的人选择报java培训机构学习java技术,那么Java培训都学什么呢?零基础的同学是否能学会呢?来看看下面的详细介绍。 Java培训都学什么?主要分为以下几个阶段: 第一阶段࿱…

网站架构之统一数据服务平台技术
一、论坛背景 新一代网站架构的使命,敏捷,开发,体验。 敏捷:业务快速增长,每天都要上线大量的小需求,应用系统日益膨胀,耦合恶化,架构越来越复杂,带来更高的开发成本。如何保持业务开发敏捷性? 开放:Faceb…

Oracle 变量绑定与变量窥视合集系列二
二 用示例演示一次硬分析(hard parse)和一次软分析(soft parse),以及一次更软的分析(softer soft parse),并对给出演示结果 我们先看一个硬解析和软解析关系测试,什么时候硬解析,什么…

参考答案:02 矩阵及其运算
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 本章主要介绍有关矩阵的知识,主要包括矩阵的基本运算(加法、数乘、乘法、乘幂、迹、转置),其中乘法最为重要,在计算机图形学中具有大量的应用。如果矩…
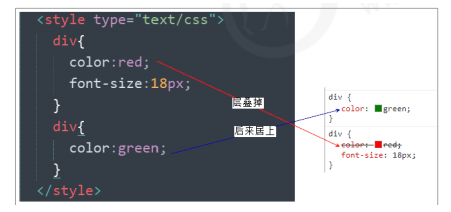
web前端培训:本期教程CSS 三大特性
CSS 有三个非常重要的三个特性:层叠性、继承性、优先级: 1. 层叠性 相同选择器给设置相同的样式,此时一个样式就会覆盖(层叠)另一个冲突的样式。层叠性主要解决样式冲突的问题。 层叠性原则: 样式冲突,遵循的原则是就近…
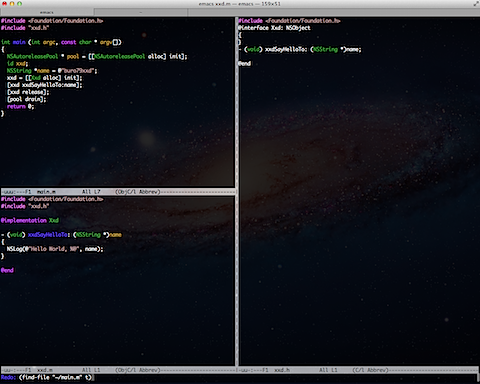
如何在Terminal命令行模式下运行Objective-C
一般Objective-C的代码都在Xcode中调试,今天实验了下如何在命令行模式下运行,还是比较简单的,记录分享一下。 File: xxd.h #include <Foundation/Foundation.h> interface Xxd: NSObject { } - (void) xxdSayHelloTo: (NSString *)name…

人工智能时代,程序员要不要精通算法?
1.如何入门算法?需要学习哪些基础知识,请分享你的经验与建议。 入门算法其实很简单,拿生活中的很多现实问题来解决就可以了。比如商场打折问题(是打折划算还是满减划算),百钱买百鸡、猴子分桃、鸡兔同笼等有…

参考答案:03 向量空间
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点串联起来,比如研究齐次线性方程组的解可以得到线性相关、线性无关、零空间、解空间的基&#…

Java3大框架的学习都是什么
java是互联网行业的第一编程语言,相信大家都已经有了解了,事实也确实如此,java还是世界第一编程语言,在java培训学习的过程中,框架是程序员们必学的知识点,而且是十分重要的应用,Spring、Struts…

百万数据修改索引,百万数据修改主键
当百万数据时,如果修改主键,那么会自动重建索引,所以操作会非常慢,经常会超时,错误提示类似:超时时间已到。在操作完成之前超时时间已过或服务器未响应解决方案:不要采用手动添加主键或者索引&a…
