线性代数:05 实对称矩阵与二次型
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。
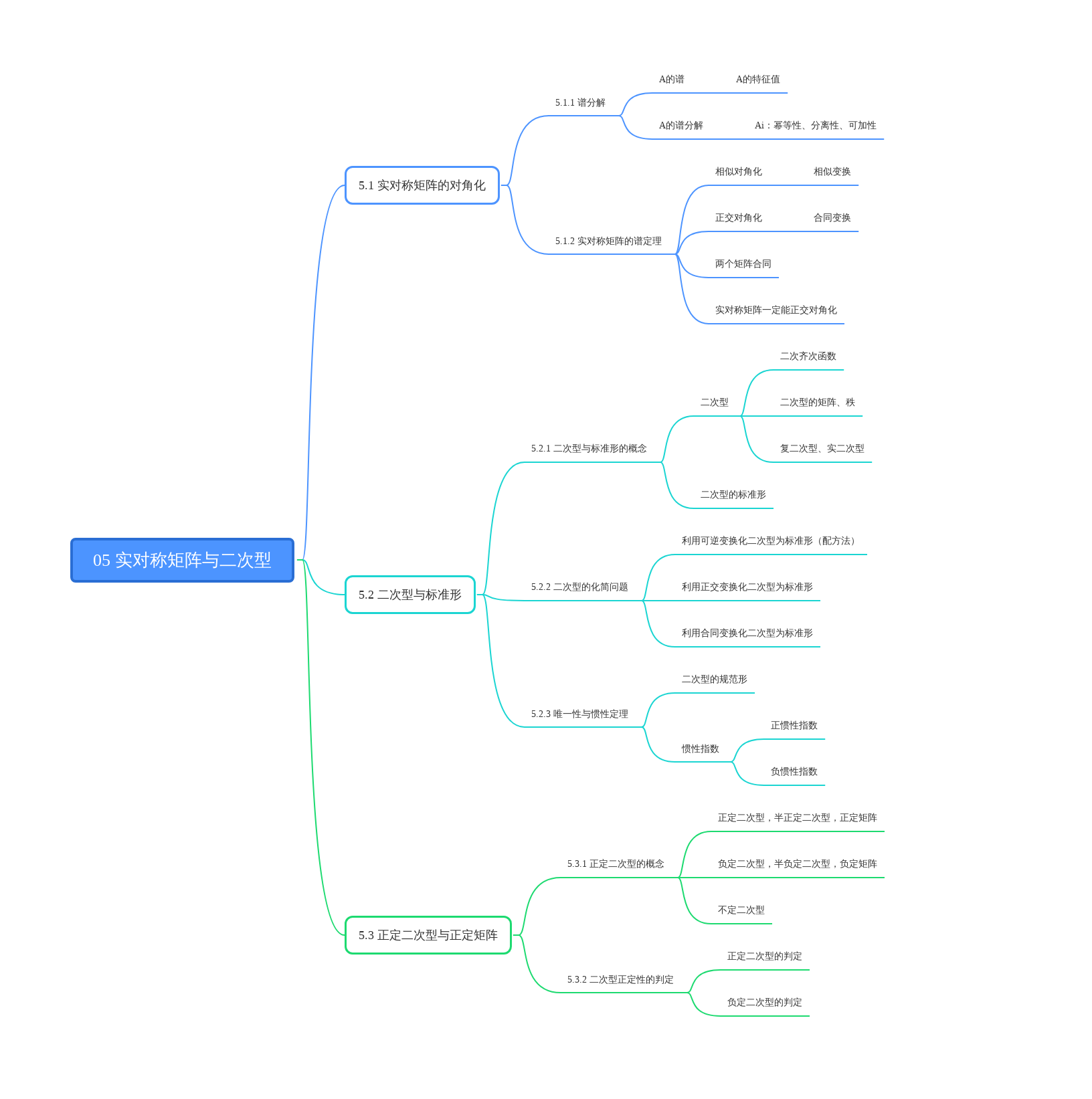
本章是特征值与特征向量知识的延续,根据谱定理可知实对称矩阵可以正交对角化,对角阵为其特征值,正交矩阵为其两两正交的单位特征向量。除此之外,还介绍了二次型,标准形,规范形的知识。二次型的化简问题是本章的核心,我们即可以通过配方法做可逆变换化二次型为标准形,又可以通过正交法做正交变换化二次型为标准形,还可以通过合同法做合同变换化二次型为标准形。由于二次型的标准形不唯一,所以我们去寻找这些标准形的共性,得到了惯性指数、正惯性指数、负惯性指数这些概念,以及惯性定理,发现规范形是唯一的。最后介绍了最特殊的二次型,即正定二次型,其对应的矩阵为正定矩阵。以及正定矩阵的判定定理。本章相对前一章就简单很多了,希望大家好好复习,把基本概念和方法搞明白。
推荐两个学习线性代数的资源:
1. 麻省理工公开课 Linear Algebra
- https://www.bilibili.com/video/av15463995/
- 相较于国内老师从行列式入手,MIT老师从几何空间的角度,更加直观揭示线代的内核。
2. 线性代数的本质
- https://www.bilibili.com/video/BV1ys411472E
- 通过直观的动画演示来理解线性代数的大部分核心概念。
关注本公众号并回复 资料下载 可以获取MIT线性代数公开课英文教材和中文笔记一份,以方便大家学习。










































相关文章:

HDU 2717 Catch That Cow(BFS)
题目链接 好裸,BFS。杭电多组。。2A。。 1 #include <stdio.h>2 #include <string.h>3 int p[100001],o[100001];4 int main()5 {6 int n,k,i,j,start0,end0,num0;7 while(scanf("%d%d",&n,&k)!EOF)8 {9 memset(…

参加web前端培训需要注意什么
web前端在互联网行业的就业形势是非常良好的,是很多人进入到互联网行业的一个首要选择,要想学会web前端技术,一定要参加系统的培训,那么参加web前端培训需要注意什么呢? 参加web前端培训需要注意什么? 一、选择一家靠谱的培训机…

NIO - Scatter/Gather
1.Scatter 从一个Channel读取的信息分散到N个缓冲区中(Buufer). 2.Gather 将N个Buffer里面内容按照顺序发送到一个Channel. Scatter/Gather功能是通道(Channel)提供的 并不是Buffer, Scatter/Gather相关接口 类图 ReadableByteChannel WritableByteChannel 接口提供…

android:themes.xml
按 CtrlC 复制代码按 CtrlC 复制代码本文转自 OldHawk 博客园博客,原文链接:http://www.cnblogs.com/taobataoma/p/3761520.html,如需转载请自行联系原作者

参考答案:01 线性方程组
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 从本章开始,我们一起来学习线性代数的有关知识,线性代数的应用之一就是求解复杂方程问题。所以,我们首先从高中时期利用高斯消元法求解线性方程组谈起,发现可以利…

Java培训都学什么
java行业的快速发展,引起了很多人的关注,越来越多的人选择报java培训机构学习java技术,那么Java培训都学什么呢?零基础的同学是否能学会呢?来看看下面的详细介绍。 Java培训都学什么?主要分为以下几个阶段: 第一阶段࿱…

网站架构之统一数据服务平台技术
一、论坛背景 新一代网站架构的使命,敏捷,开发,体验。 敏捷:业务快速增长,每天都要上线大量的小需求,应用系统日益膨胀,耦合恶化,架构越来越复杂,带来更高的开发成本。如何保持业务开发敏捷性? 开放:Faceb…

Oracle 变量绑定与变量窥视合集系列二
二 用示例演示一次硬分析(hard parse)和一次软分析(soft parse),以及一次更软的分析(softer soft parse),并对给出演示结果 我们先看一个硬解析和软解析关系测试,什么时候硬解析,什么…

参考答案:02 矩阵及其运算
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 本章主要介绍有关矩阵的知识,主要包括矩阵的基本运算(加法、数乘、乘法、乘幂、迹、转置),其中乘法最为重要,在计算机图形学中具有大量的应用。如果矩…
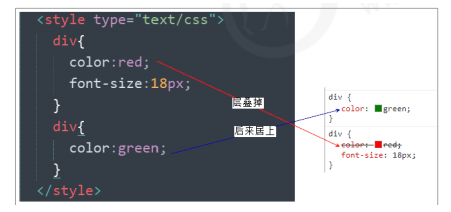
web前端培训:本期教程CSS 三大特性
CSS 有三个非常重要的三个特性:层叠性、继承性、优先级: 1. 层叠性 相同选择器给设置相同的样式,此时一个样式就会覆盖(层叠)另一个冲突的样式。层叠性主要解决样式冲突的问题。 层叠性原则: 样式冲突,遵循的原则是就近…
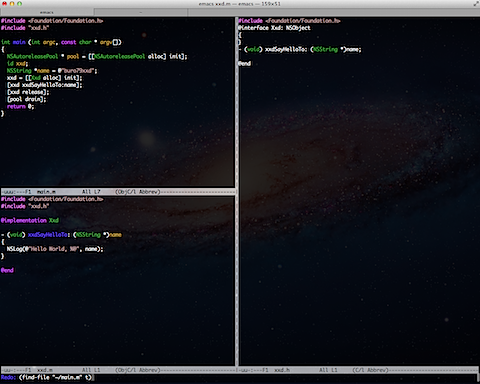
如何在Terminal命令行模式下运行Objective-C
一般Objective-C的代码都在Xcode中调试,今天实验了下如何在命令行模式下运行,还是比较简单的,记录分享一下。 File: xxd.h #include <Foundation/Foundation.h> interface Xxd: NSObject { } - (void) xxdSayHelloTo: (NSString *)name…

人工智能时代,程序员要不要精通算法?
1.如何入门算法?需要学习哪些基础知识,请分享你的经验与建议。 入门算法其实很简单,拿生活中的很多现实问题来解决就可以了。比如商场打折问题(是打折划算还是满减划算),百钱买百鸡、猴子分桃、鸡兔同笼等有…

参考答案:03 向量空间
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点串联起来,比如研究齐次线性方程组的解可以得到线性相关、线性无关、零空间、解空间的基&#…

Java3大框架的学习都是什么
java是互联网行业的第一编程语言,相信大家都已经有了解了,事实也确实如此,java还是世界第一编程语言,在java培训学习的过程中,框架是程序员们必学的知识点,而且是十分重要的应用,Spring、Struts…

百万数据修改索引,百万数据修改主键
当百万数据时,如果修改主键,那么会自动重建索引,所以操作会非常慢,经常会超时,错误提示类似:超时时间已到。在操作完成之前超时时间已过或服务器未响应解决方案:不要采用手动添加主键或者索引&a…

参考答案:05 实对称矩阵与二次型
本篇图文为《线性代数及其应用》这本教材对应习题册的参考答案。 本章是特征值与特征向量知识的延续,根据谱定理可知实对称矩阵可以正交对角化,对角阵为其特征值,正交矩阵为其两两正交的单位特征向量。除此之外,还介绍了二次型&a…

会话保持之iRule脚本
拓扑 思路: Web上的请求,很大程度上需要在后端一台服务器上运行,而不能将请求1,与请求2分别在不同的真实机上。所以,就需要使用会话保持技术了。F5的会话保持有内置的,如简单会话保持,就是根据客户端ip地址而更新会话表…

pmp考试标准有哪些?
pmp认证在互联网行业近几年广受企业的关注,越来越多的职场人员都想参加pmp培训认证,那么pmp考试标准有哪些?学历标准又是怎样的?来看看下面详细的介绍吧。 pmp考试标准有哪些?首先报名参加PMP培训认证对文凭并没有规定,无论文凭好坏&#…

【经验】【ORACLE】从字符串中截取其中的数字
方法一:如果Oracle版本不是太低的话,使用 正则表达式函数 REGEXP_SUBSTR 处理。 REGEXP_SUBSTR有5个参数,分别是: 第一个是输入的字符串 第二个是正则表达式 第三个是标识从第几个字符开始正则表达式匹配。(默认为1&am…

为什么结构主机和全局编录服务器不能放在同一个域控制器上?
”注意:结构主机 (IM) 角色应由非全局编录 (GC) 服务器的域控制器担任。如果结构主机在全局编录服务器上运行,它将会停止更新对象信息,原因是它只包含对它所拥有的对象的引用。“我有个疑问:在装域控制的时候,第一个装…

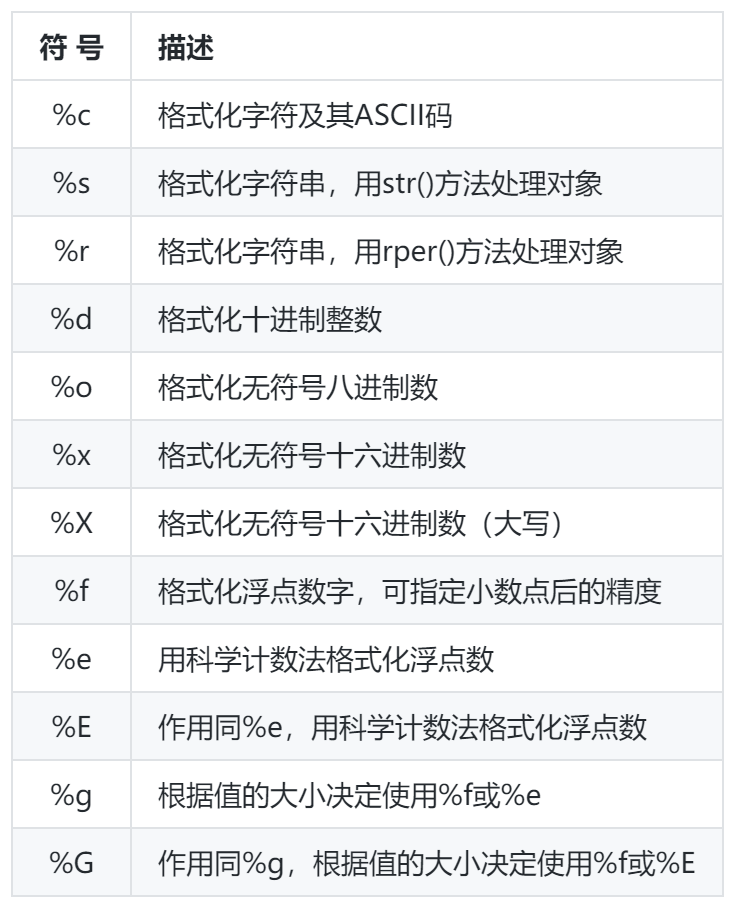
题目 1083:【蓝桥杯】【入门题】Hello, world!
题目 1083:Hello, world! 蓝桥杯刷题群已成立,微信后台回复【蓝桥杯】,即可进入。 如果加入了之前的社群不需要重复加入。 时间限制: 1Sec 内存限制: 64MB 1. 题目描述 这是要测试的第一个问题。由于我们都知道ASCII码,因此您的…

软件测试培训教程:pytest与unittest区别
在软件测试培训教程中,会讲到关于pytest与unittest区别,那么本期教程小编就为大家详细的介绍一下pytest与unittest区别有哪些? pytest与unittest区别: 一、用例编写规则 1.unittest提供了testcases、testsuites、testfixtures、testrunner相…

NA-NP-IE系列实验36:扩展ACL
实验36:扩展ACL1.实验目的 通过本实验可以掌握:(1)定义扩展ACL(2)应用扩展ACL(3)扩展ACL 调试2.拓扑结构 实验拓扑如图所示。3.实验步骤 注:本实验要求不允许1.1.1.1 所在…
题目 1470:【蓝桥杯】【入门题】【基础练习VIP】时间转换
题目 1470:时间转换 蓝桥杯刷题群已成立,微信后台回复【蓝桥杯】,即可进入。 如果加入了之前的社群不需要重复加入。 时间限制: 1Sec 内存限制: 128MB 1. 题目描述 给定一个以秒为单位的时间t,要求用 “< H> :< M> …

Android如何防止apk程序被反编译
作为Android应用开发者,不得不面对一个尴尬的局面,就是自己辛辛苦苦开发的应用可以被别人很轻易的就反编译出来。Google似乎也发现了这个问题,从SDK2.3开始我们可以看到在android-sdk-windows\tools\下面多了一个proguard文件夹 proguard是一…
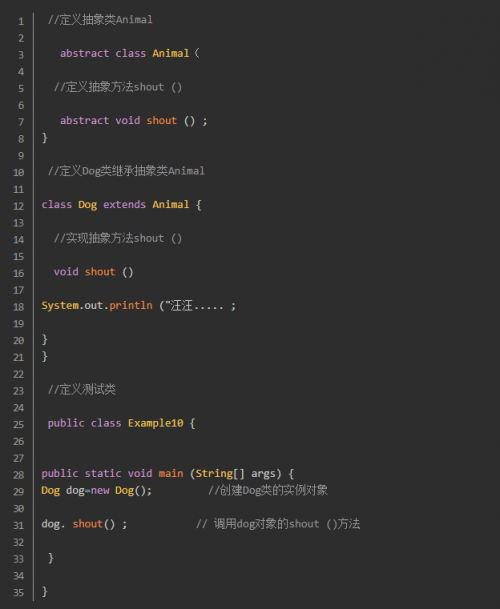
java培训:什么是抽象类?怎么定义?
什么是抽象类?怎么定义?这是属于java技术里面的一个知识点,本期教程就是围绕这个问题做的相关介绍,当定义一个类时,常常需要定义一些成员方法描述类的行为特征,但有时这些方法的实现方式是无法确定的。例如,在定义An…

题目 1093:【蓝桥杯】【入门题】字符逆序
题目 1093:字符逆序 蓝桥杯刷题群已成立,微信后台回复【蓝桥杯】,即可进入。 如果加入了之前的社群不需要重复加入。 时间限制: 1Sec 内存限制: 64MB 1. 题目描述 将一个字符串str的内容颠倒过来,并输出。str的长度不超过100个字…

一款腾讯UED设计的提示插件(使用教程)
这是一款腾讯UED设计的提示插件,看着肯定很眼熟吧,闲话不多说,直接上demo吧。 显示 ZENG.msgbox.show(提示信息,图标类型);隐藏: ZENG.msgbox._hide();几秒后自动隐藏: ZENG.msgbox.show(提示信息,图标类型,显示时长);…

互联网企业的移动布局
转载于:https://www.cnblogs.com/deve/archive/2012/06/13/2568988.html

女生学软件测试有哪些优势
对于软件测试这个岗位,相信大家都有听说过,最近几年,越来越多的女性加入到互联网技术行业,选择最多的岗位就是软件测试,那么到底女生学软件测试有哪些优势呢?来看看下面的详细介绍。 女生学软件测试有哪些优势?首先咱…
