19 排序

知识结构：

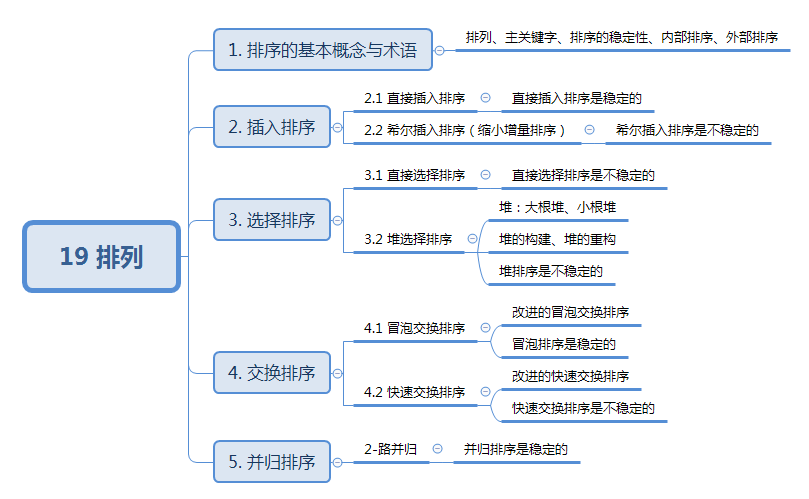
1. 排序的基本概念与术语

假设含有$n$个记录的序列为$\{r_1,r_2,\cdots ,r_n\}$，其相应的关键字分别为$\{k_1,k_2,\cdots ,k_n\}$，需确定 的一种排列$1,2,\cdots ,n$，使其相应的关键字满足$k_{p_1}\le k_{p_2}\le \cdots \le k_{p_n}$的关系，即使得序列成为一个按关键字有序的序列 ，这个样的操作就称为 排列。

能唯一标识某一记录的关键字称为 主关键字。

假设$k_i=k_j(1\le i\le n,1\le j\le n,i\ne j)$，且在排序前的序列中$r_i$领先于$r_j$（即$i<j$ ）。如果排序后$r_i$仍领先于$r_j$，则称所用的排序方法是稳定的；反之，若可能使得排序后的序列中$r_j$领先于$r_i$，则称所用的排序方法是不稳定的。

例如：

• 待排序序列：$20,30,\overline{20}$
• 稳定的排序结果：$20,\overline{20},30$
• 不稳定的排序结果：$\overline{20},20,30$

内部排序：排序过程都在内存中进行的排序。

外部排序：排序过程需要在内存和外存之间不断交换数据的排序。

根据排序过程中借助的主要操作，我们把内排序分为：插入排序、选择排序、交换排序和并归排序。可以说，这些都是比较成熟的排序技术，已经被广泛地应用于许许多多的程序语言或数据库当中，甚至它们都已经封装了关于排序算法的实现代码。因此，我们学习这些排序算法的目的不是为了去现实排序算法，而是通过学习来提高我们编写算法的能力，以便于去解决更多复杂和灵活的应用性问题。

2. 插入排序

2.1 直接插入排序

将一个记录插入到已经排好序的有序表中，从而得到一个新的记录增1的有序表。

即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

排序过程：

$init0\to [45],\overline{34},78,12,34,32,29,64$

$step1\to [\overline{34},45],78,12,34,32,29,64$

$step2\to [\overline{34},45,78],12,34,32,29,64$

$step3\to [12,\overline{34},45,78],34,32,29,64$

$step4\to [12,\overline{34},34,45,78],32,29,64$

$step5\to [12,32,\overline{34},34,45,78],29,64$

$step6\to [12,29,32,\overline{34},34,45,78],64$

$result\to [12,29,32,\overline{34},34,45,64,78]$

程序代码：

/// <summary>
/// 直接插入排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam>
/// <param name="array">需要排序的记录集合</param>
public static void StraightInsertSort<T>(T[] array) where T : IComparable<T>
{for (int i = 1; i < array.Length; i++){int j = i - 1;T current = array[i];while (j >= 0 && array[j].CompareTo(current) > 0){array[j + 1] = array[j];j--;}array[j + 1] = current;}
}

如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面，所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以直接插入排序是稳定的。

2.2 希尔插入排序

希尔排序是1959年由D.L.Shell提出来的，相对直接插入排序有较大的改进。希尔插入排序又叫做缩小增量排序。

直接插入排序的效率在某些时候是很高的，比如我们的记录本身就是基本有序的，我们只需要少量的插入操作，就可以完成整个记录集的排序工作，此时直接插入排序很高效。还有就是记录数比较少时，直接插入的优势也比较明显。可问题在于，两个条件本身就过于苛刻，现实中记录少或者基本有序都属于特殊情况。

不过别着急，有条件当然是好，条件不存在，我们创造条件也是可以去做的。于是科学家希尔研究出了一种排序方法，对直接插入排序改进后可以增加效率。

思想：按待排序列下标的一定增量分组（如：增量序列$t_1,t_2,\cdots ,t_k$，其中$t_i>t_j$，$t_k=1$），将整个待排序列分割成若干子序列，分别进行直接插入排序，随着增量逐渐减少，所分组包含的记录越来越多，到增量值减至1时，整个记录集被分成一组（这时待排序列“基本有序”），再对全体记录进行直接插入排序，算法终止（对待排序列进行了$k$趟直接插入排序）。

我所理解Shell Insertion Sort最牛的地方是，让排序算法能够并行化。

希尔插入排序增量的取法：

$delta1=\left[\frac{n}{2}\right]=\left[\frac{10}{2}\right]=5$

$delta2=\left[\frac{delta1}{2}\right]=\left[\frac{5}{2}\right]=2$

$delta3=\left[\frac{delta2}{2}\right]=\left[\frac{2}{2}\right]=1$

即：先将要排序的一组记录按某个增量$delta$（$\left[\frac{n}{2}\right]$ ，$n$为要排序数的个数）分成若干组子序列，每组中记录的下标相差$delta$。对每组中全部元素进行直接插入排序，然后在用一个较小的增量（$\left[\frac{delta}{2}\right]$ ）对它进行分组，在每组中再进行直接插入排序。继续不断缩小增量直至为1，最后使用直接插入排序完成排序。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

排序过程：

$d=4\to 45,\overline{34},78,12,34,32,29,64$

$d=2\to 34,32,29,12,45,\overline{34},78,64$

$d=1\to 29,12,34,32,45,\overline{34},78,64$

$result\to 12,29,32,34,\overline{34},45,64,78$

程序代码：

private static void Shell<T>(int delta, T[] array) where T : IComparable<T>
{//带增量的直接插入排序for (int i = delta; i < array.Length; i++){int j = i - delta;T current = array[i];while (j >= 0 && array[j].CompareTo(current) > 0){array[j + delta] = array[j];j = j - delta;}array[j + delta] = current;}
}/// <summary>
/// 希尔插入排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam>
/// <param name="array">需要排序的记录集合</param>
public static void ShellInsertSort<T>(T[] array) where T : IComparable<T>
{for (int delta = array.Length/2; delta > 0; delta = delta/2){Shell(delta, array);}
}

希尔插入排序时效分析很难，关键码的比较次数与记录移动次数依赖于增量因子序列$delta$的选取。目前还没有人给出选取最好的增量因子序列的方法。希尔插入排序方法是一个不稳定的排序方法。

3. 选择排序

3.1 直接选择排序

思想：每一趟在$n-i(i=0,1,\cdots ,n-1)$个记录中选取关键字最小的记录作为有序序列中第$i$个记录。（在要排列的一组数中，选出最小的一个数与第1个位置的数交换；然后在剩下的数当中再找最小的与第2个位置的数交换，依次类推，直到第$n-1$个元素和第$n$个元素比较为止。）

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

排序过程：

$i=0\to 12,\overline{34},78,45,34,32,29,64$

$i=1\to 12,29,78,45,34,32,\overline{34},64$

$i=2\to 12,29,32,45,34,78,\overline{34},64$

$i=3\to 12,29,32,34,45,78,\overline{34},64$

$i=4\to 12,29,32,34,\overline{34},78,45,64$

$i=5\to 12,29,32,34,\overline{34},45,78,64$

$i=6\to 12,29,32,34,\overline{34},45,64,78$

程序代码：

/// <summary>
/// 直接选择排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam>
/// <param name="array">需要排序的记录集合</param>
public static void StraightSelectSort<T>(T[] array) where T : IComparable<T>
{for (int i = 0; i < array.Length - 1; i++){int minIndex = i;T min = array[i];for (int j = i + 1; j < array.Length; j++){if (array[j].CompareTo(min) < 0){min = array[j];minIndex = j;}}if (minIndex != i){array[minIndex] = array[i];array[i] = min;}}
}

直接选择排序是不稳定的。

3.2 堆选择排序

直接选择排序并没有把每一趟的比较结果保存下来，在后一趟的比较中，许多比较在前一趟已经做过了，但由于前一趟排序时未保存这些比较结果，所以后一趟排序时又重复执行了这些比较操作，因而执行的比较次数较多。

如果可以做到每次在选择到最小记录的同时，并根据比较结果对其他记录做出相应的调整，那样排序的总体效率就会非常高了。而堆选择排序是一种树形选择排序，是对直接选择排序的有效改进。堆选择排序算法是Floyd和Williams在1964年共同发明的，同时，他们也发明了“堆”这样的数据结构。

堆的概念：具有$n$个元素的序列$K=\{k_1,k_2,\cdots ,k_n\}$当且仅当满足

$$\{\begin{array}{l}{k}_i\le k_{2i}\\ k_i\le k_{2i+1}\end{array},\{\begin{array}{l}{k}_i\ge k_{2i}\\ k_i\ge k_{2i+1}\end{array},i=1,2,\cdots ,\left[\frac{n}{2}\right]$$

时称之为堆。

若关键码的集合$K=\{k_1,k_2,\cdots ,k_n\}$，把它们按照完全二叉树的顺序存放在一维数组中。

• 若满足$k_i\le k_{2i}$且$k_i\le k_{2i+1}$则称作小根堆。
• 若满足$k_i\ge k_{2i}$且$k_i\ge k_{2i+1}$则称作大根堆。

小根堆：int[] Key = new int[]{9,17,65,23,45,78,87,53,31,58,64};

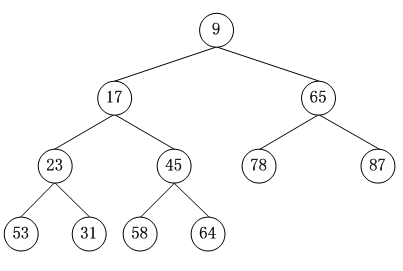
大根堆：int[] Key = new int[]{94,93,75,91,85,44,51,18,48,58,10,34};

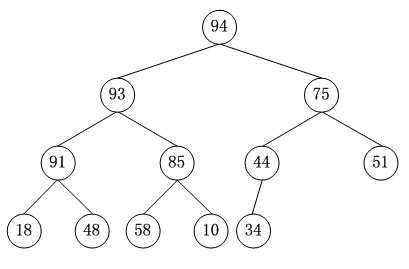
思想（以大根堆为例）：
构建大根堆之后，输出堆顶记录，对剩余的$n-1$个记录接着构建大根堆，便可得到$n$个记录的次大值，如此反复执行，就能得到一个有序序列，这个过程称为堆选择排序。

堆选择排序需解决的两个问题：

问题1：如何建堆，对初始序列建堆的过程，就是一个反复进行筛选的过程。

• （1）对一棵具有$n$个结点的完全二叉树来说最后一个结点是第$[\frac{n}{2}]$个结点的子树。
• （2）筛选从第$[\frac{n}{2}]$个结点为根的子树开始，该子树成为堆。
• （3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。

即把序号为$[\frac{n}{2}],[\frac{n}{2}]-1,\cdots ,1$，的记录作为根的子树都调整为堆。

问题2：输出堆顶元素后，如何调整新堆。

• （1）设有$n$个元素的堆，输出堆顶元素后，剩下$n-1$个元素。将堆底元素送入堆顶（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。
• （2）将根结点与左，右子树中较大元素进行交换。
• （3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复第二步。
• （4）若与右子树交换：如果右子树堆被破坏，即右子树的根结点不满足堆的性质，则重复第二步。
• （5）继续对不满足堆性质的子树进行上述操作，直到叶子结点，堆被重建成。

即：输出堆顶元素，将最后一个叶子结点放在堆顶，重新构建大根堆。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

排序过程：

初始时：$Key1\to -1,45,\overline{34},78,12,34,32,29,64$

建堆后：$Key1\to -1,78,64,45,\overline{34},34,32,29,12$

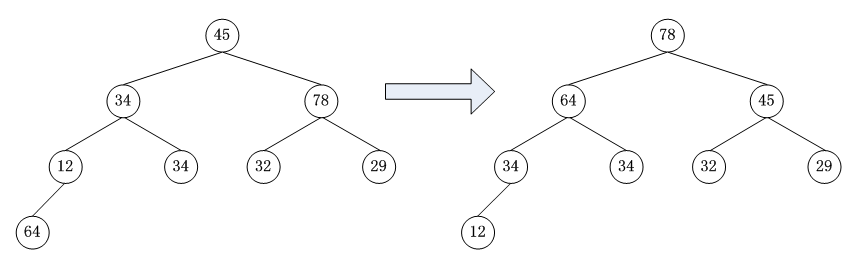
堆重建后：

$Key1\to -1,64,\overline{34},45,12,34,32,29,[78]$

$Key1\to -1,45,\overline{34},32,12,34,29,[64,78]$

$Key1\to -1,\overline{34},34,32,12,29,[45,64,78]$

$Key1\to -1,34,29,32,12,[\overline{34},45,64,78]$

$Key1\to -1,32,29,12,[34,\overline{34},45,64,78]$

$Key1\to -1,29,12,[32,34,\overline{34},45,64,78]$

$Key1\to -1,12,[29,32,34,\overline{34},45,64,78]$

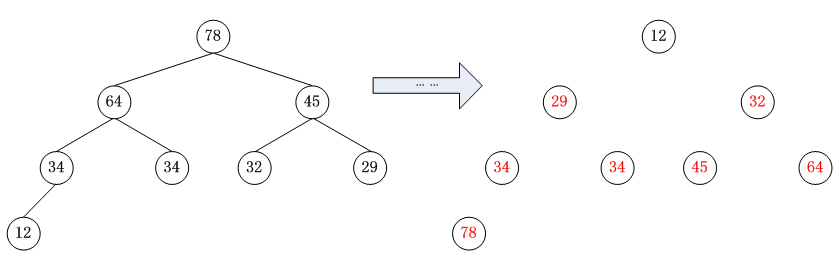
程序代码：

private static void Restore<T>(T[] array, int j, int vCount) where T : IComparable<T>
{//构建以结点j为根,一共有vCount个结点的大根堆while (j <= vCount / 2){int m = (2 * j + 1 <= vCount && array[2 * j + 1].CompareTo(array[2 * j]) > 0)? 2 * j + 1: 2 * j;if (array[m].CompareTo(array[j]) > 0){T temp = array[m];array[m] = array[j];array[j] = temp;j = m;}else{break;}}
}/// <summary>
/// 堆选择排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void HeapSelectSort<T>(T[] array) where T : IComparable<T>
{int vCount = array.Length;T[] tempArray = new T[vCount + 1];for (int i = 0; i < vCount; i++)tempArray[i + 1] = array[i];//初建大根堆for (int i = vCount / 2; i >= 1; i--)Restore(tempArray, i, vCount);//大根堆的重构与排序for (int i = vCount; i > 1; i--){T temp = tempArray[i];tempArray[i] = tempArray[1];tempArray[1] = temp;Restore(tempArray, 1, i - 1);}for (int i = 0; i < vCount; i++)array[i] = tempArray[i + 1];
}

4. 交换排序

4.1 冒泡交换排序

思想：通过相邻记录之间的比较和交换，使关键字较小的记录如气泡一般逐渐向上漂移直至水面。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

$i=0\to [12],45,\overline{34},78,29,34,32,64$

$i=1\to [12,29],45,\overline{34},78,32,34,64$

$i=2\to [12,29,32],45,\overline{34},78,34,64$

$i=3\to [12,29,32,\overline{34}],45,34,78,64$

$i=4\to [12,29,32,\overline{34},34],45,64,78$

$i=5\to [12,29,32,\overline{34},34,45],64,78$

$i=6\to [12,29,32,\overline{34},34,45,64],78$

程序代码：

/// <summary>
/// 冒泡交换排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void BubbleExchangeSort<T>(T[] array) where T : IComparable<T>
{for (int i = 0; i < array.Length - 1; i++){for (int j = array.Length - 1; j > i; j--){if (array[j].CompareTo(array[j - 1]) < 0){T temp = array[j - 1];array[j - 1] = array[j];array[j] = temp;}}}
}

对冒泡排序常见的改进方法是加入一个标志性变量flag，用于标志某一趟排序过程是否有数据交换，如果进行某一趟排序时并没有进行数据交换，则说明数据已经按要求排列好，可立即结束排序，避免不必要的比较过程。

程序代码：

/// <summary>
/// 改进的冒泡交换排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void BubbleExchangeSortImproved<T>(T[] array) where T : IComparable<T>
{for (int i = 0; i < array.Length - 1; i++){bool flag = false;for (int j = array.Length - 1; j > i; j--){if (array[j].CompareTo(array[j - 1]) < 0){T temp = array[j - 1];array[j - 1] = array[j];array[j] = temp;flag = true;}}if (flag == false)break;}
}

4.2 快速交换排序

快速交换排序是由图灵奖获得者Tony Hoare（东尼.霍尔）所发展的一种排序算法，是采用分治策略的一个非常典型的应用。快速交换排序虽然高端，但其思想是来自冒泡交换排序的，冒泡交换排序是通过相邻元素的比较和交换把最小的冒泡到最顶端，而快速交换排序是比较和交换小数和大数，这样一来不仅小数冒泡到上面的同时也把大数沉到下面。

其基本思想如下：

• （1）选择一个基准元素，通常选择第一个元素或者最后一个元素。
• （2）通过一趟排序将待排序的记录分割成独立的两部分，其中一部分记录的元素值均比基准元素值小，另一部分记录的元素值比基准值大。
• （3）此时基准元素在其排好序的正确位置。
• （4）然后分别对这两部分记录用同样的方法继续进行排序，直到整个序列有序。

即：从待排记录中选一记录，将其放入正确的位置，然后以该位置为界，对左右两部分再做快速排序，直到划分的长度为1。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

$init\to 45,\overline{34},78,12,34,32,29,64$

$step1\to [32,\overline{34},29,12,34],45,[78,64]$

$step2\to [[29,12],32,[\overline{34},34]],45,[78,64]$

$step3\to [[[12],29],32,[\overline{34},34]],45,[78,64]$

$step4\to [[[12],29],32,[[34],\overline{34}]],45,[78,64]$

$step5\to [[[12],29],32,[[34],\overline{34}]],45,[[64],78]$

程序代码：

private static void QuickSort<T>(T[] array, int left, int right) where T : IComparable<T>
{//快速排序递归函数if (left < right){T current = array[left];int i = left;int j = right;while (i < j){while (array[j].CompareTo(current) > 0 && i < j)j--;while (array[i].CompareTo(current) <= 0 && i < j)i++;if (i < j){T temp = array[i];array[i] = array[j];array[j] = temp;j--;i++;}}array[left] = array[j];array[j] = current;if (left < j - 1) QuickSort(array, left, j - 1);if (right > j + 1) QuickSort(array, j + 1, right);}
}/// <summary>
/// 快速交换排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void QuickExchangeSort<T>(T[] array) where T : IComparable<T>
{QuickSort(array, 0, array.Length - 1);
}

其实上面的代码还可以再优化，上面代码中基准元素已经在current中保存了，所以不需要每次交换都设置一个temp变量，在交换的时候只需要先后覆盖就可以了。这样既能较少空间的使用还能降低赋值运算的次数。

优化代码如下：

private static void QuickSortImproved<T>(T[] array, int left, int right) where T : IComparable<T>
{//快速排序递归函数if (left < right){T current = array[left];int i = left;int j = right;while (i < j){while (array[j].CompareTo(current) > 0 && i < j)j--;array[i] = array[j];while (array[i].CompareTo(current) <= 0 && i < j)i++;array[j] = array[i];}array[j] = current;if (left < j - 1) QuickSortImproved(array, left, j - 1);if (right > j + 1) QuickSortImproved(array, j + 1, right);}
}/// <summary>
/// 快速交换排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void QuickExchangeSortImproved<T>(T[] array) where T : IComparable<T>
{QuickSortImproved(array, 0, array.Length - 1);
}

5. 并归排序

我们首先先看两个有序序列合并的例子，如：

int[] Key1 = new int[]{1,3,5,7,9};
int[] Key2 = new int[]{2,4,6,8,10,12,14}int[] temp = new int[Key1.Length + Key2.Length];

$temp\to 0,0,0,0,0,0,0,0,0,0,0,0$

$temp\to 1,2,3,4,5,6,7,8,9,0,0,0$

$temp\to 1,2,3,4,5,6,7,8,9,10,12,14$

程序代码：

/// <summary>
/// 合并排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam>
/// <param name="array1">有序记录集合1</param>
/// <param name="array2">有序记录集合2</param>
/// <returns>合并后的有序记录集合</returns>
public static T[] MergeSort<T>(T[] array1,T[] array2) where T : IComparable<T>
{T[] temp = new T[array1.Length + array2.Length];int i = 0, j = 0, k = 0;while (i < array1.Length && j < array2.Length){if (array1[i].CompareTo(array2[i]) < 0){temp[k++] = array1[i++];}else{temp[k++] = array2[j++];}}while (i < array1.Length){temp[k++] = array1[i++];}while (j < array2.Length){temp[k++] = array2[j++];}return temp;
}

我们接着看一个序列的并归排序。

首先递归划分子问题，然后合并结果。把待排序列看成由两个有序的子序列构成，然后合并两个子序列，接着把子序列看成由两个有序序列组成……。倒过来看，其实就是先两两合并，然后四四合并……最终形成有序序列。该算法是采用分治策略的一个非常典型的应用，俗称 2-路并归。

如：int[] Key = new int[]{45,34,78,12,34,32,29,64};

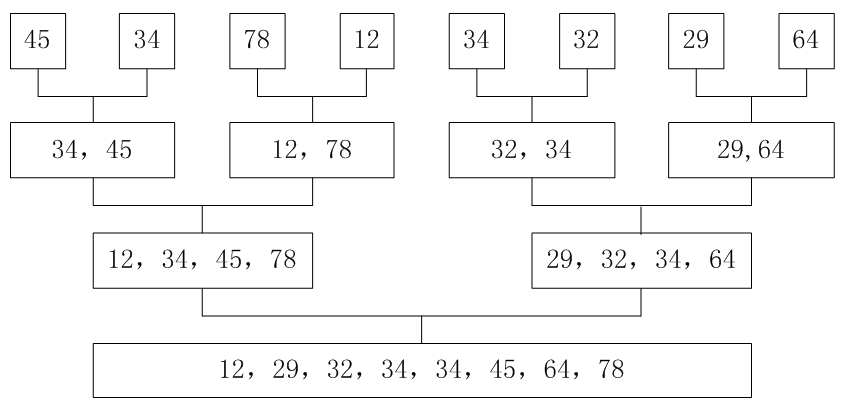
程序代码：

/// <summary>
/// 合并排序的递归合并函数
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam>
/// <param name="array">需要排序的记录集合</param>
/// <param name="left">起点位置</param>
/// <param name="mid">中间位置</param>
/// <param name="right">终点位置</param>
private static void Merge<T>(T[] array, int left, int mid, int right) where T : IComparable<T>
{T[] temp = new T[right - left + 1];int i = left;int j = mid + 1;int k = 0;while (i <= mid && j <= right){if (array[i].CompareTo(array[j]) < 0){temp[k++] = array[i++];}else{temp[k++] = array[j++];}}while (i <= mid){temp[k++] = array[i++];}while (j <= right){temp[k++] = array[j++];}for (int n = 0; n < temp.Length; n++){array[left + n] = temp[n];}
}/// <summary>
/// 合并排序的递归分治函数
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
/// <param name="left">起点位置</param>
/// <param name="right">终点位置</param>
private static void MergeSort<T>(T[] array, int left, int right) where T : IComparable<T>
{if (left >= right)return;int mid = (left + right) / 2;MergeSort(array, left, mid); //递归排序左边MergeSort(array, mid + 1, right); //递归排序右边Merge(array, left, mid, right); //合并
}/// <summary>
/// 合并排序
/// </summary>
/// <typeparam name="T">需要排序记录的类型</typeparam> 
/// <param name="array">需要排序的记录集合</param>
public static void MergeSort<T>(T[] array) where T : IComparable<T>
{MergeSort(array, 0, array.Length - 1);
}