线性代数:第二章 矩阵及其运算
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。
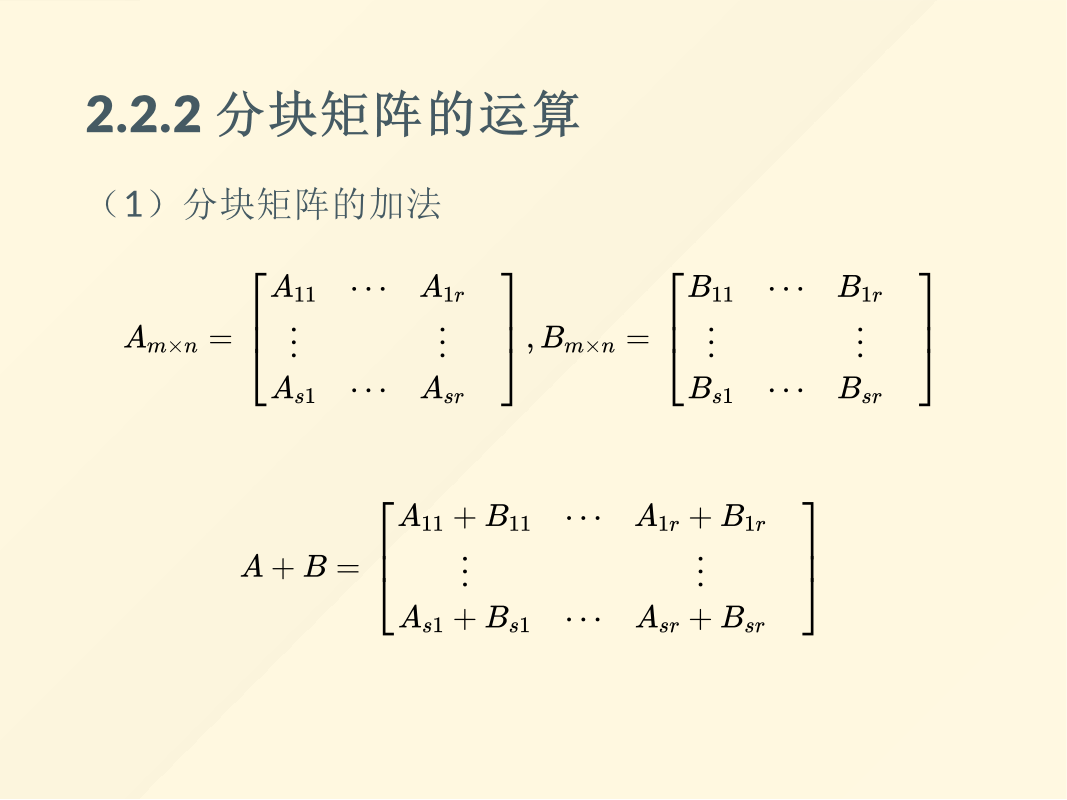
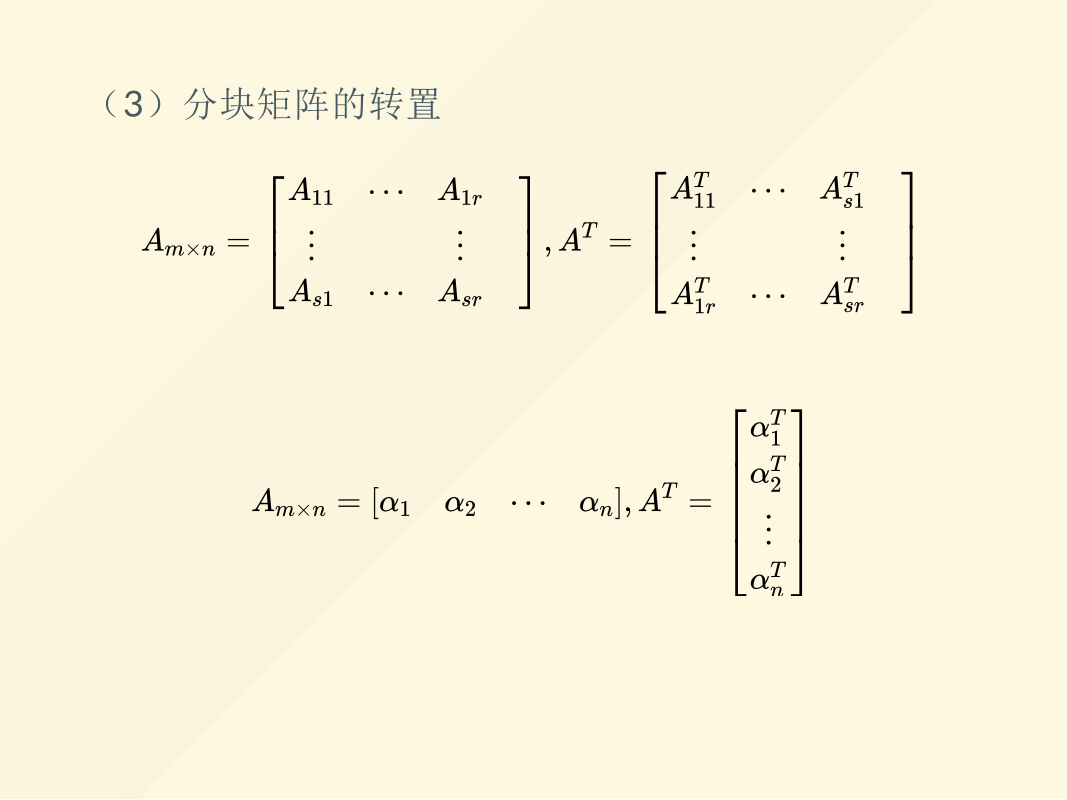
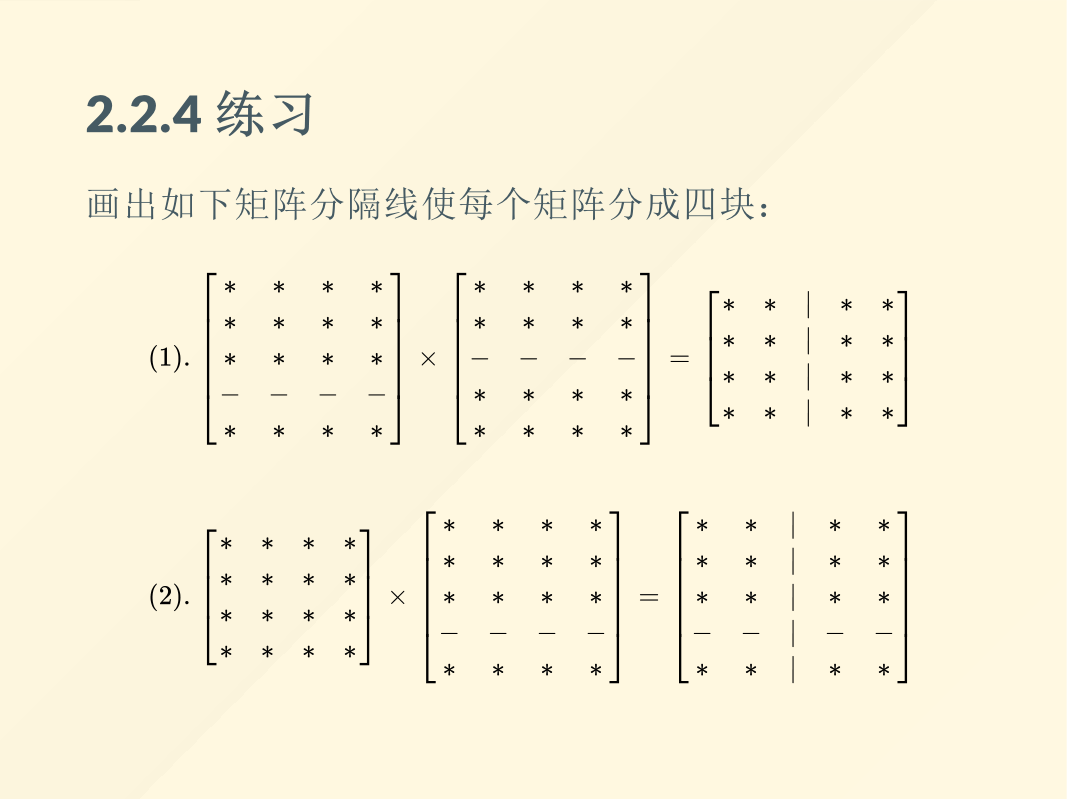
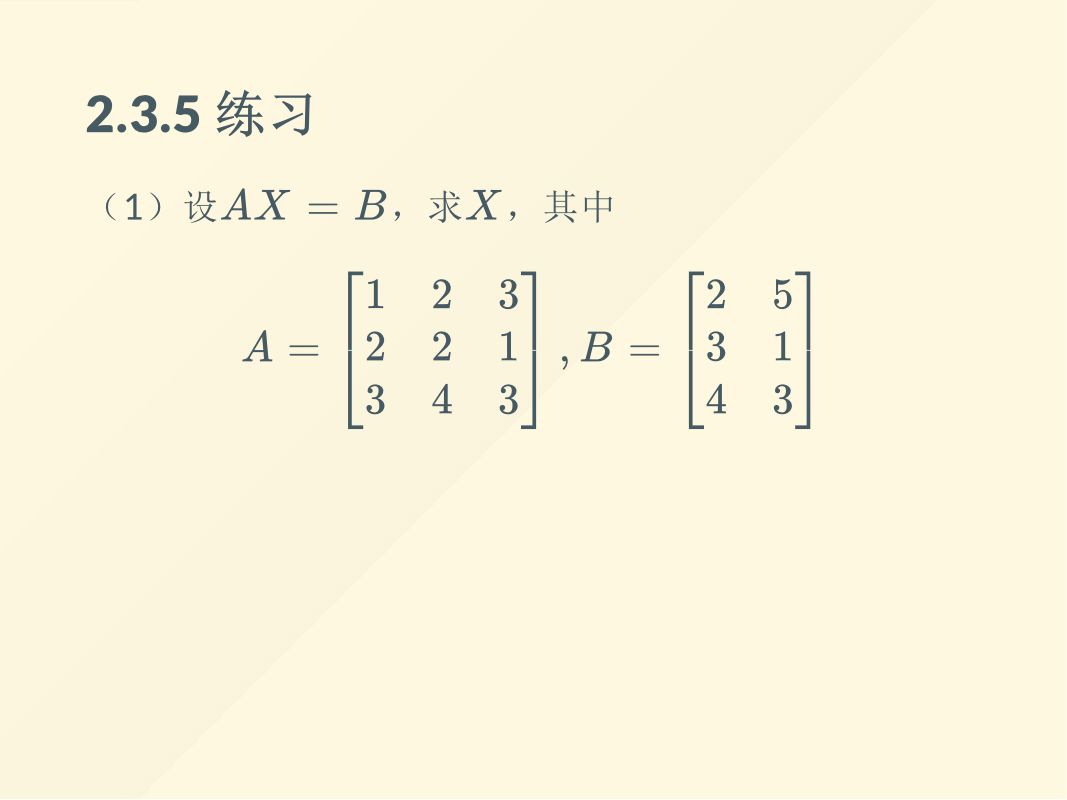
本章主要介绍有关矩阵的知识,主要包括矩阵的基本运算(加法、数乘、乘法、乘幂、迹、转置),其中乘法最为重要,在计算机图形学中具有大量的应用。如果矩阵的行数和列数很大,计算起来不方便,我们就可以对该矩阵进行分块,把对大矩阵的运算转换为对子块的运算。在高中阶段,我们所说的四则运算包括加法、减法、乘法、除法。而矩阵是没有除法运算的,对应于数的除法,矩阵有求逆的运算。在求矩阵的逆矩阵的过程中,我们引入了初等方阵的概念,可利用初等方阵来求矩阵的逆矩阵以及求解矩阵方程。最后我们又讨论了方阵的行列式以及矩阵的LU分解。本章相对于第一章线性方程组就有一些难度了,希望大家好好复习,把基本概念和方法搞明白。
推荐两个学习线性代数的资源:
1. 麻省理工公开课 Linear Algebra
- https://www.bilibili.com/video/av15463995/
- 相较于国内老师从行列式入手,MIT老师从几何空间的角度,更加直观揭示线代的内核。
2. 线性代数的本质
- https://www.bilibili.com/video/BV1ys411472E
- 通过直观的动画演示来理解线性代数的大部分核心概念。
关注本公众号并回复“资料下载”可以获取MIT线性代数公开课英文教材和中文笔记一份,以方便大家学习。








































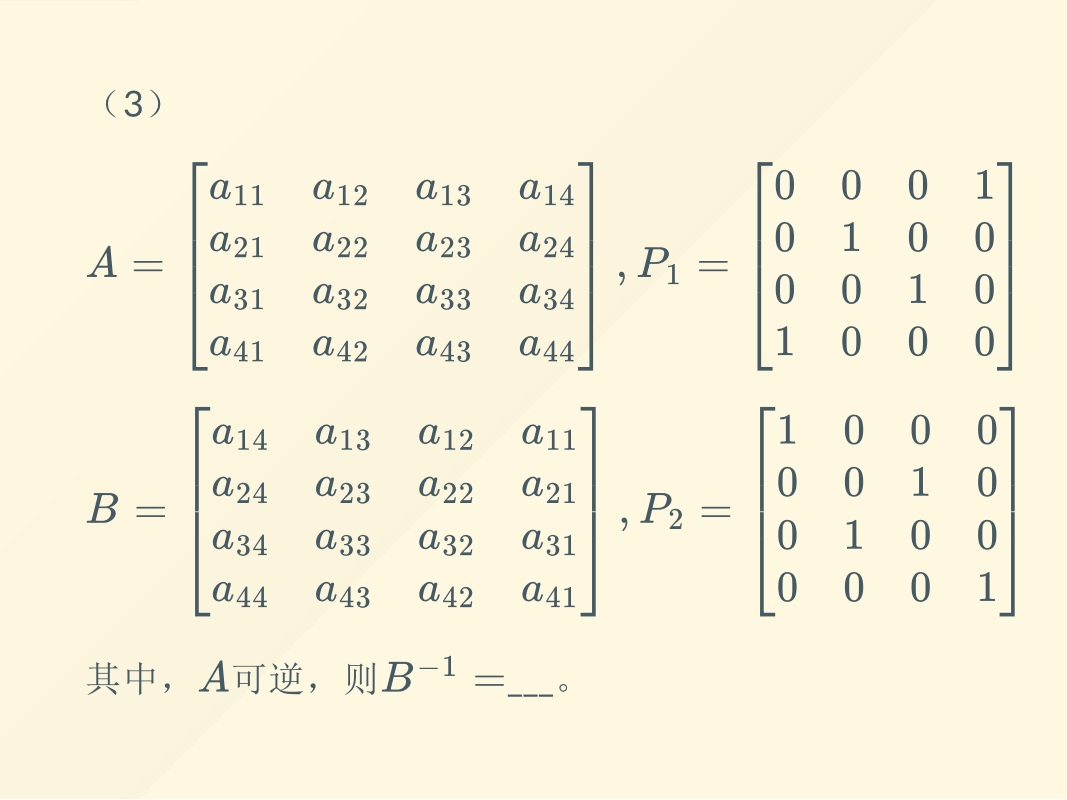




















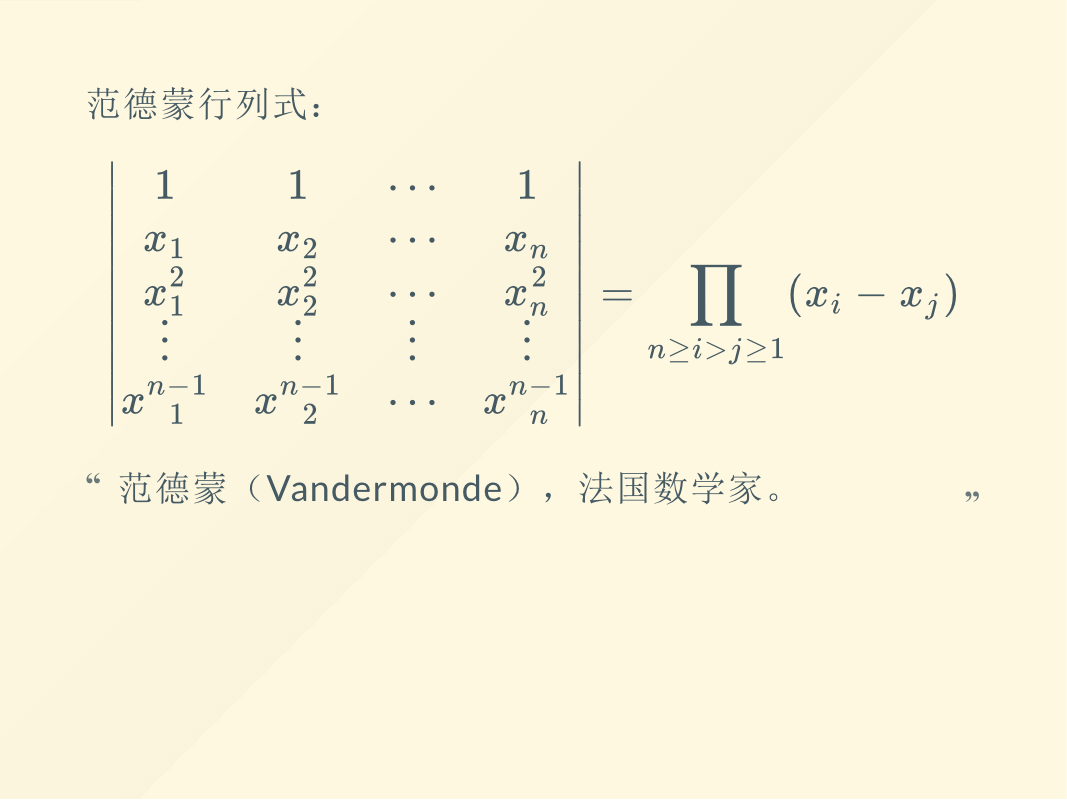
















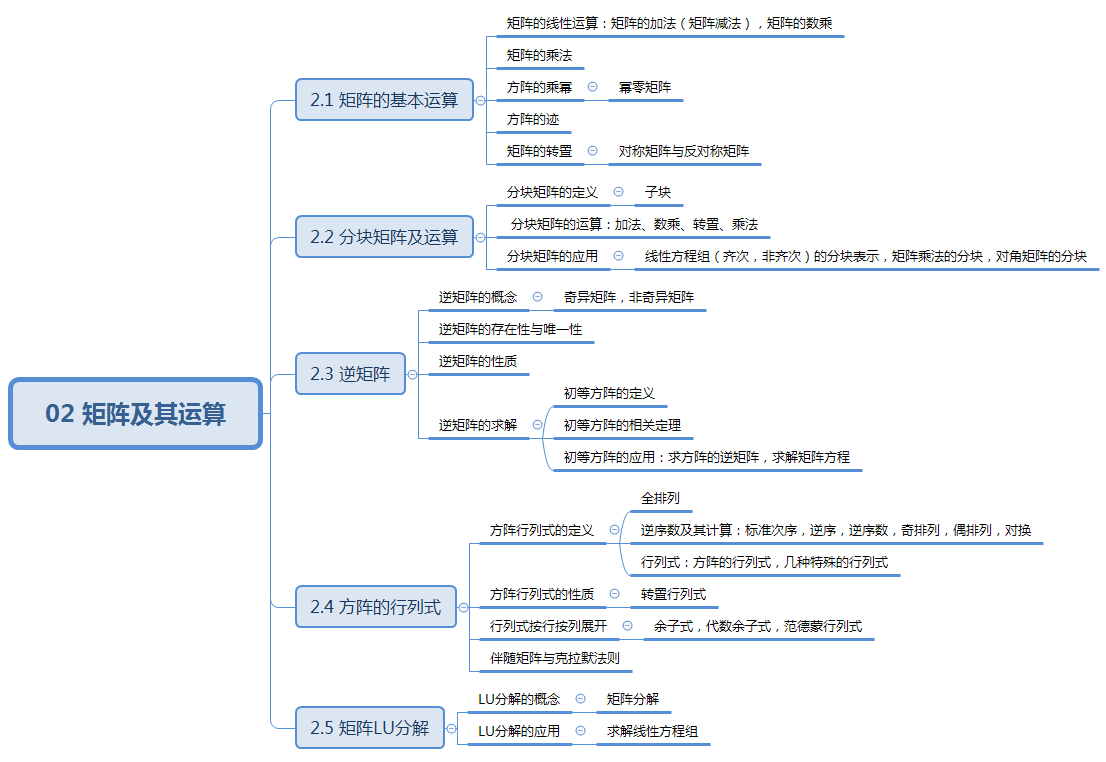

相关文章:

sdut 2401 最大矩形面积
1http://acm.sdut.edu.cn/sdutoj/problem.php?actionshowproblem&problemid2401 /*2 最大矩形面积,把边界点加上3 从左往右 处理一遍;4 再从上往下处理一遍;5 */6 7 #include<stdio.h>8 #define maxn 200009 #include<cmath>…
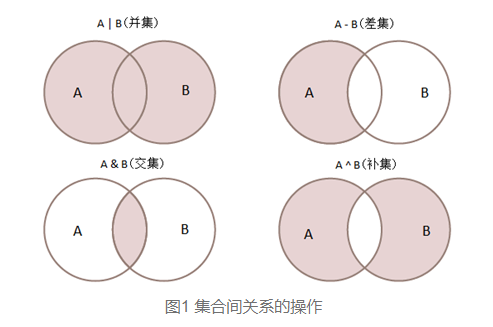
Python中怎样改变集合之间的关系?
Python中怎样改变集合之间的关系?数学中,两个集合关系的常见操作包括:交集、并集、差集、补集。设A,B是两个集合,集合关系的操作介绍如下: 交集是指属于集合A且属于集合B的元素所组成的集合, 并集是指集合…
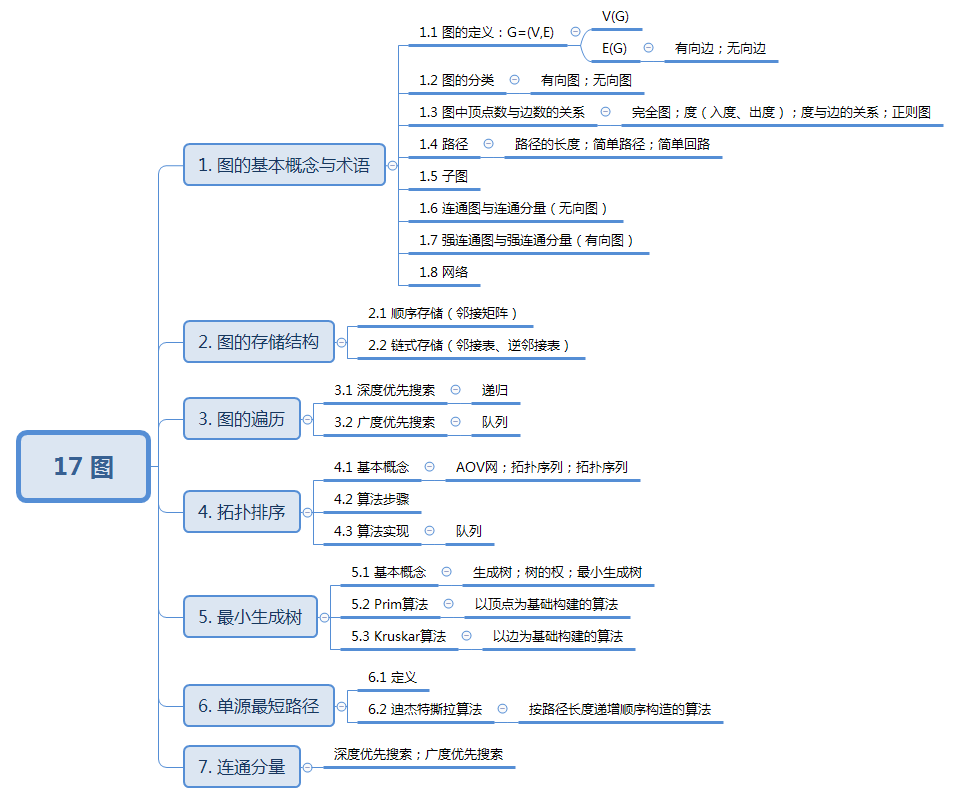
数据结构与算法:17 图
17 图 知识结构: 1. 图的基本概念与术语 1.1 图的定义 图由顶点集和边集组成,记为G(V,E)G(V,E)G(V,E)。 顶点集:顶点的有穷非空集合,记为V(G)V(G)V(G)。边集:顶点偶对的有穷集合,记为E(G)E(G)E(G) 。 …

云计算安全:技术与应用
云计算安全:技术与应用中国电信网络安全实验室 编著ISBN 978-7-121-14409-72012年1月出版定价:59.00元16开236页宣传语:全面了解云计算安全风险、安全防护手段的佳作!内 容 简 介随着云计算的兴起,安全成为云计算能否顺…

再谈HOST文件
前几天弄了一个关于禁止打开某个网站的文章后,觉得这个HOST文件真的挺有意思的。并且也总是想把自己对它新的理解写下来(也许大家都明白了)以下是HOST文件的内容:# Copyright (c) 1993-1999 Microsoft Corp.## This is a sample H…

PMP®考试是什么机构
项目管理对于很多职场中的人来说是以后要发展的一个方向,随着各职业内卷也越来越严重,pmp认证引起了大家的关注,有朋友问:PMP考试是什么机构?下面我们给大家介绍一下。 PMP考试是什么机构?PMP考试认证在我国大陆地区需要三方机构…
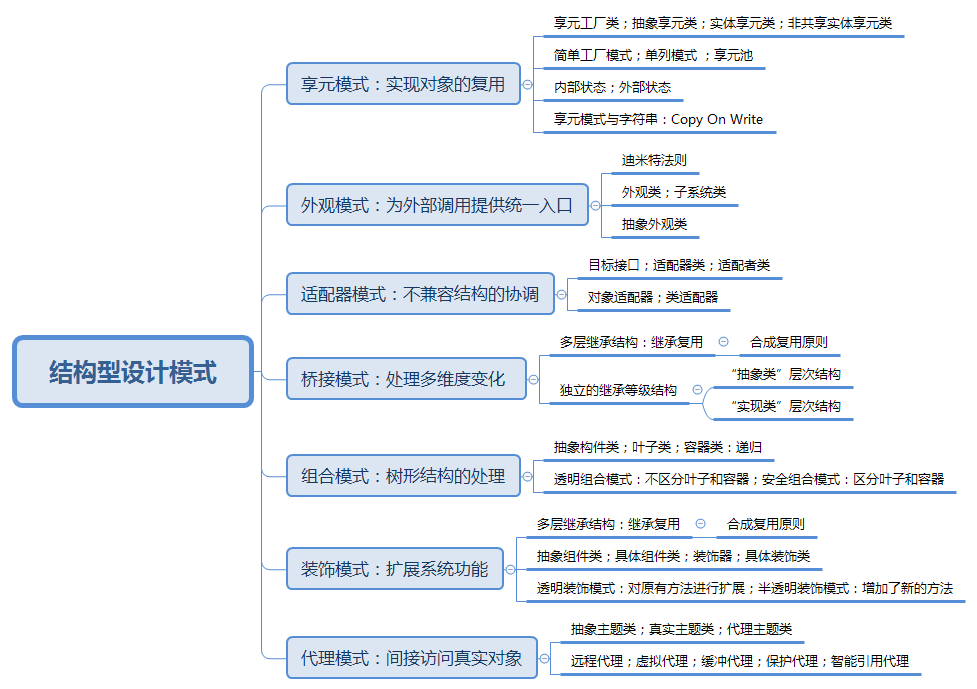
技术图文:03 结构型设计模式(上)
结构型设计模式(上) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 享元模式 – 实现对象的复用 Sunny 软件公司欲开发一个围棋软件,其界面效果如下图所示: 图2 围…

Linux抓包工具tcpdump详解
原文链接 tcpdump是一个用于截取网络分组,并输出分组内容的工具,简单说就是数据包抓包工具。tcpdump凭借强大的功能和灵活的截取策略,使其成为Linux系统下用于网络分析和问题排查的首选工具。 tcpdump提供了源代码,公开了接口&…

学习笔记TF065:TensorFlowOnSpark
2019独角兽企业重金招聘Python工程师标准>>> Hadoop生态大数据系统分为Yam、 HDFS、MapReduce计算框架。TensorFlow分布式相当于MapReduce计算框架,Kubernetes相当于Yam调度系统。TensorFlowOnSpark,利用远程直接内存访问(Remote Direct Memo…

HTML5培训好不好
HTML5培训好不好?这个问题,要看你选择的培训机构,想要学习HTML5技术,靠谱的培训机构非常重要,下面我们就来看看详细的介绍吧。 HTML5培训好不好?从前端开发的基础出发,学习使用HTML,CSS,JavaS…

技术图文:03 结构型设计模式(下)
结构型设计模式(下) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 组合模式 – 树形结构的处理 Sunny 软件公司欲开发一个杀毒(AntiVirus)软件,该软件…

程序员必知8大排序3大查找(三)
前两篇 《程序员必知8大排序3大查找(一)》 《程序员必知8大排序3大查找(二)》 三种查找算法:顺序查找,二分法查找(折半查找),分块查找,散列表(以后谈…
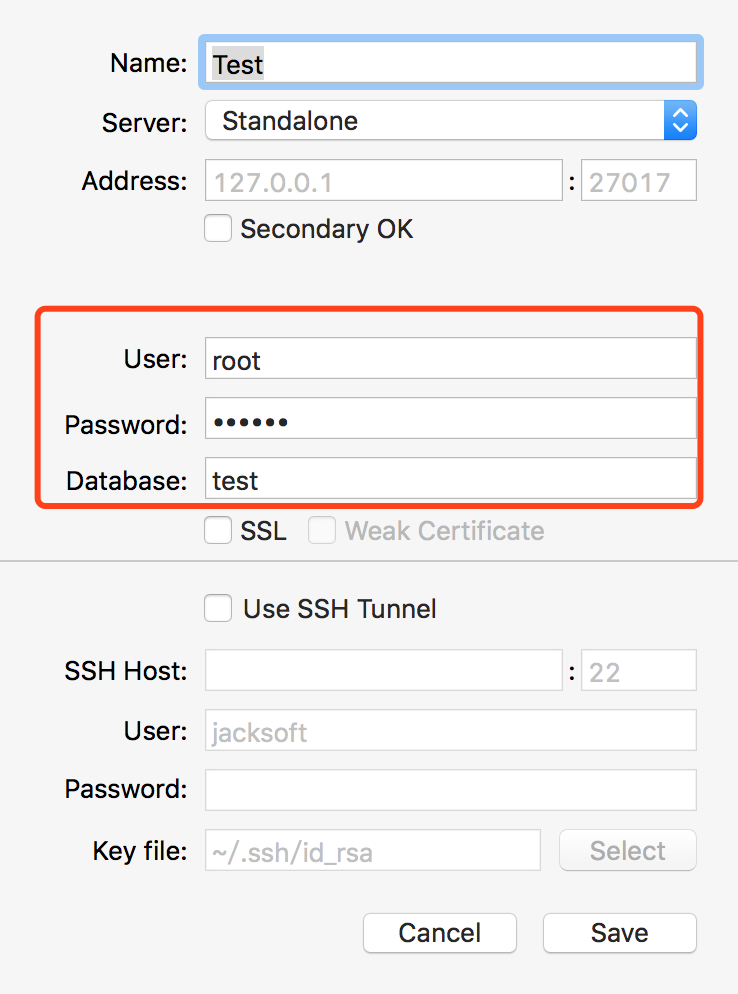
MongoDB给数据库创建用户
转自http://www.imooc.com/article/18439 一.先以非授权的模式启动MongoDB非授权: linux/Mac : mongod -f /mongodb/etc/mongo.confwindows : mongod --config c:\mongodb\etc\mongo.conf 或者 net start mongodb (前提是mongo安装到了服务里面ÿ…

如何挑选一家好的软件测试培训机构
随着智能时代的发展,我们的手机APP等各种软件都变得越来越复杂化、规模化,软件测试这一步骤是必不可少的,这也造就了这个行业的兴起,越来越多的人想要学习软件测试技术,想要知道如何挑选一家好的软件测试培训机构?来看…

POJ 3177 判决素数个数
时间限制: 1000ms内存限制:65536kB描述输入两个整数X和Y,输出两者之间的素数个数(包括X和Y)。输入两个整数X和Y,X和Y的大小任意。输出输出一个整数,结果可以是0,或大于0的整数。样例输入1 100样例输出25&am…

数据结构与算法:22 精选练习50
精选练习50 马上就要期末考试或者考研了。为了大家复习的方便,我精选了有关数据结构与算法的50道选择题,大家可以抽空练习一下。公众号后台回复“答案”可以获取该50道题目的答案。 01、数据在计算机中的表示称为数据的______。 (A&#x…

极速理解设计模式系列:11.单例模式(Singleton Pattern)
单例模式:确保某一个类只有一个实例,而且自行实例化并向整个系统提供这个实例。这个类称为单例类。 三要点: 一、单例类只能有一个实例 二、单例类必须自行创建自身实例 三、单例类自行向整个系统提供实例 类图: 应用场景…

参加web前端培训要学哪些知识
IT行业,web前端技术是比较吃香的,也是工资待遇非常高的行业之一,如果想要做一名合格的web前端工程师,系统学习是非常重要的,那么参加web前端培训要学哪些知识呢?来看看下面的详细介绍。 参加web前端培训要学哪些知识?…
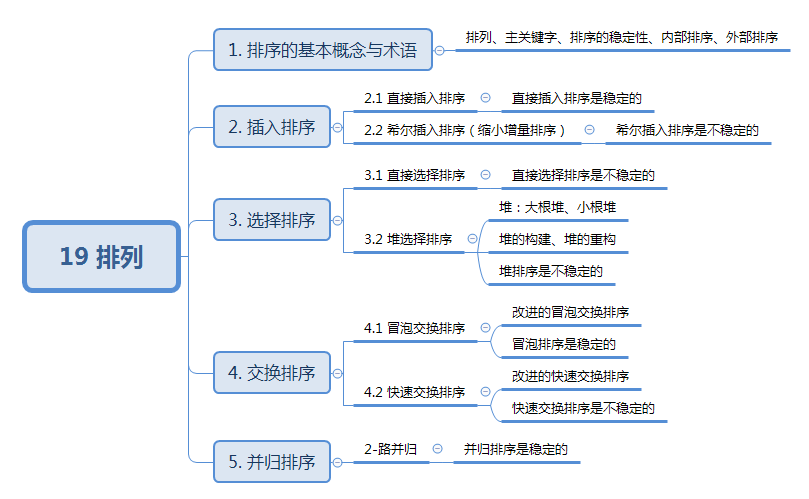
数据结构与算法:19 排序
19 排序 知识结构: 1. 排序的基本概念与术语 假设含有nnn个记录的序列为{r1,r2,⋯,rn}\lbrace r_1,r_2,\cdots,r_n \rbrace{r1,r2,⋯,rn},其相应的关键字分别为{k1,k2,⋯,kn}\lbrace k_1,k_2,\cdots,k_n \rbrace{k1,k2,⋯,kn},…

Objective-C 什么是类
Objective-C 什么是类 转自http://www.189works.com/article-31219-1.html 之前一直做C开发,最近2个多月转 Objective-C, 入门的时候,遇到了很多的困惑。现在过节,正是解决他们的好时机。 主要参考来自http://www.sealiesoftware.…

APP之红点提醒三个阶段
下面这个页面就是我们进入APP后的主界面。客户选项的红点上数字就是显示我们没有查看的客户总数量。 当我们切换到客户这个fragment时,会显示贷款客户数量与保险客户数量。 当我们随便点击入一个选项,假如进入到保险客户的这个activity里面,L…

零基础参加java培训的系统学习路线
零基础想要学习java技术,那么最好的选择就是参加java培训,进行系统的学习,以下就是小编为大家整理的零基础参加java培训的系统学习路线,希望能够帮助到正在学习java技术的零基础同学。 零基础参加java培训的系统学习路线&#…

在ASP.NET中跟踪和恢复大文件下载
在Web应用程序中处理大文件下载的问题一直出了名的困难,因此对于大多数站点来说,如果用户的下载被中断了,它们只能说悲哀降临到用户的身上了。但是我们现在不必这样了,因为你可以使自己的ASP.NET应用程序有能力支持可恢复…

ZeroMQ实例-使用ZeroMQ进行windows与linux之间的通信
1、本文包括 1)在windows下使用ZMQ 2)在windows环境下与Linux环境下进行网络通信 2、在Linux下使用ZMQ 之前写过一篇如何在Linux环境下使用ZMQ的文章 《ZeroMQ实例-使用ZMQ(ZeroMQ)进行局域网内网络通信》,这里就不再赘述。 3、在Windows环境…

线性代数:03 向量空间 -- 基本概念
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点…

如何获得PMP认证证书
pmp证书是一项由美国项目管理协会发起的项目管理专业人士认证证书,它属于国际认证类证书,含金量是非常高的,那么如何获得PMP认证证书呢?来看看下面的详细介绍。 如何获得PMP证书? PMP证书的获取是需要参加PMP考试的。我国自1999年引进PM…

UITextField的详细使用
UItextField通常用于外部数据输入,以实现人机交互。下面以一个简单的登陆界面来讲解UItextField的详细使用。//用来显示“用户名”的labelUILabel* label1 [[UILabelalloc] initWithFrame:CGRectMake(15, 65, 70, 30)];label1.backgroundCol…

06-hibernate注解-一对多单向外键关联
一对多单向外键 1,一方持有多方的集合,一个班级有多个学生(一对多)。 2,OneToMany(cascade{CascadeType.ALL}, fetchFetchType.LAZY ) //级联关系,抓取策略:懒加载。 JoinColumn(name"c…

线性代数:03 向量空间 -- 矩阵的零空间,列空间,线性方程组解的结构
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍向量空间的知识,与前两章一样本章也可以通过研究解线性方程组的解把所有知识点…

学Python培训有什么用
Python在近几年的发展非常迅速,在互联网行业Python的薪资也越来越高,不少人开始准备学习Python技术,那么到底学Python培训有什么用呢?来看看下面的详细介绍。 学Python培训有什么用? 学习python可以提高工作效率,使用python&…
