数据结构与算法:15 树
15 树
知识结构:
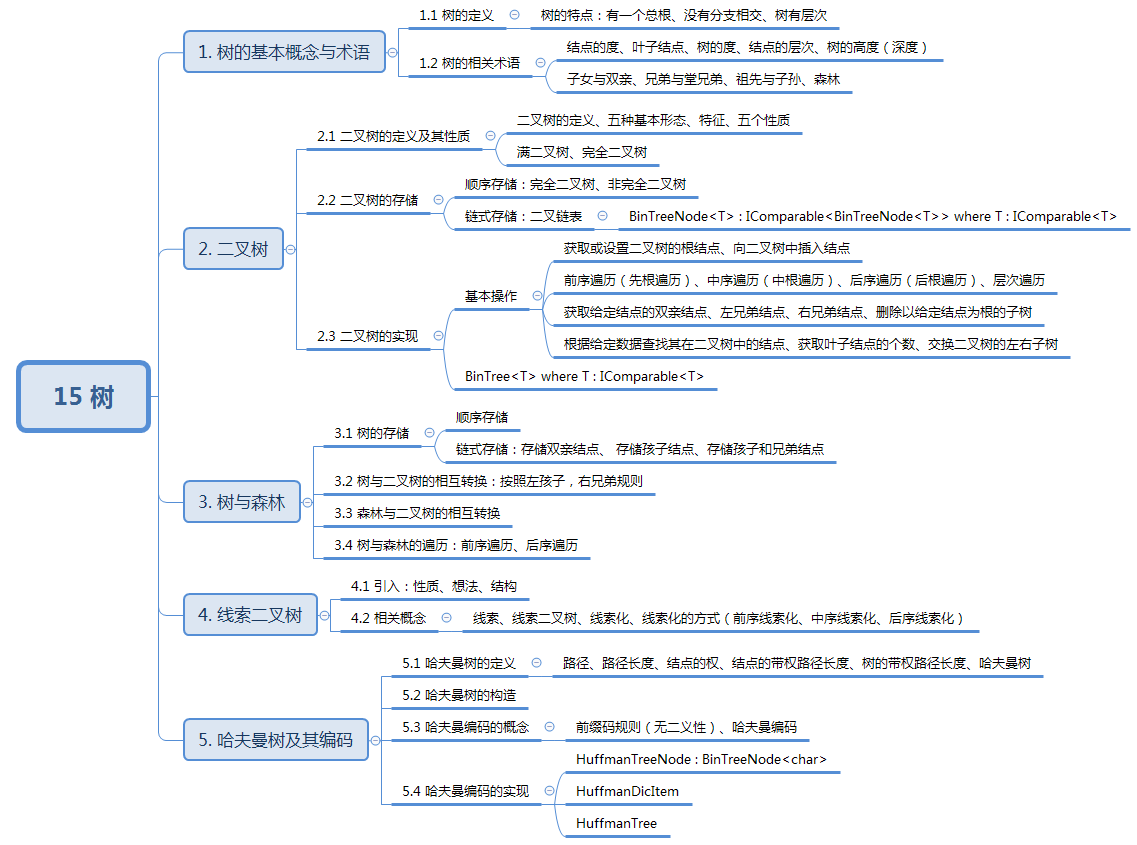
1. 树的基本概念与术语
1.1 树的定义
树是N(N≥0)N(N \geq 0)N(N≥0)个结点组成的有穷集合 ,该集合具有如下特征:
(1)除N=0N=0N=0的树外,有且仅有一个特定的称为根的结点。
(2)其余结点分为m(m≥0)m (m\geq 0)m(m≥0)个互不相交的有穷集合T1,T2,⋯,TmT_1,T_2,\cdots,T_mT1,T2,⋯,Tm,其中每一个集合都是一棵树,称为该根的子树。
例:
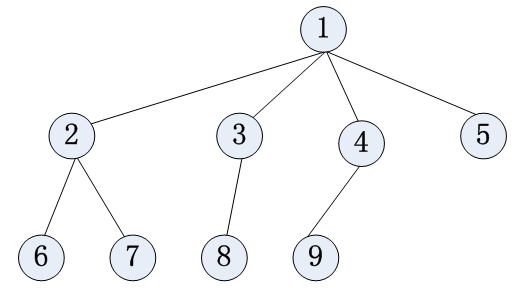
树的特点:
(1)有一个总根。
(2)没有分支相交。
(3)树有层次。
1.2 树的相关术语
结点的度:该结点具有子树的数目。
叶子结点:度为零的结点。(没有子树的结点)
树的度:树中结点度的最大值。
子女与双亲:子女指该结点子树的根结点,双亲即该结点。
结点的层次(Level):根到该结点的路径长度。(根为第零层、若结点XXX在LLL层,则其子女在L+1L+1L+1层)。
树的高度(深度):树中结点层的最大值。
兄弟与堂兄弟:同一双亲孩子之间称为兄弟,其双亲在同一层的结点互为堂兄弟。
祖先与子孙:从根到该结点所经分支上的所有结点称为该结点的祖先,以该结点为根的子树中的所有结点称为该结点的子孙。
森林:m(m≥0)m (m \geq 0)m(m≥0)棵互不相交的树的集合。
2. 二叉树
2.1 二叉树的定义及其性质
(1)二叉树的定义
二叉树是结点的有穷集合,且必须满足下面的条件之一:
- 它是空集。
- 它由一个根结点和其左右子树构成且其左右子树满足二叉树的定义。
(2)二叉树的基本形态
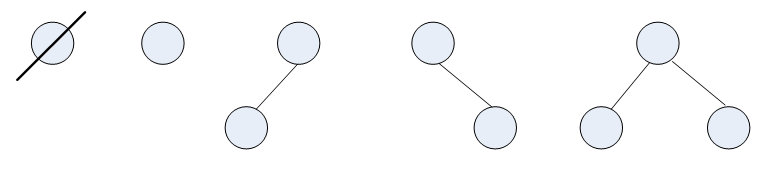
(3)二叉树的特征
- 二叉树的每个结点的度不大于2。
- 二叉树的子树有左右之分。
(4)二叉树的性质
性质1:二叉树中层数为i(i≥0)i(i\geq 0)i(i≥0)的结点至多有2i2^i2i个。
性质2:高度为kkk的二叉树至多有2k+1−1(k≥0)2^{k+1}-1(k\geq 0)2k+1−1(k≥0)个结点。
若一棵高度为kkk的二叉树,具有2k+1−12^{k+1}-12k+1−1个结点,这样的二叉树称为满二叉树。
若一棵具有nnn个结点,高度为kkk的二叉树,其中所有结点与高度为kkk的满二叉树中编号由1至nnn的那些结点对应,这样的二叉树称为完全二叉树。
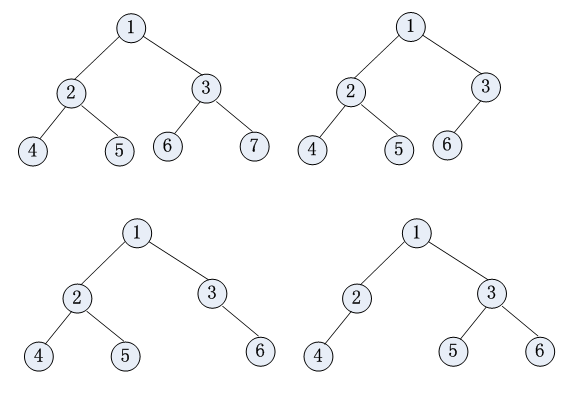
注:满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
性质3:设二叉树中叶子结点的个数为n0n_0n0,度为2结点的个数为n2n_2n2,则n0=n2+1n_0=n_2+1n0=n2+1。
性质4:将一棵具有nnn个结点的完全二叉树按层次顺序(从上到下、从左到右)从1开始编号,则对编号为i(1≤i≤n)i(1\leq i\leq n)i(1≤i≤n)的结点有:
- 若iii不等于1,则编号为iii结点的双亲结点的编号为[i2][\frac{i}{2}][2i];
- 若2i≤n2i\leq n2i≤n,则编号为iii结点的左孩子的编号为2i2i2i,否则iii无左孩子;
- 若2i+1≤n2i+1 \leq n2i+1≤n,则编号为iii结点的右孩子的编号为2i+12i+12i+1,否则iii无右孩子;
性质5:具有nnn个结点的完全二叉树的高度为[log2n][log_2^n][log2n]。
2.2 二叉树的存储
(1)顺序存储
完全二叉树:
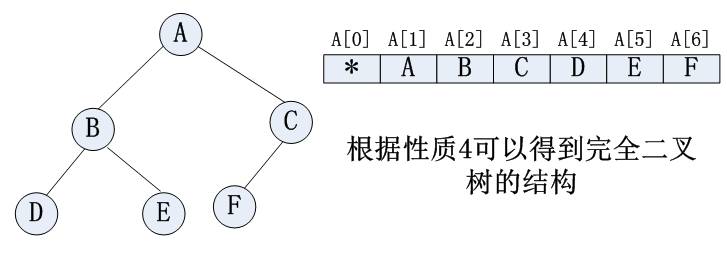
非完全二叉树:
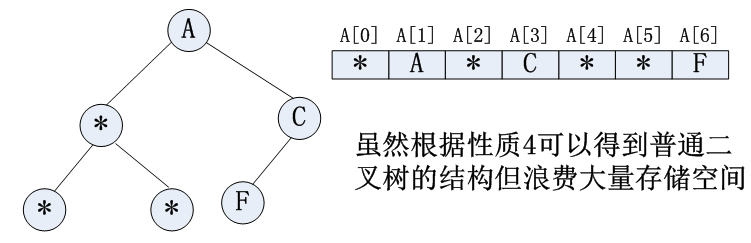
(2)链式存储
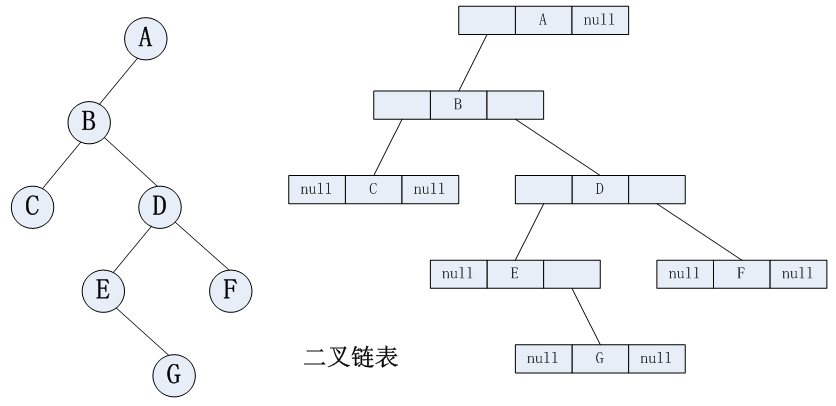
通常:完全二叉树用顺序存储,普通二叉树用链式存储。
二叉树结点的结构:
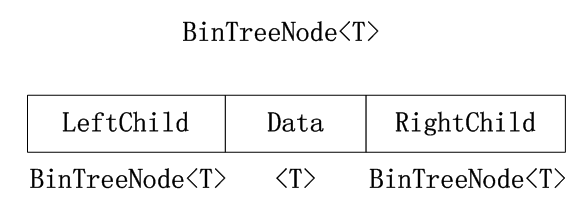
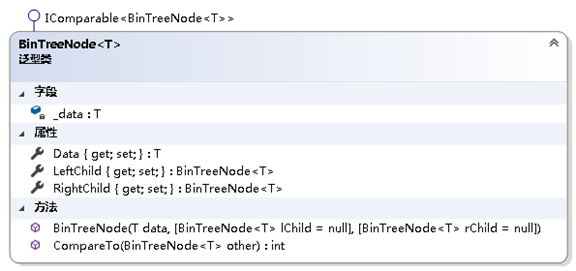
using System;
namespace NonLinearStruct
{/// <summary>/// 二叉树结点/// </summary>/// <typeparam name="T">结点中数据元素的类型</typeparam>public class BinTreeNode<T> : IComparable<BinTreeNode<T>> where T : IComparable<T>{private T _data;/// <summary>/// 获取或设置该结点的左孩子/// </summary>public BinTreeNode<T> LeftChild { get; set; }/// <summary>/// 获取或设置该结点的右孩子/// </summary>public BinTreeNode<T> RightChild { get; set; }/// <summary>/// 获取或设置该结点的数据元素/// </summary>public T Data{get { return _data; }set{if (value == null)throw new ArgumentNullException();_data = value;}}/// <summary>/// 初始化BinTreeNode类的新实例/// </summary>/// <param name="lChild">该结点的左孩子</param>/// <param name="data"> 该结点的数据元素 </param>/// <param name="rChild">该结点的右孩子</param>public BinTreeNode(T data, BinTreeNode<T> lChild = null, BinTreeNode<T> rChild = null){if (data == null)throw new ArgumentNullException();LeftChild = lChild;_data = data;RightChild = rChild;}/// <summary>/// 实现接口IComparable<BinTreeNode<T>>中的方法。/// </summary>/// <param name="other"></param>/// <returns></returns>public int CompareTo(BinTreeNode<T> other){if (other == null)throw new ArgumentNullException();return _data.CompareTo(other.Data);}}
}
2.3 二叉树的遍历
定义:按照一定次序访问树中所有结点,并且每个结点的值仅被访问一次的过程。
遍历的方式:
- 前序遍历(先根遍历):访问根结点,前序遍历左子树,前序遍历右子树;
- 中序遍历(中根遍历):中序遍历左子树,访问根结点,中序遍历右子树;
- 后序遍历(后根遍历):后序遍历左子树,后序遍历右子树,访问根结点
- 层次遍历:遍历第0层,遍历第1层,⋯\cdots⋯,遍历第kkk层(kkk为树的深度);
例子:
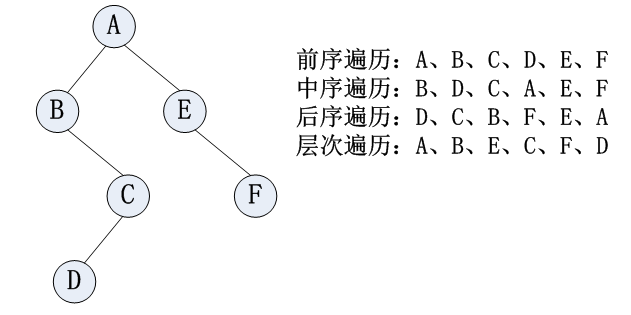
例子:中序遍历与递归

2.4 二叉树的实现
二叉树的操作
- 获取或设置二叉树的根结点
- 向二叉树中插入结点
- 获取前序遍历序列
- 获取中序遍历序列
- 获取后序遍历序列
- 获取层次遍历序列
- 获取给定结点的双亲结点
- 获取给定结点的左兄弟结点
- 获取给定结点的右兄弟结点
- 删除以给定结点为根的子树
- 根据给定数据查找其在二叉树中的结点
- 获取叶子结点的个数
- 交换二叉树的左右子树
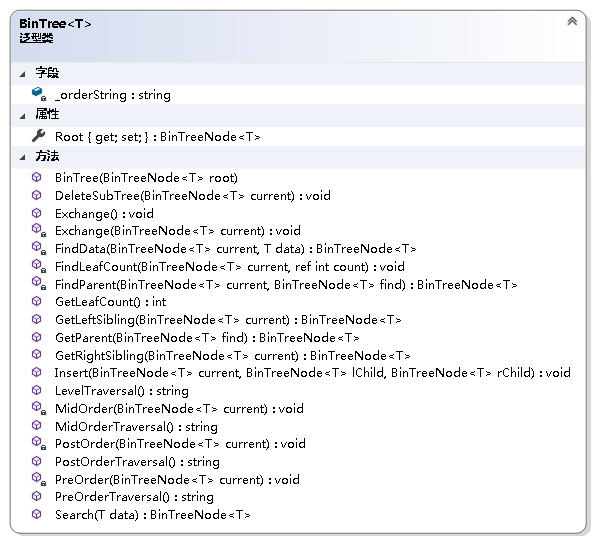
using System;
using LinearStruct;
namespace NonLinearStruct
{/// <summary>/// 二叉树的抽象数据类型实现/// </summary>/// <typeparam name="T">二叉树中结点数据的类型</typeparam>public class BinTree<T> where T : IComparable<T>{private string _orderString = string.Empty;/// <summary>/// 获取或设置二叉树的根结点/// </summary>public BinTreeNode<T> Root { get; set; }/// <summary>/// 初始化BinTree类的新实例/// </summary>/// <param name="root">二叉树的根结点</param>public BinTree(BinTreeNode<T> root){Root = root;}/// <summary>/// 向树中插入结点/// </summary>/// <param name="current">要插入的结点</param>/// <param name="lChild">该结点的左孩子结点</param>/// <param name="rChild">该结点的右孩子结点</param>public void Insert(BinTreeNode<T> current, BinTreeNode<T> lChild, BinTreeNode<T> rChild){if (Root == null)throw new Exception("树为空.");if (current == null)throw new ArgumentNullException();current.LeftChild = lChild;current.RightChild = rChild;}/// <summary>/// 前序遍历的递归函数/// </summary>/// <param name="current">开始递归的根结点</param>private void PreOrder(BinTreeNode<T> current){if (current == null)return;_orderString += current.Data + " ";PreOrder(current.LeftChild);PreOrder(current.RightChild);}/// <summary>/// 得到前序遍历序列/// </summary>/// <returns>前序遍历序列</returns>public string PreOrderTraversal(){_orderString = string.Empty;PreOrder(Root);return _orderString.Trim();}/// <summary>/// 中序遍历的递归函数/// </summary>/// <param name="current">开始递归的根结点</param>private void MidOrder(BinTreeNode<T> current){if (current == null)return;MidOrder(current.LeftChild);_orderString += current.Data + " ";MidOrder(current.RightChild);}/// <summary>/// 得到中序遍历序列/// </summary>/// <returns>中序遍历序列</returns>public string MidOrderTraversal(){_orderString = string.Empty;MidOrder(Root);return _orderString.Trim();}/// <summary>/// 后序遍历的递归函数/// </summary>/// <param name="current">开始递归的根结点</param>private void PostOrder(BinTreeNode<T> current){if (current == null)return;PostOrder(current.LeftChild);PostOrder(current.RightChild);_orderString += current.Data + " ";}/// <summary>/// 得到后序遍历序列/// </summary>/// <returns>后序遍历序列</returns>public string PostOrderTraversal(){_orderString = string.Empty;PostOrder(Root);return _orderString.Trim();}/// <summary>/// 得到层次遍历序列/// </summary>/// <returns>层次遍历序列</returns>public string LevelTraversal(){_orderString = string.Empty;if (Root != null){LinkQueue<BinTreeNode<T>> lq = new LinkQueue<BinTreeNode<T>>();lq.EnQueue(Root);while (lq.IsEmpty() == false){BinTreeNode<T> temp = lq.QueueFront;lq.DeQueue();_orderString += temp.Data + " ";if (temp.LeftChild != null)lq.EnQueue(temp.LeftChild);if (temp.RightChild != null)lq.EnQueue(temp.RightChild);}}return _orderString.Trim();}/// <summary>/// 从current结点开始寻找find结点的父亲结点的递归函数/// </summary>/// <param name="current">开始递归的根结点</param>/// <param name="find">要寻找的结点</param>/// <returns>find结点的父亲结点</returns>private BinTreeNode<T> FindParent(BinTreeNode<T> current, BinTreeNode<T> find){if (find == null)throw new ArgumentNullException();if (current == null)return null;if (current.LeftChild != null && current.LeftChild.Equals(find))return current;if (current.RightChild != null && current.RightChild.Equals(find))return current;BinTreeNode<T> temp = FindParent(current.LeftChild, find);if (temp != null)return temp;return FindParent(current.RightChild, find);}/// <summary>/// 得到find结点的父亲结点,若不存在返回null./// </summary>/// <param name="find">要寻找的结点</param>/// <returns>该结点的父亲结点</returns>public BinTreeNode<T> GetParent(BinTreeNode<T> find){if (find == null)throw new ArgumentNullException();return FindParent(Root, find);}/// <summary>/// 得到当前结点的左兄弟结点,若不存在返回null./// </summary>/// <param name="current">当前结点</param>/// <returns>当前结点的左兄弟结点</returns>public BinTreeNode<T> GetLeftSibling(BinTreeNode<T> current){if (current == null)throw new ArgumentNullException();BinTreeNode<T> parent = GetParent(current);if (parent != null && parent.LeftChild != null && parent.LeftChild.Equals(current) == false)return parent.LeftChild;return null;}/// <summary>/// 得到当前结点的右兄弟结点,若不存在返回null./// </summary>/// <param name="current">当前结点</param>/// <returns>当前结点的右兄弟结点</returns>public BinTreeNode<T> GetRightSibling(BinTreeNode<T> current){if (current == null)throw new ArgumentNullException();BinTreeNode<T> parent = GetParent(current);if (parent != null && parent.RightChild != null && parent.RightChild.Equals(current) == false)return parent.RightChild;return null;}/// <summary>/// 删除以current为根的子树/// </summary>/// <param name="current">要删除子树的根</param>public void DeleteSubTree(BinTreeNode<T> current){if (current == null)throw new ArgumentNullException();if (Root == null)throw new Exception("二叉树为null.");if (Root.Equals(current)){Root = null;}else{BinTreeNode<T> parent = GetParent(current);if (parent != null && parent.LeftChild != null && parent.LeftChild.Equals(current))parent.LeftChild = null;if (parent != null && parent.RightChild != null && parent.RightChild.Equals(current))parent.RightChild = null;}}/// <summary>/// 寻找结点的递归函数/// </summary>/// <param name="current">开始结点</param>/// <param name="data">数据</param>/// <returns>数据所在的结点</returns>private BinTreeNode<T> FindData(BinTreeNode<T> current, T data){if (data == null)throw new ArgumentNullException();if (current == null)return null;if (current.Data.CompareTo(data) == 0)return current;BinTreeNode<T> temp = FindData(current.LeftChild, data);if (temp != null)return temp;return FindData(current.RightChild, data);}/// <summary>/// 根据数据的值找到二叉树中对应的结点,若不存在返回null./// </summary>/// <param name="data">数据的值</param>/// <returns>二叉树中对应的结点</returns>public BinTreeNode<T> Search(T data){if (data == null)throw new ArgumentNullException();return FindData(Root, data);}/// <summary>/// 统计叶子结点个数的递归函数/// </summary>/// <param name="current">统计叶子结点子树的根</param>/// <param name="count">叶子结点的个数</param>private void FindLeafCount(BinTreeNode<T> current, ref int count){if (current == null)return;if (current.LeftChild == null && current.RightChild == null){count++;return;}FindLeafCount(current.LeftChild, ref count);FindLeafCount(current.RightChild, ref count);}/// <summary>/// 得到该树叶子结点的个数/// </summary>/// <returns>叶子结点的个数</returns>public int GetLeafCount(){int count = 0;FindLeafCount(Root, ref count);return count;}/// <summary>/// 交换左右子树的递归函数/// </summary>/// <param name="current">子树的根结点</param>private void Exchange(BinTreeNode<T> current){if (current == null)return;if (current.LeftChild != null || current.RightChild != null){BinTreeNode<T> temp = current.LeftChild;current.LeftChild = current.RightChild;current.RightChild = temp;}if (current.LeftChild != null)Exchange(current.LeftChild);if (current.RightChild != null)Exchange(current.RightChild);}/// <summary>/// 交换二叉树的左右子树/// </summary>public void Exchange(){Exchange(Root);}}
}
例子:
class Program
{static void Main(string[] args){BinTreeNode<string> a = new BinTreeNode<string>("A");BinTreeNode<string> b = new BinTreeNode<string>("B");BinTreeNode<string> c = new BinTreeNode<string>("C");BinTreeNode<string> d = new BinTreeNode<string>("D");BinTree<string> bintree = new BinTree<string>(a);bintree.Insert(a, b, c);bintree.Insert(b, d, null);Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());// 前序遍历:A B D CConsole.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());// 中序遍历:D B A CConsole.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());// 后序遍历:D B C AConsole.WriteLine("层次遍历:{0}", bintree.LevelTraversal());// 层次遍历:A B C DBinTreeNode<string> parent = bintree.GetParent(d);BinTreeNode<string> lSibling = bintree.GetLeftSibling(c);BinTreeNode<string> rSibling = bintree.GetRightSibling(b);if (parent != null)Console.WriteLine("结点{0}的Parent结点:{1}", d.Data, parent.Data);elseConsole.WriteLine("结点{0}无Parent.", d.Data);// 结点D的Parent结点:Bif (lSibling != null)Console.WriteLine("结点{0}的左兄弟结点:{1}", c.Data, lSibling.Data);elseConsole.WriteLine("结点{0}无左兄弟结点.", c.Data);// 结点C的左兄弟结点:Bif (lSibling != null)Console.WriteLine("结点{0}的右兄弟结点:{1}", b.Data, rSibling.Data);elseConsole.WriteLine("结点{0}无右兄弟结点.", b.Data);// 结点B的右兄弟结点:Cbintree.DeleteSubTree(d);Console.WriteLine("把结点{0}从二叉树中移除.", d.Data);// 把结点D从二叉树中移除.Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());// 前序遍历: A B CConsole.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());// 中序遍历:B A C Console.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());// 后序遍历: B C A Console.WriteLine("层次遍历:{0}", bintree.LevelTraversal());// 层次遍历: A B CBinTreeNode<string> e = bintree.Search("A");if (e != null && e.LeftChild != null)Console.WriteLine("寻找结点{0}的左孩子为{1}", e.Data, e.LeftChild.Data);elseConsole.WriteLine("未找到{0}结点或者{0}结点左孩子为null", a.Data);// 寻找结点A的左孩子为BConsole.WriteLine("叶子结点的个数:{0}", bintree.GetLeafCount());// 叶子结点的个数:2bintree.Exchange();Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());// 前序遍历:A C BConsole.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());// 中序遍历: C A B Console.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());// 后序遍历: C B A Console.WriteLine("层次遍历:{0}", bintree.LevelTraversal());// 层次遍历: A C B}
}
3. 树与森林
3.1 树的存储
(1)顺序存储
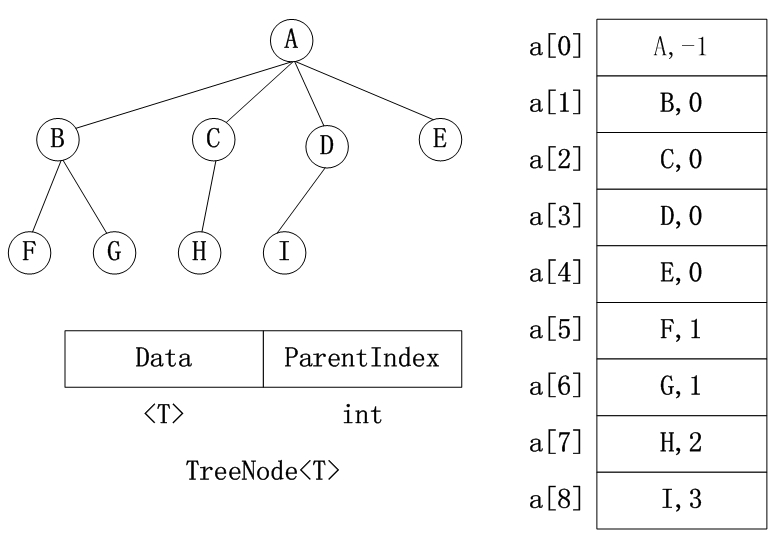
(2)链式存储
A. 存储双亲结点
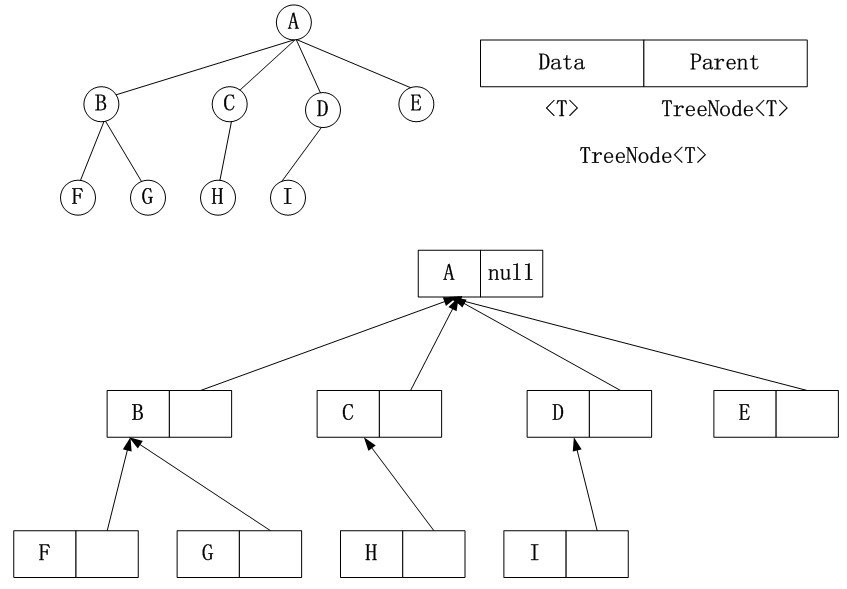
B. 存储孩子结点
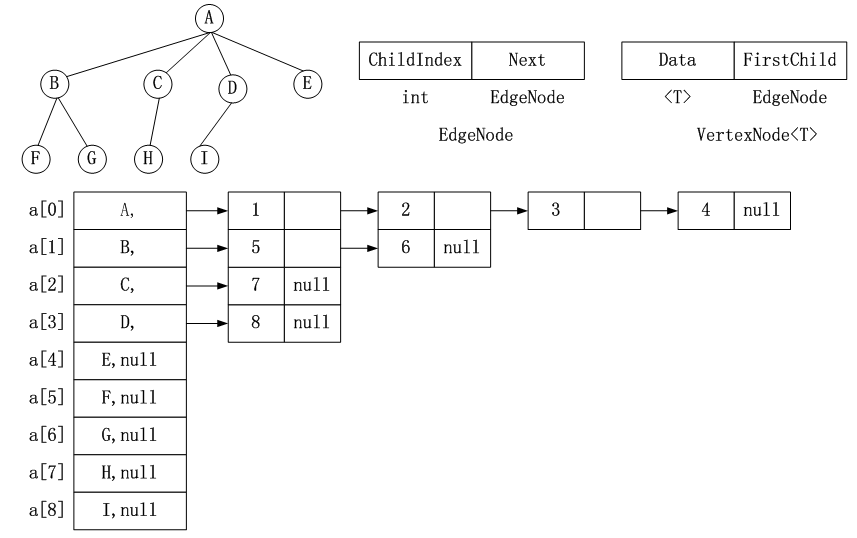
C. 存储孩子和兄弟结点
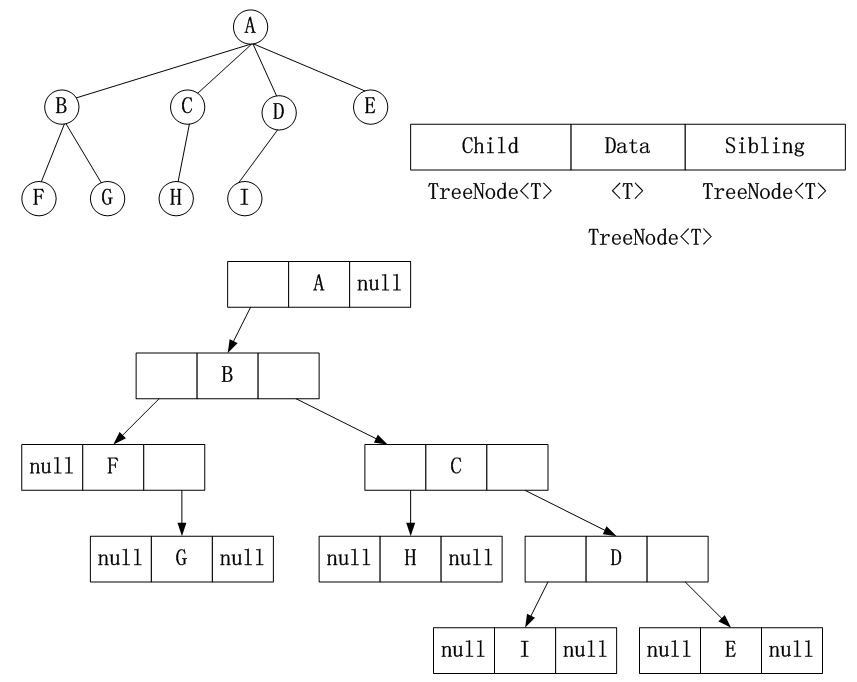
3.2 树与二叉树的相互转换
(1)树转换成二叉树
按照左孩子,右兄弟规则。
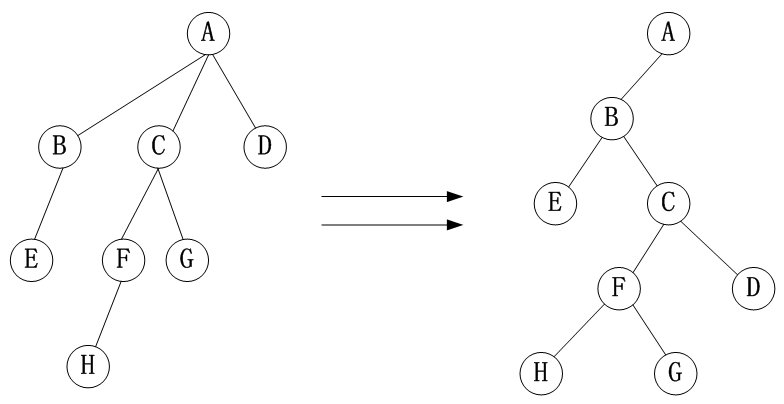
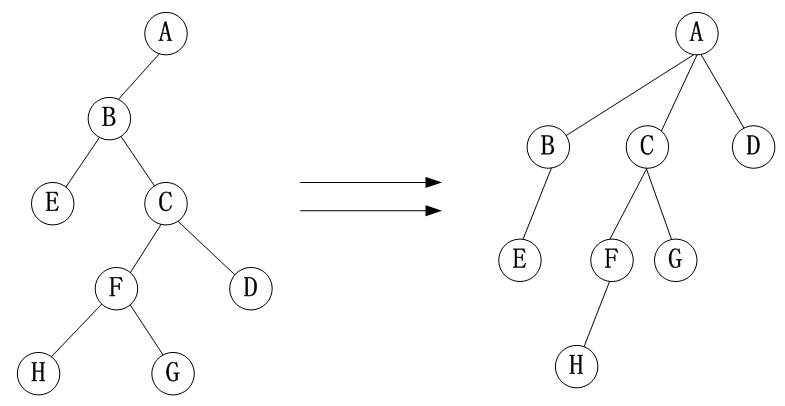
(2)二叉树转换成树
按照左孩子,右兄弟规则的逆过程。
3.3 森林与二叉树的相互转换
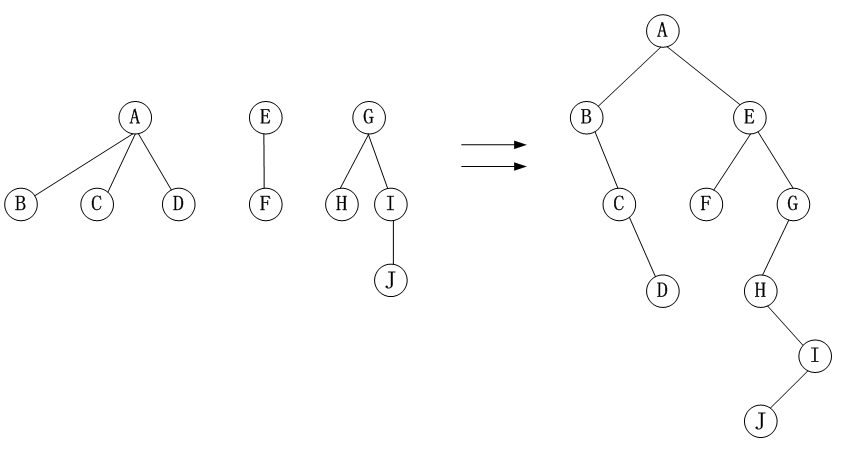
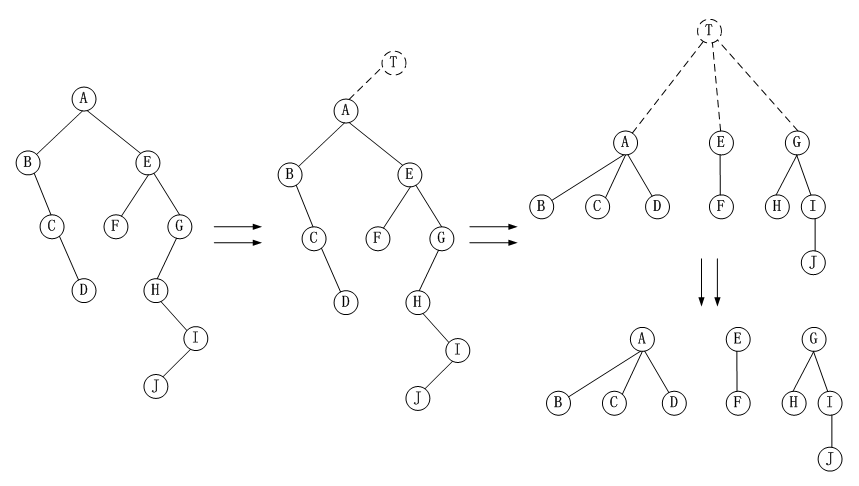
(1)森林转化成二叉树
设F=(T1,T2,⋯,Tn)F=(T_1,T_2,\cdots,T_n)F=(T1,T2,⋯,Tn)为树T1,T2,⋯,TnT_1,T_2,\cdots,T_nT1,T2,⋯,Tn组成的森林,B(F)B(F)B(F)为其对应的二叉树。
- 若n=0n=0n=0,则B(F)=ϕB(F)=\phiB(F)=ϕ。
- 若n>0n>0n>0,`B(F)B(F)B(F)的根为Root(T1)Root(T_1)Root(T1),B(F)B(F)B(F)的左子树由T1T_1T1的诸子树组成,右子树由B({T2,⋯,Tn})B(\lbrace T_2,\cdots,T_n\rbrace)B({T2,⋯,Tn})组成。
方式1:
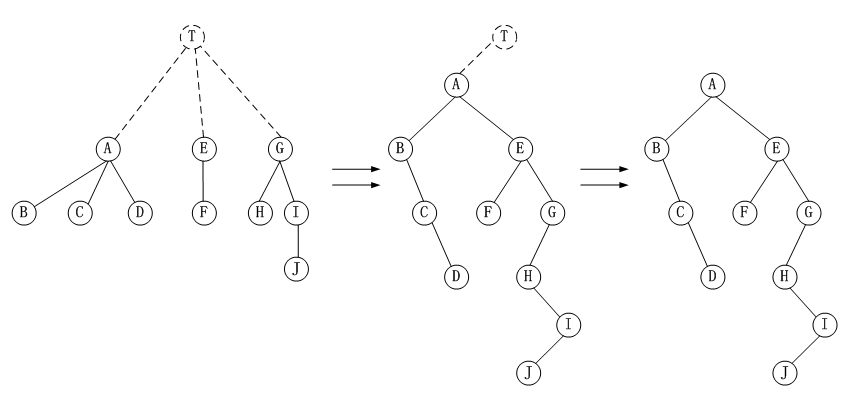
方式2:
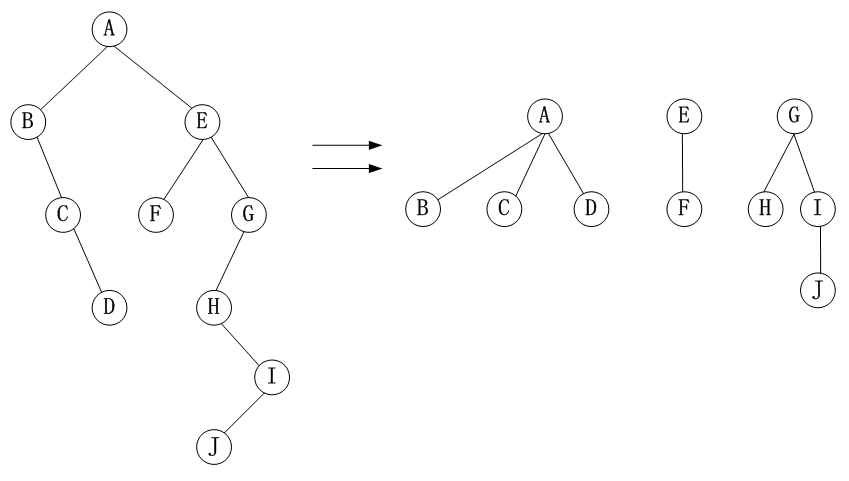
(2)二叉树转化成森林
设B=(Root,LB,RB)B=(Root,LB,RB)B=(Root,LB,RB)是一颗二叉树,F(B)={T1,T2,⋯,Tn}F(B)=\lbrace T_1,T_2,\cdots,T_n \rbraceF(B)={T1,T2,⋯,Tn}为其对应的森林。
- 若B=ϕB=\phiB=ϕ,则F(B)=ϕF(B)=\phiF(B)=ϕ (n=0)(n=0)(n=0)。
- 若BBB不等于ϕ\phiϕ,则T1T_1T1的根为二叉树BBB的根RootRootRoot,T1T_1T1的子树森林由BBB的左子树LBLBLB转换而成,其余树组成的森林F(T)={T2,⋯,Tn}F(T)=\lbrace T_2,\cdots,T_n \rbraceF(T)={T2,⋯,Tn}由BBB的右子树RBRBRB转换而成。
方式1:
方式2:
3.4 树与森林的遍历
(1)树的遍历
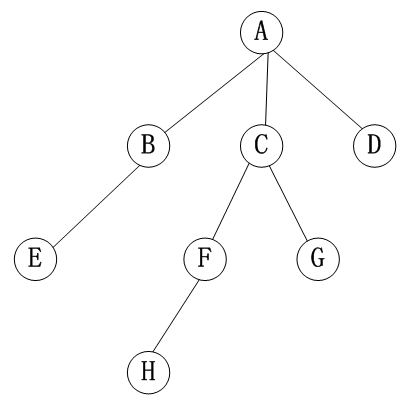
前序遍历:首先访问根结点;然后前序遍历每棵子树。
- 前序遍历序列:A B E C F H G D
后序遍历:首先后序遍历每棵子树;然后访问根结点。
- 后序遍历序列:E B H F G C D A
(2)森林的遍历
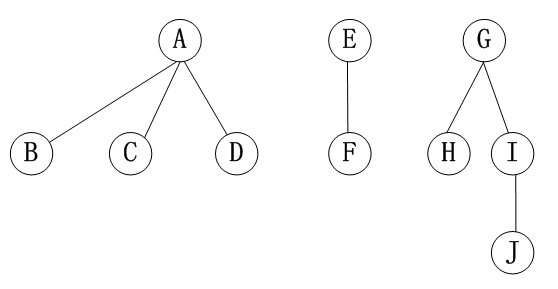
前序遍历:首先访问第一棵树的根结点;然后前序遍历第一棵树的子树;再前序遍历由其余树组成的森林。
- 前序遍历序列:A B C D E F G H I J
后序遍历:先后序遍历第一棵树的子树;然后访问第一棵树的根结点;再后序遍历由其余树组成的森林。
- 后序遍历序列:B C D A F E H J I G
4. 线索二叉树
4.1 引入
性质:设二叉树利用二叉链表存储且结点个数为nnn,则该二叉树的链域个数为2n2n2n,空链域个数为n+1n+1n+1。
想法:利用空链域存储该树按照某种方式遍历(前序、中序、后序)的前趋或后继结点。
结构:
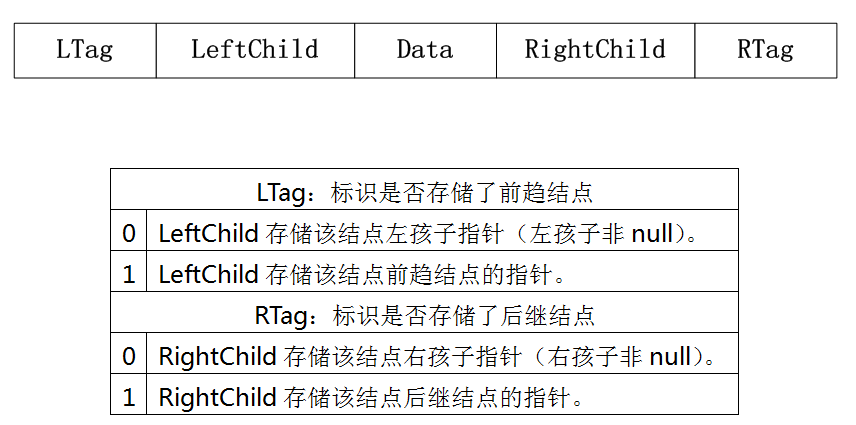
4.2 相关概念
线索:在这种结构中指向其前趋或后继结点的指针。
线索二叉树:加上线索的二叉树。
线索化:把二叉树变成线索二叉树的过程。
线索化的方式:前序线索化、中序线索化、后序线索化
例子:中序线索化
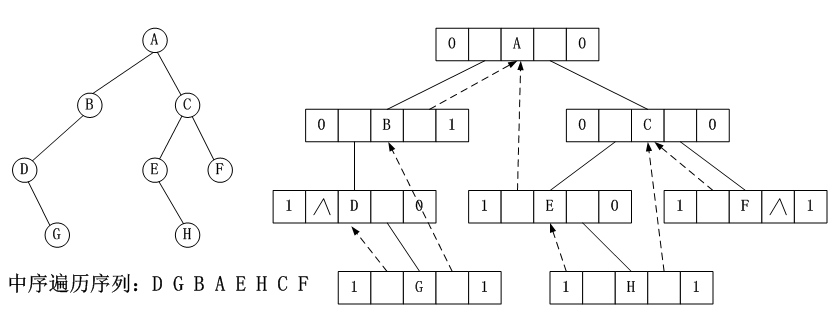
例子:前序线索化
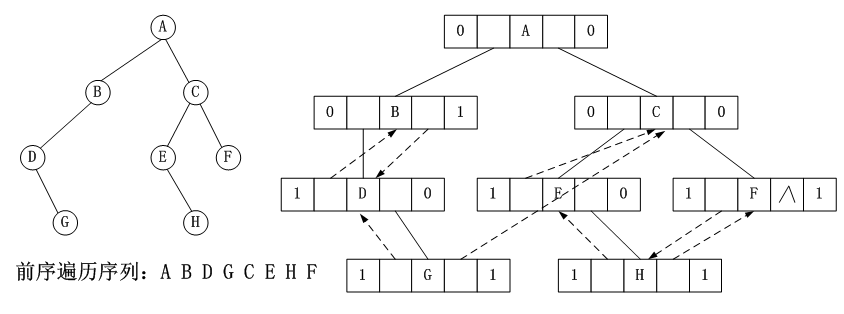
5. 哈夫曼树及其编码(Huffman)
5.1 哈夫曼树的定义
路径:连接两个结点的分支,构成这两个结点的路径。
路径长度:两个结点路径上的分支数。
结点的权:为结点赋的一个有意义的实数。
结点的带权路径长度:根结点到该结点的路径长度与该结点权值的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。记为:WPL=∑i=1nωiLiWPL=\sum_{i=1}^{n}\omega_iL_iWPL=∑i=1nωiLi,nnn为叶子结点的个数。
哈夫曼树:nnn个带权叶子结点构成的所有二叉树中,带权路径长度WPLWPLWPL最小的二叉树。(最优二叉树)
5.2 哈夫曼树的构造
第1步:根据给定的nnn个权值ω1,ω2,⋯,ωn\omega_1,\omega_2,\cdots,\omega_nω1,ω2,⋯,ωn,构成nnn棵二叉树的森林F={T1,T2,⋯,Tn}F=\lbrace T_1,T_2,\cdots,T_n \rbraceF={T1,T2,⋯,Tn},其中每棵二叉树TiT_iTi中都只有一个权值`ωi\omega_iωi的根结点,其左右子树均为空。
第2步:在森林FFF中选出两棵根结点权值最小的树作为一棵新树的左右子树,且置新树的根结点的权值为其左右子树上根结点的权值之和。
第3步:从FFF中删除构成新树的哪两棵树,同时把新树加入FFF中。
第4步:重复第2和3步,直到FFF中只含有一棵树为止,此树便是Huffman树。
例子:给定权集ω={2,3,4,7,8,9}\omega=\lbrace 2,3,4,7,8,9 \rbraceω={2,3,4,7,8,9} ,试构造关于ω\omegaω的一颗哈夫曼树,并求其带权路径长度 。
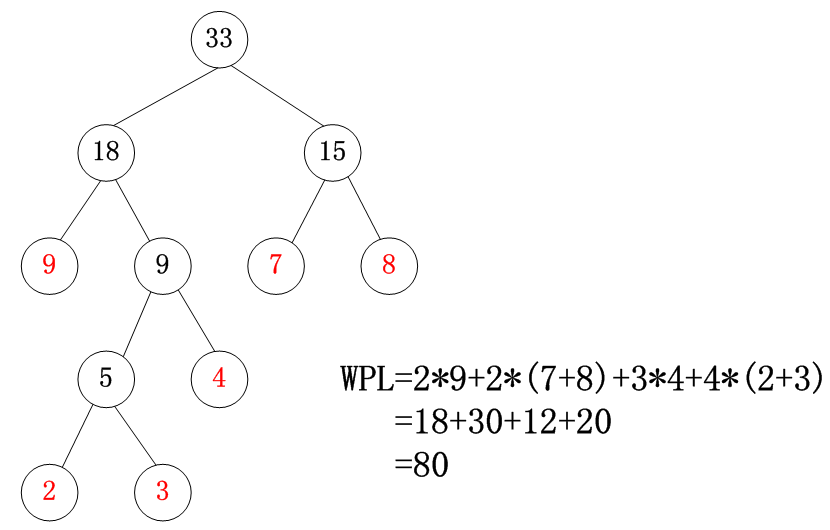
5.3 哈夫曼编码的概念
前缀码规则:对字符集编码时,字符集中任一字符的编码都不是其它字符编码的前缀。
例子:
A:0 B:00 C:01 D:10(违反前缀码规则)
000010 BBD、AAAAD、BAAD、AABD (不唯一,解码时有二义性)
A:00 B:01 C:10 D:11(满足前缀码规则)
000010 AAC (唯一)
哈夫曼编码:将哈夫曼树中,每个分支结点的左分支标0,右分支标1,把从根结点到每个叶子结点的路径上的标号连接起来作为该叶子结点所代表符号的编码,这样得到的编码称为Huffman编码。(优点:满足前缀码规则)
例子:对所要发送的数据进行二进制编码。
state,seat,act,tea,cat,set,a,eat
第一种编码方式:
's':"000” 't':“001” 'a':“010” 'e':“011” 'c':“100” ',':“110”
此种编码满足前缀码规则,但编码过长。eat:011010001
第二种编码方式:
统计字符出现的频数:‘s’:3 ‘t’:8 ‘a’:7 ‘e’:5 ‘c’:2 ‘,’:7
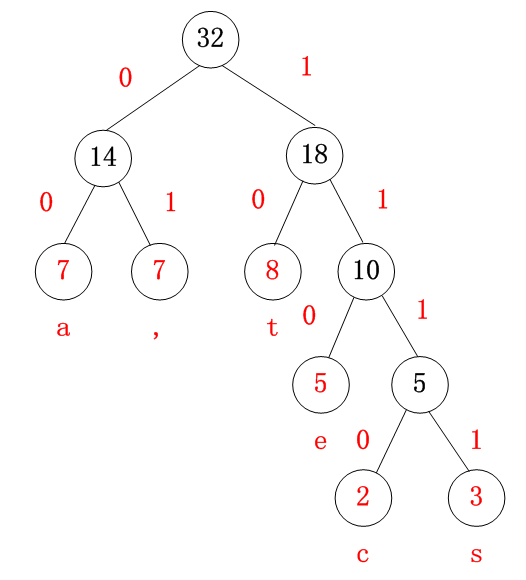
'a':"00” ',':“01” 't':“10” 'e':“110” 'c':“1110” 's':“1111”
- eat:1100010
- state:1111100010110
- seat:11111100010
5.4 哈夫曼编码的实现
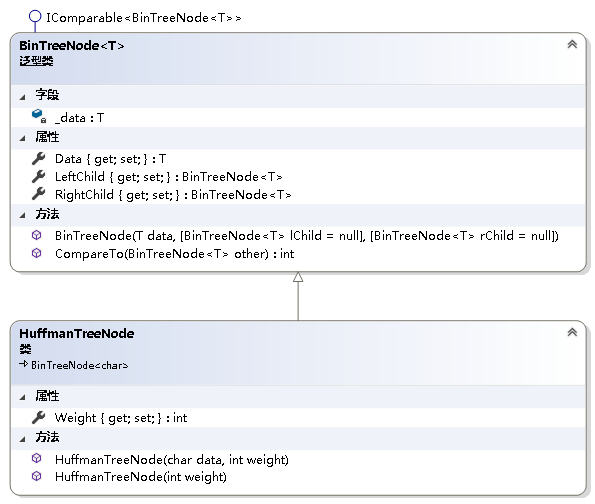
namespace NonLinearStruct
{/// <summary>/// 表示Huffman树的结点/// </summary>public class HuffmanTreeNode : BinTreeNode<char>{/// <summary>/// 结点的权值/// </summary>public int Weight { get; set; }/// <summary>/// 叶子结点 -- 字符/// </summary>/// <param name="data">字符</param>/// <param name="weight">结点的权</param>public HuffmanTreeNode(char data, int weight) : base(data){Weight = weight;}/// <summary>/// 其它结点/// </summary>/// <param name="weight">结点的权</param>public HuffmanTreeNode(int weight) : base('\0'){Weight = weight;}}
}

namespace NonLinearStruct
{/// <summary>/// Huffman字典/// </summary>public class HuffmanDicItem{/// <summary>/// 获取或设置字符/// </summary>public char Character { get; set; }/// <summary>/// 获取或设置编码/// </summary>public string Code { get; set; }/// <summary>/// 构造函数/// </summary>/// <param name="charactor">字符</param>/// <param name="code">编码</param>public HuffmanDicItem(char charactor, string code){Character = charactor;Code = code;}}
}
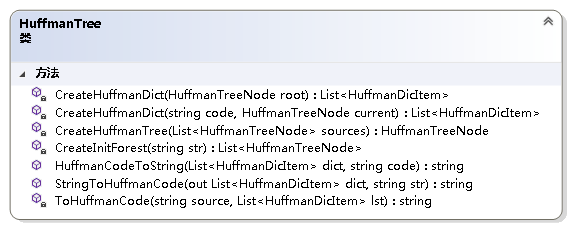
using System;
using System.Collections.Generic;
using System.Linq;
namespace NonLinearStruct
{/// <summary>/// Huffman树/// </summary>public class HuffmanTree{/// <summary>/// 构造Huffman树初始的森林/// </summary>/// <param name="str">字符串</param>/// <returns>结点的集合,构成初始的森林</returns>private List<HuffmanTreeNode> CreateInitForest(string str){if (string.IsNullOrEmpty(str))throw new ArgumentNullException();List<HuffmanTreeNode> result = new List<HuffmanTreeNode>();char[] charArray = str.ToCharArray();List<IGrouping<char, char>> lst = charArray.GroupBy(a => a).ToList();foreach (IGrouping<char, char> g in lst){char data = g.Key;int weight = g.ToList().Count;HuffmanTreeNode node = new HuffmanTreeNode(data, weight);result.Add(node);}return result;}/// <summary>/// 构造Huffman树/// </summary>/// <param name="sources">初始的结点的集合</param>/// <returns>Huffman树的Root</returns>private HuffmanTreeNode CreateHuffmanTree(List<HuffmanTreeNode> sources){if (sources == null)throw new ArgumentNullException();if (sources.Count < 2)throw new ArgumentException("构造Huffman树,最少为2个结点。");HuffmanTreeNode root = default(HuffmanTreeNode);bool isNext = true;while (isNext){List<HuffmanTreeNode> lst = sources.OrderBy(a => a.Weight).ToList();HuffmanTreeNode n1 = lst[0];HuffmanTreeNode n2 = lst[1];int weight = n1.Weight + n2.Weight;HuffmanTreeNode node = new HuffmanTreeNode(weight);node.LeftChild = n1;node.RightChild = n2;if (lst.Count == 2){root = node;isNext = false;}else{sources = lst.GetRange(2, lst.Count - 2);sources.Add(node);}}return root;}/// <summary>/// 创建Huffman编码的字典/// </summary>/// <param name="code"></param>/// <param name="current"></param>/// <returns></returns>private List<HuffmanDicItem> CreateHuffmanDict(string code, HuffmanTreeNode current){if (current == null)throw new ArgumentNullException();List<HuffmanDicItem> result = new List<HuffmanDicItem>();if (current.LeftChild == null && current.RightChild == null){result.Add(new HuffmanDicItem(current.Data, code));}else{List<HuffmanDicItem> dictL = CreateHuffmanDict(code + "0",(HuffmanTreeNode)current.LeftChild);List<HuffmanDicItem> dictR = CreateHuffmanDict(code + "1",(HuffmanTreeNode)current.RightChild);result.AddRange(dictL);result.AddRange(dictR);}return result;}/// <summary>/// 创建Huffman编码的字典/// </summary>/// <param name="root">Huffman树</param>/// <returns>Huffman字典</returns>private List<HuffmanDicItem> CreateHuffmanDict(HuffmanTreeNode root){if (root == null)throw new ArgumentNullException();return CreateHuffmanDict(string.Empty, root);}/// <summary>/// 对字符串进行编码/// </summary>/// <param name="dict">Huffman字典</param>/// <param name="str">编码字符串</param>/// <returns>编码后的字符串</returns>public string StringToHuffmanCode(out List<HuffmanDicItem> dict, string str){List<HuffmanTreeNode> forest = CreateInitForest(str);HuffmanTreeNode root = CreateHuffmanTree(forest);dict = CreateHuffmanDict(root);string result = ToHuffmanCode(str, dict);return result;}/// <summary>/// 给定Huffman字典对编码进行解码/// </summary>/// <param name="dict">Huffman字典</param>/// <param name="code">解码的字符</param>/// <returns>解码后的字符</returns>public string HuffmanCodeToString(List<HuffmanDicItem> dict, string code){string result = string.Empty;for (int i = 0; i < code.Length;){foreach (HuffmanDicItem item in dict){if (code[i] == item.Code[0] && item.Code.Length + i <= code.Length){string temp = code.Substring(i, item.Code.Length);if (temp == item.Code){result += item.Character;i += item.Code.Length;break;}}}}return result;}/// <summary>/// 利用Huffman字典对字符集进行编码/// </summary>/// <param name="source">编码的字符</param>/// <param name="lst">Huffman字典</param>/// <returns>编码后的字符串</returns>private string ToHuffmanCode(string source, List<HuffmanDicItem> lst){if (string.IsNullOrEmpty(source))throw new ArgumentNullException();if (lst == null)throw new ArgumentNullException();string result = string.Empty;for (int i = 0; i < source.Length; i++){result += lst.Single(a => a.Character == source[i]).Code;}return result;}}
}
客户端代码:
class Program
{static void Main(string[] args){string str = "state,seat,act,tea,cat,set,a,eat";Console.WriteLine(str);// state,seat,act,tea,cat,set,a,eatHuffmanTree huffmanTree = new HuffmanTree();List<HuffmanDicItem> dic;string huffmanCode = huffmanTree.StringToHuffmanCode(out dic, str);string temp = string.Empty;for (int i = 0; i < dic.Count; i++){temp += @"'" + dic[i].Character + "':" + "\"" + dic[i].Code + "\"\r\n";}Console.WriteLine(temp.Substring(0, temp.Length - 2));// 'a':"00"// ',':"01"// 't':"10"// 'e':"110"// 'c':"1110"// 's':"1111"Console.WriteLine(huffmanCode);// 1111100010110011111110001001001110100110110000111100010011111110100100011100010string decode = huffmanTree.HuffmanCodeToString(dic, huffmanCode);Console.WriteLine(decode);//state,seat,act,tea,cat,set,a,eat}
}

相关文章:

【as3】键盘事件
在AS3中,键盘事件是由KeyboardEvent类来处理的,属于flash.events包里面,有两种类型的键盘事件:KeyboardEvent.KEY_DOWN 和 KeyboardEvent.KEY_UP,对于键的代码获得我们通过keyCode这个属性 其实键盘事件使用起来还是相…

在后台代码中引入XAML的方法
本文将介绍三种方法用于在后台代码中动态加载XAML,其中有两种方法是加载已存在的XAML文件,一种方法是将包含XAML代码的字符串转换为WPF的对象。 这些是我在编写RegeX时获得的经验,它们将会给WPF程序带来更多的灵活性。 一、在资源字典中载入项…

JavaScript面向对象怎样删除标签页?
单击小标签右上角的按钮可D头删除标签页。其开发思路是,为“x”元素绑定单击事件,事件触发后,通过父元素1i获取索弓引值,然后用这个索引值将对应的li和section删除,并在删除后更新标签页的选中效电下面我们们就开始进行…

数据结构与算法:16 Leetcode同步练习(六)
Leetcode同步练习(六) 目录 题目01:相同的树题目02:对称二叉树题目03:二叉树的最大深度题目04: Pow(x, n)题目05:子集题目06:格雷编码题目07:二叉树的最近公共祖先题目…

Apache启动时报Could not reliably determine the server's fully qualified domain name
在系统启动时apache,没有启动起来,查看“事件查看器”发现报一些错误: The Apache service named reported the following error:>>> httpd.exe: Could not reliably determine the servers fully qualified domain name, using 19…

Windows Phone SDK update for Windows Phone 7.8
下载:http://www.microsoft.com/en-us/download/details.aspx?id36474 (在线安装) http://kuai.xunlei.com/d/cHbJCAIX4wBNVgFR5aa (离线下载 全语言 5.5G....) MS博客介绍:http://blogs.windows.com/windows_phone/b/wpdev/archive/2013/01/22/now-a…

作为一名合格的前端开发工程师需要会哪些
作为一名合格的前端开发工程师需要会哪些?web前端要学习的内容有很多,想要成为一名合格的web前端工程师,综合实力是要非常强的,来看看下面的详细介绍吧。 作为一名合格的前端开发工程师需要会哪些?前端开发工程师不仅要掌握基本的前端开发技…
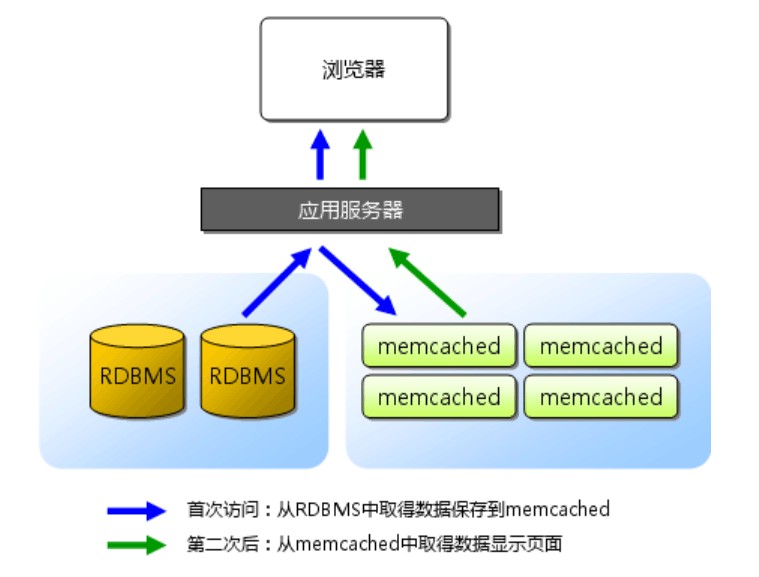
memcached部署
第1章 memcached 1 memcached前言 1.1 memcached诞生的原因 2003年诞生了memcached Web1.0 2005以前 企业提供内容为主。 Web2.02005-2012 企业只提供平台,用户参与上传下载内容。 memcached 内存缓存软件,内存比磁盘快。 传统场景中,多数…

线性代数:第二章 矩阵及其运算
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍有关矩阵的知识,主要包括矩阵的基本运算(加法、数乘、乘法、乘幂、…

sdut 2401 最大矩形面积
1http://acm.sdut.edu.cn/sdutoj/problem.php?actionshowproblem&problemid2401 /*2 最大矩形面积,把边界点加上3 从左往右 处理一遍;4 再从上往下处理一遍;5 */6 7 #include<stdio.h>8 #define maxn 200009 #include<cmath>…
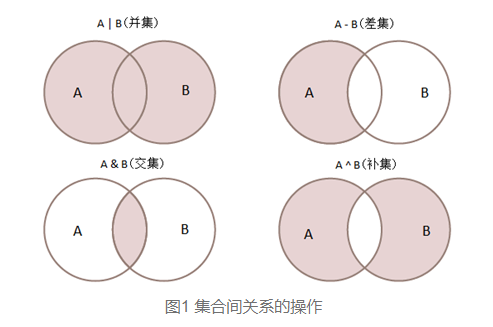
Python中怎样改变集合之间的关系?
Python中怎样改变集合之间的关系?数学中,两个集合关系的常见操作包括:交集、并集、差集、补集。设A,B是两个集合,集合关系的操作介绍如下: 交集是指属于集合A且属于集合B的元素所组成的集合, 并集是指集合…
数据结构与算法:17 图
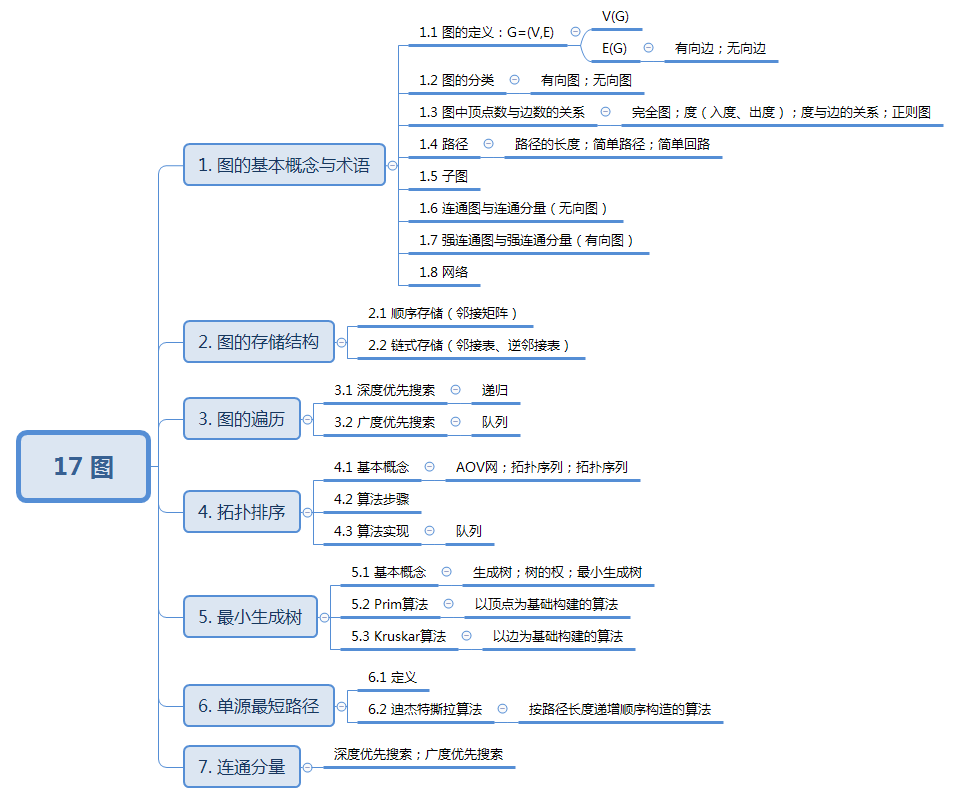
17 图 知识结构: 1. 图的基本概念与术语 1.1 图的定义 图由顶点集和边集组成,记为G(V,E)G(V,E)G(V,E)。 顶点集:顶点的有穷非空集合,记为V(G)V(G)V(G)。边集:顶点偶对的有穷集合,记为E(G)E(G)E(G) 。 …

云计算安全:技术与应用
云计算安全:技术与应用中国电信网络安全实验室 编著ISBN 978-7-121-14409-72012年1月出版定价:59.00元16开236页宣传语:全面了解云计算安全风险、安全防护手段的佳作!内 容 简 介随着云计算的兴起,安全成为云计算能否顺…

再谈HOST文件
前几天弄了一个关于禁止打开某个网站的文章后,觉得这个HOST文件真的挺有意思的。并且也总是想把自己对它新的理解写下来(也许大家都明白了)以下是HOST文件的内容:# Copyright (c) 1993-1999 Microsoft Corp.## This is a sample H…

PMP®考试是什么机构
项目管理对于很多职场中的人来说是以后要发展的一个方向,随着各职业内卷也越来越严重,pmp认证引起了大家的关注,有朋友问:PMP考试是什么机构?下面我们给大家介绍一下。 PMP考试是什么机构?PMP考试认证在我国大陆地区需要三方机构…
技术图文:03 结构型设计模式(上)
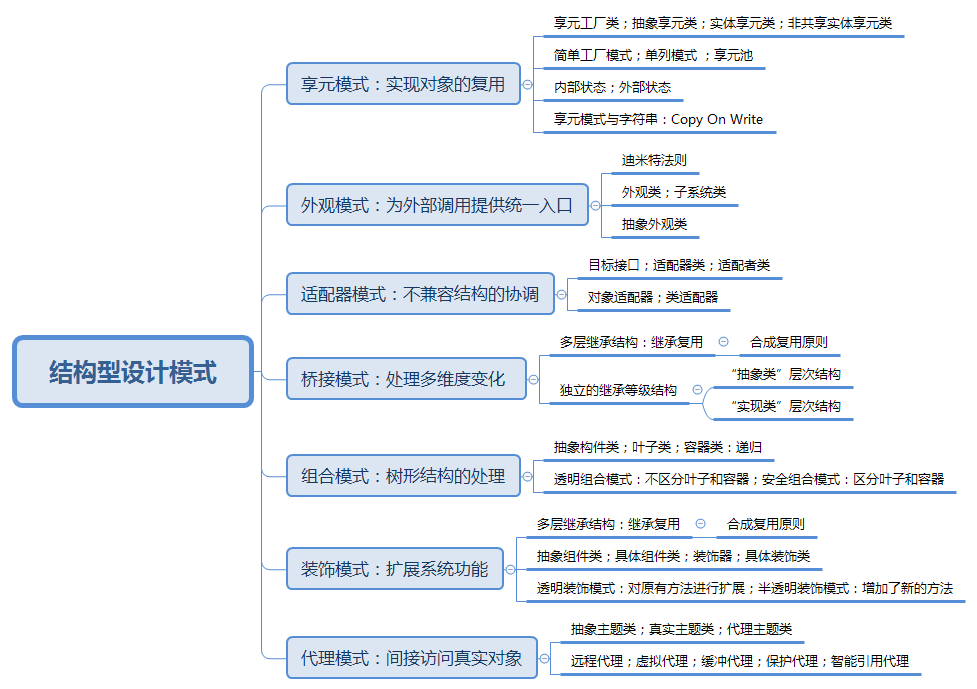
结构型设计模式(上) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 享元模式 – 实现对象的复用 Sunny 软件公司欲开发一个围棋软件,其界面效果如下图所示: 图2 围…

Linux抓包工具tcpdump详解
原文链接 tcpdump是一个用于截取网络分组,并输出分组内容的工具,简单说就是数据包抓包工具。tcpdump凭借强大的功能和灵活的截取策略,使其成为Linux系统下用于网络分析和问题排查的首选工具。 tcpdump提供了源代码,公开了接口&…

学习笔记TF065:TensorFlowOnSpark
2019独角兽企业重金招聘Python工程师标准>>> Hadoop生态大数据系统分为Yam、 HDFS、MapReduce计算框架。TensorFlow分布式相当于MapReduce计算框架,Kubernetes相当于Yam调度系统。TensorFlowOnSpark,利用远程直接内存访问(Remote Direct Memo…

HTML5培训好不好
HTML5培训好不好?这个问题,要看你选择的培训机构,想要学习HTML5技术,靠谱的培训机构非常重要,下面我们就来看看详细的介绍吧。 HTML5培训好不好?从前端开发的基础出发,学习使用HTML,CSS,JavaS…

技术图文:03 结构型设计模式(下)
结构型设计模式(下) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 组合模式 – 树形结构的处理 Sunny 软件公司欲开发一个杀毒(AntiVirus)软件,该软件…

程序员必知8大排序3大查找(三)
前两篇 《程序员必知8大排序3大查找(一)》 《程序员必知8大排序3大查找(二)》 三种查找算法:顺序查找,二分法查找(折半查找),分块查找,散列表(以后谈…
MongoDB给数据库创建用户
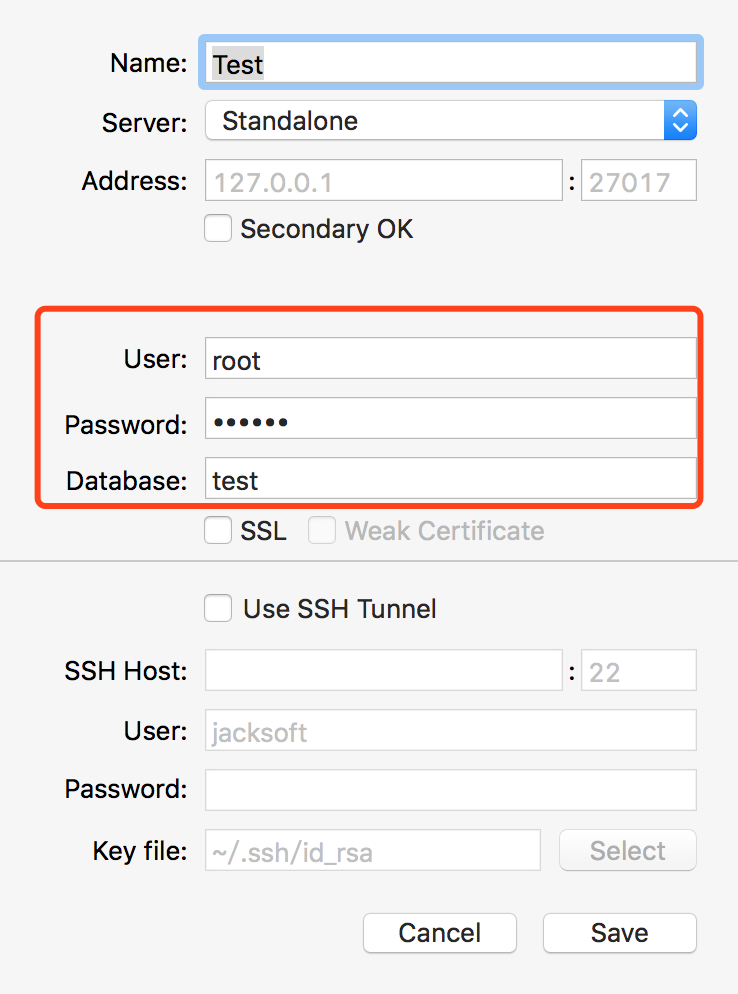
转自http://www.imooc.com/article/18439 一.先以非授权的模式启动MongoDB非授权: linux/Mac : mongod -f /mongodb/etc/mongo.confwindows : mongod --config c:\mongodb\etc\mongo.conf 或者 net start mongodb (前提是mongo安装到了服务里面ÿ…

如何挑选一家好的软件测试培训机构
随着智能时代的发展,我们的手机APP等各种软件都变得越来越复杂化、规模化,软件测试这一步骤是必不可少的,这也造就了这个行业的兴起,越来越多的人想要学习软件测试技术,想要知道如何挑选一家好的软件测试培训机构?来看…

POJ 3177 判决素数个数
时间限制: 1000ms内存限制:65536kB描述输入两个整数X和Y,输出两者之间的素数个数(包括X和Y)。输入两个整数X和Y,X和Y的大小任意。输出输出一个整数,结果可以是0,或大于0的整数。样例输入1 100样例输出25&am…

数据结构与算法:22 精选练习50
精选练习50 马上就要期末考试或者考研了。为了大家复习的方便,我精选了有关数据结构与算法的50道选择题,大家可以抽空练习一下。公众号后台回复“答案”可以获取该50道题目的答案。 01、数据在计算机中的表示称为数据的______。 (A&#x…

极速理解设计模式系列:11.单例模式(Singleton Pattern)
单例模式:确保某一个类只有一个实例,而且自行实例化并向整个系统提供这个实例。这个类称为单例类。 三要点: 一、单例类只能有一个实例 二、单例类必须自行创建自身实例 三、单例类自行向整个系统提供实例 类图: 应用场景…

参加web前端培训要学哪些知识
IT行业,web前端技术是比较吃香的,也是工资待遇非常高的行业之一,如果想要做一名合格的web前端工程师,系统学习是非常重要的,那么参加web前端培训要学哪些知识呢?来看看下面的详细介绍。 参加web前端培训要学哪些知识?…
数据结构与算法:19 排序
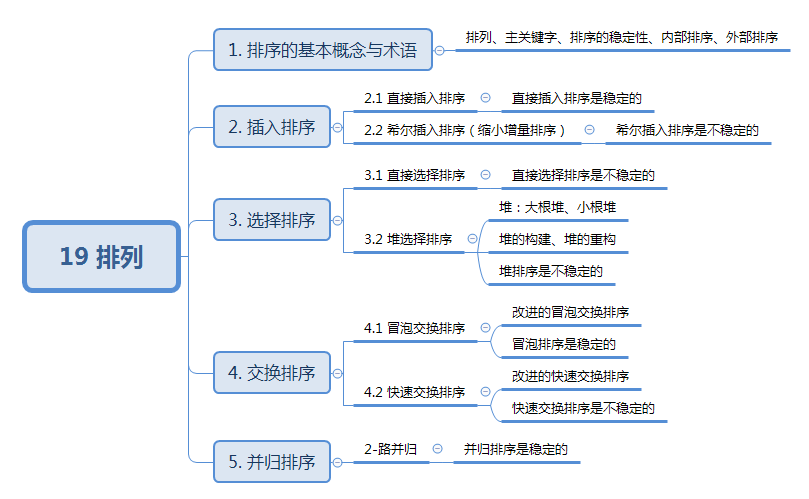
19 排序 知识结构: 1. 排序的基本概念与术语 假设含有nnn个记录的序列为{r1,r2,⋯,rn}\lbrace r_1,r_2,\cdots,r_n \rbrace{r1,r2,⋯,rn},其相应的关键字分别为{k1,k2,⋯,kn}\lbrace k_1,k_2,\cdots,k_n \rbrace{k1,k2,⋯,kn},…

Objective-C 什么是类
Objective-C 什么是类 转自http://www.189works.com/article-31219-1.html 之前一直做C开发,最近2个多月转 Objective-C, 入门的时候,遇到了很多的困惑。现在过节,正是解决他们的好时机。 主要参考来自http://www.sealiesoftware.…

APP之红点提醒三个阶段
下面这个页面就是我们进入APP后的主界面。客户选项的红点上数字就是显示我们没有查看的客户总数量。 当我们切换到客户这个fragment时,会显示贷款客户数量与保险客户数量。 当我们随便点击入一个选项,假如进入到保险客户的这个activity里面,L…
