hung-yi lee_p3_线性回归
文章目录
- 本节目的
- 解决过程
- 损失函数
- 解损失函数(by梯度下降)
- 改进模型
- 矫枉过正
- 解决方案
- 本课结论
本节目的
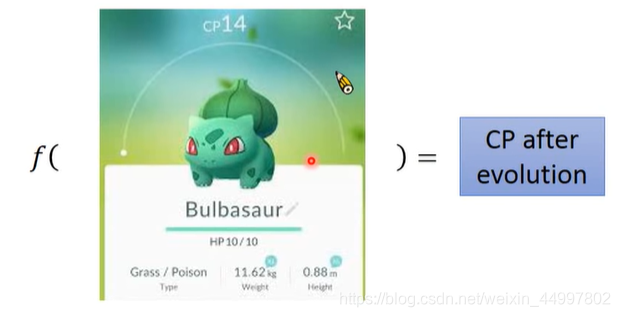
找到这样一个函数,输入宝可梦当前的CP(Combat Point)值,得到它进化后的CP值。
解决过程
损失函数
函数的函数:衡量一个函数的好坏(参数决定函数,即衡量一组参数的好坏),输出越大越不好

其中y加一个小尖帽是实际的数值

找一个f使得L(f)最小,能使L(f)最小的f记作f*,f对应的参数是w和b*。

这里用梯度下降来解左边的方程,注意,并不是梯度下降只有该用途。
解损失函数(by梯度下降)
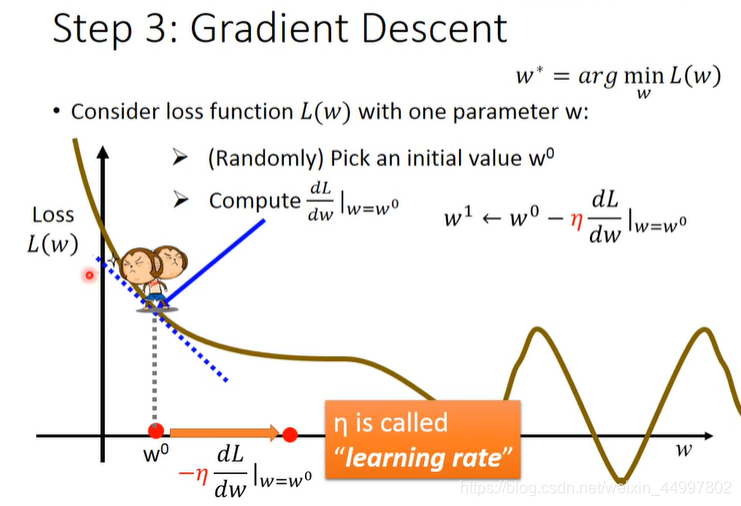
梯度下降的原理(以只有一个参数w的损失函数为例)
背景:暴力穷举的效率低,怎么办?
①选择一个w0作为起点(可以是随机可以不是)
②当前点的斜率是正的,则减小w;反之增加x(我们希望L(w)越小越好)
③具体增加或减少多少,取决于
i)现在的斜率绝对值,现在的斜率的绝对值越大,说明越陡峭,增量越大
ii)学习率 eta Learning rate越大,增量越大(学习速度快)
重复②③w0更新为w1,再更新为w2……(每次减去学习率×微分)
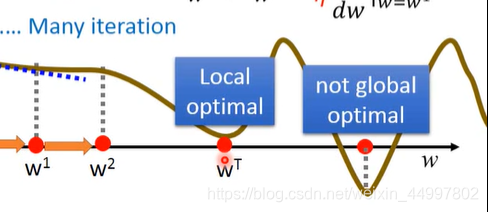
但是,解得的可能只是局部最小值,不是全局最小值。
不过这在回归当中不是个问题。下面考虑两个参数的损失函数。
原理一样,全微分变成偏微分。
梯度下降的梯度其实就是

更新参数过程

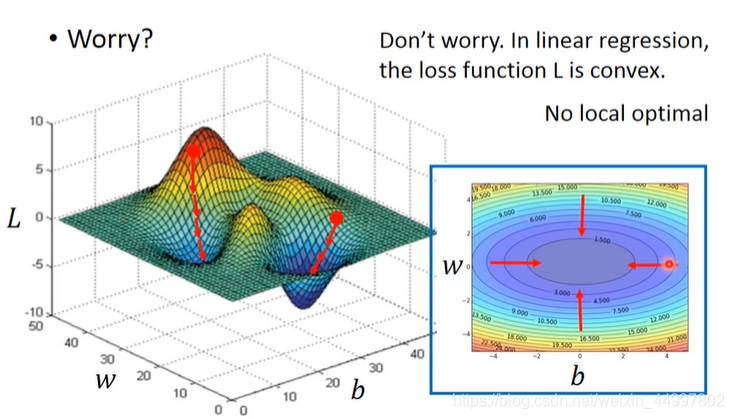
下面这幅图中颜色越冷表示损失函数的值越小。
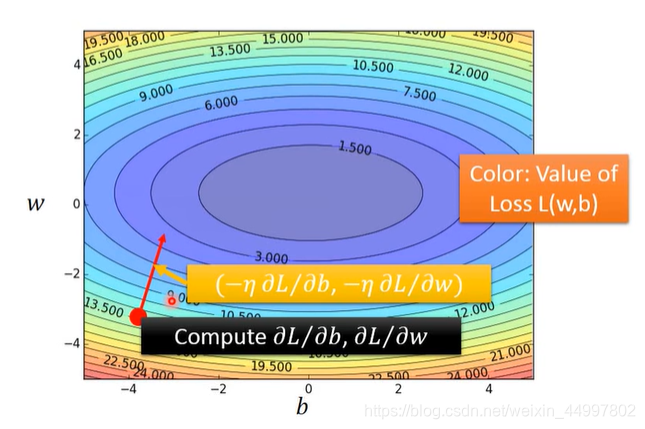
但是梯度下降方法似乎有个让人担心的地方——起点选的不对,也许会走的局部最小值点。但实际不会,因为这是个convex,没有局部最小值,随便从哪个起点开始,都会到全局最小值点。(左边是设想,右边是实际)
偏微分具体求法

结果
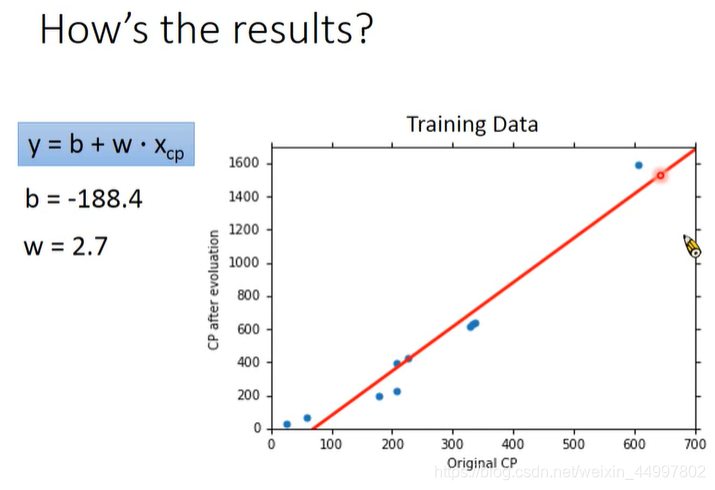
发现得到的最好的那个线性函数也不能拟合所有训练集所有实例。再抓10只,发现拟合测试集(真正关心的)的效果还可以。
如何做得更好?->引入二次模型
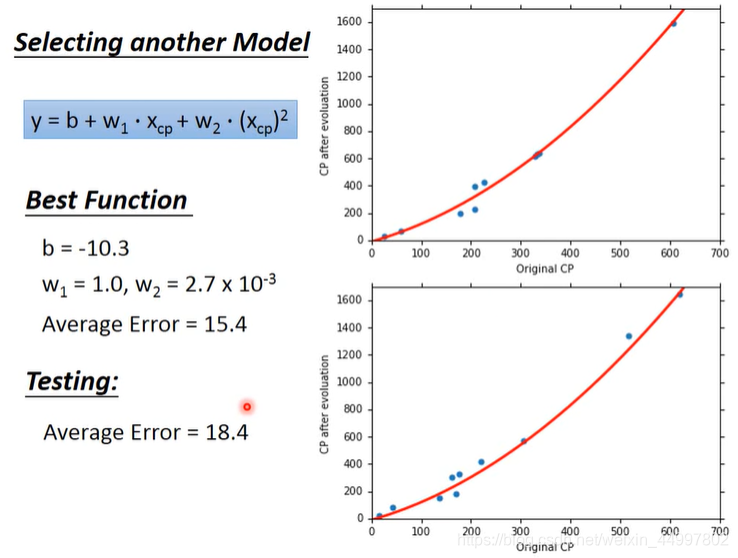
改进模型
矫枉过正
过拟合 overfitting
想拟合得更好,不断增加函数的次数直到……

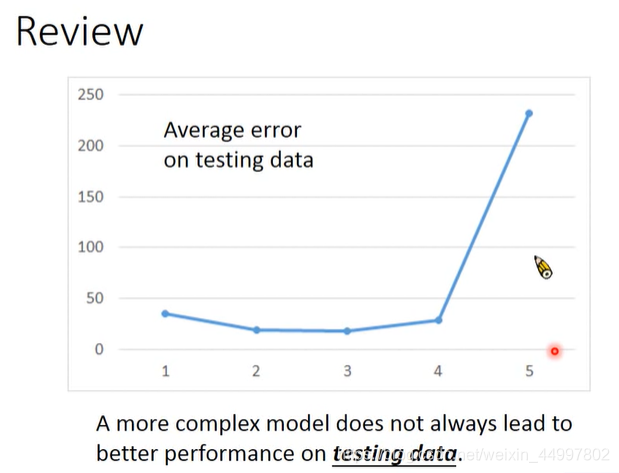
上一个Average Error是在训练集上,但是在训练集上,发现结果很离谱

比较不同次数的函数,只看训练集的图,理论上可以找到一个function,使average error越来越低,但是如果结合测试集上的average error来看呢?

结论:不是越复杂的函数,在测试集上结果越好。我们要选最合适的而不是最复杂的模型。
当收集更多的宝可梦,发现还有一个影响CP值的隐藏因素——宝可梦的物种。将不同物种用不同颜色标注。

说明最开始的Model选择就是错误的,需要改进,改进结果如下

按照刚才的方法,最终结果如何?

解决方案
初衷-把一些之前没考虑到的因素加进去,重新定义模型
增加Regularization项(正则化)
改变Loss函数,希望w更小
这样输出对输入就越不敏感,函数更光滑
输入的delta x在输出中表现为w*delta x
为什么希望不敏感?
抵抗噪声干扰的能力更强

改变Lambda的大小,Lambda越小,regularization项的影响力越小,
Lambda越大,函数越光滑,对输入越不敏感,结果如下图所示
原因是:Lambda越大,越倾向于考虑w本来的值,考虑error就越少,故训练集上的error是上升了
结论:我们倾向比较平滑的函数,因为对结果不怎么敏感,但是过于平滑,想象一条水平线,什么也干不成。反而在测试集上得到一个糟糕的结果。
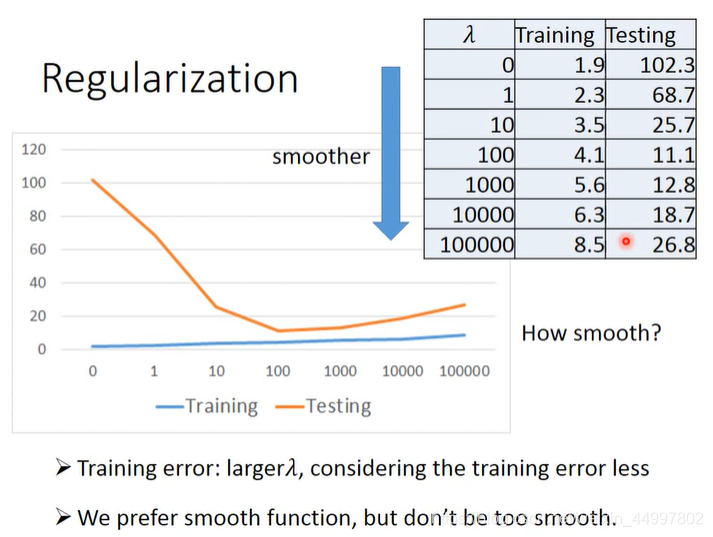
到底 how smooth 最好?
问题转化为调整Lambda。
做regularization不需要考虑偏置b。
本课结论
1)宝可梦进化后的CP值和进化前的CP值与物种有很大关系。
2)提到了梯度下降方法,之后会讲原理和技巧。theory and tips
3) overfitting 和它的一个解决方案regularization
相关文章:

PHP简单封装MysqlHelper类
MysqlHelper.class.php 1: <?php 2: 3: /** 4: * Mysql数据帮助类 5: */ 6: class MysqlHelper 7: { 8: function __construct() 9: { 10: if(isset($conn)){return;} 11: //创建连接对象 12: $this->connmysql_connect($this->…

python之XML文件解析
python对XML的解析 常见的XML编程接口有DOM和SAX,这两种接口处理XML文件的方式不同,当然使用场合也不同。 python有三种方法解析XML,分别是SAX,DOM,以及ElementTree三种方法。 以下案例依次介绍三种方法: 先…

这句话真他妈经典
研究解决一个问题的时候,通常花百分之二十的时间和精力,就能抓住问题的百分之八十,而为了完善那余下的百分之二十,却往往要花百分之八十的时间和精力 这句话真他妈经典,呵呵 转载于:https://www.cnblogs.com/webcool…
hung-yi lee_p4_Bias And Variance
文章目录本节目的biasvariance结论(鱼和熊掌不可得兼)如何解决减小bias的方案减小variance的方案对训练集进行处理得到更好的模型本节目的 where does the error come from?(为什么最复杂的模型反而Loss函数的值越大) error有…

感觉 Data Access Application Block(DAAB) 里也有可能写得不太好的地方
昨天下载了博客园的代码,里面有一个Data\SqlServer.cs我不清楚是不是 MS DAAB 里的原样文件。不过前面有声明如下:////Microsoft Data Access Application Block for .NET 3.0////SqlServer.cs////This file contains the implementations of the AdoHel…

微软压力测试工具 web application stress
WEB服务器的压力测试工具~ 115808 2009年8月1日lbimba 铜牌会员 这里给广大的煤油推荐一个web网站压力测试工具。它可以用来模拟多个用户操作网站,在程序投入运行时,可以用它来进行程序的测试并得到Web站点的稳定 参数,甚至于可以对一台小型的…

Didn't find class net.oschina.app.AppContext on
原因 你引入的Lib 未打钩 然后在 菜单Project -> Properties -> Java Build Path -> Order & Export, 然后选中你未打钩的, 然后菜单 Project->Clean,然后运行程序即可。转载于:https://blog.51cto.com/12237592/2129523

hung-yi lee_p5-7_Gradient Descent(梯度下降)
原视频地址 https://www.bilibili.com/video/BV1JE411g7XF?p5 文章目录梯度下降是如何优化函数的tips1. 使用Adagrad2. Stochastic Gradient Descent3. Feature Scaling梯度下降理论基础梯度下降的局限性梯度下降是如何优化函数的 前情回顾:损失函数是用来衡量找到…

第九章 9.2 数组的方法(Array Methods)
注:这里只讲解一些 Array() 的最重要的方法。其他更多的参考手册。9.2.1 join() 将所有元素转换为字符串并默认用 "," 连接。可以指定一个附加的参数来自定义分隔符: vara [1, 2, 3];vars a.join(); //s "1,2,3"s a.join(", &…

HashMap vs. TreeMap vs. Hashtable vs. LinkedHashMap
http://www.importnew.com/8658.html转载于:https://www.cnblogs.com/passer1991/p/3520563.html

php7+的php-fpm参数配置,注意事项
安装php7的,如果php-fpm的这几个参数设置不当了,会导致php-fpm启动不了,nginx站点不能解析php文件,报404错误。 相关命令:centos7,启动php-fpm: systemctl start php-fpm查看php-fpm是否启动&am…

hung-yi lee_p10_分类/概率生成模型
文章目录研究背景本节目的本节要使用的例子研究过程把分类当成回归来算理想做法找到最佳函数的方法研究成果运用运用过程结果方法改进模型总结讨论为什么选择正态分布模型?关于后验概率的求法之化简与改进猜想一张图总结研究背景 本节目的 Classification:Probabi…

【跃迁之路】【495天】程序员高效学习方法论探索系列(实验阶段252-2018.06.15)...
(跃迁之路)专栏 实验说明 从2017.10.6起,开启这个系列,目标只有一个:探索新的学习方法,实现跃迁式成长实验期2年(2017.10.06 - 2019.10.06)我将以自己为实验对象。我将开源我的学习方法,方法不断…

wpf+xml实现的一个随机生成早晚餐的小demo
话说每到吃完的时间就发愁,真的不知道该吃什么,然后就想到做一个生成吃什么的小软件,既然这个软件如此的简单,就打算用wpf开发吧,也不用数据库了,直接保存在xml中就可以了 程序整体结构如下图 首先我写了一…
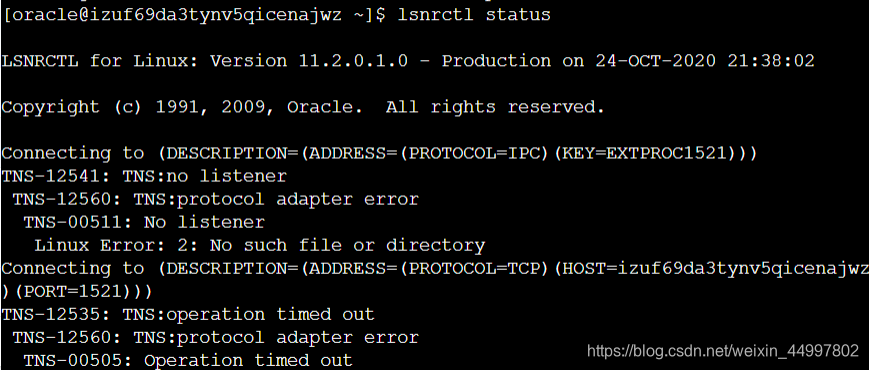
CentOS报错:TNS-12541: TNS:no listener TNS-12560: TNS:protocol adapter error TNS-00511: No listener
问题描述 原因 listener.ora中的ORACLE_HOME错了 解决 这个错误当时是和另一条指令lsnrctl start的错误一起报的,那个已解决,详细做法请各位移步我的另一篇博客 https://blog.csdn.net/weixin_44997802/article/details/109266708

c#数据结构———二叉查找树
using System;<?xml:namespace prefix o ns "urn:schemas-microsoft-com:office:office" />namespace BinaryTreeLibrary{///创建的是二叉查找树,没有重复的结点值///特点:左支树中任何值都小于父结点值,右结点任何值大于…

Spring事务管理只对出现运行期异常进行回滚
使用spring难免要用到spring的事务管理,要用事务管理又会很自然的选择声明式的事务管理,在spring的文档中说道,spring声明式事务管理默认对非检查型异常和运行时异常进行事务回滚,而对检查型异常则不进行回滚操作。那么什么是检查…

struts学习笔记三-国际化
在程序设计领域,人们把能够在无需改写有关代码的前提下,让开发出来的应用程序能够支持多种语言和数据格式的技术称为国际化技术。 国际化简称为 i18n,根据internationalization简化而来。 本地化简称为l10n,根据localization简化而…

TNS-01201: Listener cannot find executable /u01/oracle/bin/extproc for SID orcl Listener failed to
文章目录问题描述原因解决过程结果问题描述 原因 listener.ora文件中ORACLE_HOME的路径错了,导致按照这个路径找不到extproc 解决过程 首先去找ORACLE_HOME的路径 先切换为root用户(这样查找时不会有文件夹进不去) 输入指令 su root然后…

与技术无关的书单--你可以笑着说有些是“精神鸦片”
??? 转载于:https://www.cnblogs.com/crmhf/p/3823130.html

隐马尔科夫模型HMM(一)HMM模型
2019独角兽企业重金招聘Python工程师标准>>> 隐马尔科夫模型(Hidden Markov Model,以下简称HMM)是比较经典的机器学习模型了,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。当然&am…
stella forum v 2.0 的两款主题样式
stella forum v 2.0 的开发工作已经快结束啦,现在我正在加紧努力,想在本周内完成,因为下个星期我可能会不在学校。 下面公开一下我在做的两款主题,第一个是以前v1 版用的经典论坛的样式,而下面的第二款来自一个我很喜欢…

startup mount报错:invalid value given for the diagnostic_dest init.ora parameter
问题描述 解决思路 找到错误控制信息输出路径下的init文件 (我的不知道为什么叫做initORCL.ora) 将其中的ORACLE_BASE修改为正确路径 解决过程 输入指令 vi /db/app/oracle/product/11.2.0/dbs/initORCL.ora将其中三个涉及到ORACLE_BASE的地方该为正…

java的常用包
java.applet: 包含一些用于创建Java小应用程序的类。运行于html页面中。java.awt :包含一些用于编写与平台无关的图形界面(GUI)应用程序的类。java.io:包含一些用作输入输出(I/O)处理的类。java…

jQuery中的 $.ajax的一些方法
1. $(document).ajaxConplete(function(){}) 1.8版本之后,只能绑定到document元素上;1.8版本之前,可以帮到其他元素上 当$.ajax执行完成之后,执行该函数。如果有多个$.ajax请求,就会执行多次;如果有两个或多…

freebsd command
ps -aux netstat -m netstat 1 top pkg_info systat -vm systat -if dmesg netstat -an unix/linux指令集 (简体) (原作者: 农夫) http://www.darkcc.org/fmandarkcc/index.php 转载于:https://www.cnblogs.com/funpower/archive/2005/07/09/189198.html
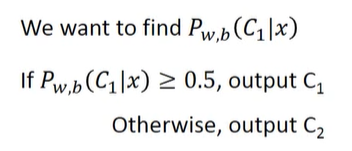
hung-yi lee_p11_逻辑回归
文章目录step1 Function Setstep2 goodness of a functionstep3 Find the best functionwhy not Logistic Regression Square ErrorDiscriminative v.s. Generative结论(判别模型的优势)解释-生成模型为何稍逊色生成模型的优势多分类模型逻辑回归的局限…

自定义状态切换按钮
最近在做一个项目,一个界面的按钮UI给画成了这样(默认状态是蓝色的然后触摸后变成灰色的) UI效果然后本着给低版本系统APP适配的职业素养(其实是不想画这种按钮),想让UI兄弟给将图标改成整个按钮效果的图片…

操作SQLite数据库
本文摘自: http://docs.blackberry.com/en/developers/deliverables/25108/Creating_and_deleting_SQLite_databases_1219776_11.jsp 创建和删除 SQLite 数据库 您可以创建临时或永久数据库。 CREATE TABLE 语句可用于创建永久(或常规)数据库…

刚开始Windows Mobile的开发,请大家多多关照
刚开始学习Windows Mobile的开发,现在正在学习WML和WAP的网站制作,请大家多多关照。转载于:https://www.cnblogs.com/czha2002/archive/2005/07/12/191129.html
