hung-yi lee_p11_逻辑回归
文章目录
- step1 Function Set
- step2 goodness of a function
- step3 Find the best function
- why not Logistic Regression + Square Error
- Discriminative v.s. Generative
- 结论(判别模型的优势)
- 解释-生成模型为何稍逊色
- 生成模型的优势
- 多分类模型
- 逻辑回归的局限性
- 死穴
- 特征转化
- 串联起逻辑回归模型
- 类神经网络
step1 Function Set
要找的是一个几率,对应不同的类别
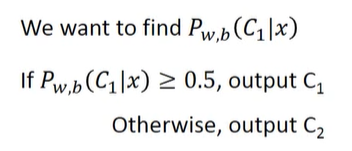
如果用高斯分布,该几率可以表示成sigma of z,其中z为


因此函数集也就是许许多多含有不同w,b的函数

图像化模型(图中z的表示错了)
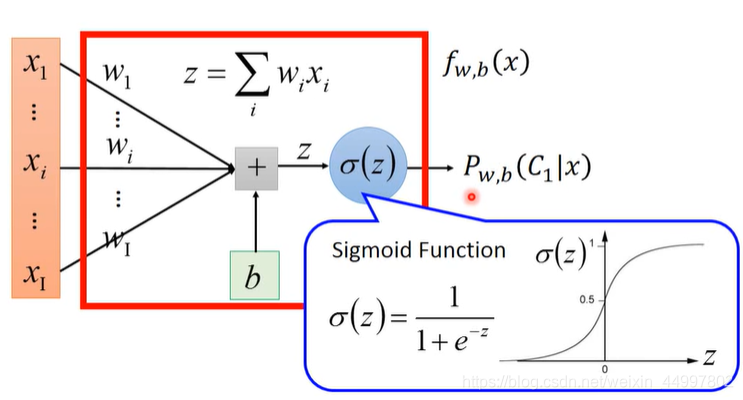
逻辑回归与线性回归对比(线性回归是最基础的嘛)

step2 goodness of a function
假设有N笔数据组成的测试数据,每笔分属于某个类别
并假设测试数据的结果是刚才的概率生成函数产生的

注:这里的概率生成函数指的是

给定w和b,就可以算出概率生成函数产生以上N笔数据组成的测试数据的几率(最大似然函数-用来衡量找到的函数的好坏)

最有可能产生以上测试数据对应的w,b也就是能使得以上函数几率最大的w,b。记作w和b(最好的w和b)

想让计算更容易,把找最大化L函数的(w,b)转化为找最小化-lnL函数的(w,b)
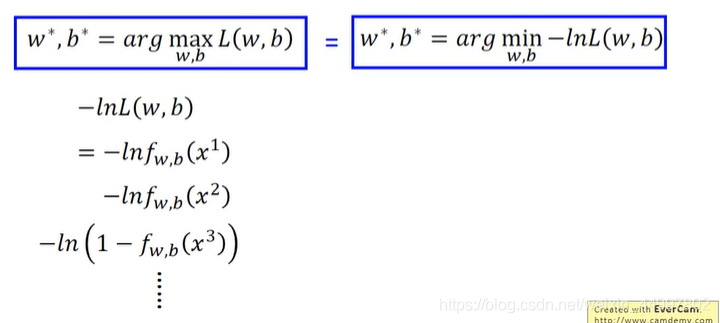
为了统一每一项的表示,写成大sigma的形式,作符号上的转换
将类别1记作1,类别2记作0(图中y^标错了,应该是110)

上式就可以写成
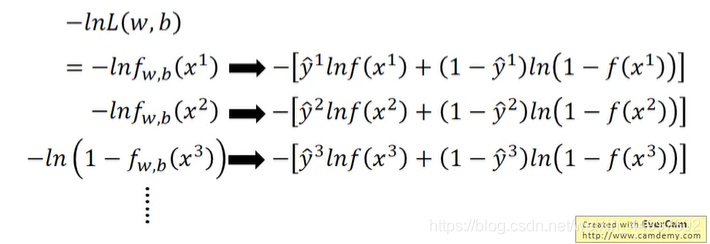
最大似然函数也就可以写成

其中中括号内的两项其实是两个伯努利分布的交叉熵(假设有两个伯努利分布p和q)
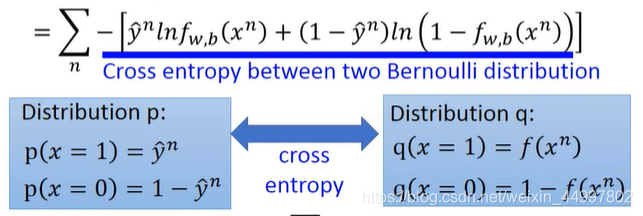
p和q的cross entropy(交叉熵)就是下式

它的作用是衡量两个分布有多接近,当两个分布一模一样,交叉熵就是0
对比逻辑回归(左)和线性回归的损失函数,结果如下
问题来了,为何不像线性回归一样直接使用平方损失/均方差作为损失函数?(见第四部分why not Logistic Regression + Square Error)

step3 Find the best function
使用梯度下降找到最佳函数
数学计算具体见视频18分钟左右
总之,对求对数、取反后的最大似然函数求导后得到的结果如下

使用梯度下降更新参数的过程如下所示

向量w更新的快慢取决于三个量①学习率(自己定)②真实结果和求出结果的差距③取决于数据的
比较逻辑回归和线性回归更新参数的方式,发现一样的
唯一不同的是f结果的取值范围

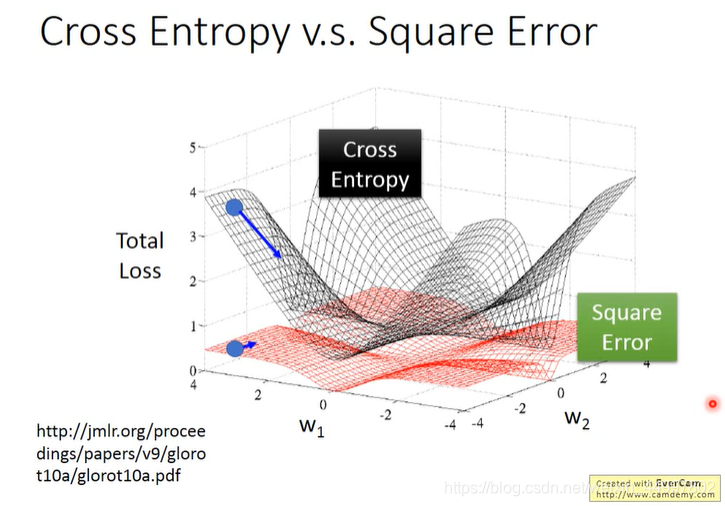
why not Logistic Regression + Square Error
如果这么做了,会造成(以类别1为例)
训练结果离真实结果很近时,微分是0(合理)
训练结果离真实结果很远时,微分是0(不合理)

这就造成,逻辑回归模型如果使用均方差作为损失函数,并使用梯度下降靠近最优解,离目标很远时,一开始就卡住了(微分为0)
Discriminative v.s. Generative
判别模型(逻辑回归)和生成模型(分类)对比
①step1 函数集相同

不同的是找w和b的过程(判别模型是直接找的,生成模型要通过概率,即要先找sigma1 sigma2 covariance)

问题是,两种方式找到的w和b一样吗?
答案是否定的。也就是两种方法是相同的函数集,找到的函数却不同。
在逻辑回归里面没有分布假设,生成模型里面假设成高斯分布、伯努利分布……
结论(判别模型的优势)
哪种方式找出的w和b更好?
来看结果
二维 难以分出胜负
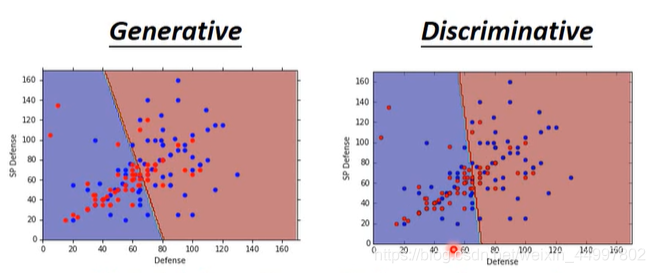
七维 判别模型的精度更高

解释-生成模型为何稍逊色
例:训练集中有13笔数据,当两个特征值都为1时,认为属于Class1,否则认为属于Class2
可以分别算出取自class1/class2的数据特征1/特征2的值为1的概率是 1 1 1/3 1/3

在测试集中,给一个已知特征1,2的值的数据,可以使用朴素贝叶斯算出其属于class1的概率
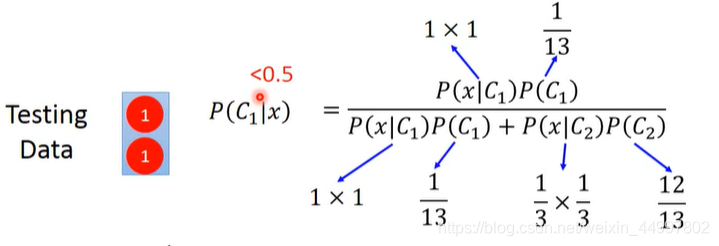
结果小于0.5,也就是认为该测试数据是属于class2。
究其根本,生成模型做了一些前提假设(脑补),它认为class2里面没出现(1,1)是因为取样取得不够多。
脑补到底好不好?通常不好,但当数据比较少时,可以很好
生成模型的优势
- 生成模型需要的数据量更小(因为有自己的假设)
- 可以忽视掉数据中的噪声(label本身有问题)
- priors and class-dependent probabilities can be estimated from different sources.
先验概率和类独立概率可以来自不同来源
ex:语音识别这两部分就能分开考虑,所以整体上用的是生成模型
多分类模型
现在有三个类别分别对应3组参数
softmax-通过指数exp的方法将最大max放大了(增大了不同输入之间的差距3 1 -3 ->20 2.7 0.05)并且将最终的结果控制在了(0,1)
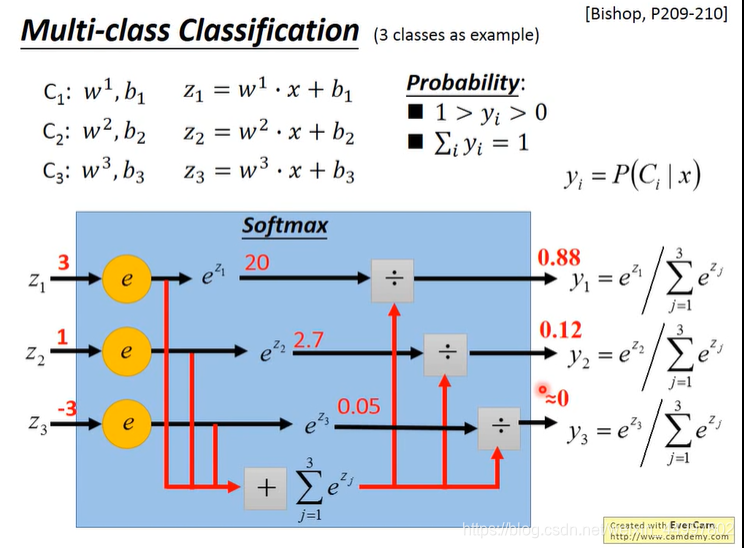
如下图,x是输入,y是由y1,y2,y3组成的输出。其中y和y^要能算交叉熵,都必须是概率分布
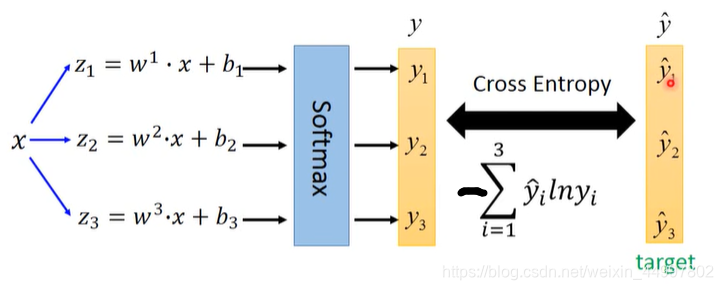
做出如下设定(好处是class1,2,3之间无谁跟谁更近)

之后就参照二分类,最小化交叉熵,找到最优函数。
逻辑回归的局限性
死穴
如果现在要做二分类,class1的两笔data分别是(0,1)(1,0),class2的两笔data分别是(0,0)(1,1)
可以画出一条直线y使得class1的两笔数据都在y>=0.5的范围而class2的两笔数据都在y<0.5的范围吗
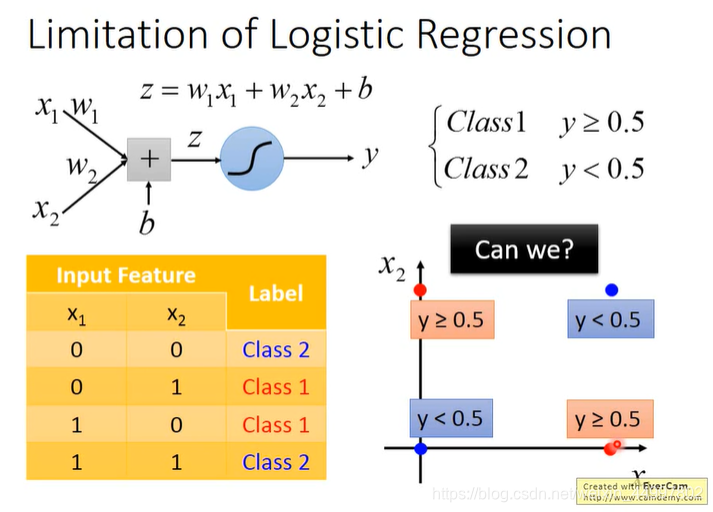
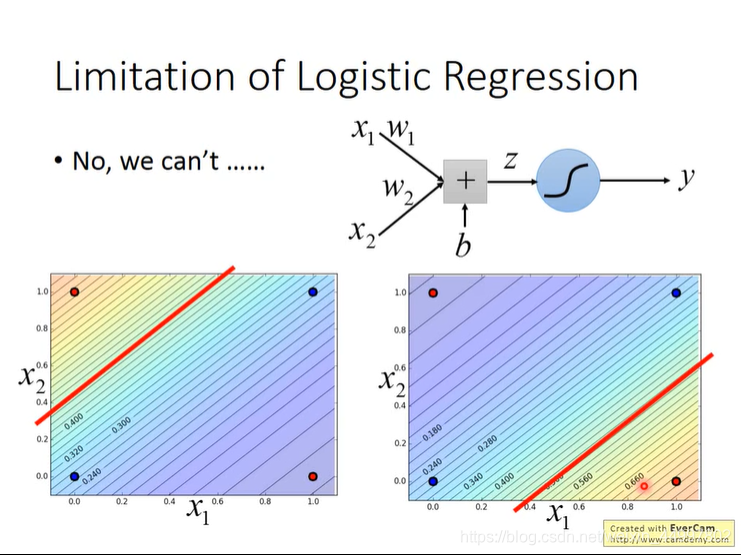
做不到!
特征转化
如果还是坚持用逻辑回归,只能做feature transformation,问题是找到好的特征转换方式并不容易,如果在上面投入太多精力,就不是机器学习了
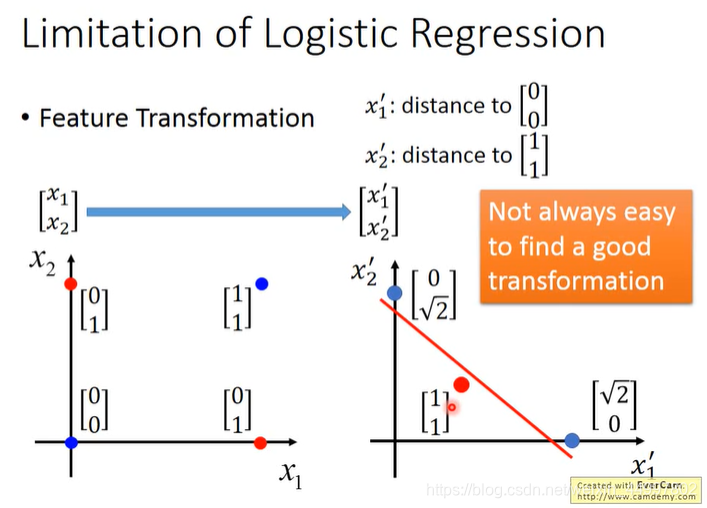
我们希望机器自己做特征转换,也就是
串联起逻辑回归模型
如下图所示,前两个逻辑回归模型做的事情是feature transformation,后一个逻辑回归模型做的事情是分类
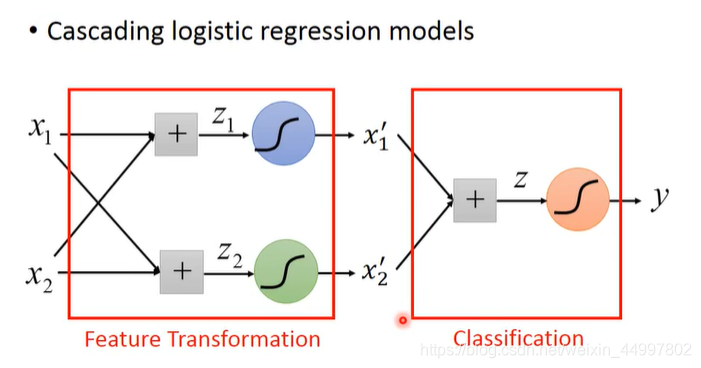
回到刚刚那个死穴,原来一个神经元没解决的难题现在被三个神经元解决了
(下图中的三幅图分别对应上图中的三个神经元模型)

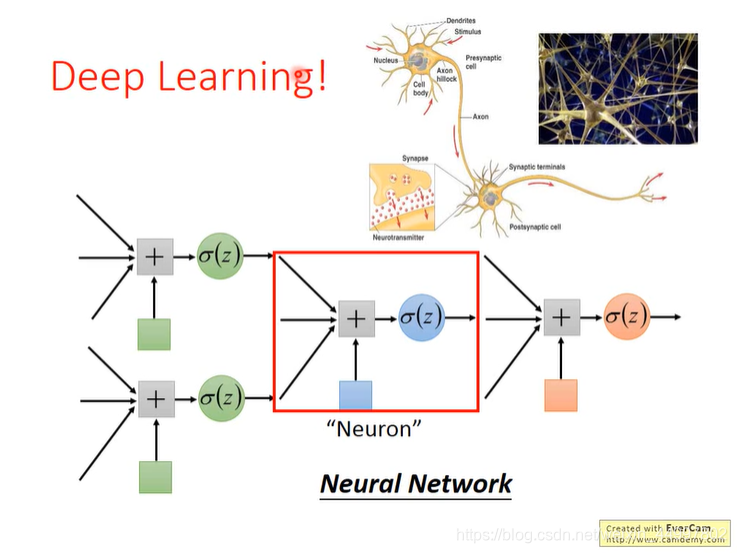
类神经网络
给多层模型换个名字,摇身一变成神经网络,也就是深度学习
相关文章:

自定义状态切换按钮
最近在做一个项目,一个界面的按钮UI给画成了这样(默认状态是蓝色的然后触摸后变成灰色的) UI效果然后本着给低版本系统APP适配的职业素养(其实是不想画这种按钮),想让UI兄弟给将图标改成整个按钮效果的图片…

操作SQLite数据库
本文摘自: http://docs.blackberry.com/en/developers/deliverables/25108/Creating_and_deleting_SQLite_databases_1219776_11.jsp 创建和删除 SQLite 数据库 您可以创建临时或永久数据库。 CREATE TABLE 语句可用于创建永久(或常规)数据库…

刚开始Windows Mobile的开发,请大家多多关照
刚开始学习Windows Mobile的开发,现在正在学习WML和WAP的网站制作,请大家多多关照。转载于:https://www.cnblogs.com/czha2002/archive/2005/07/12/191129.html
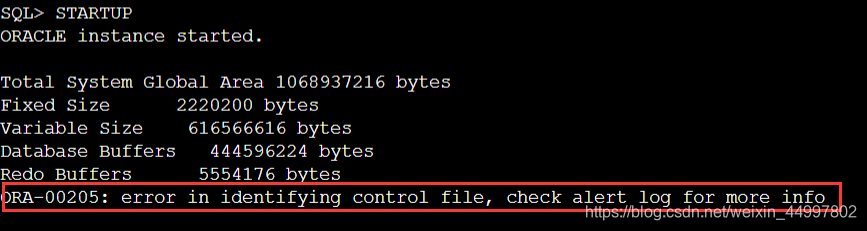
STARTUP报错:ORA-00205: error in identifying control file, check alert log for more info
问题描述 startup nomount没有异常 startup mount则出现异常,说明控制文件出错

Java基础知识回顾之六 ----- IO流
前言 在上一篇文章中,回顾了Java的多线程。而在本篇文章中主要介绍Java IO的相关知识。 IO的介绍 什么是IO? IO的名称又来是Input与Output的缩写,也就是输入流和输出流。输入流用于从源读取数据,输出流用于向目标写数据。 可以从下…

选择、分组、引用,指定匹配的位置
正则表达式的语法还包括指定选择项,对子表达式分组和引用前一子表达式的特殊字符.字符| 用于分隔供选择的字符.例如: /ab|cd|ef/ 匹配的是字符串 "ab",或者是字符串 "cd",又或者 "ef". /\d{3}|[a-z]{4}/ 匹配的是要么是一个三位数,要么是四个小写…
用Graphviz来画图 1
做了一个系统,通过配置来完成一些简单或者复杂的产品逻辑, 系统投入使用以后, 产品人员在上面配置了不少产品,产品的流程都是存放在一个xml里面,前几天突然有个想法, 打算把这个流程通过图形表示出来&#…

hung-yi lee_p12_深度学习简介
文章目录三个步骤step 1fully connect feedforward network神经网络原理从非DL到DL什么变了step 2step 3backpropagation注意这是篇头重脚轻的博客。大部分都在讲step1,2、3是飞快过去。三个步骤 step 1 许许多多的逻辑回归(神经元)模型组成…

openGL学习笔记(1)——常用方法原型解释
1、初始化,设置背景色 void glClear(int mask) 清除缓存 实參含义:GL10.GL_COLOR_BUFFER_BIT 清除颜色缓存 GL10.GL_DEPTH_BUFFER_BIT 清除深度缓存 希望同时清除多个缓存,将实參用或(|)连接即可 void …

让VBCommenter支持自定义用户名
在使用VBCommenter生成XML格式的注释时,发现在<history></history>标签内的用户名是登陆系统的用户名,而我们的用户名一般是一些简称或其它英文名等,这样在注释中想记录开发人员的真实姓名就必须手工修改,颇不方便。是…

模拟器抓取https方法
说明:为了解决安卓手线上不能抓取https请求,以下整理通过模拟器抓取https请求方法如下:前置条件:安卓模拟器1、夜神抓包工具:fiddler、charles不要安装证书 第一步安装模拟器 可以按照夜神模拟器步骤省略 第二步de.rob…

hung-yi lee_p15_机器学习深层网络比浅层网络好在哪
文章目录疑问-为什么要那么多层简单解释以语音识别为例语音识别基础GMM的方法的缺陷深度学习的高明之处回到问题-为什么一层能解决还要多层从电子工程(EE)角度解释一个电路的例子日常角度解释剪窗花Deep Learning的优点适用于参数少的情况End-to-end Learning面临复杂问题疑问-…

从WEB SERVICE 上返回大数据量的DATASET
前段时间在做一个项目的时候,遇到了要通过WEB SERVICE从服务器上返回数据量比较大的DATASET,当然,除了显示在页面上以外,有可能还要用这些数据在客户端进行其它操作。查遍了网站的文章,问了一些朋友,也找了一些解决方法. 众所周知,如果不用其它方…

ORACLE解决登陆em状态暂挂方法
1、找到oracle安装目录中db_1/计算机名_orcl/sysman/config/emd.properties , 用记事本打开emd.properties,在emd.properties文件 最后一行 的agentTZRegionGMT改为 agentTZRegionAsia/Chungking2、在dos 窗口输入 set oracle_sidorcl emctl stop dbcon…

VBA注释临时
Sub shishi() 按ABCDE为多选题定义答案; A.沙利度胺 B.异烟肼 C.利福平 d.氯法齐明 E.氨苯砜 46.各型麻风病的首选药物为(D) A.沙利度胺 B.异烟肼 C.利福平 d.氯法齐明 E.氨苯砜 45…

hung-yi lee_p13_反向传播
文章目录背景链式法则计算思路梯度计算过程/反向传播总结背景 回顾神经网络中计算梯度,更新梯度的过程 这里面的问题是,梯度是一个上百万维的向量,计算出来并非易事 这就引出了反向传播 可以说反向传播是梯度下降在神经网络中的实现。 链式…

介绍两个非常好用的Javascript内存泄漏检测工具
内存泄漏对开发者来说一般很难检测因为它们是由一些大量代码中的意外的错误引起的,但它在系统内存不足前并不影响程序的功能。这就是为什么会有人在很长时间的测试期中收集应用程序性能指标来测试性能。 最简单的检测内存泄漏的方式是用任务管理器检查内存使用情况。…

全局化和本地化
区域性En 英语en-CA 加拿大英语af-ZA 南非荷兰语eu 巴斯克语kn-IN 埃纳德语 印度tr 土耳其语Cy-uz-UZ 乌兹别克语 西里尔字母表Lt-uz-UZ 乌兹别克语 拉丁文字母表zh-CHT 繁体中文zh-CHS 简体中文设置当前区域性System.Threading.Thread.CurrentThread.CurrentCulture new Sys…

lvm讲解和磁盘故障案例
一:lvm讲解1.准备磁盘分区fdisk /deb/sdbn创建三个新分区,分别为1Gt改变分区类型为8e2.pvcreate /dev/sdb1yum install -y lvm [rootcentos7-1 ~]# yum install -y lvm 已加载插件:fastestmirror base …

hung-yi lee_p17_卷积神经网络
文章目录背景:卷积层池化层摊平KerasCNN学到了什么Deep DreamDeep Style怎么把CNN用在下围棋上为什么可以将CNN用于下围棋CNN更多应用背景: DNN拿掉一些参数就成CNN 为什么可以这样做 每一个神经元只需要图中的一部分就可以识别出想要的模式 更小的区域…
抓住青春的尾巴再愤青一把
这是今天google大神查到的:一、CAPCOM的《大神》,PS2专属ACT游戏,以三大神之一的日照处天子为原型,动作爽快华丽,是我期待很久的作品,预计今冬发售。 ... 并不是说这个水墨3D是大宇搞出来的DD,3…

the folder is already a source folder.
在新建的maven项目中,新建src/main/java时,提示the folder is already a source folder. 解决办法:右键工程,build path--configure build path--source,删除src/mian/java,再建src/main/java时即可。转载于…

selenium webdriver - 结束进程
1 import org.openqa.selenium.WebDriver;2 import org.openqa.selenium.firefox.FirefoxDriver;3 import org.openqa.selenium.os.WindowsUtils;4 /*5 * 结束进程6 */7 public class KillProcess {8 9 public static void main(String[] args) { 10 //结束进程 …

白盒测试的3中主要方法(cont.)
文章目录白盒测试简介逻辑覆盖测试法SCDCCCCDCMCCMCDC基本路径测试法BPC测试的四个步骤循环路径覆盖法白盒测试简介 静态白盒测试也称为结构化分析。 动态白盒测试又称为结构化测试。 以下所说的应该均属于动态白盒测试。 逻辑覆盖测试法 SC sentence coverage 语句覆盖 设…

CRichEdit小记
使用前要AfxInitRichEdit2(); 修改背景颜色和字体颜色 CRichEditCtrl* p(CRichEditCtrl*)GetDlgItem(IDC_RICHEDIT21);CHARFORMAT2 cf;memset((char*)&cf,0,sizeof(cf));COLORREF color;color RGB(0,255,0);cf.dwMask CFM_COLOR;cf.crTextColor color; //The text color…

学习3dmax(四)
今天没有怎么做东西,是再看一些理论的东西。这个是再网上看到的,虽然说的是如何学习3dmax,但是我个人认为学习任何一种技术都应该如此。1. 把MAX当成一门新的课程学习(和MAYA没啥关系!真的。)&…

ES6深拷贝与浅拷贝
小感在前 React学习与开发过程要经历一个相当长的准备阶段,此前看阮一峰老师的文章中,他就特别提到这一点。但是,由于React框架或者说是一种优秀的前端架构实在太诱人,所以,掌握这项技术所涉及的技术栈过程中经历的任何…
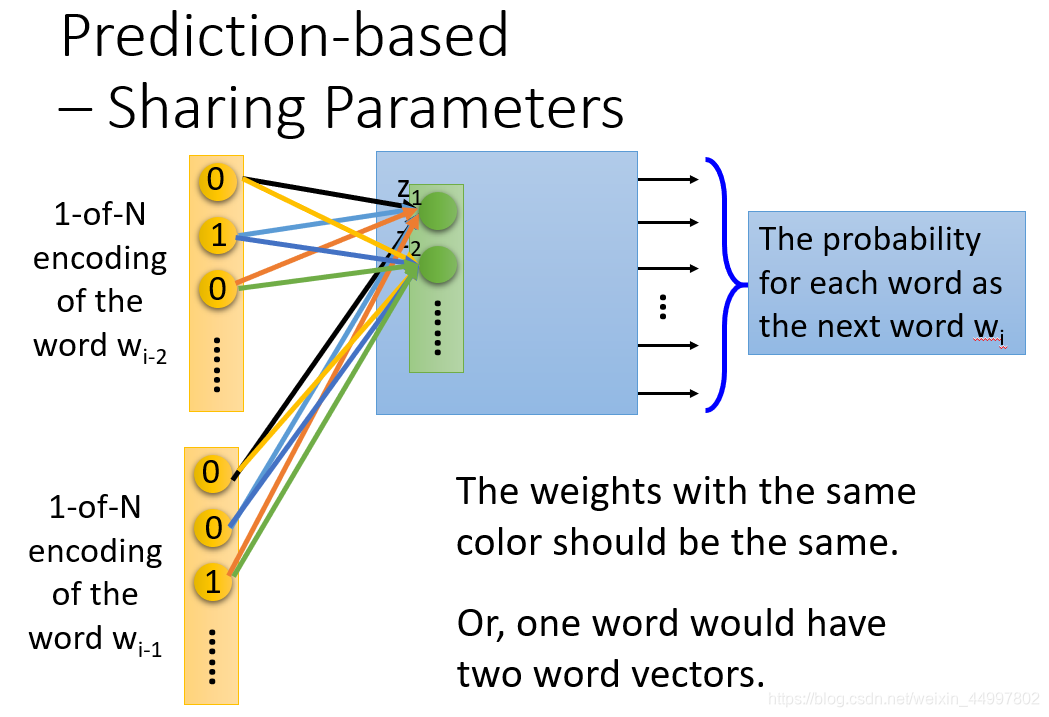
hung-yi lee_p22_无监督学习:词嵌入
文章目录原视频地址:添加链接描述输入是一个词 输出是一个向量 整个过程无监督 用来训练的是一堆文章 精神: 根据一个词汇的上下文来理解它 具体: 1.count based 两个词经常一起出现,认为它们是相似的 2.prediction-based 给神经…

用vs2010打开使用vs2013升级后的WP工程
项目在win7vs2010的环境中建立的,后来在win8.1vs2013的环境下修改和完善: 但是所有功能实现后发现wp7项目在使用vs2013打开后因为单向升级的原因,项目只能被编译为wp8项目(win8.1vs2013无法安装wp7的sdk,提示不兼容&am…

神州6号发射成功了--庆祝一下
转载于:https://www.cnblogs.com/ccBoy/archive/2005/10/12/253268.html
