hung-yi lee_p10_分类/概率生成模型
文章目录
- 研究背景
- 本节目的
- 本节要使用的例子
- 研究过程
- 把分类当成回归来算
- 理想做法
- 找到最佳函数的方法
- 研究成果运用
- 运用过程
- 结果
- 方法改进
- 模型总结
- 讨论
- 为什么选择正态分布模型?
- 关于后验概率的求法之化简与改进猜想
- 一张图总结
研究背景
本节目的
Classification:Probabilistic Generative Model(直译:分类:概率生成模型)
找到如下函数

本节要使用的例子
输入一个宝可梦,输出宝可梦的类别
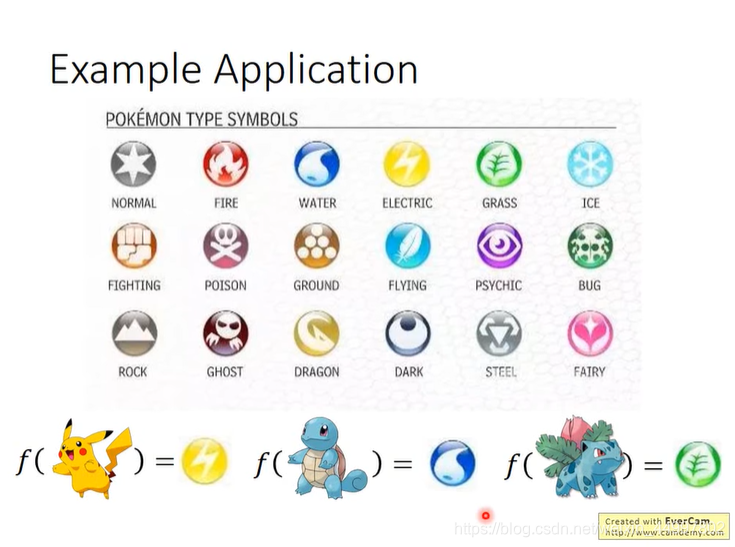
如何将输入转化为数值,我们可以提取宝可梦的如下七个属性

研究过程
把分类当成回归来算
首先以二分类为例,用1代表种类1,-1代表种类2。由于回归的输出是一个数值,我们把接近1的值当成是1,把接近-1的值当成-1。
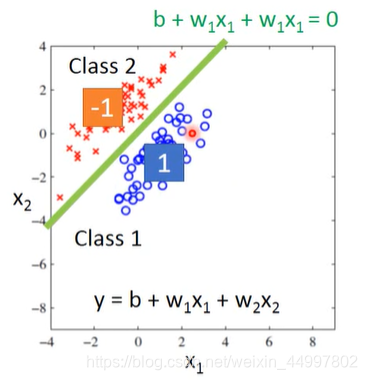
如下图所示

具体实施时,我们希望,当有如下图所示的样例分布时,红色点的(x1,x2)代入y=b+w1x1+w2x2时输出更接近-1,蓝色点更接近1,则中间那条分界线(绿线)就是b+w1x1+w2x2=0(图中标错了),在它左上方的y值是小于0的,右下方是大于0的
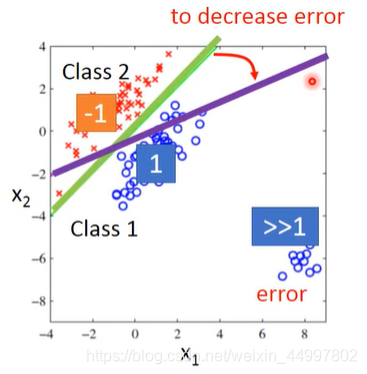
但是如果分布是如下图所示呢?在Regression看来,更好的是紫色的那条线,但在Classification看来绿色的那条线才是更适用的。显然用回归的方法来做分类此时已经不合适
这还仅仅是二分类。如果是多分类呢,如果效仿下面的做法,那么Class2与Class3的关系是要比Class1与Class3的关系更近的。但实际未必如此,所以再次印证了用回归来做分类是不合适的。

理想做法
Function(Model):希望f(x)内置一个g(x),具体如下图所示,当然这个g(x)也要能训练出来的

损失函数的定义:统计f(x)与真实结果不相等的次数,delta在预测值与真实值不相等时为1,相等时为0

找到最佳函数的方法:Perceptron SVM(但今天先不讲)
找到最佳函数的方法
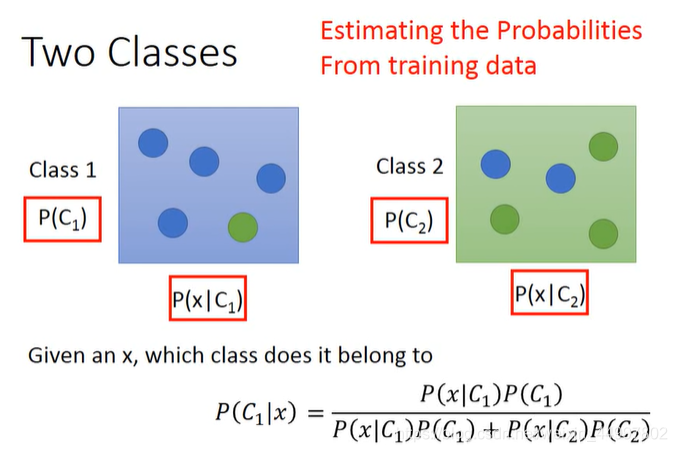
首先看下面这个例子,取出一个蓝色球,求它是从盒子1里面取出的概率

把盒子1和盒子2换成类别1和类别2,我们要计算x属于类别1的几率需要知道如下图所示4个数值。希望能从训练集把这4个数值估测出来。
这一整套想法就叫做Generative Model(生成模型)因为它能够生成某个x产生的几率。

首先来计算P(C1)和P(C2)。暂时先考虑water(水系)和normal(一般系)。并且把ID小于400的宝可梦当作是训练集,其余的当作测试集。
统计后发现ID小于400的宝可梦中有79只水系,61只一般系。则易算得P(C1)和P(C2)

接着看另外两个值的求法。从水系的神奇宝贝里面挑一只宝可梦是海龟的几率是多大?(这个海龟的ID不在前四百,即不在那79只当中)
首先明确每一只宝可梦都可以用向量来描述它的属性

把这个向量(vector)叫做特征(feature)

暂时先考虑7个当中的2个,防御力和特殊防御力。得到如下所示的图片,上面的每一个点代表一只宝可梦。
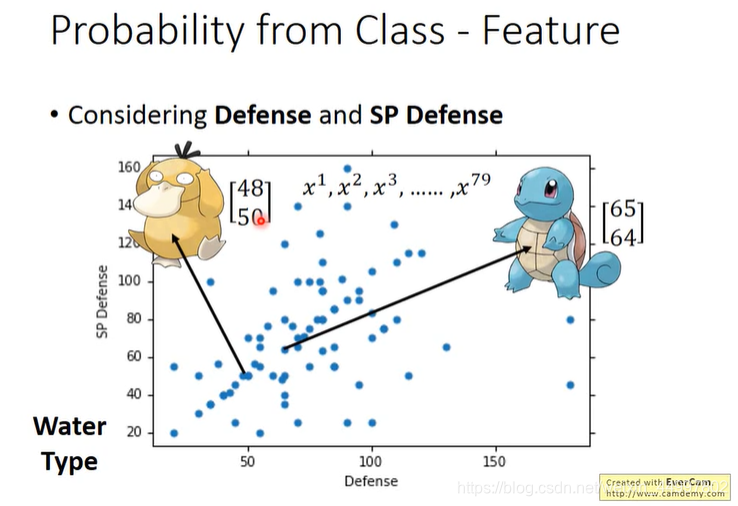
现在对于图中从未出现的点(那个海龟),怎么预测它是水系宝贝的概率?
假设选出的79个点满足Gaussian distribution(高斯分布,即正态分布)

如何理解高斯分布?
输入:向量
输出:该向量从分布当中被选出来的几率
这个函数的形状由mean mu和variance(矩阵) sigma决定的
同样mu和不同的sigma代表几率分布的最高点一样,分布不同

回到之前的问题,如何求一个新的点出现的概率。
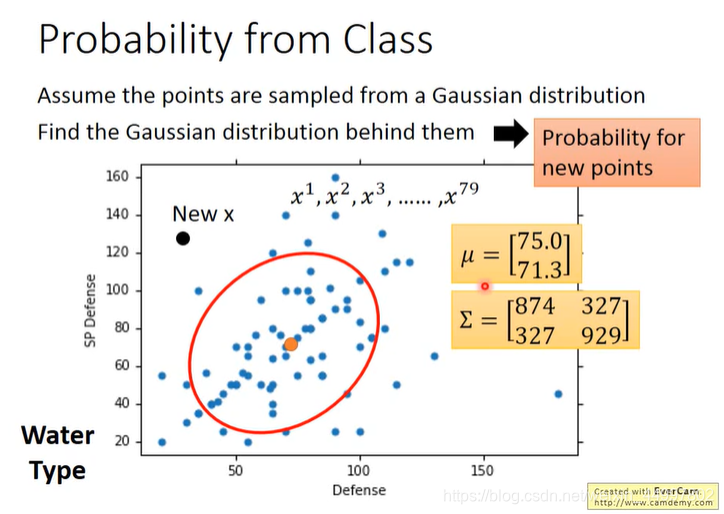
假设我们已经得到分布的mean值mu和covariance值sigma。就可以把高斯分布的f(x)写出来,这样新的点的几率就可以求得。

现在问题转化为mean值mu和covariance值sigma怎样找到?
这里用到一个方法——maximum likelihood(极大似然)
注:似然(likelihood)这个词其实和概率(probability)是差不多的意思
但是在统计里面,似然函数和概率函数却是两个不同的概念。对于这个函数:

输入有两个:x表示某一个具体的数据;θ表示模型的参数。
如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少。
如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。
最大似然法的核心是:既然一件事情已经发生了,我们就把它当作概率最大的。
具体可以参见知乎回答https://zhuanlan.zhihu.com/p/26614750
我们要用的似然函数如下(L取自likelihood)

其中

然后要做的事情是,穷举所有的mu和sigma,看哪个可以使得上面的式子的值最大,记作mu和sigma
比较直观的求法是

总结一下,最大似然法做的事是,输入一个高斯分布,输出mean值mu和covariance值sigma

研究成果运用
运用过程
现在假设我们已经得到了分类函数,即刚才想要的四个值都找到了。可以用它来求海龟是水系神奇宝贝的概率了(在式中是x属于C1的概率)。如果概率大于0.5,我们就认为这个宝贝是水系的。过程如下所示

结果
如下图所示,右上为训练集,红色区域认为是水系的宝可梦,可以看到蓝点较多,蓝色区域认为是一般系的宝可梦。将其运用到测试集上,如右下所示。准确率为47%。
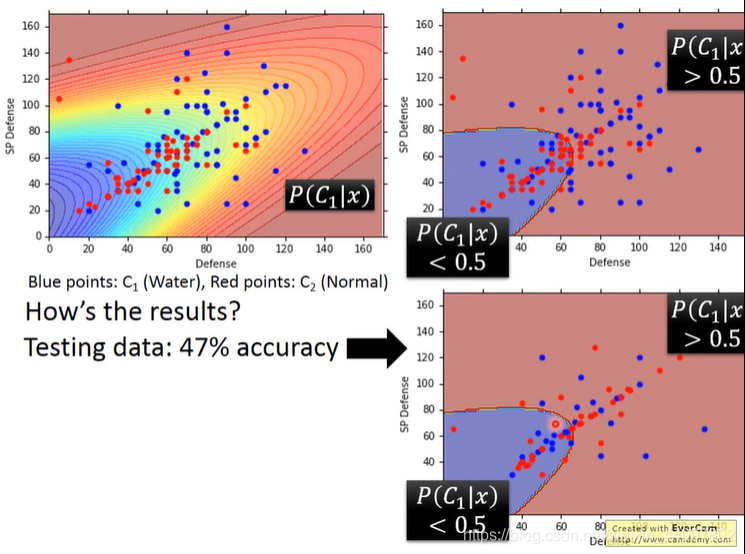
但是机器学习厉害的地方在于不止可以处理二维数据,对于七维的数据一样可以算,但发现准确率仍然只有54%。

方法改进
比较常见的情况是,不同的类型可以共享同一个covariance矩阵。
作用:减少了模型的参数。
解释:如果每个类别的分布使用不同的sigma值,会造成模型的参数多,variance也就大,也就容易过拟合。
也就是,最大似然函数会改写成如下的形式,mu1和mu2与之前的求法相同,注意共同的sigma的求法使用原先的两个sigma乘权重求和
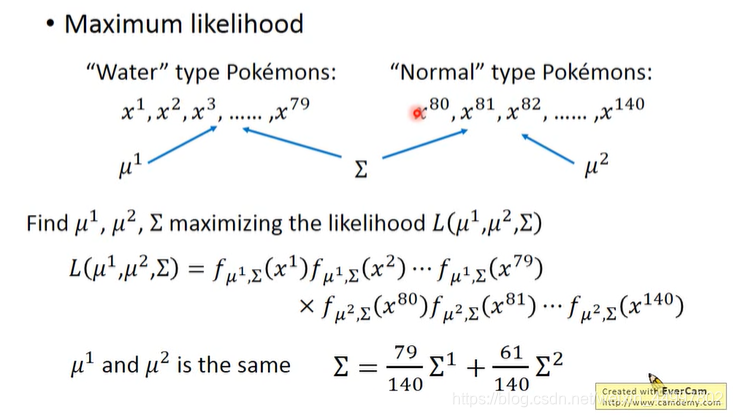
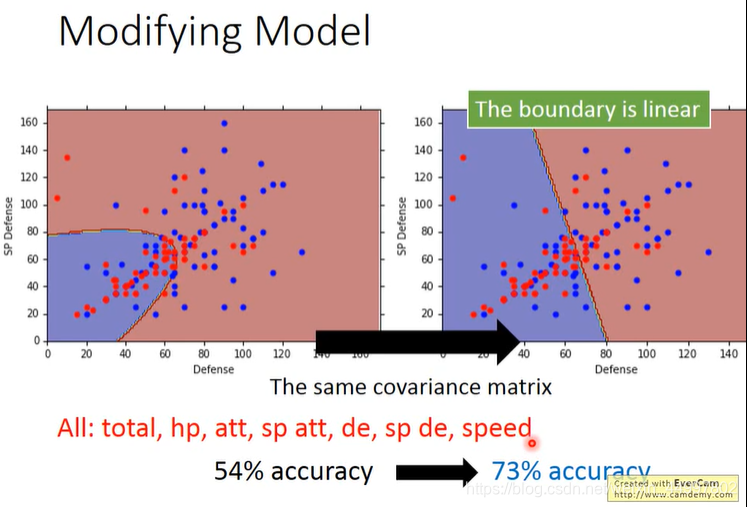
改进后的分类结果如下
发现分界线由曲转直,故也称这个模型为Linear Model
发现在七维环境下正确率上升到73%
模型总结

讨论
为什么选择正态分布模型?
概率分布的选择未必一定要是高斯分布。选择简单的模型,bias就大,variance就小;反之相反。
如果遇到两个属性组成的特征(二维)情况,可以采用伯努利分布。
如果假设所有维度都是独立的,可以采用朴素贝叶斯分类器。
关于后验概率的求法之化简与改进猜想
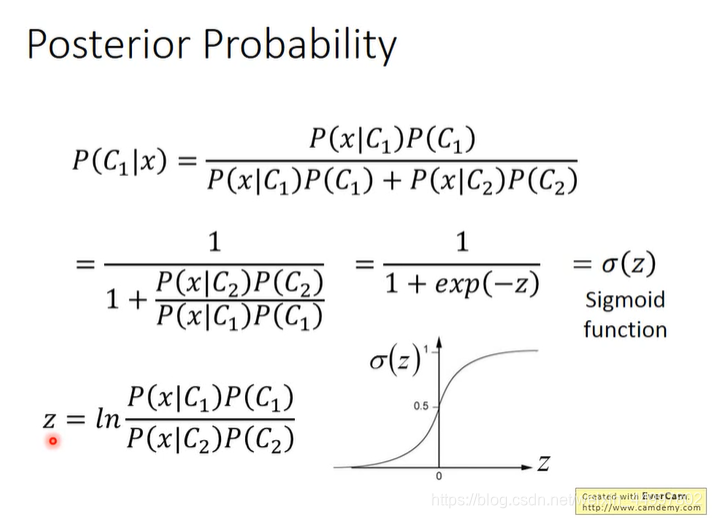
之前用来算后验概率的函数其实是z的sigmoid函数
接下来的问题是z应该如何求得

将上式化简

进一步化简和替换

但是注意到covariance的值 sigma是共用的

发现组成z的四项当中只有第一项是含有x的,我们将其记作w^T,后三项之和记作b

因而z的sigmoid函数可以简写为

也就是我们得到w和b的方法是通过N1 N2 mu1 mu2 sigma

为什么要舍近求远呢?为什么不直接求出w和b呢?这就是下一节逻辑回归要讲的内容。
一张图总结

相关文章:

【跃迁之路】【495天】程序员高效学习方法论探索系列(实验阶段252-2018.06.15)...
(跃迁之路)专栏 实验说明 从2017.10.6起,开启这个系列,目标只有一个:探索新的学习方法,实现跃迁式成长实验期2年(2017.10.06 - 2019.10.06)我将以自己为实验对象。我将开源我的学习方法,方法不断…

wpf+xml实现的一个随机生成早晚餐的小demo
话说每到吃完的时间就发愁,真的不知道该吃什么,然后就想到做一个生成吃什么的小软件,既然这个软件如此的简单,就打算用wpf开发吧,也不用数据库了,直接保存在xml中就可以了 程序整体结构如下图 首先我写了一…
CentOS报错:TNS-12541: TNS:no listener TNS-12560: TNS:protocol adapter error TNS-00511: No listener
问题描述 原因 listener.ora中的ORACLE_HOME错了 解决 这个错误当时是和另一条指令lsnrctl start的错误一起报的,那个已解决,详细做法请各位移步我的另一篇博客 https://blog.csdn.net/weixin_44997802/article/details/109266708

c#数据结构———二叉查找树
using System;<?xml:namespace prefix o ns "urn:schemas-microsoft-com:office:office" />namespace BinaryTreeLibrary{///创建的是二叉查找树,没有重复的结点值///特点:左支树中任何值都小于父结点值,右结点任何值大于…

Spring事务管理只对出现运行期异常进行回滚
使用spring难免要用到spring的事务管理,要用事务管理又会很自然的选择声明式的事务管理,在spring的文档中说道,spring声明式事务管理默认对非检查型异常和运行时异常进行事务回滚,而对检查型异常则不进行回滚操作。那么什么是检查…

struts学习笔记三-国际化
在程序设计领域,人们把能够在无需改写有关代码的前提下,让开发出来的应用程序能够支持多种语言和数据格式的技术称为国际化技术。 国际化简称为 i18n,根据internationalization简化而来。 本地化简称为l10n,根据localization简化而…

TNS-01201: Listener cannot find executable /u01/oracle/bin/extproc for SID orcl Listener failed to
文章目录问题描述原因解决过程结果问题描述 原因 listener.ora文件中ORACLE_HOME的路径错了,导致按照这个路径找不到extproc 解决过程 首先去找ORACLE_HOME的路径 先切换为root用户(这样查找时不会有文件夹进不去) 输入指令 su root然后…

与技术无关的书单--你可以笑着说有些是“精神鸦片”
??? 转载于:https://www.cnblogs.com/crmhf/p/3823130.html

隐马尔科夫模型HMM(一)HMM模型
2019独角兽企业重金招聘Python工程师标准>>> 隐马尔科夫模型(Hidden Markov Model,以下简称HMM)是比较经典的机器学习模型了,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。当然&am…
stella forum v 2.0 的两款主题样式
stella forum v 2.0 的开发工作已经快结束啦,现在我正在加紧努力,想在本周内完成,因为下个星期我可能会不在学校。 下面公开一下我在做的两款主题,第一个是以前v1 版用的经典论坛的样式,而下面的第二款来自一个我很喜欢…

startup mount报错:invalid value given for the diagnostic_dest init.ora parameter
问题描述 解决思路 找到错误控制信息输出路径下的init文件 (我的不知道为什么叫做initORCL.ora) 将其中的ORACLE_BASE修改为正确路径 解决过程 输入指令 vi /db/app/oracle/product/11.2.0/dbs/initORCL.ora将其中三个涉及到ORACLE_BASE的地方该为正…

java的常用包
java.applet: 包含一些用于创建Java小应用程序的类。运行于html页面中。java.awt :包含一些用于编写与平台无关的图形界面(GUI)应用程序的类。java.io:包含一些用作输入输出(I/O)处理的类。java…

jQuery中的 $.ajax的一些方法
1. $(document).ajaxConplete(function(){}) 1.8版本之后,只能绑定到document元素上;1.8版本之前,可以帮到其他元素上 当$.ajax执行完成之后,执行该函数。如果有多个$.ajax请求,就会执行多次;如果有两个或多…

freebsd command
ps -aux netstat -m netstat 1 top pkg_info systat -vm systat -if dmesg netstat -an unix/linux指令集 (简体) (原作者: 农夫) http://www.darkcc.org/fmandarkcc/index.php 转载于:https://www.cnblogs.com/funpower/archive/2005/07/09/189198.html
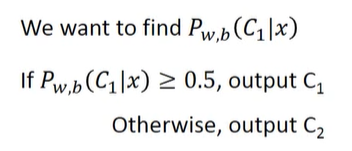
hung-yi lee_p11_逻辑回归
文章目录step1 Function Setstep2 goodness of a functionstep3 Find the best functionwhy not Logistic Regression Square ErrorDiscriminative v.s. Generative结论(判别模型的优势)解释-生成模型为何稍逊色生成模型的优势多分类模型逻辑回归的局限…

自定义状态切换按钮
最近在做一个项目,一个界面的按钮UI给画成了这样(默认状态是蓝色的然后触摸后变成灰色的) UI效果然后本着给低版本系统APP适配的职业素养(其实是不想画这种按钮),想让UI兄弟给将图标改成整个按钮效果的图片…

操作SQLite数据库
本文摘自: http://docs.blackberry.com/en/developers/deliverables/25108/Creating_and_deleting_SQLite_databases_1219776_11.jsp 创建和删除 SQLite 数据库 您可以创建临时或永久数据库。 CREATE TABLE 语句可用于创建永久(或常规)数据库…

刚开始Windows Mobile的开发,请大家多多关照
刚开始学习Windows Mobile的开发,现在正在学习WML和WAP的网站制作,请大家多多关照。转载于:https://www.cnblogs.com/czha2002/archive/2005/07/12/191129.html
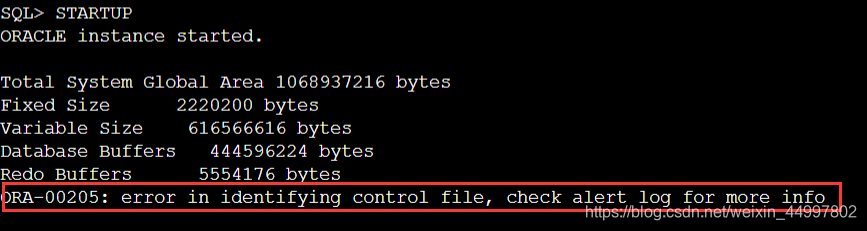
STARTUP报错:ORA-00205: error in identifying control file, check alert log for more info
问题描述 startup nomount没有异常 startup mount则出现异常,说明控制文件出错

Java基础知识回顾之六 ----- IO流
前言 在上一篇文章中,回顾了Java的多线程。而在本篇文章中主要介绍Java IO的相关知识。 IO的介绍 什么是IO? IO的名称又来是Input与Output的缩写,也就是输入流和输出流。输入流用于从源读取数据,输出流用于向目标写数据。 可以从下…

选择、分组、引用,指定匹配的位置
正则表达式的语法还包括指定选择项,对子表达式分组和引用前一子表达式的特殊字符.字符| 用于分隔供选择的字符.例如: /ab|cd|ef/ 匹配的是字符串 "ab",或者是字符串 "cd",又或者 "ef". /\d{3}|[a-z]{4}/ 匹配的是要么是一个三位数,要么是四个小写…
用Graphviz来画图 1
做了一个系统,通过配置来完成一些简单或者复杂的产品逻辑, 系统投入使用以后, 产品人员在上面配置了不少产品,产品的流程都是存放在一个xml里面,前几天突然有个想法, 打算把这个流程通过图形表示出来&#…

hung-yi lee_p12_深度学习简介
文章目录三个步骤step 1fully connect feedforward network神经网络原理从非DL到DL什么变了step 2step 3backpropagation注意这是篇头重脚轻的博客。大部分都在讲step1,2、3是飞快过去。三个步骤 step 1 许许多多的逻辑回归(神经元)模型组成…

openGL学习笔记(1)——常用方法原型解释
1、初始化,设置背景色 void glClear(int mask) 清除缓存 实參含义:GL10.GL_COLOR_BUFFER_BIT 清除颜色缓存 GL10.GL_DEPTH_BUFFER_BIT 清除深度缓存 希望同时清除多个缓存,将实參用或(|)连接即可 void …

让VBCommenter支持自定义用户名
在使用VBCommenter生成XML格式的注释时,发现在<history></history>标签内的用户名是登陆系统的用户名,而我们的用户名一般是一些简称或其它英文名等,这样在注释中想记录开发人员的真实姓名就必须手工修改,颇不方便。是…

模拟器抓取https方法
说明:为了解决安卓手线上不能抓取https请求,以下整理通过模拟器抓取https请求方法如下:前置条件:安卓模拟器1、夜神抓包工具:fiddler、charles不要安装证书 第一步安装模拟器 可以按照夜神模拟器步骤省略 第二步de.rob…

hung-yi lee_p15_机器学习深层网络比浅层网络好在哪
文章目录疑问-为什么要那么多层简单解释以语音识别为例语音识别基础GMM的方法的缺陷深度学习的高明之处回到问题-为什么一层能解决还要多层从电子工程(EE)角度解释一个电路的例子日常角度解释剪窗花Deep Learning的优点适用于参数少的情况End-to-end Learning面临复杂问题疑问-…

从WEB SERVICE 上返回大数据量的DATASET
前段时间在做一个项目的时候,遇到了要通过WEB SERVICE从服务器上返回数据量比较大的DATASET,当然,除了显示在页面上以外,有可能还要用这些数据在客户端进行其它操作。查遍了网站的文章,问了一些朋友,也找了一些解决方法. 众所周知,如果不用其它方…

ORACLE解决登陆em状态暂挂方法
1、找到oracle安装目录中db_1/计算机名_orcl/sysman/config/emd.properties , 用记事本打开emd.properties,在emd.properties文件 最后一行 的agentTZRegionGMT改为 agentTZRegionAsia/Chungking2、在dos 窗口输入 set oracle_sidorcl emctl stop dbcon…

VBA注释临时
Sub shishi() 按ABCDE为多选题定义答案; A.沙利度胺 B.异烟肼 C.利福平 d.氯法齐明 E.氨苯砜 46.各型麻风病的首选药物为(D) A.沙利度胺 B.异烟肼 C.利福平 d.氯法齐明 E.氨苯砜 45…
