Rocksdb Ribbon Filter : 结合 XOR-filter 以及 高斯消元算法 实现的 高效filter
文章目录
- 前言
- XOR-filter 实现原理
- xor filter 的构造原理
- xor filter 构造总结
- XOR-filter 和 ADD-filter对比
- XOR-filter 在计算上的优化
- Ribbon filter
- 高斯消元法
- 总结
- 参考
前言
还是起源于前几天的Rocksdb meetup,其中Peter C. Dillinger 这位大佬分享了自己为rocksdb实现的Ribbon filter。这个Filter从2020年5月份左右提的第一个PR 到现在基本已经成熟了,也已经合入到了rocksdb-master中。同时,作者因为 ribbon-filter的设计,写了一篇论文放在了arxiv上保持自己的原创性。
Ribbon filter的全称是Rapid Incremental Boolean Banding ON the fly ,能够基于真值矩阵 高效得用增量方式构建过滤器。
相比于传统的Bloom Filter 来说,它的核心差异以及 优势主要是如下几点:
- 采用XOR 方式进行按位匹配。而大多数的bloom filter都是ADD 方式进行按位匹配。
- ribbon filter的构成是 在原始key经过多个hash函数之后 由一个二维bit数组组成,并不是像传统的filter 由一个bit数组组成。
- 对CPU cache 更友好,检查一个key 是否在filter内部,ribbon filter 可以直接加载二位数组中的一个bit数组进行顺序匹配,而传统ADD filter则需要在一个bit数组上根据hash函数的结果随机匹配。
- 对空间更友好,ribbon filter存储二位数组时可以通过高斯消元法转化成上三角矩阵,更利于压缩;且加载到内存中也更利于计算。
- 消耗更多的CPU,因为ribbon filter 优化的主体是节约内存 以及 磁盘存储,而因为需要针对二维矩阵的后台计算(高斯消元),相比于传统一维数组来说会消耗更多的CPU。
本文将主要介绍Ribbon filter的设计 以及 基于行列式的高斯消元法 在ribbon filter中的应用。
XOR-filter 实现原理
介绍Ribbon-filter之前,xor-filter 是一定先要介绍的,整个ribbon filter的设计思想都是在xor-filter的基础上演化出来的。
我们传统的 ADD - filter大体形态是这样的:

一个输入的字符串或者说序列,经过多个 hash函数生成对应的hash值,ADD-filter会将这个hash值会与对应的bit 位按位与,从而将ADD-filter的 对应bit位置0,或者置1。
最后查找的时候,将输入的key经过同样多个hash函数生成的hash值 映射到ADD-filter上,与对应bit位进行按位与,如果结果位0,则key一定不存在于ADD-Filter中,如果位1,则可能存在。
而XOR-filter 的设计形态就有很大的差异了:

首先一个输入的字符串或者数据序列经过多个hash函数生成的hash值 不会映射到一个bit位,而是映射为一个固定长度的slot,这个slot中会有多个bit位,映射的过程是 这个hash值和一个slot上的多个元素按位XOR。 然后多个hash函数产生的多个hash值会映射到多个slot上。XOR-filter 会维护着一些slots,通过将这一些slots中的bits数据做一个整体的计算生成一个唯一的hash函数保存下来。
最后用户查找输入的字符串的时候 会将多个hash函数映射的slots一起进行XOR运算,假设运算的结果是R1;同时将输入的字符串 输入到上面构造时唯一的一个hash函数中,运算的结果是R2。通过判断R1==R2来确认这个key是否存在于XOR-filter中,不想等,则一定不存在。

即判断指纹函数 中 key的值 和 几个hash(key) 的 对应k-bits 值 按位异或之后的值是否相等,相等则在表示x可能在xor-filter中,否则不在。
xor filter 的构造原理
关于xor-filter 和 fingerprint的构造,大体逻辑如下,定义以下几个关键变量:
- BBB 存放最终的k-bit 的 xor filter
- nnn 是参与构造当前 xor filter的所有key/items
- ddd 是 hash 函数的个数
- mmm 是slot 的个数
1 初始的BBB 数组的大小是m=7m=7m=7,每一个item/key 经过d=3d=3d=3个 hash函数 h1,h2,h3h1,h2,h3h1,h2,h3 的映射 分布到三个BBB的slot之中。每一个item的 k-bits值的计算是通过 h1(x)⨁h2(x)⨁h3(x)h1(x) \bigoplus h2(x) \bigoplus h3(x)h1(x)⨁h2(x)⨁h3(x) 得到的,也可以看作fingerprint(x)fingerprint(x)fingerprint(x),即 item的指纹标识。

首先我们看一下 @ 会通过三个hash函数 映射到 slot7, slot6, slot4中,我们可以看到slot7是被@ 独享的,没有被其他的 item映射到,所以slot7 能够唯一标识 @,对slot7做一个逻辑标记。对于ADD filter来说,这里的slot就是一个bit位。

2 接下来我们将@ 的映射结果从BBB 的 7 个slot中剥离下来,即对应的slot 计数-- 即可,能够看到slot6 是可以唯一标识+ item,同样,我们也对slot6 做一个+ 的标记。

3 依次 处理完所有的 input items/keys,直到最后一个 ≈\approx≈,这个时候,将最后一个符号的 fingerprint(x) 的结果,也就是h1(x)⨁h2(x)⨁h3(x)h1(x) \bigoplus h2(x) \bigoplus h3(x)h1(x)⨁h2(x)⨁h3(x) 的结果放在 slot1, slot2 ,slot4 的任意一个slot中,比如slot1,其他的slot都设置为k-bits 0即可。 然后将≈\approx≈ 的fingerprint(x)=10010fingerprint(x) = 10010fingerprint(x)=10010 的结果 与slot2,slot4 的结果按位异或 得到的结果 然后放到slot1中。 slot1′sk−bits=10010⨁00000⨁00000=10010slot1's k-bits = 10010 \bigoplus 00000 \bigoplus 00000 = 10010slot1′sk−bits=10010⨁00000⨁00000=10010

4 回填其他的item,比如⭐️
和前面的操作一样,将标识⭐️ 的fingerprint(x)=11011fingerprint(x) = 11011fingerprint(x)=11011 与其映射的三个slot: slot1,slot2,slot3 进行按位异或,将结果放在能唯一标识其结果的slot3中。slot3′sk−bits=11011⨁10010⨁0000=01001slot3's k-bits = 11011\bigoplus10010\bigoplus0000=01001slot3′sk−bits=11011⨁10010⨁0000=01001

5 同理回填其他的item 即可得到最终的xorfilter BBB 的结果

可以看到slot0和slot5 还都没有被映射过,但所有的item都已经处理完了。 这个时候,我们就将所有没有被映射过的slot设置为k-bit0,最终得到的 nnn 个items 的 BBB数组,即xorfilter 如下:

当我们查找的时候需要 通过选择的 ddd个hash函数 得到一个指纹标识,fingerprint(x)=h1(x)⨁h2(x)⨁h3(x)fingerprint(x) = h1(x)\bigoplus h2(x) \bigoplus h3(x)fingerprint(x)=h1(x)⨁h2(x)⨁h3(x),拿着这个结果和B(h1(x))⨁B(h2(x))⨁B(h3(x))B(h1(x)) \bigoplus B(h2(x)) \bigoplus B(h3(x))B(h1(x))⨁B(h2(x))⨁B(h3(x)) 进行比对,相等,则说明这个item是在这个xorfilter之中的。因为从上面的图中我们看到,对于@来说 ,他的指纹函数 很明显是由 B中的三个slot 按位异或得到的。
xor filter 构造总结
xorfilter BBB 的构造过程主要是分为两步:
- 构造唯一slot和item的映射: 将所有的item 按照ddd 个hash 函数映射到 mmm 个slot中,并且通过 peel 的过程 标记哪一个slot能唯一标识当前item
- 回填其他的 item,回填的过程就是完整构造 BBB的过程,将每一个item 的finger-print 与 对应slot 的k-bits 按位异或,得到的结果放在能唯一标识它的slot中即可。
第一步的大体的算法如下:

最终返回的结果δ\deltaδ 是一个栈,每一个元素就是我们的item 和 唯一标识它的 slot的下标的映射。
第二步的算法如下,主要是构造我们的xor-filter BBB

XOR-filter 和 ADD-filter对比
总的来说XOR-filter相比于ADD-filter有如下特点:
- 性能:XOR 查找性能相对更高一些。因为xor 过滤器采用的是bits 分组,所以每一次查找时的 hash函数之间的XOR操作都是按组进行,实现起来对cache更加友好,并不像 bit过滤器 的按位ADD操作都是随机的,很有可能造成cache-miss。
- 空间消耗:实际测试过程中XOR 过滤器和 ADD过滤器在提供相同的FP时,XOR 每一个item 平均消耗1.23n * item的空间,而ADD 则需要消耗1.44n * item。
- CPU消耗:XOR消耗更多的cpu,因为构建的时候 除了基本的bits 分组之外,需要构建一个核心的fingerprint 函数。
XOR-filter 在计算上的优化
说了这么多xor-filter的实现原理,现在我们大体知道了xor-filter的构造过程,接下来我们来看看其中可以优化的部分(也就是ribbon-filter的主要目的)。
以下几个关键变量:
- BBB 存放最终的k-bit 的 xor filter
- nnn 是参与构造当前 xor filter的所有key/items
- ddd 是 hash 函数的个数
- mmm 是slot 的个数
- bbb 是每一个slot的bit位数
从宏观来看,对于每一个输入的item,我们的结果是一个数组的数组S=m∗bS=m*bS=m∗b,而输入是 B 已经存在的 m∗bm*bm∗b的系数,输出是R=d∗bR=d*bR=d∗b 每一个key会有ddd个hash 函数进行映射 。
所以,我们可以抽象成 矩阵运算(每一个slot都是bit数组)在,这样我们就得到了一个矩阵行列式:
B∗S=RB * S = R B∗S=R
当然,构造这个行列式是ribbon-filter的过程。
为什么要将原来的 ⨁\bigoplus⨁ 转化为矩阵运算呢?
主要还是效率问题,我们通过算法可以看到 对于BBB的操作 最开始需要先对所有元素进行映射,后面找到了唯一的元素在BBB的 slot标识之后 要进行解映射;更耗CPU的是回带操作,因为不论这个slot是否全是0, 都需要进行回带。
而如果我们将这么多的 bit位的⨁\bigoplus⨁ 操作都转化为矩阵运算,高效的消元一波即可得到最终每一个元素在当前slot应该存放的结果。
Ribbon filter
因为ribbon filter的主体是xor-filter 的实现,在其上构造可以高效运算的矩阵,从而利用矩阵本身的一些高效运算来解决构造xor-filter 过程中的重复操作。
所以,我们下面我们主要介绍的是 ribbon-filter 的高斯消元的主体过程,其本身的输入和输出都是和xor-filter一样,并且判断key是否存在的逻辑也一样。当然,相比于xor-filter存在的问题显而易见,因需要为高斯消元服务而消耗过多的计算-- CPU,其查找效率以及存储成本都和xor-filter大同小异(存储成本主要是受mmm slot的个数 以及 kkk 每一个slot中bit位的个数 影响 ,容错率主要受ddd hash函数影响)。
高斯消元法
在描述高斯消元法在ribbon filter中如何使用之前,我们先了解一下什么是高斯消元法。
我们在学习线性代数时 会有提到通过行列式运算 解线性方程组的过程,其实高斯消元法就是用在求解线性方程组中,当然本身是将一个行列式转换为上三角或者下三角矩阵的过程。
我们直接来看一个高斯消元法解线性方程组的过程,如下方程组
{2x+y−z=8(L1)−3x−y+2z=−11(L2)−2z+y+2z=−3(L3)\begin{cases} 2x+y-z=8 & (L1)\\ -3x-y+2z=-11&(L2)\\ -2z+y+2z=-3&(L3) \\\end{cases} ⎩⎪⎨⎪⎧2x+y−z=8−3x−y+2z=−11−2z+y+2z=−3(L1)(L2)(L3)
对于这个方程组来说,我们原本的求解过程也是消元,通过L2-L3 消除zzz,得到一个等式;再将L1*2 + L2上得到一个等式;这样我们就有一个二元一次方程组,仅有xxx和yyy两个变量;但是,假如我们不是三元一次方程组,我们10元一次方程组,那这种方式的消元消耗的代价就非常之大。
而行列式 以及 矩阵运算 也就是高斯消元法 则能够极大得简化这个过程,大体原理是上面说到的,将线性方程组每一个未知数的系数 以及 等式的结果一起构造成一个增广矩阵;将这个矩阵通过行列式的性质转换成一个下三角矩阵就可以通过回代法进行方程组求解了,具体步骤如下:
构造增广矩阵,即线性方程组的系数矩阵 一起 其结果常量 如下:
[21−18−3−12−11−212−3]\left[ \begin{array}{ccc|c} 2 & 1 & -1 & 8\\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \end{array} \right] ⎣⎡2−3−21−11−1228−11−3⎦⎤由行列式的性质:对行列式的某一行乘以一个数,加到另一行上去,整个行列式的值保持不变。
这个性质证明也是很好证明的,因为上面有一个行所有的元素是两个元素相加得到的,那我们可以将这一个行列式进行拆分。
比如对于如下矩阵:
[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann]\left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right] ⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎦⎥⎥⎥⎤
将r1∗3r1*3r1∗3加到r2r2r2之上:[a11a12⋯a1na21+3∗a11a22+3∗a12⋯a2n+3∗a1n⋮⋮⋱⋮an1an2⋯ann]⇒[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann]+[a11a12⋯a1n3∗a113∗a12⋯3∗a1n⋮⋮⋱⋮an1an2⋯ann]\left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} +3*a_{11} & a_{22} + 3*a_{12} & \cdots & a_{2n} + 3*a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right] \\ \Rightarrow \left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right] + \left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 3*a_{11} & 3*a_{12} & \cdots & 3*a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right] ⎣⎢⎢⎢⎡a11a21+3∗a11⋮an1a12a22+3∗a12⋮an2⋯⋯⋱⋯a1na2n+3∗a1n⋮ann⎦⎥⎥⎥⎤⇒⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎦⎥⎥⎥⎤+⎣⎢⎢⎢⎡a113∗a11⋮an1a123∗a12⋮an2⋯⋯⋱⋯a1n3∗a1n⋮ann⎦⎥⎥⎥⎤
可以看到拆和之后的两个矩阵中的一个和原本的矩阵是一样的,另一个矩阵则有对应行成比例(r1r1r1和r2r2r2)的矩阵,我们可以将这个行的公因数提取出来作为矩阵的系数,也就是这个矩阵会有两个一样的行,当这个矩阵按行展开之后因为存在两个一样的行,他们的正值和负值之和的绝对值是恰好想等的,所以这个矩阵的展开值就是0。
3∗[a11a12⋯a1na11a12⋯a1n⋮⋮⋱⋮an1an2⋯ann]3*\left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right] 3∗⎣⎢⎢⎢⎡a11a11⋮an1a12a12⋮an2⋯⋯⋱⋯a1na1n⋮ann⎦⎥⎥⎥⎤
当然,还可以这样更直观的理解,n∗nn*nn∗n行列式是求n维空间的体积,也就是3*3的行列式是求一个三维空间的体积,每一个行代表一个三维空间的点,而三个点则可以表示一个立体空间,那么当两个点是成比例的时候整个三维空间就只能变成二维投影了,二维空间的体积肯定是0了。 也就是按和展开后的行列式就只剩下第一个矩阵了,而这个矩阵就是原本的矩阵。
也就是这个性质是没有任何问题的,那我们拿着这个性质: 对行列式的某一行乘以一个数,加到另一行上去,整个行列式的值保持不变;就可以开始愉快的开始消元增广矩阵了:
[21−18−3−12−11−212−3]\left[ \begin{array}{ccc|c} 2 & 1 & -1 & 8\\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \end{array} \right] ⎣⎡2−3−21−11−1228−11−3⎦⎤
矩阵消元过程,目的是转化系数矩阵位下三角:
a. 执行 r1∗32+r2r1*\frac{3}{2} + r2r1∗23+r2 以及 r1+r2r1+r2r1+r2 消元得到如下矩阵
[21−1801/21/210215]\left[ \begin{array}{ccc|c} 2 & 1 & -1 & 8\\ 0 & 1/2 & 1/2 & 1 \\ 0 & 2 & 1 & 5 \end{array} \right] ⎣⎡20011/22−11/21815⎦⎤
b. 执行 −r2∗4+r3-r2 *4 + r3−r2∗4+r3,消元得到了系数矩阵的下三角矩阵
[21−1801/21/2100−11]\left[ \begin{array}{ccc|c} 2 & 1 & -1 & 8\\ 0 & 1/2 & 1/2 & 1 \\ 0 & 0 & -1 & 1 \end{array} \right] ⎣⎡20011/20−11/2−1811⎦⎤回带,整个系数矩阵已经变成了下三角矩阵,我们可以将每一行看作原本的方程组。
{2x+y−z=8(L1)12y+12z=1(L2)−z=1(L3)\begin{cases} 2x+y-z=8 & (L1)\\ \frac{1}{2}y+\frac{1}{2}z=1&(L2)\\ -z=1&(L3) \\\end{cases} ⎩⎪⎨⎪⎧2x+y−z=821y+21z=1−z=1(L1)(L2)(L3)
其中L3L3L3可以看到已经能够得到−z=1-z = 1−z=1,则z=−1z = -1z=−1;将这个结果回带到前面的两个方程中可以得到y=1,x=3y=1, x = 3y=1,x=3。
总结
filter 存在的目的是为了加速我们的单机读性能,有效减少持久化存储中的I/O次数。
因为 单机存储系统是一个融合CPU/内存/磁盘 的系统,我们想要提升上层应用的QOS,那我们就得付出对应的CPU或者内存或者磁盘某一方面的代价。
- 对于xor-filter以及ribbon-filter来说,能够节约存储成本(1.23n*item, addfilter 是 1.42n *item),同时能够拥有相比于add-filter更高效的判断性能;而且ribbon 为了加速xor-filter的效率,通过高斯消元算法会消耗更多的CPU。
- 当然性能最好的肯定是blocked-bloomfilter,它可以按照cpu的cache-lin进行构造,但是因为实际场景它会由多个filter组成,会有存储上的冗余。同样的fp下会消耗 30%额外的内存。
更多实现和测试可以参考下面的引文。
参考
- Ribbon filter: practically smaller than Bloom and Xor
- Xor filter: Faster and Smaller Than Bloom and Cuckoo Filters
- Rocksdb - master
- xor-filter implemetation
- All filter code
相关文章:

Java项目:无库版银行管理系统(java+Gui+文档)
源码获取:博客首页 "资源" 里下载! 功能介绍: 注册用户、编辑用户、删除用户、存取款、查看流水 存入业务处理: public class depositFrame extends JFrame {private JPanel contentPane;private JTextField inputFiel…

iptables-save和iptables-restore
iptables-save用来把当前的规则存入一个文件里以备iptables-restore使用。它的使用很简单,只有两个参数:iptables-save [-c] [-t table]参数-c的作用是保存包和字节计数器的值。这可以使我们在重启防火墙后不丢失对包和字节的统计。带-c参数的iptables-s…

代码之美——Doom3源代码赏析2
http://www.csdn.net/article/2013-01-17/2813778-the-beauty-of-doom3-source-code/2 摘要:Dyad作者、资深C工程师Shawn McGrathz在空闲时翻看了Doom3的源代码,发出了这样的惊叹:“这是我见过的最整洁、最优美的代码!”“Doom 3的…

什么是JavaBean
按着Sun公司的定义,JavaBean是一个可重复使用的软件组件。实际上JavaBean是一种Java类,通过封装属性和方法成为具有某种功能或者处理某个业务的对象,简称bean。由于javabean是基于java语言的,因此javabean不依赖平台,具…
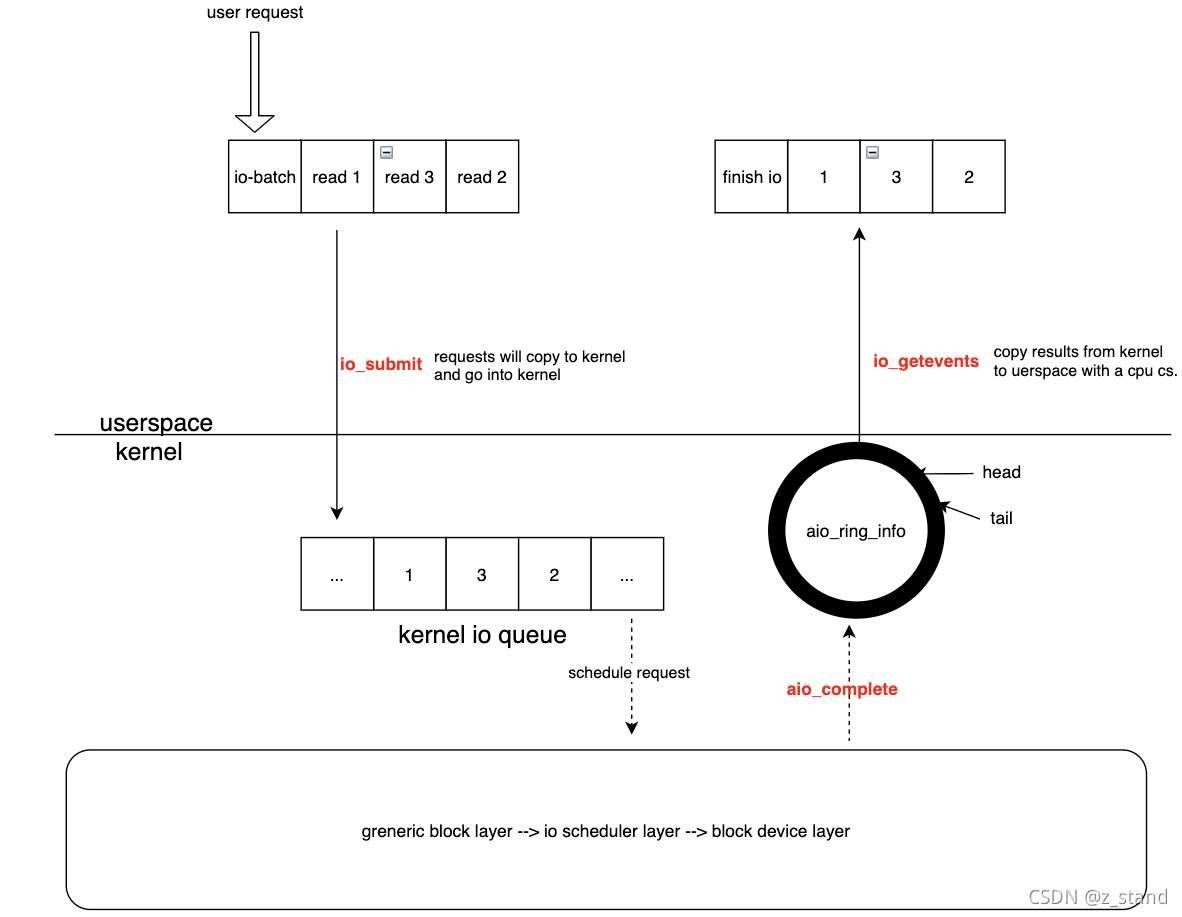
关于 linux io_uring 性能测试 及其 实现原理的一些探索
文章目录先看看性能AIO 的基本实现io_ring 使用io_uring 基本接口liburing 的使用io_uring 非poll 模式下 的实现io_uring poll模式下的实现io_uring 在 rocksdb 中的应用总结参考先看看性能 io_uring 需要内核版本在5.1 及以上才支持,liburing的编译安装 很简单&am…

添加引用方式抛出和捕获干净的WebService异常
转载:http://www.cnblogs.com/ahdung/p/3953431.html 说明:【干净】指的是客户端在捕获WebService(下称WS)抛出的异常时,得到的ex.Message就是WS方法中抛出的异常消息,不含任何“杂质”。 前提:…
Java项目:车租赁管理系统(java+Gui+文档)
源码获取:博客首页 "资源" 里下载! 功能介绍: 登陆界面、管理员界面、用户界面、汽车租赁文档 系统主页: SuppressWarnings("serial") public class SystemMainView extends JFrame implements ActionListe…
TFS中的测试计划(十)
现在有一个测试用例,用来测试登录,并且有两组测试数据。打开团队项目的web门户的测试。新建一个测试计划。命名为测试计划1添加完测试计划后,就可以向这个计划里添加测试用例了,选择登录测试。运行测试,就会生成下图左…

跟着Rocskdb 学 存储引擎:读写链路的代码极致优化
文章目录1. 读链路1.1 FileIndexer1.1.1 LevelDB sst查找实现1.1.2 Rocksdb FileIndexer实现1.2 PinnableSlice 减少内存拷贝1.3 Cache1.3.1 LRU Cache1.3.2 Clock Cache1.4 ThreadLocalPtr 线程私有存储1.4.1 version系统1.4.2 C thread_local vs ThreadLocalPtr1.4.3 ThreadL…

Java项目:人力管理系统(java+Gui+文档)
源码获取:博客首页 "资源" 里下载! 功能介绍: 角色员工、管理员,员工信息表,查询、更新,修改,移除、添加 用户管理控制层: /*** author yy*/Controller RequestMapping(…

senfile函数实例的运行过程截图
//要传输的文件内容如下所示: 启动服务器,等待客户端连接(在同一台主机上模拟的) 客户端远程登录,这里是在本地登录 这个要注意一点就是远程登陆的时候一定要带上端口号不然连接失败!!转载于:ht…

马年计划2014-2-21
新的一年到来了! 刚刚过去的一年里,我已浪费很多时光! 新年新气象,为避免重蹈覆辙,此时我必须要立个新年计划,马年计划! (1)一天必须做两道ACM题。 (2&#…

java jsp页面如何添加C标签
在https://mvnrepository.com/找两个jar包分别是: <dependency> <groupId>javax.servlet.jsp.jstl</groupId> <artifactId>jstl-api</artifactId> <version>1.2</version> </dependency> <dependency> <g…

如何用 ndctl/ipmctl 管理工具 配置不同访问模式的pmem设备
文章目录1 PMEM 底层架构2 PMEM 逻辑架构3 ipmctl 创建 不同模式的 region3.1 安装3.2 创建AppDirect mode的region3.3 创建 Memory Mode模式3.4 创建 混合模式3.5 查看创建的结果4 ndctl 创建不同类型的 namespaces4.1 安装4.2 创建/删除 一个任意类型的namespace4.3 指定类型…

[PHP]php基础练习题学习随笔
1、解释一下PHP中常量、变量、可变变量并举例说明;超级全局变量有哪些? 常量是单个值的标识符(名称),通过define()设置,在脚本中无法改变该值,常量自动全局。<?php #对大小写不敏感为true&a…

Java项目:进销存系统(java+Gui)
源码获取:博客首页 "资源" 里下载! 功能介绍: 基本信息管理、库存管理、销售管理、订单管理、日志管理、供应商基本信息、员工基本信息、商品信息、入库管理、出库管理、剩余库存 商品信息控制层: /*** <p>* 前…

IDP申请直到软件上架流程 - iOS
第一:IDP的申请 1.先在iPhone DevCenter上注册成为iphone developer 2.加入iPhone开发程序项目iPhone Developer Program Apply Now 3.打算收费的都建议选择99刀那个,QTY是个数的意思。1就好。 4.选择地区china,(很早之前没有china࿰…

灭霸—个人冲刺(4)
灵魂三问:昨天做了什么?1.手机验证码 2h 2.整体框架搭建尝试 2h 目标任务量:100% 完成任务量:100% 今天要做什么?1.数据库建立及连接 16h 遇到困难没有?2.整体框架搭建时因为连接服务器分为三类…

关于 Rocksdb 的 EnvWrapper 作用的小讨论
临下班前一位做引擎的小伙伴提了个小问题, Rocksdb 实现了非常多的Env backend 这一些backend 可以让用户根据自己需求创建不同 公共接口backend,来实现自己的文件操作或者公共线程池操作。 Env* env new rocksdb::HdfsEnv(FLAGS_hdfs) 问题是…

corepython第九章:文件和输入输出
学习笔记: OS模块代码示例: 1 import os2 for tmpdir in (/tmp,rc:\users\administrator\desktop):3 #如果存在括号里面的目录,则break4 if os.path.isdir(tmpdir):5 break6 #如果不存在,则tmpdir为空值,即False7 else:8 pri…
Java项目:学生管理系统(无库版)(java+打印控制台)
源码获取:博客首页 "资源" 里下载! 功能介绍: 学生成绩管理系统成绩表 用户管理操作: /*** 用户管理操作*/ Controller RequestMapping("/user") public class UserController {Autowiredprivate UserServi…

构建ASP.NET MVC4+EF5+EasyUI+Unity2.x注入的后台管理系统(12)-系统日志和异常的处理②...
原文:构建ASP.NET MVC4EF5EasyUIUnity2.x注入的后台管理系统(12)-系统日志和异常的处理② 上一讲我们做了日志与异常的结果显示列表,这一节我们讲要把他应用系统中来。 首先我们在App.Common类库中创建一个通用类ResultHelper,这个…

爬取猫眼怦然心动电影评论
作业要求来源:https://edu.cnblogs.com/campus/gzcc/GZCC-16SE1/homework/3159 可以用pandas读出之前保存的数据: newsdf pd.read_csv(rF:\duym\gzccnews.csv) 一.把爬取的内容保存到数据库sqlite3 import sqlite3with sqlite3.connect(gzccnewsdb.sqli…
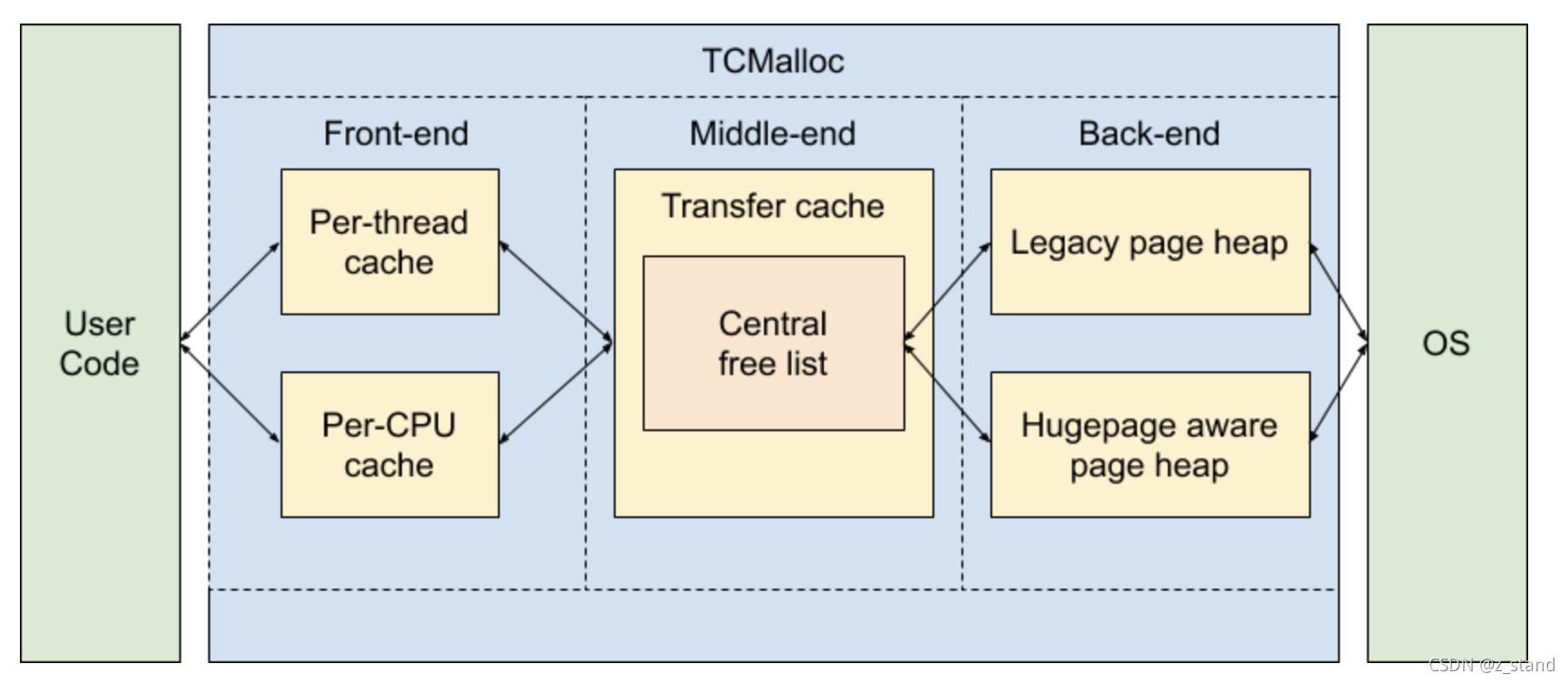
TCMalloc(Thread-Caching malloc) 基本设计原理
文章目录背景如何使用架构概览1. TCMalloc Front-end1.1 小对象和大对象的内存分配过程1.2 内存释放过程1.3 Per-CPU mode1.4 Per-thread mode1.5 per-cpu 和 per-thread 运行时内存管理算法对比2. TCMalloc Middle-end2.1 Transfer Cache2.2 Central Free List2.3 Pagemap 和 …
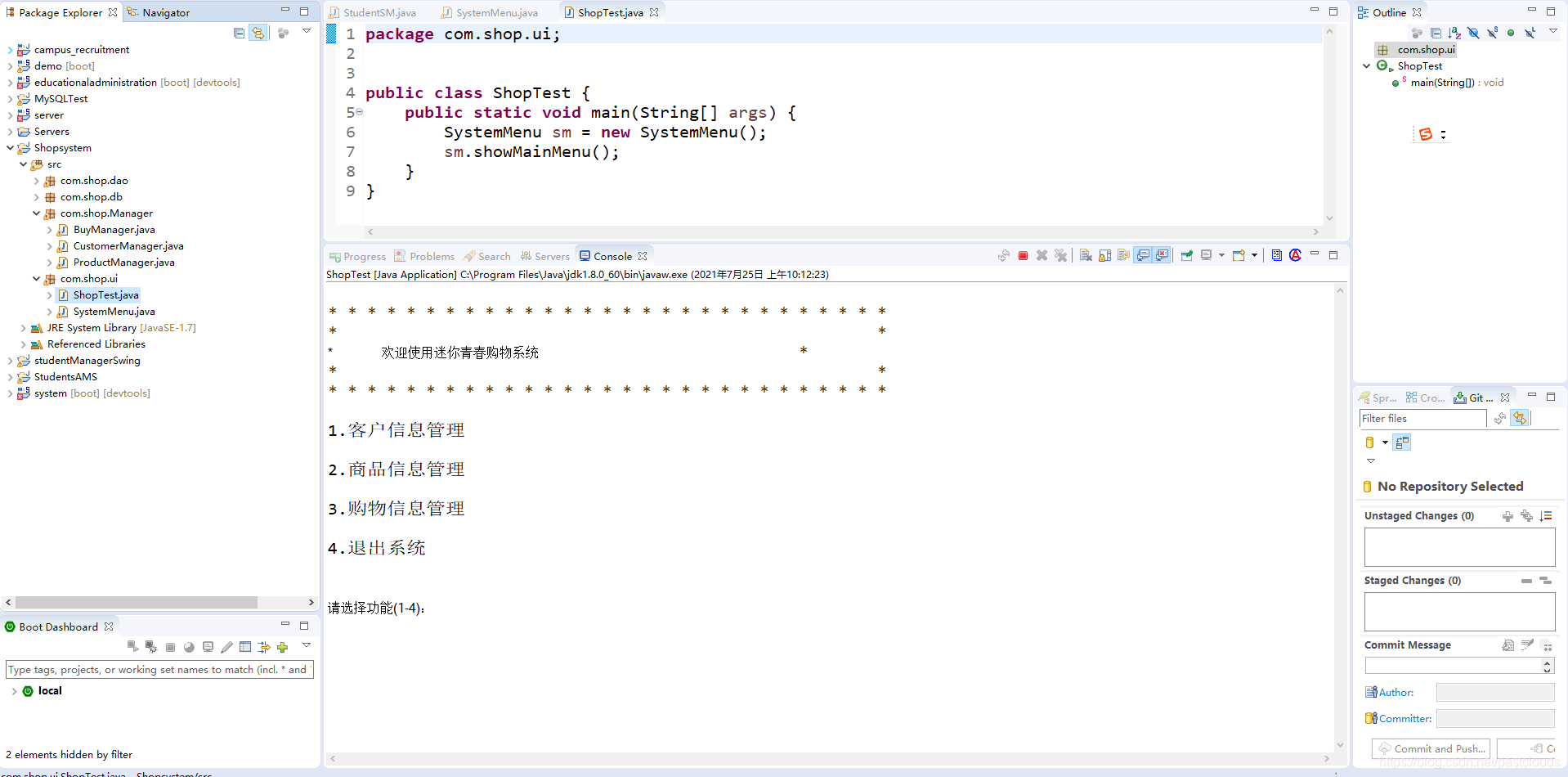
Java项目:控制台商城系统(java+打印控制台)
源码获取:博客首页 "资源" 里下载! 功能简介: 客户信息管理、商品信息管理、购物信息管理、退出系统 显示系统主菜单: public class SystemMenu {//显示系统主菜单public void showMainMenu(){System.out.println(&qu…

PAT (Basic Level) Practise (中文)-1025. 反转链表 (25)
PAT (Basic Level) Practise (中文)-1025. 反转链表 (25) http://www.patest.cn/contests/pat-b-practise/1025 给定一个常数K以及一个单链表L,请编写程序将L中每K个结点反转。例如:给定L为1→2→3→4→5→6,K为3&am…

初识Quartz(三)
为什么80%的码农都做不了架构师?>>> 简单作业: package quartz_project.example3;import java.util.Date;import org.quartz.Job; import org.quartz.JobExecutionContext; import org.quartz.JobExecutionException; import org.quartz.Job…

内存分配器设计的演进
文章目录栈内存空间是否够用系统调用申请内存最简单的内存分配器实现 -- bump allocator可扩容的 Bump alloactor通过free-list 管理的 allocator通过size-buckets 维护多个free-list 的 allocatorCache friendly allocator需要考虑更多问题的allocator性能易用性本文希望描述一…
Android OpenGL ES(十一)绘制一个20面体 .
前面介绍了OpenGL ES所有能够绘制的基本图形,点,线段和三角形。其它所有复杂的2D或3D图形都是由这些基本图形构成。 本例介绍如何使用三角形构造一个正20面体。一个正20面体,有12个顶点,20个面,30条边构成:…

Java项目:学生选课系统(java+javaweb+jdbc)
源码获取:博客首页 "资源" 里下载! 功能介绍: 用户菜单、学生管理、教师管理、课程管理、成绩排名查询 学生管理控制层: Controller RequestMapping("/student") public class StudentController {private …
