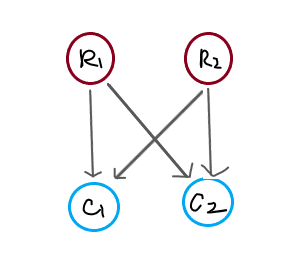
简介:同皇帝的烦恼
分析:
如果n是偶数,那么答案就是相邻两个人的r值之和的最大值
即ans=max{r(i)+r(i+1)} (i=1,2,3,…,n),规定r(n+1)=r1
这时的ans实际上是答案的下限
一个合法的方案就是,对于编号为i的人来说,如果i是奇数,那么就从1往后依次取礼物,
如果i是偶数,那么就从ans往前依次取礼物如果n是奇数,这个时候就需要二分一个ans了
L=max{r(i)+r(i+1)}
R=max{3*r(i)} =>(最坏情况下相邻的三个人全都需要不一样的礼物)
假设我们已经有了p个礼物,我们要怎么分配呢:
假设第一个人取走了1~r1的礼物,
那么编号为偶数的人就尽量往前取,编号为奇数的人就尽量往后取,同时保证相邻的人不冲突
这样就可以使1号和n号的冲突尽可能小
比如,n=5,A={2,2,5,2,5},p=8
1:{1,2}
2:{3,4}
3:{8,7,6,5,2} (3,4已经被2取走了)
4:{1,3}
5:{8,7,6,5,4}
1号和5号不冲突,所以p=8为可行解
在代码实现上,我们只要记录一下每个人在[1~r1]内拿了多少,在[r+1~p]内拿了多少
最后我们只要判断一下最后一个人有没有在[1~r1]内拿东西就好了
//这里写代码片
#include<cstdio>
#include<iostream>
#include<cstring>using namespace std;const int N=100010;
int n,r[N],lef[N],righ[N];//判断0个礼物是否足够
//left[i]是第i个人拿到的左边的礼物的总数,right同理
int pd(int p)
{int x=r[1],y=p-r[1]; //左边的个数,右边的个数 lef[1]=r[1]; righ[1]=0;for (int i=2;i<=n;i++){if (i&1){righ[i]=min(r[i],y-righ[i-1]); //尽量拿左边的礼物 lef[i]=r[i]-righ[i];}else{lef[i]=min(r[i],x-lef[i-1]); //尽量拿右边的礼物righ[i]=r[i]-lef[i]; }}return lef[n]==0;
} int main()
{while (scanf("%d",&n)!=EOF&&n){for (int i=1;i<=n;i++) scanf("%d",&r[i]);if (n==1) //1的情况要特判 {printf("%d",r[1]);continue;}int L=r[1]+r[n];int R=0;for (int i=1;i<n;i++) L=max(L,r[i]+r[i+1]);if (n&1){for (int i=1;i<=n;i++) R=max(R,r[i]*3);while (L<R){int mid=L+(R-L)/2;if (pd(mid))R=mid;else L=mid+1;} }printf("%d\n",L);}return 0;
}