传送门
Description
给出一张带边权的有向图,每个边都上都有一个字符串(给出对应Trie树上的节点),一条路径的长度为路径上的边权之和+相邻两条边的字符串的lcp长度之和。
求从1到其它节点的最短路
Solution
预备部分
首先,两个字符串的lcp,就是对应节点在Trie树上的lca的深度值。
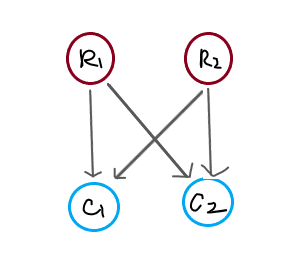
把每条边拆成两对入点和出点,分别是\(r1,r2,c1,c2\),它们之间的边权值都是原来的边权:
大概像这样?[图1]
建一个源点S,向所有原先入点是1的点连边权为0的边
然后枚举原图中的每个点\(x\),把所有形如\(<i,x>,<x,j>\)的边都连接在一起,使得边权就是两两字符串的\(lcp\)大小
求出原图对于源点的最短路
最后,对于一个点\(x\),枚举所有\(<i,x>\)的边,取它们中出点最小的\(dis\)
可是一个点的入边和出边会有很多,所以连出的边数大概是是\(O(n^2)\)的,显然不行
所以我们考虑优化建图:
接下来介绍前后缀优化建图
首先,之前把一条边拆成两对出点和入点,其中一对用来处理后缀,一对用来处理前缀
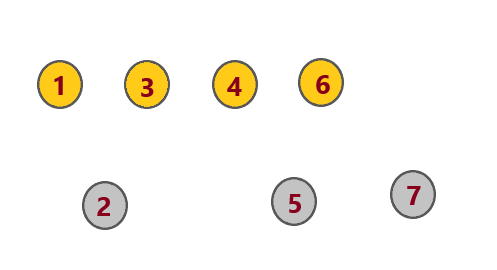
对于一个点,我们以前缀为例子:
按照每条边对应字符串在Trie树上的\(dfs\)序排序,上面是入边(\(c1\)点),下面是出边(\(r1\)点):
[图2]
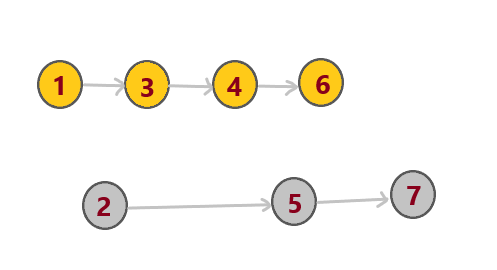
上下分别按照顺序连边权为\(0\)的有向边
[图3]
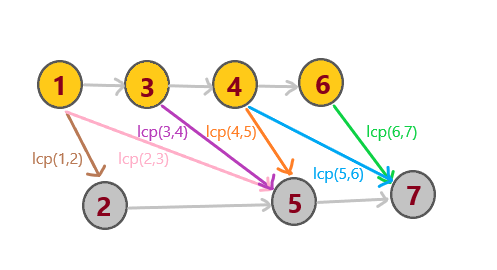
考虑到一个性质\(lcp(a_1,a_n)=\min_{i=1}^{n-1} lcp(a_i,a_i+1)\)
考虑dfs序相邻的两点\(x_i,x_{i+1}\)(有可能都是入点或出点),计算出\(lcp(x_i,x_{i+1})\),考虑它们的影响范围,显然,我们找到序号最大且小于等于\(i\)的入边\(c1_k\)和序号大于等于\(i+1\)的出边\(r1_j\),连边\(<c1_k,r1_j>\),长度为\(lcp(x_i,x_{i+1})\)
[图4]
这样,就可以满足一个序号小的入边到任意一个序号比它大的出边之间的最短路就是它们的\(lcp\)值
这是前缀优化,当然后缀优化部分与之类似,这里就不再赘述
最后,分享一下最短路的写法,貌似也不会快多少吧。。。
const ll nN=262144,inf=20000000000;
ll d[MM<<2];
struct node{ll x;int f;}t[nN<<1];
inline node Min(const node&o,const node&oo){return o.x<oo.x?o:oo;}
inline void rw(int k,ll x){for(t[k+=nN].x=x;k>>=1;)t[k]=Min(t[k<<1],t[k<<1|1]);}
inline void dij()
{reg int i,x;++tt;for(i=cc[1].size()-1;~i;--i)Ins(tt,cc[1][i]*4-3,0),Ins(tt,cc[1][i]*4-1,0);for(i=1;i<nN<<1;++i) t[i].x=inf;for(i=1;i<=tt;++i) d[t[i+nN].f=i]=inf;for(rw(tt,d[tt]=0);t[1].x!=inf;){rw(x=t[1].f,inf);for(i=hr[x];i;i=e[i].nex)if(d[e[i].to]>d[x]+e[i].w)rw(e[i].to,d[e[i].to]=d[x]+e[i].w);}
}Code
#include<bits/stdc++.h>
#define ll long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}return x*f;
}
#define reg register
#define ME(x) memset(x,0,sizeof x)
const int MK=20005,MN=50005,MM=50005;
int N,M,K,dfn[MK];
class Tire
{private: int fa[MK],dep[MK],top[MK],mx[MK],siz[MK],dind;struct ed{int to,nex;}e[MK];int hr[MK],en,vis[MK];inline void Ins(int x,int y){e[++en]=(ed){y,hr[x]};hr[x]=en;}void dfs1(int x,int d){dep[x]=d;siz[x]=1;for(reg int i=hr[x];i;i=e[i].nex)dfs1(e[i].to,d+1),siz[x]+=siz[e[i].to],(siz[e[i].to]>siz[mx[x]])?mx[x]=e[i].to:0;}void dfs2(int x,int tp){top[x]=tp;if(mx[x])dfs2(mx[x],tp);dfn[x]=++dind;for(reg int i=hr[x];i;i=e[i].nex)if(e[i].to^mx[x])dfs2(e[i].to,e[i].to);}public:inline void init(){ME(vis);ME(hr);ME(fa);ME(dep);ME(top);ME(mx);ME(siz);en=dind=0;}inline void ins(int x,int y,int w){Ins(x,y);fa[y]=x;}inline void build(){dfs1(1,0);dfs2(1,1);}inline int lca(int x,int y){for(;top[x]^top[y];)dep[top[x]]<dep[top[y]]?y=fa[top[y]]:x=fa[top[x]];return min(dep[x],dep[y]);}
}trie;
int tt;
struct edge{int to,w,nex;}e[MM*20];int en,hr[MM<<2];
int pos[MM],idt;
bool cmp(const int&o,const int&oo){return dfn[pos[std::abs(o)]]<dfn[pos[std::abs(oo)]];}
std::vector<int> rr[MN],cc[MN];
int tmp[MM],nn;
inline void Ins(int x,int y,int c){e[++en]=(edge){y,c,hr[x]};hr[x]=en;}
inline void ins(int x,int y,int c,int w)
{pos[++idt]=w;Ins(tt+1,tt+2,c);Ins(tt+1,tt+4,c);Ins(tt+3,tt+2,c);Ins(tt+3,tt+4,c);rr[y].push_back(idt);cc[x].push_back(idt);tt+=4;
}
inline void Build(int x)
{if(!rr[x].size()||!cc[x].size()) return;std::sort(rr[x].begin(),rr[x].end(),cmp);std::sort(cc[x].begin(),cc[x].end(),cmp);reg int t,i,j,len;nn=0;for(i=rr[x].size()-1;i>0;--i)Ins(rr[x][i-1]*4-2,rr[x][i]*4-2,0),Ins(rr[x][i]*4,rr[x][i-1]*4,0);for(i=cc[x].size()-1;i>0;--i)Ins(cc[x][i-1]*4-3,cc[x][i]*4-3,0),Ins(cc[x][i]*4-1,cc[x][i-1]*4-1,0);for(i=cc[x].size()-1;~i;--i) tmp[++nn]=-cc[x][i];for(i=rr[x].size()-1;~i;--i) tmp[++nn]=rr[x][i];std::sort(tmp+1,tmp+nn+1,cmp);for(t=1,i=j=0;t<nn;++t) {if(tmp[t]<0)++j,tmp[t]=-tmp[t];else ++i;len=trie.lca(pos[std::abs(tmp[t])],pos[std::abs(tmp[t+1])]);if(i!=0&&j!=cc[x].size())Ins(rr[x][i-1]*4-2,cc[x][j]*4-3,len);if(j!=0&&i!=rr[x].size())Ins(rr[x][i]*4,cc[x][j-1]*4-1,len);}
}
const ll nN=262144,inf=20000000000;
ll d[MM<<2];
struct node{ll x;int f;}t[nN<<1];
inline node Min(const node&o,const node&oo){return o.x<oo.x?o:oo;}
inline void rw(int k,ll x){for(t[k+=nN].x=x;k>>=1;)t[k]=Min(t[k<<1],t[k<<1|1]);}
inline void dij()
{reg int i,x;++tt;for(i=cc[1].size()-1;~i;--i)Ins(tt,cc[1][i]*4-3,0),Ins(tt,cc[1][i]*4-1,0);for(i=1;i<nN<<1;++i) t[i].x=inf;for(i=1;i<=tt;++i) d[t[i+nN].f=i]=inf;for(rw(tt,d[tt]=0);t[1].x!=inf;){rw(x=t[1].f,inf);for(i=hr[x];i;i=e[i].nex)if(d[e[i].to]>d[x]+e[i].w)rw(e[i].to,d[e[i].to]=d[x]+e[i].w);}
}
inline ll getans(int x)
{reg ll i,ans=inf;for(i=rr[x].size()-1;~i;--i)ans=min(ans,min(d[rr[x][i]*4-2],d[rr[x][i]*4]));return ans;
}
inline void init()
{nn=tt=en=idt=0;ME(hr);ME(pos);ME(tmp);ME(dfn);for(reg int i=1;i<=N;++i) rr[i].clear(),cc[i].clear();
}
int main()
{reg int T=read();while(T--) {N=read(),M=read(),K=read();trie.init();reg int i,x,y,c;for(i=1;i<=M;++i) x=read(),y=read(),c=read(),ins(x,y,c,read());for(i=1;i<K;++i) x=read(),y=read(),trie.ins(x,y,read()); trie.build();for(i=2;i<=N;++i) Build(i);dij();for(i=2;i<=N;++i) printf("%lld\n",getans(i));init();}
}Blog来自PaperCloud,未经允许,请勿转载,TKS!