xgboost回归预测模型_偏最小二乘回归分析法 从预测角度对所建立的回归模型进行比较...

在实际问题中,经常遇到需要研究两组多重相关变量间的相互依赖关系,并研究用一组变量(常称为自变量或预测变量)去预测另一组变量(常称为因变量或响应变量), 除了最小二乘准则下的经典多元线性回归分析(MLR),提取自变量组主成分的主成分回归分析(PCR)等方法外,还有近年发展起来的偏最小二乘(PLS)回归方法。
偏最小二乘回归提供一种多对多线性回归建模的方法,特别当两组变量的个数很多,且都存在多重相关性,而观测数据的数量(样本量)又较少时,用偏最小二乘回归建立的模型具有传统的经典回归分析等方法所没有的优点。 偏最小二乘回归分析在建模过程中集中了主成分分析,典型相关分析和线性回归分析方法的特点,因此在分析结果中,除了可以提供一个更为合理的回归模型外,还可以同时完成一些类似于主成分分析和典型相关分析的研究内容,提供更丰富、深入的一些信息。
今天我们学习偏最小二乘回归分析的建模方法;通过例子从预测角度对所建立的回归模型进行比较。
偏最小二乘回归
考虑 p 个变量 y1 , y2 ,... , yp " 与 m 个自变量 x1 , x2 ,... , xm " 的建模问题。
偏最小二乘回归的基本作法是首先在自变量集中提出第一成分 t1 ( t1 是 x1 ,... , xm" 的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分u1 , 并要求 t1 与 u1 相关程度达到最大。然后建立因变量 y1, ..., yp与 t1的回归,如果回归方程已达到满意的精度,则算法中止。否则继续第二对成分的提取,直到能达到满意的精度为止。若最终对自变量集提取 r 个成分 t1 ,t2 ,... ,tr ,偏最小二乘回归将通过建立 y1 ,... , yp 与 t1 ,t2 ,... ,tr 的回归式,然后再表示为 y1 ,... , yp " 与原自变量的回归方程式, 即偏最小二乘回归方程式。
为了方便起见,不妨假定 p 个因变量 y1 ,... , yp 与 m 个自变量 x1 ,... , xm 均为标准化变量。因变量组和自变量组的n 次标准化观测数据阵分别记为
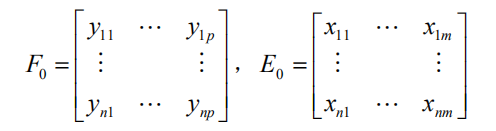
偏最小二乘回归分析建模的具体步骤如下:

(1)分别提取两变量组的第一对成分,并使之相关性达最大。
假设从两组变量分别提出第一对成分为t1 和u1 ,t1 是自变量集 X (x1 ,... , xm )T = 1 的线性组合:
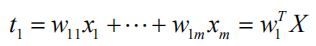
u1 是因变量集
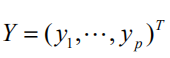
的线性组合:
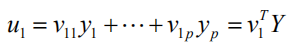
为了回归分析的需要,要求:
① t1 和 u1 各自尽可能多地提取所在变量组的变异信息;
② t1 和 u1 的相关程度达到最大。
由两组变量集的标准化观测数据阵 E0 和 F0 ,可以计算第一对成分的得分向量,记 为 tˆ1 和 uˆ1 :
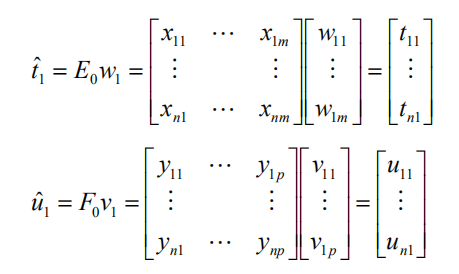
第一对成分 t1 和 u1 的协方差Cov(t1 ,u1 ) , 可用第一对成分的得分向量 tˆ1 和 uˆ1 的内积来计算。故而以上两个要求可化为数学上的条件极值问题:
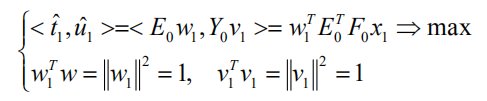
利用Lagrange乘数法,问题化为求单位向量 w1和v1,使
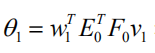
最大。问题的求解只须通过计算 m× m 矩阵
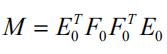
的特征值和特征向量。
且 M 的最大特征值为θ12 ,相应的单位特征向量就是所求的解 w1,而 v1 可由 w1计算得到
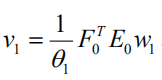
(2)建立 y1 ,... , yp " 对 t1 的回归及 x1 ,... ,xm " 对 t1 的回归。 假定回归模型为
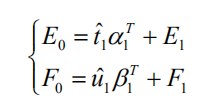
其中
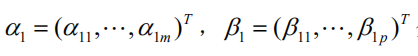
分别是多对一的回归模型中的参数向量, E1和 F1是残差阵。回归系数向量 α1 , β1 的最小二乘估计为
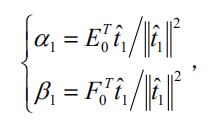
称 α1 , β1 为模型效应负荷量。
(3)用残差阵 E1和 F1代替 E0 和 F0 重复以上步骤。
记
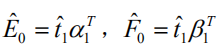
则残差阵
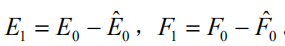
如果残差阵 F1 中元素的绝对值近似为 0,则认为用第一个成分建立的回归式精度已满足需要了,可以停止抽取成分。否则用残差阵 E1和 F1代替 E0 和 F0 重复以上步骤即得:
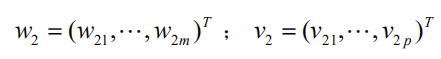
分别为第二对成分的权数。而
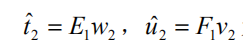
v 为第二对成分的得分向量。
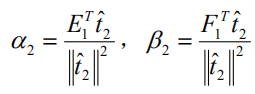
分别为 X ,Y 的第二对成分的负荷量。这时有
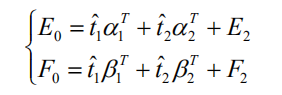
(4)设 n × m 数据阵 E0 的秩为 r ≤ min(n −1,m) ,则存在 r 个成分 t1 ,t2 , ...,tr " , 使得
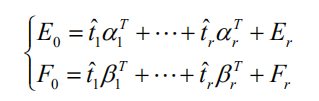
把 tA=wk1x1+...+wkmxm(k=1,2,...,,r)
代入 Y = t1β1 +...+ tr βr ,即得 p 个因变量的偏最小二乘回归方程式
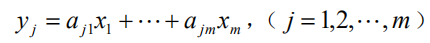
(5)交叉有效性检验。
一般情况下,偏最小二乘法并不需要选用存在的 r 个成分 t1 ,t2 ,... ,tr来建立回归式,而像主成分分析一样,只选用前l个成分(l ≤ r ),即可得到预测能力较好的回归模型。对于建模所需提取的主成分个数l,可以通过交叉有效性检验来确定。
每次舍去第i 个观测(i = 1,2,", n ),用余下的 n −1个观测值按偏最小二乘回归方法建模,并考虑抽取h 个成分后拟合的回归式,然后把舍去的第i 个观测点代入所拟合的回归方程式,得到 yj ( j =1,2,.. , p) 在第i 个观测点上的预测值yˆ(i)j(h) 。对 i = 1,2,..., n 重复以上的验证,即得抽取 h 个成分时第 j 个因变量 yj ( j =1,2,.. , p) " 的预测误差平方和为
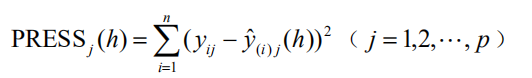
Y= ( y1 ,... , yp ) T的预测误差平方和为
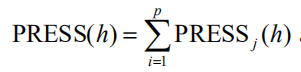
另外,再采用所有的样本点,拟合含h 个成分的回归方程。这时,记第i 个样本点 的预测值为 yijˆ (h) ,则可以定义 yj 的误差平方和为
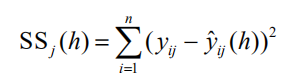
定义Y 的误差平方和为
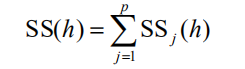
当 PRESS(h) 达到最小值时,对应的 h 即为所求的成分个数。通常,总有PRESS(h) 大于SS(h) ,而SS(h) 则小于SS(h −1)。因此,在提取成分时,总希望比值 PRESS(h) SS(h −1) 越小越好;一般可设定限制值为 0.05,即当
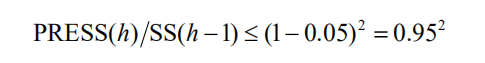
时,增加成分 t h有利于模型精度的提高。或者反过来说,当
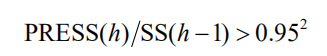
时,就认为增加新的成分 th ,对减少方程的预测误差无明显的改善作用。
为此,定义交叉有效性为
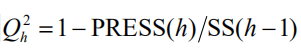
这样,在建模的每一步 计算结束前,均进行交叉有效性检验,如果在第 h 步有
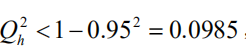
则模型达到精度要求,可停止提取成分;若 Qh2 ≥0.0975 ,表示第h 步提取的 th 成分的边际 贡献显著,应继续第 h +1步计算。
• END •
模友们可能已经发现:现在公众号推送文章的顺序,已经不会按时间排列了。这种变化,可能会让各位模友错过我们每天的推送。
所以,如果你还想像往常一样,聚焦数模乐园,就需要将“数模乐园”标为星标公众号,同时在阅读完文章后,别忘了给一个“在看”哦。
星标步骤
(1)点击页面最上方“数模乐园”,进入公众号主页
(2)点击右上角的小点点,在弹出页面点击“设为星标”,就可以啦。


扫码关注我们

2020国际赛QQ参赛群


球分享

球点赞

球在看
相关文章:

win7的IE缓存,临时文件,cookies和历史记录
2019独角兽企业重金招聘Python工程师标准>>> vista、win7的缓存以及临时文件、Cookies和历史记录都在以下几个地方: 缓存: %userprofile%\AppData\Local\Microsoft\Windows\Temporary Internet Files Temp: %userprofile%\AppData\Local\Temp Cookies: %…

Sql Server函数全解(四)日期和时间函数
阅读目录 1.获取系统当前日期的函数getDate();2.返回UTC日期的函数UTCDATE()3.获取天数的函数DAY(d)4.获取月份的函数MONTH(d)5.获取年份的函数YEAR(d)6.获取日期中指定部分字符串值的函数DATENAME(dp,d)7.获取日期中指定部分的整数值的函数DATEPART(dp,d)8.计算日期和时间的函…

关于python的比赛_【蓝桥杯】——python集团的比赛技巧,Python,组
【蓝桥杯】—— Python组比赛技巧蓝桥杯是大学生IT学科赛事,由工业和信息化部人才交流中心主办,所以对于大学生还说还是非常值得去参加的,2020年第十一届蓝桥杯新增了大学Python组,不分组别,第一届没有历届的真题&…

杭电 HOJ 1312 Red and Black 解题报告
搜索,bfs。依旧用队列做。边界处懒得处理,全部初始化为-1。当然,0也可以。AC代码如下: #include<iostream> #include<deque> using namespace std;struct Point {int x,y; } x,y;int main() {char str[22];int i,j,n,…

pfile和spfile的区别
pfile和spfile的区别 pfile 默认的名称为“init例程名.ora”文件路径:/app/oracle/product/10.2.0/dbs,这是一个文本文件,可以用任何文本编辑工具打开。spfile 默认的名称为“spfile例程名.ora”文件路径:/app/oracle/product/10…

json操作2
import jsonfopen(a.txt,w,encodingutf-8)goods{ 宝马:111111, 奔驰:222222}resjson.dumps(goods,ensure_asciiFalse)#把字典转成jsonf.write(res) json.dump(goods,f,ensure_asciiFalse)#把字典转成json,json会帮你write一次 ----颜色不一样的代码一致运行结果ÿ…

缓冲区和数组的输入输出问题
最近编写程序的时候一直被数据的输入输出所困扰,由此写篇博文总结一下最近遇到的问题和解决方法,错误之处望指正。 1.数组使用的一些语法注意事项 (1)数组的定义 一维数组:类型名 数组名 [常量表达式] 常量表达式中可…

目前python主要应用领域零售_python3读取HDA零售企业数据(一)
#-*- coding:utf-8 -*-# 下载河南FDA各药品经营企业目录import urllib.requestimport urllib.parseimport reimport osimport http.cookiejarheader {Connection: Keep-Alive,Accept: application/x-ms-application, image/jpeg, application/xamlxml, image/gif, image/pjpeg…

调试webservice遇到“测试窗体只能用于使用基元类型作为参数的方法”的解决办法...
之前一直写webservice 没有遇见这种情况,因为一般返回的参数整形 字符串 之类的 都是基本类型,最多也就是把xml序列化为一个字符串返回,这次遇到了返回一个引用类型的,不能直接调试了。所以,现在只能写一个程序把webse…

EJB3.1 JBoss7.1 Eclipse3.7
为什么80%的码农都做不了架构师?>>> EJB3.1 JBoss7.1 Eclipse3.7 ------Hello World 一、环境配置: JDK:正常配置 Eclipse:正常下载,解压(V3.7) JBoss:正常下载…

NOIP2012-摆花
放题目不解释~~~~ 【试题描述】 小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共m盆。通过调查顾客的喜好,小明列出了顾客最喜欢的n种花,从1到n标号。为了在门口展出更多种花,规定第i种花不能…

github提交代码却没有显示绿格子
在github上提交代码之后,进入github上面查看自己的提交,可以看看刚刚的提交内容,但是却一直没有显示绿格子,一个原因是本地git的配置邮箱和github上面的邮箱不一致。 解决办法是,打开本地的git bash,然后直…

spark+openfire即时通讯工具二次开发参考文档
摘自: http://gmd20.blog.163.com/blog/static/168439232010527525542/ 其中Spark是开源的基于XMPP协议的即时通讯工具,公司最近也换到用这个了,说是在服务器(openfire)上可以备份消息,然后可以看员工的聊天记录 smac…

python selenium 等待页面加载完毕_Selenium_等待页面加载完毕
隐式等待WebDriver driver newFirefoxDriver();driver.get("www.baidu.com");driver.manage().timeouts().implicitlyWait(20, TimeUnit.SECONDS);WebElement element driver.findElement(By.cssSelector(".abc"));((JavascriptExecutor)driver).executeS…

TechEd 2012奥兰多!
亚特兰大TechEd 2011如同昨天的事情,今天又无比期待奥兰多的TechEd 2012!如果可能的话,我将继续为大家分享关于奥兰多TechEd 2012 的现场见闻! 转载于:https://blog.51cto.com/suhua/845796

【常见CPU架构对比】维基百科
Comparison of instruction set architectures https://en.wikipedia.org/wiki/Comparison_of_instruction_set_architectures转载于:https://www.cnblogs.com/timeObjserver/p/9441242.html

Python基础学习1(Python的Windows和Linux的安装及简单学习)
一Python的安装 1.Windows下安装Python (1)windows 命令行的几个常见的命令 dir:查看当前目录下的所有文件,以及目录 cd NAME:进入到NAME目录下(tab键自动补全) D: 切换到D盘 type NUL…

Python Tutorial(十):浏览标准库(一)
10.1 操作系统接口 os模块提供很多函数用于和操作系统的交互: 确定使用import os风格而不是from os import *。这将避免os.open()被内建的open()函数遮住,它的操作截然不同。 内建的函数dir()和help()作为交互助手对于大的模块像os是非常有用的ÿ…

学业水平考试b能上985吗_河南单招哪些学院好考?哪些专业能录取?
高职单招的录取规则是什么?在符合报考条件的前提下,考试是由两部分组成:文化素质评价职业适应性测试、职业技能测试。文化素质评价大多院校采用学业水平考试等级成绩折合一定的分值计入。有些学校采用现场考试语数外三门,以实际成绩计入。职…

单例模式Java实现
为什么80%的码农都做不了架构师?>>> public class Singleton {private static Singleton instance null;// 同步时加锁的静态对象private static final Object OL new Object();private Singleton() {// Class initialize}/** 在多线程环境下执行时的…

Go环境搭建、Sublime Text 3 安装Go语言相关插件gosublime
Go 语言环境安装 1.brew install go 默认安装,被安装了/usr/local/Cellar/go 目录并自设置了环境变量。 2.go env 可查看目前的go的环境变量 3.配置一个GOPATH环境变量,是工作目录。 根据约定,GOPATH下需要建立3个目录: bin 存储编…

ABAP性能实例七例
一、SQL Interface 1.Select ... Where vs. Select Check 用Select … Where语句效率比Select Check语句要高,例如: SELECT * FROM SBOOK INTO SBOOK_WA WHERE CARRID LH AND CONNID 0400. ENDSELECT. SELECT * FROM SBOOK INTO SBOOK_WA. CHECK: SB…

C语言中打印‘%’
C语言中打印‘%’不能直接printf("%"),这里的%有特殊含义的,要想打印的话,需要输入printf("%%"),两个%才可以将它打印出来。C语言中的其他的特殊字符,以后再慢慢做整理。

vba 字体颜色_多掌握一些VBA语句,让自己书写代码更加顺畅
VBA 是好东西,对于身在职场的人员,或者是积极打拼的创业者,是数据分析的首选,他可以实现量身定做,解决一些规律性强的问题。或者代替人处理一些可以描述出有逻辑关系的数据分析。多掌握一些VBA语句,让自己书…

编写jQueryUI插件(widget)
使用jQueryUI的widget来写插件,相比于基本的jquery插件有一些好处: * 方便实现继承,代码重用 * 默认是单例 * widget已经给你实现好的一些常用方法,例如destroy 带来好处的同时也带来了荆棘和陷阱,本文的目的就是梳理这…

mail 发送email
(一)首先安装ssmpt和mailutils: sudo apt-get install ssmtp mailutils (二)接下来编辑配置文件sudo gedit /etc/ssmtp/ssmtp.conf rootYOUR_PERSONAL_MAILDOMAIN mailhubsmtp.gmail.com:465 rewriteDomaingmail.com A…

C语言中字符型在计算机中的存储
一. 字符型的分类和表示范围 char:是有符号还是无符号数视编译器而定,一般为有符号数,下文把它全部当成有符号数进行讨论 表示范围:32位和64位机器上均是一个字节,所以是八个bit位,最高位为符号位之后&…

python中正确的表达式_python中如何正确使用正则表达式的详细模式(Verbose mode expression)...
简单介绍正则表达式并不是Python的一部分。正则表达式是用于处理字符串的强大工具,拥有自己独特的语法以及一个独立的处理引擎,效率上可能不如str自带的方法,但功能十分强大。得益于这一点,在提供了正则表达式的语言里,…

ASP.NET中 RequiredFieldValidator(非空验证)的使用
ylbtech-ASP.NET-Control-Validator: RequiredFieldValidator(非空验证)的使用ASP.NET中 RequiredFieldValidator(非空验证)的使用。 1.A,运行效果返回顶部 登录 RequiredFieldValidator:非空验证重要的属性:1,ControlToValidate:要验证的控件…

5013.FortiGate企业级硬件防火墙Demo演示文档
FortiGate企业级硬件防火墙Demo演示文档 语言:英文类型:Demo大小:2MB格式:WEB摘要:和真实的硬件防火墙操作界面一模一样的,非常实用!可以通过这些界面了解到在配置硬件防火墙时需要配置哪些参数…
