算法模板之双链表图文详解
文章目录
一. ⛳️使用数组模拟双链表讲解
1.1 🔔为什么我们要使用数组去模拟双链表?
由于该问题已经在第一期《算法模板之单链表讲解》这篇文章中已经叙述过了,相信看过第一期的小伙伴应该已经知道,在这里就不多阐述,感兴趣的小伙伴可以自行跳转浏览。
1.2 🔔用数组模拟实现双链表
1.2.1 👻整体框架说明
初始状态:左边界结点指向右边界结点,右边界结点指向左边界结点

插入结点状态:
- 创建数组
val、pre和ne分别存储某个结点的值以及它的前驱指针和后继指针; - 下标 0 和 1 分别存储边界结点;
- 从下标 2 的位置开始插入结点;
- 本文仅仅使用左右边界结点的指针,无需在意其中存的值。
综上所述,真正的结点相当于从下标为2的位置开始往后所有插入的数,左右边界结点仅起到一个指针的效果。如下图的3,4,5,6为真正的结点。

1.2.2 👻双链表查找和修改
因为是使用数组模拟出来的链表,所以对于查找和修改直接通过数组下标进行遍历查找即可,这里就不多叙述。
1.2.3 👻双链表插入结点
在第k个结点的右边插入一个数 x:如下图在第2个结点后面插入一个数 7。

代码展示(建议结合图示看注释):
//在结点k的右边插入一个数x
void insert(int k, int x)
{
//将待插值赋给新结点
val[idx] = x;
//将新结点分别指向插入位置的右结点和左结点
ne[idx] = ne[k];
pre[idx] = k;
//将新结点的右边结点向左指向新结点
pre[ne[k]] = idx;
//将新结点的左边结点向右指向新结点
ne[k] = idx;
//更新结点索引
idx++;
}
其他形式插入:在链表的最左端插入、最右端插入、在第k个结点的左边插入一个数 x
在其他位置插入,大家可以按照上面的方式自行模拟。不过,在算法竞赛中如果每种插入方式都模拟一下,显然是太浪费时间了。仔细观察可以发现,我们仍然可以使用上面的insert(int k, int x)函数实现各种位置的插入,只需要稍微变动一下传入的 k 值。
- 在第k个结点的左边插入一个数 x: 如下图,在第2个结点的左边插入一个数7,可以转化为在第1个结点后面插入一个数7,执行语句:
insert(pre[k], x)即可。

- 在链表的最左端插入一个数x: 如下图,在最左端插入一个数x,可以转化为在左边结点后面插入一个数x,执行
insert(0, x)即可。

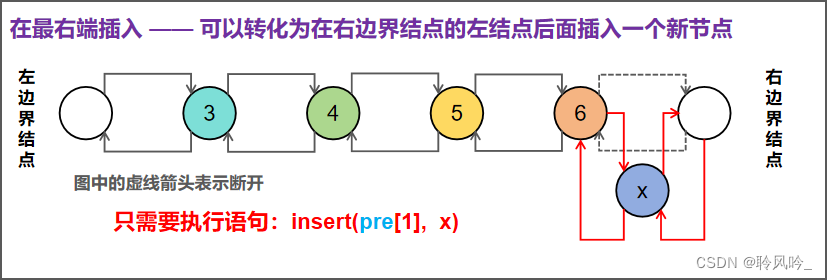
- 在链表的最右端插入一个数x: 如下图,在最右端插入一个数x,可以转化为在右边界结点的左结点后面插入一个数x,执行
insert(pre[1], x)即可。
1.2.4 👻双链表删除结点
删除第k个结点

代码展示(建议结合图示看注释):
//删除第k个结点
void remove(int k)
{
//将待删除结点的左结点的后继指针指向待删除结点的右结点
ne[pre[k]] = ne[k];
//将待删除结点的右结点的前驱指针指向待删除结点的左结点
pre[ne[k]] = pre[k];
}
1.3 🌟模板提取(重点)🌟
1.3.1 👻有详细注释版
模板代码
// val[i] 表示结点i的值
// pre[i] 表示结点i的前驱指针
// ne[i] 表示结点i的后继指针
// idx 存储当前已经用到了哪个点,即记录当前下标位置
int val[N], pre[N], ne[N], idx;
//初始化
void init()
{
//左边界结点指向右边界结点,右边界结点指向左边界结点
ne[0] = 1;
pre[1] = 0;
//更新结点索引,因为下标0和1被左右边界结点占用。
idx = 2;
}
//在结点k的右边插入一个数x
//只使用本函数可以通过改变k的值,实现其他形式的插入。
void insert(int k, int x)
{
//将待插值赋给新结点
val[idx] = x;
//将新节点分别指向插入位置的右结点和左结点
ne[idx] = ne[k];
pre[idx] = k;
//将新结点右边一节点向左指向新结点
pre[ne[k]] = idx;
//将新结点左边一节点向右指向新结点
ne[k] = idx;
//更新结点索引
idx++;
}
//删除第k个结点
void remove(int k)
{
//将待删除结点的左结点的后继指针指向待删除结点的右结点
ne[pre[k]] = ne[k];
//将待删除结点的右结点的前驱指针指向待删除结点的左结点
pre[ne[k]] = pre[k];
}
1.3.1 👻无详细注释版
int val[N], pre[N], ne[N], idx;
//初始化
void init()
{
ne[0] = 1;
pre[1] = 0;
idx = 2;
}
//在结点k的右边插入一个数x
void insert(int k, int x)
{
val[idx] = x;
ne[idx] = ne[k];
pre[idx] = k;
pre[ne[k]] = idx;
ne[k] = idx;
idx++;
}
//删除第k个结点
void remove(int k)
{
ne[pre[k]] = ne[k];
pre[ne[k]] = pre[k];
}
二. ⛳️题目练习
2.1 题目

2.2 输入样例
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
2.3 输出样例
8 7 7 3 2 9
2.4 c++代码
#include<iostream>
using namespace std;
const int N = 100010;
int val[N], pre[N], ne[N], idx;
//初始化
void init()
{
ne[0] = 1;
pre[1] = 0;
idx = 2;
}
//在结点k的右边插入一个数x
void insert(int k, int x)
{
val[idx] = x;
ne[idx] = ne[k];
pre[idx] = k;
pre[ne[k]] = idx;
ne[k] = idx;
idx++;
}
//删除第k个结点
void remove(int k)
{
ne[pre[k]] = ne[k];
pre[ne[k]] = pre[k];
}
int main()
{
int m;
cin >> m;
init();//切记:不要忘记进行初始化
while(m--)
{
int k, x;
string op;
cin >> op;
//判断执行哪种操作
if(op == "L")//在链表的最左端插入x
{
cin >> x;
insert(0, x);
}
else if(op == "R")//在链表的最右端插入x
{
cin >> x;
insert(pre[1], x);
}
else if(op == "D")//把第k个插入的数删除
{
cin >> k;
remove(k+1);//因为初始化从下标为2位置开始插入结点,所以第k插入数的下标为k+2-1
}
else if(op == "IL")//第k个插入的数左侧插入一个数
{
cin >> k >> x;
insert(pre[k+1], x);
}
else//第k个插入的数右侧插入一个数
{
cin >> k >> x;
insert(k+1, x);
}
}
//打印链表
for(int i = ne[0]; i != 1; i = ne[i]) cout << val[i] << " ";
cout << endl;
return 0;
}
相关文章:

Windows下配置最新ChromeDriver
选择与操作系统相对应的版本进行下载,并且与谷歌安装目录安装在同一位置,注意http status要为200才是正常可用。本例中,我的Chrome版本是120.0.6099.110,下载版本120.0.6099.71,可以正常使用。可以看到,当前chrome是最新版本:120.0.6099.110(正式版本) (64 位)。意思就是说:你的Chrome版本是118,但你的ChromeDriver版本是114。点击系统变量中的path,点击新增,并将chrome的安装目复制填入后,点击确定。

讲解torch扩展维度
本文讲解了通过和两个函数来扩展张量的维度。这对于深度学习中的形状变换和维度操作非常有用。函数在指定位置插入一个新维度,返回一个新的张量;而函数是一个原地操作,直接修改原始张量。在使用时,需要根据具体需求选择适合的函数,并小心处理原地操作带来的影响。希望本文能够帮助你理解和使用和函数,并在深度学习中能够灵活应用。更多关于PyTorch的形状变换和张量操作,请参考PyTorch官方文档。

讲解nginx.pid“ failed (2: The system cannot find the file specified
该脚本首先检查Nginx进程是否在运行,如果未运行则尝试重新生成"nginx.pid"文件,并启动Nginx服务。然后,脚本会启动Nginx服务。通过使用该脚本,你可以自动处理"nginx.pid" failed 错误,并重新生成所需的"nginx.pid"文件。nginx.pid 文件是Nginx Web服务器在运行过程中生成的一个文件,用于存储Nginx主进程的进程ID(PID)。它表明Nginx无法找到指定的"nginx.pid"文件,这个文件用于存储Nginx主进程的进程ID(PID)。

讲解pytho作线性拟合、多项式拟合、对数拟合
综上所述,Matplotlib 是一个功能强大且灵活的可视化库,可以帮助我们轻松创建各种类型的图形,并对其进行定制和调整,以满足不同的需求。通过使用Python的numpy和matplotlib库,我们可以轻松实现线性拟合、多项式拟合和对数拟合。拟合(Fitting)是数据分析中常用的一种方法,它可以根据已有的数据,找到最适合这些数据的函数模型。Python提供了丰富的库和工具,可用于进行线性拟合、多项式拟合和对数拟合。假设我们有一组测量的物理实验数据,我们希望通过多项式拟合来拟合出一个近似的曲线。

讲解nvcc fatal : A single input file is required for a non-link phase when an outputfile is specified
在使用nvcc编译和链接CUDA代码的过程中,要避免"nvcc fatal: A single input file is required for a non-link phase when an output file is specified"错误,你需要明确指定编译阶段和链接阶段的输入文件,并将它们分别与相关选项放在一起。这样做可以确保nvcc命令正确处理你的代码,并生成所需的输出文件。希望本文能够帮助你解决这个常见的错误,并更顺利地进行CUDA开发和GPU加速编程。

讲解device:GPU:0 but available devices are [ /job:localhost/replica:0/task:0/dev
这个错误通常由于 GPU 驱动程序、CUDA 库、环境变量配置或访问权限问题导致。通过检查安装、配置和访问权限,并尝试适当的解决方法,您应该能够解决此问题,使代码能够在 GPU 上正常运行。深度学习框架的 GPU 加速是提高模型训练和推断效率的重要手段,因此解决这些配置问题对于实现更快的深度学习任务至关重要。希望本文对您解决此类问题时能够提供指导和帮助。

Mybatis概述和快速入门
(1)Mybatis是一个半ORM(对象关系映射)框架,它内部封装了JDBC,开发时只需要关注SQL语句本身,不需要花费精力去处理加载驱动、创建连接、创建statement等繁杂的过程。程序员直接编写原生态sql,可以严格控制sql执行性能,灵活度高。(2)MyBatis 可以使用 XML 或注解来配置和映射原生信息,将 POJO映射成数据库中的记录,避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。

讲解异常: cv::Exception,位于内存位置 0x00000059E67CE590 处
在使用OpenCV进行图像处理和计算机视觉任务时,异常是一种常见的异常情况,通常由于内存分配失败引起。在解决该异常时,我们应该考虑增加系统可用内存、优化算法和数据集,以及检查代码中的内存管理问题。通过这些方法,我们可以更好地处理异常,提高系统的稳定性和性能。希望本文能够帮助您理解和解决异常,并顺利进行OpenCV图像处理和计算机视觉任务。

讲解PyTorch 多分类损失函数
交叉熵损失函数和负对数似然损失函数是常用的多分类损失函数,根据具体的问题和需求选择合适的损失函数对模型进行训练和优化。然后,我们使用预训练的ResNet模型作为基础模型,将最后一层的全连接层替换为一个具有10个输出节点的线性层,以适应我们的分类任务。在实际应用中,您可以根据具体的场景和需求,选择适合的模型和损失函数,并根据需要进行相应的调整和优化。通过不断尝试和实践,您将能够选择最适合您的多分类问题的损失函数。为了对多分类问题进行有效的训练,我们需要使用适当的损失函数来度量模型预测与真实标签之间的差异。

讲解OpenCV对图像的光照归一化处理
光照归一化是图像处理中重要的预处理步骤之一,可以提高图像可视性和分析结果。在OpenCV中,我们可以使用直方图均衡化和自适应直方图均衡化这两种方法来实现光照归一化处理。希望通过本文的介绍,读者对OpenCV中的光照归一化处理有更深入的理解,并能在实际应用中灵活运用。如果你对OpenCV的图像处理还有更多兴趣,建议阅读OpenCV官方文档和相关教程,进一步探索其丰富功能和应用场景。

【Flink】官宣|Apache Flink 1.17 发布公告
仅供自己学习。因为我们开始用Flink 17了。Apache Flink PMC(项目管理委员)很高兴地宣布发布 Apache Flink 1.17.0。Apache Flink 是领先的流处理标准,流批统一的数据处理概念在越来越多的公司中得到认可。得益于我们出色的社区和优秀的贡献者,Apache Flink 在 Apache 社区中一直保持着快速增长,并且是最活跃的社区之一。

【Flink】字节跳动 Flink 基于 Slot 的资源管理实践
总体上来讲,Flink 整个资源管理、申请和分配围绕 Slot 展开,同时每个 TaskManager 中的 Slot 数量决定了作业在该 TaskManager 中运行的并发计算任务数量。本篇文章主要介绍了 Slot 对资源分配、释放以及计算执行的影响,希望可以帮助大家更好地决策每个 TaskManager 中的 Slot 数量,对 Flink 作业进行调优。
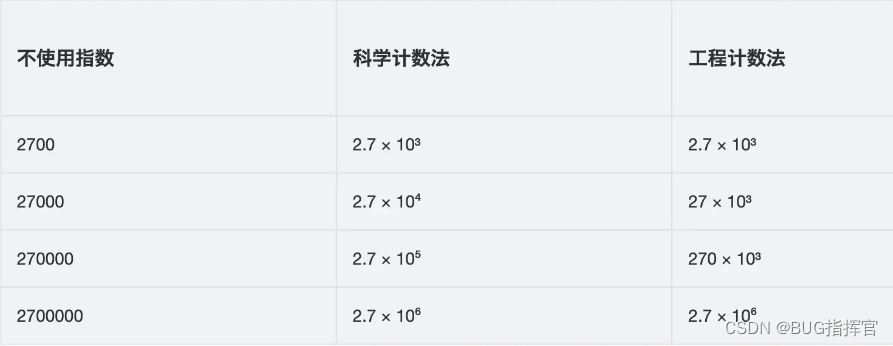
BigDecimal与Double的区别和使用场景
Java在java.math包中提供的API类BigDecimal,用来对超过16位有效位的数进行精确的运算。双精度浮点型变量double可以处理16位有效数,但在实际应用中,可能需要对更大或者更小的数进行运算和处理。一般情况下,对于不需要准确计算精度的数字,可以直接使用Float和Double处理,但是Double.valueOf(String) 和Float.valueOf(String)会丢失精度。所以如果需要精确计算的结果,则必须使用BigDecimal类来操作。

【Flink】如何在 Flink 中规划 RocksDB 内存容量?
主要是自己学习。本文描述了一些配置选项,这些选项将帮助您有效地管理规划 Apache Flink 中 RocksDB state backend 的内存大小。在前面的文章 [1] 中,我们描述了 Flink 中支持的可选 state backend 选项,本文将介绍跟 Flink 相关的一些 RocksDB 操作,并讨论一些提高资源利用率的重要配置。

【redis】redis的哨兵Sentinel高可用架构
redis的哨兵Sentinel高可用架构,redis 哨兵集群与redis集群的关系以及故障转移,故障检测等原理
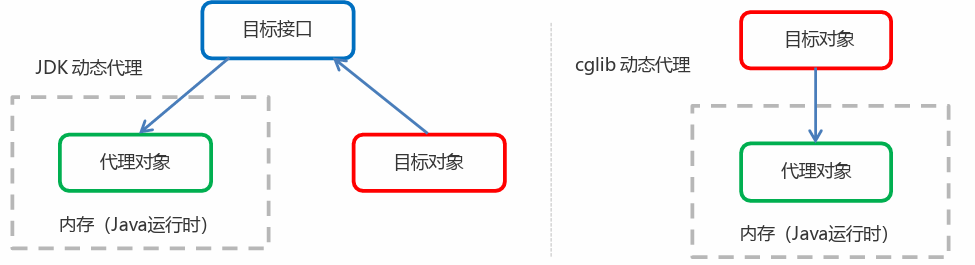
spring 笔记九 Spring AOP
AOP 为Aspect Oriented Programming 的缩写,意思为面向切面编程,是通过预编译方式和运行期动态代理实现程序功能的统一维护的一种技术。AOP 是OOP 的延续,是软件开发中的一个热点,也是Spring框架中的一个重要内容,是函数式编程的一种衍生范型。利用AOP可以对业务逻辑的各个部分进行隔离,从而使得业务逻辑各部分之间的耦合度降低,提高程序的可重用性,同时提高了开发的效率。 作用:在程序运行期间,在不修改源码的情况下对方法进行功能增强。

spring 笔记十 Spring事务管理
Spring 的声明式事务顾名思义就是采用声明的方式来处理事务。这里所说的声明,就是指在配置文件中声明,用在Spring 配置文件中声明式的处理事务来代替代码式的处理事务。声明式事务处理的作用 事务管理不侵入开发的组件。具体来说,业务逻辑对象就不会意识到正在事务管理之中,事实上也应该如此,因为事务管理是属于系统层面的服务,而不是业务逻辑的一部分,如果想要改变事务管理策划的话,也只需要在定义文件中重新配置即可。

C++会搜索的二叉树(BSTree)
本片文章主要介绍了二叉搜索树,并模拟实现!!!

C++继承后的多态 | 抽象类
本片文章介绍了继继承之后的多态和抽象类!!!

算法模板之单链表图文讲解
本文主要讲解单链表模板,文中附有图文讲解,希望对你的算法学习有一定的帮助。
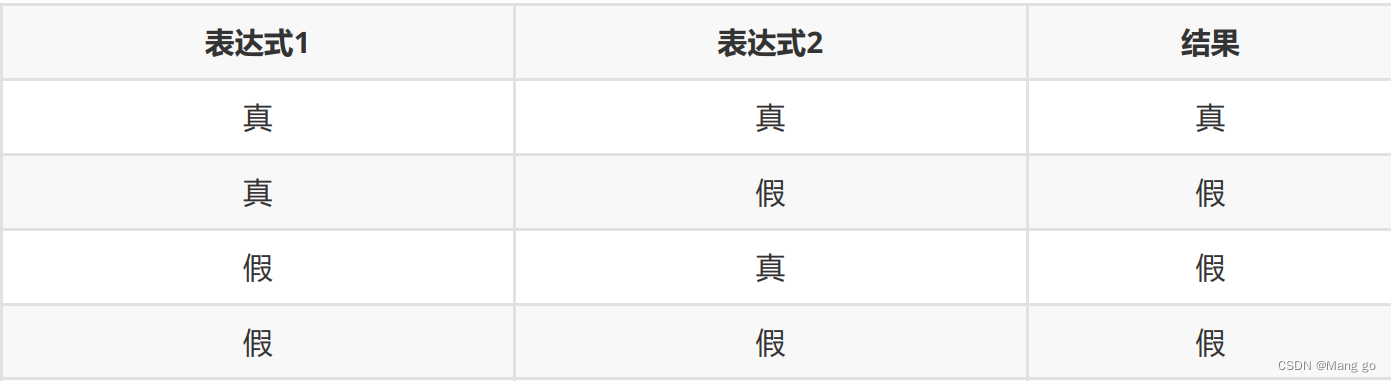
Java运算符及运算符的优先级【超详细】
int a = 10;int b = 20;a + b;a < b;对操作数进行操作时的符号,不同运算符操作的含义不同。作为一门计算机语言,Java也提供了一套丰富的运算符来操纵变量。Java中运算符可分为以下:算术运算符(+ - */)、关系运算符(< > ==)、逻辑运算符、位运算符、移位运算符以及条件运算符等,接下来我们来一个一个介绍。

Java中Jar包部署nohup后台启动定时按日期分割日志
在JAVA开发中很多没有用docker部署,而是选择传统的Jar包部署方式,这样就涉及日志的产生,如果直接部署日志文件会越来越大,程序怎么可能不出现问题,这样打开日志文件就会很慢,不方便后续问题的定位和解决。这样就要采取优化方案,对日志进行分割,这样便于查看。

Java Comparator多属性排序
自然排序通常情况跟equals保持一致,e1,e2是类C的元素,如果e1.compareTo(e2) == 0 那么e1和e2 equals的结果也是true。因为有的时候它俩结果一致,比如刚好就只有一个属性排序的时候,但多数情况下,二者是不一致的。比如有多个排序属性的时候。有的时候获取的数据需要在内存排序,需要根据List中T对象的属性p1,p2,p3等进行排序,该怎么写呢?这种规则掌握了,管它几个属性排序,管它什么升序降序,通通解决。多个属性,按不同的升降序规则,就变的非常简单了,只需要在下面的。
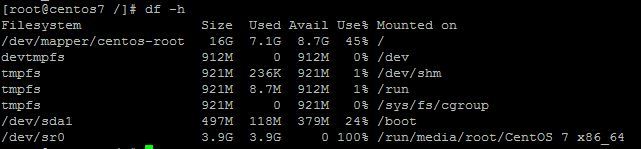
Linux 查看磁盘空间
Linux 查看磁盘空间可以使用 df 和 du 命令。
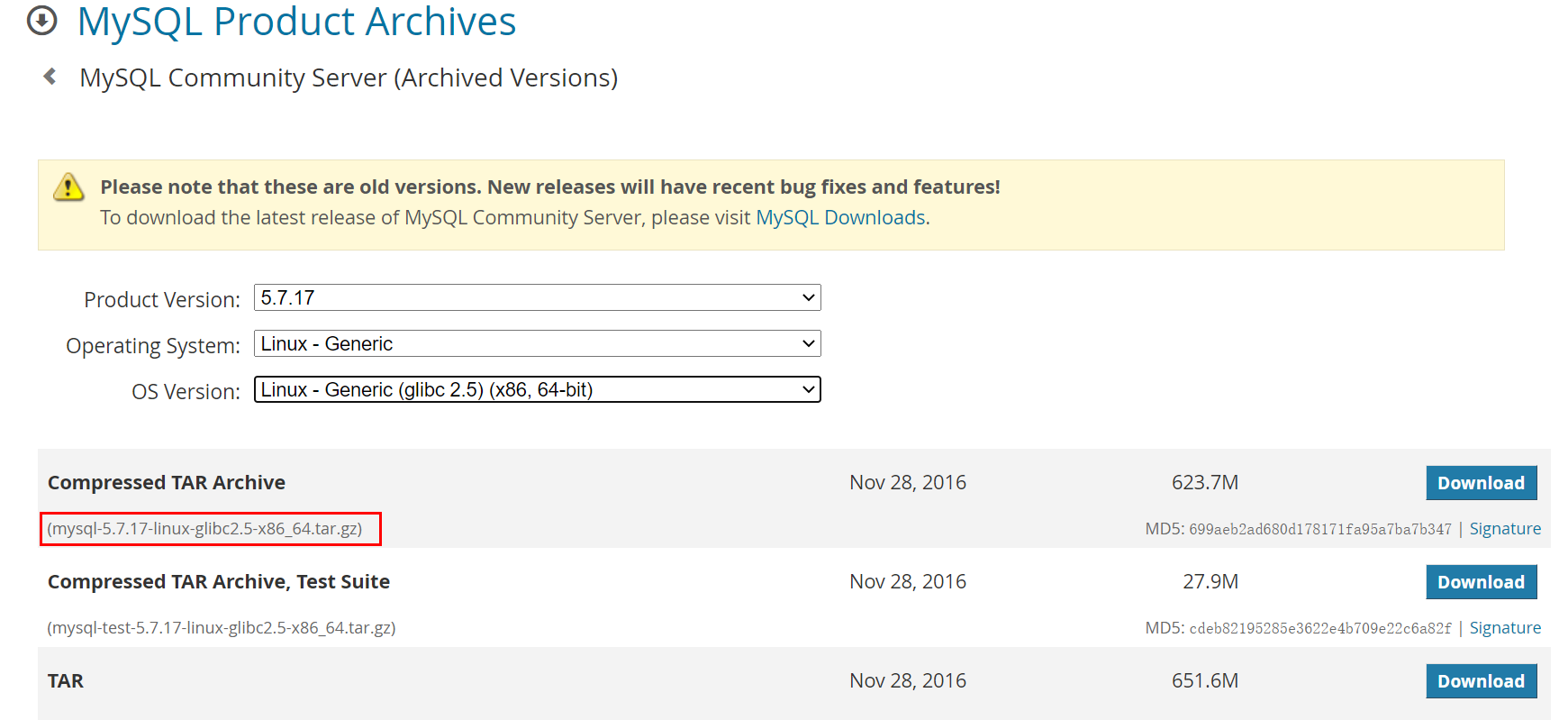
Linux多种方法安装MySQL
源码安装:优点是安装包比较小,只有十多M,缺点是安装依赖的库多,安装编译时间长,安装步骤复杂容易出错。使用官方编译好的二进制文件安装:优点是安装速度快,安装步骤简单,缺点是安装包很大,300M左右。yum安装。rpm安装。

Linux中mysql 默认安装位置&Linux 安装 MySQL
MySQL在Linux系统上的默认安装位置是目录。这是MySQL服务器的数据目录,包含所有数据库文件。通过检查MySQL二进制文件的路径,我们可以确认MySQL是否正确安装。在目录中,MySQL使用一系列文件和子目录来组织和存储数据。确保理解MySQL数据目录的结构对于管理和维护MySQL数据库至关重要。按照顺序安装即可解决。

Linux使用systemd服务和crontab实现Shell脚本开机自动运行&编辑当前用户或者指定用户的crontab内容crontab -e
systemd是Linux系统中的一个初始化系统和服务管理器。它可以用于在系统启动时自动运行Shell脚本。crontab是一个用于定时执行任务的工具。我们可以通过编辑crontab文件来设置开机自启动。
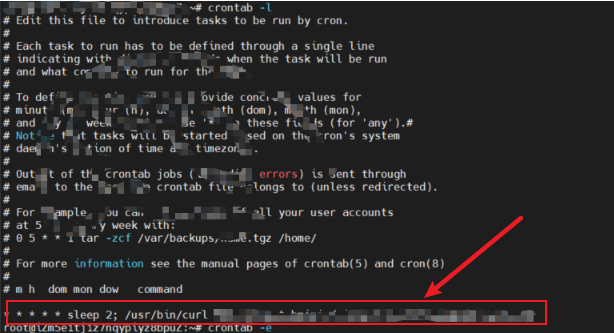
Linux定时任务详解&crontab -e 编辑之后如何保存并退出(Ubuntu)
Linux定时任务是一种可执行的命令或者脚本,在特定的时间或者时间间隔下自动执行。通过在系统中预设一些需要执行的任务,可以让Linux定时任务自动执行并完成这些任务。定时任务可以用于自动备份、系统清理、监控、自动化维护等任务。在Linux中,常用的定时任务程序有系统自带的cron和at命令。其中,cron是一个强大的定时任务工具,可以按照设定的实际时间执行命令,非常常用。anacron最小检测周期是天,使用anacron管理的定时任务应该最小是每隔一天执行。

nginx常用操作命令
都启动了同一个Nginx进程。不一样的是:1、Systemd 是一系列工具的集合,其作用也远远不仅是启动操作系统,它还接管了后台服务、结束、状态查询。2、Systemd更方便作服务管理,启动管理Nginx更佳方便。3、Systemd可以作开机服务管理,让服务跟随系统启动。

linux配置nginx开机自启&nginx部署与systemctl控制启动&/etc/systemd/system 和 /lib/systemd/system 的区别
目录/lib/systemd/system 以及/usr/lib/systemd/system 其实指向的是同一目录,在/目录下执行命令lltotal 28该目录中包含的是软件包安装的单元,也就是说通过 yum、dnf、rpm 等软件包管理命令管理的 systemd 单元文件,都放置在该目录下。/etc/systemd/system/(系统管理员安装的单元, 优先级更高)在一般的使用场景下,每一个 Unit(服务等) 都有一个配置文件,告诉 Systemd 怎么启动这个 Unit。
