C++会搜索的二叉树(BSTree)
目录
前言:
在C语言的数据结构期间我们介绍过二叉树的一些概念;并且实现了其链式结构和实现了前、中、后序的遍历;有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻烦。因此本节借二叉树搜索树,对二叉树部分进行收尾总结。并且后面的map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构;二叉搜索树的特性了解,有助于更好的理解map和set的特性。
二叉搜索树
二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

二叉搜索树操作
二叉搜索树的中序遍历根据其存储结构是排好序的。
- 如果左边存储比根小的数字右边存储比根大的数字,中序遍历的结果是升序的;
- 如果左边存储比根大的数组右边存储比根小的数字,中序遍历的结果是降序的;
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
注意:二叉搜索树是没有“修改”的,因为如果随便修改一个数据,整棵树都要重新去实现。
二叉搜索树的查找
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到空,还没找到,这个值不存在。
注意:
二叉搜索树有一个特别重要的特点:树中没有两个相同的元素。
二叉搜索树的插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点

二叉搜索树元素的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
- 要删除的结点无孩子结点
- 要删除的结点只有左孩子结点
- 要删除的结点只有右孩子结点
- 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况1可以与情况2或者3合并起来,因此真正的删除过程
如下:
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
二叉搜索树的实现
BSTree结点
节点中包含两个该节点类型的指针,分别代表着指向左右孩子和节点中存储的值。
template <class K>
struct BSTNode
{
BSTNode<K>* _left;
BSTNode<K>* _right;
K _key;
//结点的构造函数
BSTNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{
}
};BSTree框架
成员变量为结点类型的指针。
template<class K>
class BST
{
typedef BSTNode<K> Node;
private:
Node* _root=nullptr;
};拷贝构造函数和无参构造函数
因为我们自己写了拷贝构造函数,所以编译器不会默认生成无参构造函数。在C++11中可以让默认构造函数等于default,让编译器再次自动生成默认构造函数。
拷贝一个二叉搜索树开始要使用递归进行调用的。
BST() = default;
BST(const BST<K>& st)
{
_root=Copy(st._root);
}析构函数
因为我们在类外面显示调用根节点很麻烦,直接在类内部以根节点为参数直接递归实现。
public:
~BST()
{
Destory(_root);
}
private:
void Destory(Node*& root)
{
if (root == nullptr)
{
return;
}
Destory(root->_left);
Destory(root->_right);
delete root;
root = nullptr;
}
赋值重载(operator=)
swap函数是库std中的函数,深拷贝;
BST<K>& operator=(BST<K> t)
{
swap(_root, t._root);
return *this;
}插入Insert ()
非递归版本
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else if (parent->_key > key)
{
parent->_left = cur;
}
}
- 首先还是要判断传入的根结点是否为空,如果为空直接开辟一个新的结点即可;
- 如果不为空,先创建一个父亲的结点便于插入的时候做修改;然后在创建一个结点从根节点开始根据二叉搜索树的特点开始找适合插入的位置,当找到时开辟一个新的结点,然后让合适位置的根节点指向开辟好的新节点即可;
递归版本
pbulic:
bool InsertR(const K & key)
{
return _InsertR(_root, key);
}
private:
bool _InsertR(Node*& root,const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
这里的递归也是根据二叉搜索树左右两边孩子的特点巧妙使用引用来实现的,每次递归的参数为上一个根节点指向左孩子或者右孩子的引用,去掉了记录父亲节点。
查找Find()
非递归版本
也是根据二叉搜索树左右孩子的特点实现的。如果查找的值比根结点的值大则和根节点的右孩子比较,反之;
注意:搜索二叉树中是没有两个相同的值的。
bool find(const K& key)
{
if (_root == nullptr)
{
return false;
}
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}递归版本
public :
bool FindR(const K & key)
{
return _FindR(_root, key);
}
private :
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _FindR(_root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
删除()
非递归版本
删除这里的情况还比较复杂,先要根据上面查找函数的思路找到结点;
- 如果左孩子为空,且该结点为父节点的左孩子,则让父节点指向的左孩子为该节点的右支;删掉此节点。如果该结点为父节点的右孩子,则让父节点指向的右孩子为该节点右支;删掉此节点。
- 如果右孩子为空,且该节点为父节点的左孩子,则让父节点指向的左孩子为该节点的右支;删掉此节点。如果该节点为父节点的右孩子,则让父节点指向的左孩子为该节点的左支;删掉此节点。
- 如果左右孩子都不为空,则要取左支最大的(最右结点)或者取右支最小的(最左结点),这里实现的是取右支最小的;先进入该结点的右边,然后使用循环找到最左结点;对该节点和其父节点的值进行交换,然后按照上面左孩子为空调整其父节点指向的孩子结点。然后删除结点。
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//左为空
if (cur->_left == nullptr)
{
//删除根节点的值
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else if (parent->_right == cur)
{
parent->_right = cur->_right;
}
}
delete cur;
}
//右为空
else if (cur->_right == nullptr)
{
//删除根节点的值
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else if (parent->_right == cur)
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
//右树的最小值
Node* subleft = cur->_right;
Node* parent = cur;
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->_key, subleft->_key);
if (subleft == parent->_left)
{
parent->_left = subleft->_right;
}
else
{
parent->_right = subleft->_right;
}
delete subleft;
}
return true;
}
}
return false;
}递归版本
public:
bool EraseR(const K&key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
if (root->_left == nullptr)
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else
{
Node* subleft = root->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
swap(root->_key, subleft->_key);
return _EraseR(root->_right, key);
}
}
}中序遍历
public:
void Inorder()
{
_Inorder(_root);
cout << endl;
}
private:
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}
二叉搜索树的应用
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
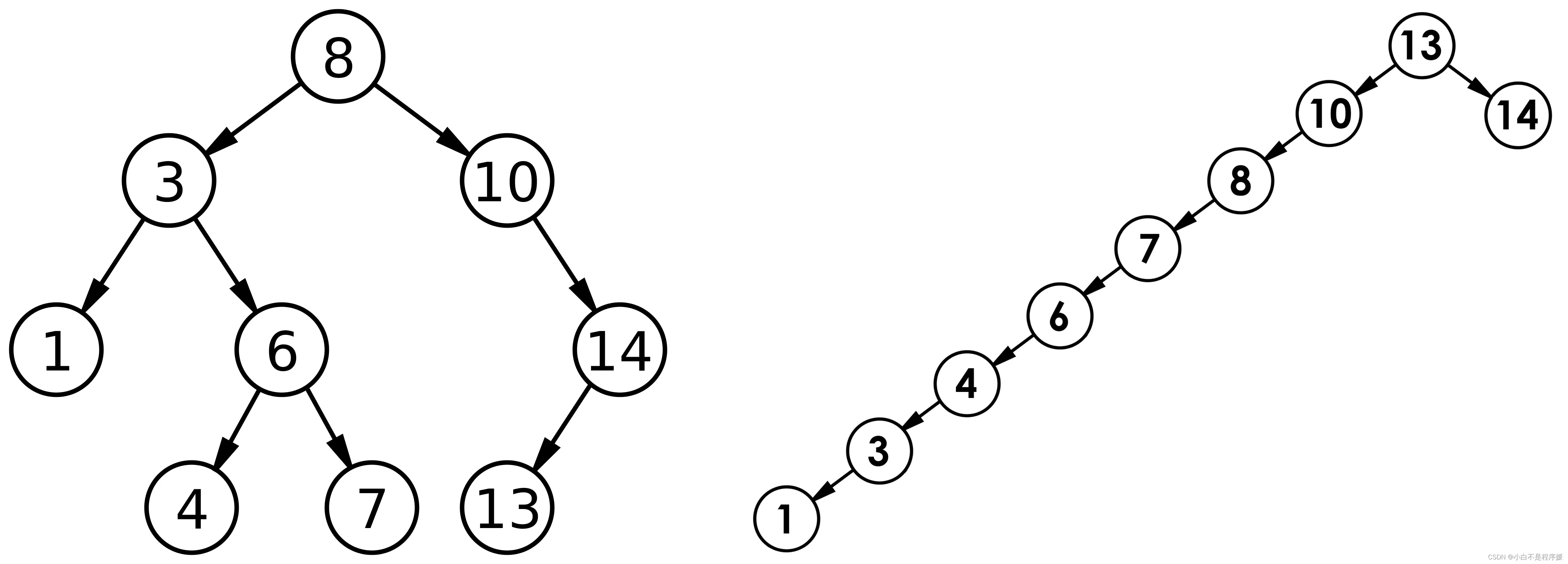
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:O(logN)
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:O(N);如果退化成了单支树,那么二叉搜索树的性能就失去了。此时就需要用到即将登场的 AVL 树和红黑树了。
今天对二叉搜索树的介绍、使用、模拟实现的分享到这就结束了,希望大家读完后有很大的收获,也可以在评论区点评文章中的内容和分享自己的看法。您三连的支持就是我前进的动力,感谢大家的支持!! !
相关文章:

算法模板之单链表图文讲解
本文主要讲解单链表模板,文中附有图文讲解,希望对你的算法学习有一定的帮助。
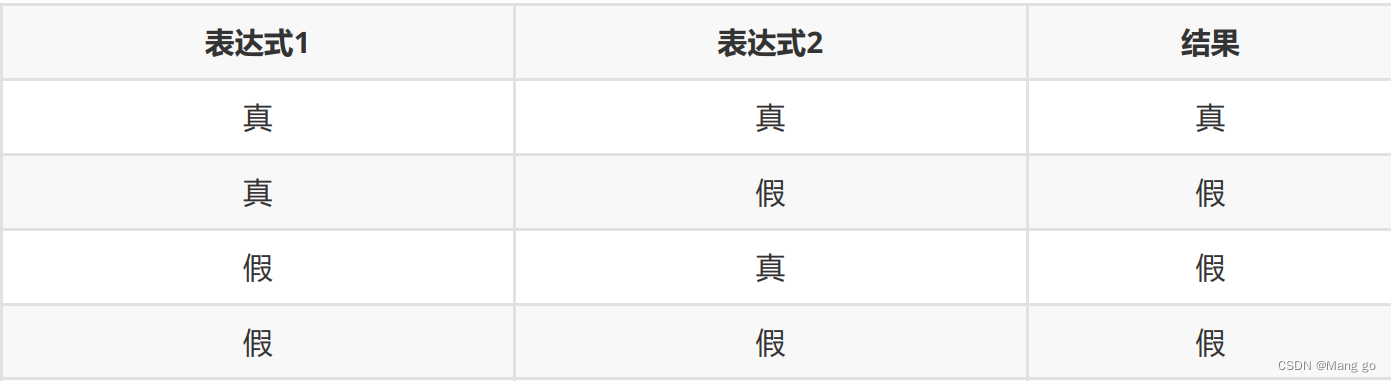
Java运算符及运算符的优先级【超详细】
int a = 10;int b = 20;a + b;a < b;对操作数进行操作时的符号,不同运算符操作的含义不同。作为一门计算机语言,Java也提供了一套丰富的运算符来操纵变量。Java中运算符可分为以下:算术运算符(+ - */)、关系运算符(< > ==)、逻辑运算符、位运算符、移位运算符以及条件运算符等,接下来我们来一个一个介绍。

Java中Jar包部署nohup后台启动定时按日期分割日志
在JAVA开发中很多没有用docker部署,而是选择传统的Jar包部署方式,这样就涉及日志的产生,如果直接部署日志文件会越来越大,程序怎么可能不出现问题,这样打开日志文件就会很慢,不方便后续问题的定位和解决。这样就要采取优化方案,对日志进行分割,这样便于查看。

Java Comparator多属性排序
自然排序通常情况跟equals保持一致,e1,e2是类C的元素,如果e1.compareTo(e2) == 0 那么e1和e2 equals的结果也是true。因为有的时候它俩结果一致,比如刚好就只有一个属性排序的时候,但多数情况下,二者是不一致的。比如有多个排序属性的时候。有的时候获取的数据需要在内存排序,需要根据List中T对象的属性p1,p2,p3等进行排序,该怎么写呢?这种规则掌握了,管它几个属性排序,管它什么升序降序,通通解决。多个属性,按不同的升降序规则,就变的非常简单了,只需要在下面的。
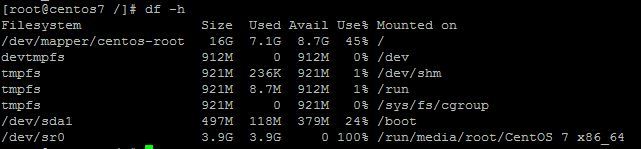
Linux 查看磁盘空间
Linux 查看磁盘空间可以使用 df 和 du 命令。
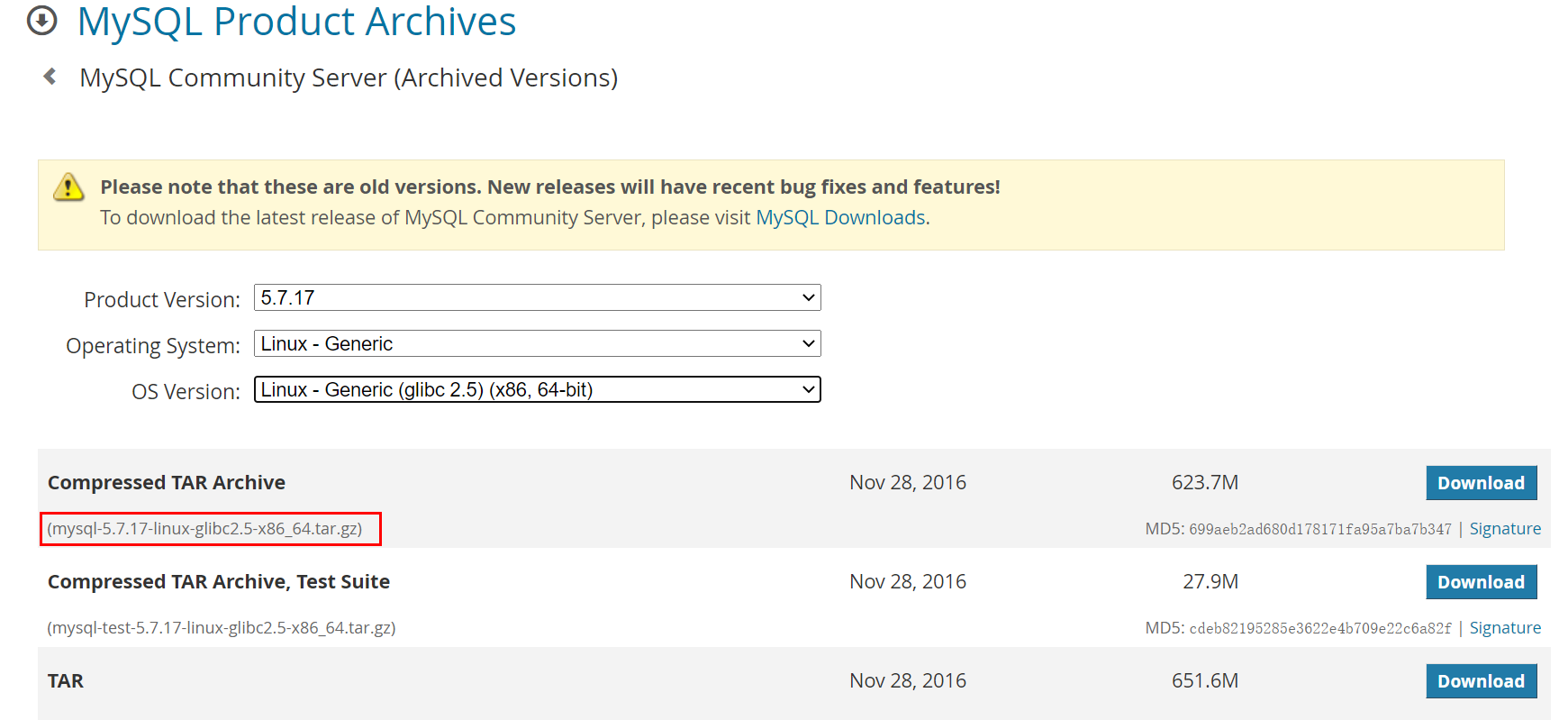
Linux多种方法安装MySQL
源码安装:优点是安装包比较小,只有十多M,缺点是安装依赖的库多,安装编译时间长,安装步骤复杂容易出错。使用官方编译好的二进制文件安装:优点是安装速度快,安装步骤简单,缺点是安装包很大,300M左右。yum安装。rpm安装。

Linux中mysql 默认安装位置&Linux 安装 MySQL
MySQL在Linux系统上的默认安装位置是目录。这是MySQL服务器的数据目录,包含所有数据库文件。通过检查MySQL二进制文件的路径,我们可以确认MySQL是否正确安装。在目录中,MySQL使用一系列文件和子目录来组织和存储数据。确保理解MySQL数据目录的结构对于管理和维护MySQL数据库至关重要。按照顺序安装即可解决。

Linux使用systemd服务和crontab实现Shell脚本开机自动运行&编辑当前用户或者指定用户的crontab内容crontab -e
systemd是Linux系统中的一个初始化系统和服务管理器。它可以用于在系统启动时自动运行Shell脚本。crontab是一个用于定时执行任务的工具。我们可以通过编辑crontab文件来设置开机自启动。
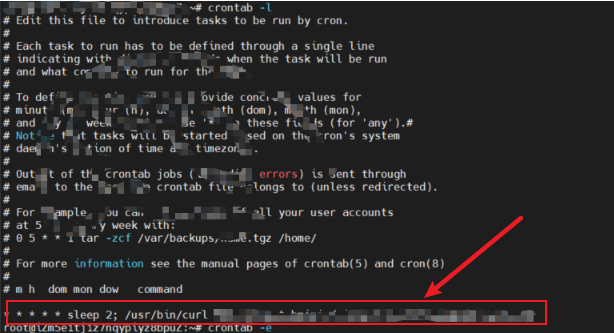
Linux定时任务详解&crontab -e 编辑之后如何保存并退出(Ubuntu)
Linux定时任务是一种可执行的命令或者脚本,在特定的时间或者时间间隔下自动执行。通过在系统中预设一些需要执行的任务,可以让Linux定时任务自动执行并完成这些任务。定时任务可以用于自动备份、系统清理、监控、自动化维护等任务。在Linux中,常用的定时任务程序有系统自带的cron和at命令。其中,cron是一个强大的定时任务工具,可以按照设定的实际时间执行命令,非常常用。anacron最小检测周期是天,使用anacron管理的定时任务应该最小是每隔一天执行。

nginx常用操作命令
都启动了同一个Nginx进程。不一样的是:1、Systemd 是一系列工具的集合,其作用也远远不仅是启动操作系统,它还接管了后台服务、结束、状态查询。2、Systemd更方便作服务管理,启动管理Nginx更佳方便。3、Systemd可以作开机服务管理,让服务跟随系统启动。

linux配置nginx开机自启&nginx部署与systemctl控制启动&/etc/systemd/system 和 /lib/systemd/system 的区别
目录/lib/systemd/system 以及/usr/lib/systemd/system 其实指向的是同一目录,在/目录下执行命令lltotal 28该目录中包含的是软件包安装的单元,也就是说通过 yum、dnf、rpm 等软件包管理命令管理的 systemd 单元文件,都放置在该目录下。/etc/systemd/system/(系统管理员安装的单元, 优先级更高)在一般的使用场景下,每一个 Unit(服务等) 都有一个配置文件,告诉 Systemd 怎么启动这个 Unit。

spring 笔记七 Spring JdbcTemplate
它是spring框架中提供的一个对象,是对原始繁琐的JdbcAPI对象的简单封装。spring框架为我们提供了很多的操作模板类。例如:操作关系型数据的JdbcTemplate和HibernateTemplate,操作nosql数据库的RedisTemplate,操作消息队列的JmsTemplate等等。
spring 笔记八 SpringMVC异常处理和SpringMVC拦截器
① 创建异常处理器类实现HandlerExceptionResolver② 配置异常处理器③ 编写异常页面④ 测试异常跳转①创建异常处理器类实现HandlerExceptionResolver@Override//处理异常的代码实现//创建ModelAndView对象②配置异常处理器③编写异常页面。

【redis】Redis 架构演化之路
里面大致说了redis的架构演进。开始学redis架构的时候,总是感觉架构好多,迷迷糊糊的,但是你知道Redis 架构演化之路之后,就明白了前因后果,这样学习更加深入以及搞笑。这篇文章我想和你聊一聊 Redis 的架构演化之路。现如今 Redis 变得越来越流行,几乎在很多项目中都要被用到,不知道你在使用 Redis 时,有没有思考过,Redis 到底是如何稳定、高性能地提供服务的?如果你对 Redis 已经有些了解,肯定也听说过。

【redis】Redis哨兵机制和集群有什么区别?
Redis哨兵机制和集群有什么区别?redis集群有几种实现方式,一个是主从集群,一个是redis cluster.

Elasticsearch分布式搜索分析引擎本地部署与远程访问
本文主要讲解如何使用Elasticsearch分布式搜索分析引擎本地部署与远程访问

讲解K-Means聚类算法进行压缩图片
在本文中,我们讲解了如何使用K-Means聚类算法来压缩图像。通过K-Means算法,我们能够找到图像中的主要颜色,并用这些颜色替换原始图像中的像素颜色,从而实现图像的压缩。这个简单的技术可以在一定程度上减小图像文件的大小,同时保持图像的可视化效果。希望这篇文章能够帮助你理解如何使用K-Means聚类算法进行图像压缩。如果你想进一步学习图像处理和压缩的知识,推荐你深入研究相关的算法和工具。

讲解pytorch可视化 resnet50特征图
然后,我们加载了查询图像,并提取了查询图像的特征。接下来,我们以类似的方式对图像数据库中的每个图像提取特征。然后,我们计算查询图像特征与数据库中每个图像特征的相似度,并根据相似度对数据库图像进行排序。通过这种方法,我们可以使用ResNet50的特征图来构建一个简单的图像检索系统。该系统可以在图像数据库中找到与查询图像相似的图像,从而在实际应用中具有广泛的用途,如图像搜索引擎、商品推荐等。这对于理解模型在图像中学到的特征非常有帮助,并帮助我们进行图像分析和理解计算机视觉模型的工作原理。最后,我们使用模型的。

讲解Unsupported gpu architecture ‘compute_*‘2017解决方法
在使用2017年以前的NVIDIA GPU进行深度学习训练时,经常会遇到"Unsupported GPU Architecture 'compute_*'"的错误。本篇文章将介绍该错误的原因并提供解决方法。

讲解c1xx: fatal error C1356: 无法找到 mspdbcore.dll
本文介绍了这个错误的原因,并提供了一些解决方案来解决这个问题。如果你遇到这个错误,请尝试上述解决方案,希望能帮助你解决这个问题并顺利进行 C++ 编程。这个错误通常出现在编译过程中,而且很可能是由于缺少或损坏了 mspdbcore.dll 文件引起的。在本文中,我们将讨论这个错误的原因,并提供一些解决方案来解决这个问题。是 Visual Studio 内部使用的一个关键文件,它提供了用于编译、链接和调试的重要功能。这有时可以清除一些隐藏的配置问题,并解决。错误时,下面的示例代码可以帮助你解决这个问题。

讲解TypeError: Class advice impossible in Python3. Use the @Implementer class decorator instead
在Python3中,当我们尝试在类上使用旧的类修饰符(class decorator)时,可能会遇到的错误。为了解决这个问题,我们可以使用类修饰符来替代旧的类修饰符。类修饰符是模块提供的一个装饰器,用于实现接口定义。通过使用类修饰符,我们可以在Python3中实现类方法和静态方法的装饰,同时保持代码的兼容性和可读性。希望本文能够帮助你理解如何解决错误,并正确使用类修饰符来装饰类方法和静态方法。

docker搭建maven私库Nexus3
阿里代理地址:http://maven.aliyun.com/nexus/content/groups/public/由于nexus的默认端口为8081,我们在启动的时候改为18091后需要修改nexus的配置文件。这样就可以在本地浏览器进入nexus页面了,地址为 服务器ip:18091。右上角登录用户名为admin,密码为之前查看的密码。配置maven-central的代理地址。删除nuget开头的仓库。同时查看admin密码。

Gitlab基础篇: Gitlab docker 安装部署、Gitlab 设置账号密码
安装docker gitlab前确保docker环境,如果没有搭建docker请查阅“Linux docker 安装文档”可以看到在docker ps -a 打印中看到 容器ID ps 展示的容器ID只时原来的一部分。修改docker镜像的gitlab容器端口前需要把gitlab容器以及docker镜像关闭。通过容器ID就能找到containers下具体哪一个是gitlab容器的配置。修改config.v2.json、hostconfig.json文件。docker 下载 gitlab容器。

spring 笔记五 SpringMVC的数据响应
上述方式手动拼接json格式字符串的方式很麻烦,开发中往往要将复杂的java对象转换成json格式的字符串,我们可以使用web阶段学习过的json转换工具jackson进行转换,导入jackson坐标。在方法上添加@ResponseBody就可以返回json格式的字符串,但是这样配置比较麻烦,配置的代码比较多,因此,我们可以使用mvc的注解驱动代替上述配置。② 将需要回写的字符串直接返回,但此时需要通过@ResponseBody注解告知SpringMVC框架,方法。

spring 笔记六 SpringMVC 获得请求数据
• SpringMVC默认已经提供了一些常用的类型转换器,例如客户端提交的字符串转换成int型进行参数设置。• 但是不是所有的数据类型都提供了转换器,没有提供的就需要自定义转换器,例如:日期类型的数据就需要自定义转换器。自定义类型转换器的开发步骤:① 定义转换器类实现Converter接口② 在配置文件中声明转换器③ 在中引用转换器①定义转换器类实现Converter接口@Overridetry {②在配置文件中声明转换器
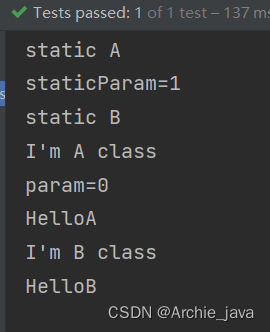
static final、static、@PostConstruct、构造方法、@AutoWired执行的顺序
Java提供的注解,被用来修饰方法,被@PostConstruct修饰的方法会在服务器加载Servlet的时候运行,并且只会被服务器执行一次。PostConstruct在构造函数之后执行,init()方法之前执行。调用的顺序为: 构造函数 > @Autowired > @PostConstruct(2)作用:@PostConstruct注解的方法在项目启动的时候执行这个方法,也可以理解为在spring容器启动的时候执行,可作为一些数据的常规化加载,比如读取数据字典之类、目录树缓存。

【HarmonyOS开发】拖拽动画的实现
在开发拖拽动画时,发现png的图片在拖拽结束后,会出现图片闪动的不流畅问题,改为svg图片解决。因此通过大量的对比验证,确认为鸿蒙底层窜然问题。

YOLOv8-Pose训练自己的数据集
至此,整个YOLOv8-Pose模型训练预测阶段完成。此过程同样可以在linux系统上进行,在数据准备过程中需要仔细,保证最后得到的数据准确,最好是用显卡进行训练。有问题评论区见!

【Redis】Redis中的大key怎么处理?
在Redis中,大key是指存储了大量数据的键。处理大key可能会对Redis服务器的性能和资源消耗产生负面影响。询问这个问题,首先要知道redis的大key会有什么影响。大key占用的内存空间较大,当大量的大key存在时,会消耗大量的内存资源。这可能导致Redis服务器的内存不足,并触发内存溢出,从而影响系统的稳定性和性能。当读取或写入大key时,需要将大量的数据通过网络传输。对于大量的网络传输,特别是在高并发的情况下,会增加整体的延迟,并占用带宽资源。

【Redis】Redis中执行Keys命令会有什么问题?
如果需要根据某种模式来获取键,更好的选择是使用更高效的命令,如SCAN命令,它使用游标方式迭代返回匹配的键,避免了遍历整个键空间的性能问题,并且可以逐步处理数据。KEYS命令用于检索匹配指定模式的所有键。如果匹配的键非常多,返回的结果列表可能巨大无比,占用大量的内存。在极端情况下,如果执行KEYS命令返回的结果集非常大,并且内存不足以容纳整个结果集,Redis服务器可能会发生内存溢出错误。如果KEYS命令运行时间较长或遇到大量匹配的键,会导致服务器长时间无法响应其他请求,从而对系统的可用性产生负面影响。

