python 累积正态分布函数_为什么机器学习都围绕正态分布进行讨论?
作者 | Farhad Malik
译者 | Monanfei
责编 | 夕颜
出品 | AI科技大本营(ID: rgznai100)
为什么正态分布如此特殊?为什么大量数据科学和机器学习的文章都围绕正态分布进行讨论?我决定写一篇文章,用一种简单易懂的方式来介绍正态分布。
在机器学习的世界中,以概率分布为核心的研究大都聚焦于正态分布。本文将阐述正态分布的概率,并解释它的应用为何如此的广泛,尤其是在数据科学和机器学习领域,它几乎无处不在。
我将会从基础概念出发,解释有关正态分布的一切,并揭示它为何如此重要。
文章结构
本文的主要内容如下:
概率分布是什么
正态分布意味着什么
正态分布的变量有哪些
如何使用 Python 来检验数据的分布
如何使用 Python 参数化生产一个正态分布
正态分布的问题
简短的背景介绍
首先,正态分布又名高斯分布
它以数学天才 Carl Friedrich Gauss 命名
正态分布又名高斯分布
越简单的模型越是常用,因为它们能够被很好的解释和理解。正态分布非常简单,这就是它是如此的常用的原因。
因此,理解正态分布非常有必要。
什么是概率分布?
首先介绍一下相关概念。
考虑一个预测模型,该模型可以是我们的数据科学研究中的一个组件。
如果我们想精确预测一个变量的值,那么我们首先要做的就是理解该变量的潜在特性。
首先我们要知道该变量的可能取值,还要知道这些值是连续的还是离散的。简单来讲,如果我们要预测一个骰子的取值,那么第一步就是明白它的取值是1 到 6(离散)。
第二步就是确定每个可能取值(事件)发生的概率。如果某个取值永远都不会出现,那么该值的概率就是 0 。
事件的概率越大,该事件越容易出现。
在实际操作中,我们可以大量重复进行某个实验,并记录该实验对应的输出变量的结果。
我们可以将这些取值分为不同的集合类,在每一类中,我们记录属于该类结果的次数。例如,我们可以投10000次骰子,每次都有6种可能的取值,我们可以将类别数设为6,然后我们就可以开始对每一类出现的次数进行计数了。
我们可以画出上述结果的曲线,该曲线就是概率分布曲线。目标变量每个取值的可能性就由其概率分布决定。
一旦我们知道了变量的概率分布,我们就可以开始估计事件出现的概率了,我们甚至可以使用一些概率公式。至此,我们就可更好的理解变量的特性了。概率分布取决于样本的一些特征,例如平均值,标准偏差,偏度和峰度。
如果将所有概率值求和,那么求和结果将会是100%
世界上存在着很多不同的概率分布,而最广泛使用的就是正态分布了。
初遇正态分布
我们可以画出正态分布的概率分布曲线,可以看到该曲线是一个钟型的曲线。如果变量的均值,模和中值相等,那么该变量就呈现正态分布。
如下图所示,为正态分布的概率分布曲线:

理解和估计变量的概率分布非常重要。
下面列出的变量的分布都比较接近正态分布:
人群的身高
成年人的血压
传播中的粒子的位置
测量误差
回归中的残差
人群的鞋码
一天中雇员回家的总耗时
教育指标
此外,生活中有大量的变量都是具有 x % 置信度的正态变量,其中,x<100。
什么是正态分布?
正态分布只依赖于数据集的两个特征:样本的均值和方差。
均值——样本所有取值的平均
方差——该指标衡量了样本总体偏离均值的程度
正态分布的这种统计特性使得问题变得异常简单,任何具有正态分布的变量,都可以进行高精度分预测。
值得注意的是,大自然中发现的变量,大多近似服从正态分布。
正态分布很容易解释,这是因为:
正态分布的均值,模和中位数是相等的。
我们只需要用均值和标准差就能解释整个分布。
正态分布是我们熟悉的正常行为
为何如此多的变量都大致服从正态分布?
这个现象可以由如下定理理解释:当在大量随机变量上重复很多次实验时,它们的分布总和将非常接近正态分布。
由于人的身高是一个随机变量,并且基于其他随机变量,例如一个人消耗的营养量,他们所处的环境,他们的遗传等等,这些变量的分布总和最终是非常接近正态的。
这就是中心极限定理。
本文的核心:
我们从上文的分析得出,正态分布是许多随机分布的总和。 如果我们绘制正态分布密度函数,那么它的曲线将具有以下特征:
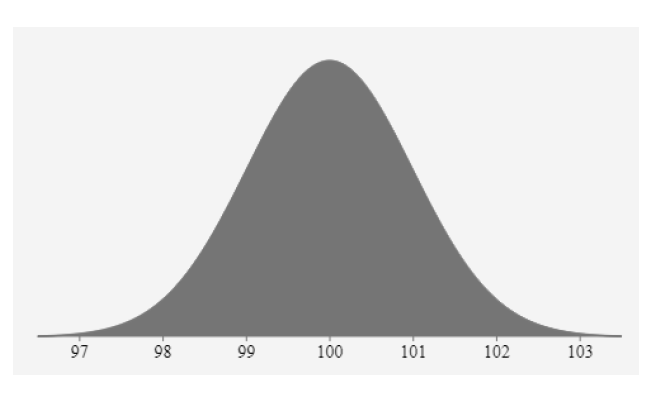
如上图所示,该钟形曲线有均值为 100,标准差为1:
均值是曲线的中心。 这是曲线的最高点,因为大多数点都是均值。
曲线两侧的点数相等。 曲线的中心具有最多的点数。
曲线下的总面积是变量所有取值的总概率。
因此总曲线面积为 100%
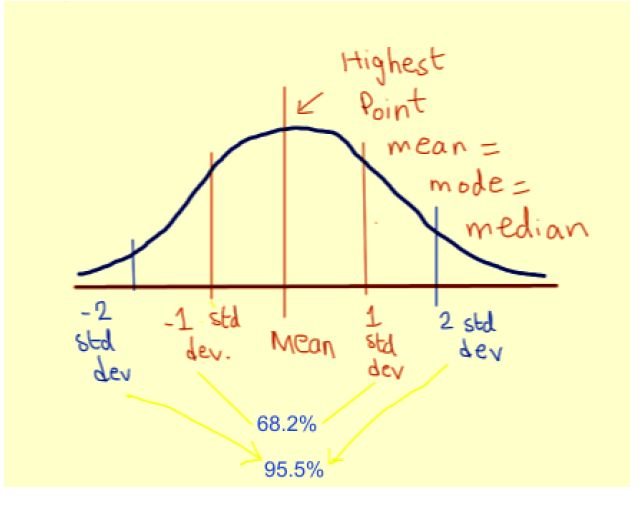
更进一步,如上图所示:
约 68.2% 的点在 -1 到 1 个标准偏差范围内。
约 95.5% 的点在 -2 到 2 个标准偏差范围内。
约 99.7% 的点在 -3 至 3 个标准偏差范围内。
这使我们可以轻松估计变量的变化性,并给出相应置信水平,它的可能取值是多少。例如,在上面的灰色钟形曲线中,变量值在 99-101 之间的可能性为 68.2%。
正态概率分布函数
概率密度函数的形式如下:

概率密度函数基本上可以看作是连续随机变量取值的概率。
正态分布是钟形曲线,其中mean = mode = median。
如果使用概率密度函数绘制变量的概率分布曲线,则给定范围的曲线下的面积,表示目标变量在该范围内取值的概率。
概率分布曲线基于概率分布函数,而概率分布函数本身是根据诸如平均值或标准差等多个参数计算的。
我们可以使用概率分布函数来查找随机变量取值范围内的值的相对概率。 例如,我们可以记录股票的每日收益,将它们分组到适当的集合类中,然后计算股票在未来获得20-40%收益的概率。
标准差越大,样品中的变化性越大。
如何使用 Python 探索变量的概率分布
最简单的方法是加载 data frame 中的所有特征,然后运行以下脚本(使用pandas 库):
DataFrame.hist(bins=10)#Make a histogram of the DataFrame.该函数向我们展示了所有变量的概率分布。
变量服从正态分布意味着什么?
如果我们将大量具有不同分布的随机变量加起来,所得到的新变量将最终具有正态分布。这就是前文所述的中心极限定理。
服从正态分布的变量总是服从正态分布。 例如,假设 A 和 B 是两个具有正态分布的变量,那么:
• A x B 是正态分布
• A + B 是正态分布
因此,使用正态分布,预测变量并在一定范围内找到它的概率会变得非常简单。
样本不服从正态分布怎么办?
我们可以将变量的分布转换为正态分布。
我们有多种方法将非正态分布转化为正态分布:
1.线性变换
一旦我们收集到变量的样本数据,我们就可以对样本进行线性变化,并计算Z得分:
计算平均值
计算标准偏差
对于每个 x,使用以下方法计算 Z:

2.使用 Boxcox 变换
我们可以使用 SciPy 包将数据转换为正态分布:
scipy.stats.boxcox(x, lmbda=None, alpha=None)3.使用 Yeo-Johnson 变换
另外,我们可以使用 yeo-johnson 变换。 Python 的 sci-kit learn 库提供了相应的功能:
sklearn.preprocessing.PowerTransformer(method=’yeojohnson’,standardize=True, copy=True)正态分布的问题
由于正态分布简单且易于理解,因此它也在预测研究中被过度使用。 假设变量服从正态分布会有一些显而易见的缺陷。 例如,我们不能假设股票价格服从正态分布,因为价格不能为负。 因此,我们可以假设股票价格服从对数正态分布,以确保它永远不会低于零。
我们知道股票收益可能是负数,因此收益可以假设服从正态分布。
假设变量服从正态分布而不进行任何分析是愚蠢的。
变量可以服从Poisson,Student-t 或 Binomial 分布,盲目地假设变量服从正态分布可能导致不准确的结果。
总结
本文阐述了正态分布的概念和性质,以及它如此重要的原因。
希望能帮助到你。
原文链接:http://bit.ly/2NyetFz
(*本文为 AI科技大本营翻译文章,转载请联系 1092722531)
相关文章:

Silverlight开发中遇到的几个小问题
1,程序发布时遇到错误: "Could not load type System.ServiceModel.Activation.HttpModule from assembly System.ServiceModel, Version3.0.0.0, Cultureneutral, PublicKeyTokenb77a5c561934e089" 可能引发此问题的原因: 安装.N…

最新DynamipsGUI2.8[模拟器]发布!(中文版-英文版下载)
DynamipsGUI2.8发布!2.0beta新增功能1.支持分布式Dynamips,最多支持9台PC联合进行路由交换模拟(可能存在问题,请测试提出问题)2.设备支持数量增加至路由器44台,交换机44台,适应超大型环境模拟3.支持2691,3725,3745(可能存在问题,请测试提出问题)4.集成最新dynamips-…

ue4 函数和宏区别_【UE4】通俗易懂 用蓝图来学习 C++ 基础知识
【前言】:用老罗来学UE蓝图:https://zhuanlan.zhihu.com/p/135297007zhuanlan.zhihu.com再开个脑洞,用蓝图来类比学习C基础知识。C 刚开始学,所以本篇知识点不是特别全有些地方也可能不是特别准,望谅解,以…

c#自动登录网页,浏览页面
需求:客户的数据同时存在在另外一个不可控的系统中,需要和当前系统同步。 思路:自动登录另外一个系统,然后抓取数据,同步到本系统中。 技术点:模拟用户登录;保存登录状态;抓取数据 程…
用Servlet获取表单数据
1 //accept.jsp2 package servlets;3 4 import java.io.*;5 import javax.servlet.*;6 import javax.servlet.http.*;7 public class accept extends HttpServlet8 { 9 public String codeToString(String str) 10 {//处理中文字符串的函数 11 String sstr; 12 …

品质检测破局:工业视觉检测云平台为智能制造“点睛”
微波炉角落里的型号编码、空调背面不显眼的小螺钉、冰箱侧身的标签,它们的质量检测是生产线中最费人工的地方,也是制约智能制造的老大难。如果哪天这类瑕疵检测不再需要人工,这样的制造就真的称得上智能。最近,这一难题被美的和英…

算法导论Java实现-构建MaxHeap
package lhz.algorithm.chapter.six; /** * “构建堆”,《算法导论》6.3章节 Building a heap * 利用之前实现的<code>MaxHeapify</code>算法,构建max-heap。 * 伪代码: * BUILD-MAX-HEAP(A) * 1 heap-size[A] ← length[A]…
哲学家就餐问题c语言_哲学家就餐问题的一种Python解决方案
哲学家就餐问题一直是多线程同步问题的经典案例,本文中展示了多线程竞争共享资源带来的死锁问题,并介绍了一种简单的解决方案。哲学家就餐问题哲学家最擅长的就是思考和吃饭 ,当他们感觉累的时候,就会拿起一双筷子去吃盘子里的寿司…

倒计时1天,2018 AI开发者报名通道即将关闭(附参会提醒)
参加 2018 AI开发者大会,请点击 ↑↑↑随着 AI 逐渐转为各大科技巨头的战略主战场,人工智能技术亦是长立风口,向阳而生。越来越多的发展趋势表明,未来的人工智能将逐步迈入广泛普及阶段,继而深入影响人类日常的生产生活…

Linux安全检查方法
检查系统密码文件,查看文件修改日期 [rootfedora ~]# ls -l /etc/passwd 查看passwd文件中有哪些特权用户 [rootfedora ~]# awk -F: $30 {print $1} /etc/passwd 查看系统里有没有空口令帐户 awk -F: length($2)0 {print $1} /etc/shadow 检查系…

Ubuntu Server 12.04下cobbler + dnsmasq +tftpd-hpa的安装配置(四)
四、自定义 kickstart 文件 Kickstart最早是RedHat公司用来自动部署RedHat操作系统的,通过Kickstart配置文件,通常安装过程中需要交互输入的信息就都可以自动应答。 通过Kickstart安装操作系统一般是这样几个步骤: Create a kickstart file. …
AI 技术实力图谱全解析!2018 中国 AI 开发者大会重磅来袭
【2018 AI 开发者大会图文直播】 11 月 8 日,由中国专业 IT 社区 CSDN 与硅谷 AI 社区 AICamp 联合出品的 2018 中国 AI 开发者大会(AI NEXTCon) 在北京拉开帷幕,近百位中美顶尖 AI 专家、知名企业代表、逾千名 AI 开发者&#x…

sql的不等于条件优化_SQL优化案例(2):OR条件优化
随后上一篇文章《 SQL优化案例(1):隐式转换》的介绍,此处内容围绕OR的优化展开。在MySQL中,同样的查询条件,如果变换OR在SQL语句中的位置,那么查询的结果也会有差异,在多个复杂的情况下,可能会带…

所有 SAP 现在开设的标准课程
下面是 SAP 中国的教育培训首页,里面有 SAP 最新最完整的培训教育计划。 http://www30.sap.com/china/services/education/index.epx 从中可以看出,随着 SAP 的发展,BC4xx 系列课程已经发生了很大改变,取消了 BC404、BC406&#x…
动态展开所有_库存与市场需求之间如何“动态”共舞?库存计划动态模型构建分享...
库存(Stock)是用来提高交货速度、缓冲需求到单高峰的常用手段,通过按库存生产(MTS)的方法,用储备库存来满足客户需求、并按一定规则补货,无需等待生产周期,可极快地交付。相比按订单生产(MTO)的模式,采用安全库存可以有…

Linux下DNS简单部署(主从域名服务器)
一、DNS简介 DNS(Domain Name System),域名系统,因特网上作为域名和IP地址相互映射的一个分布式数据库,能够使用户更方便的访问互联网,而不用去记住能够被机器直接读取的IP数串。通过主机名,最终…

Neurala与CSDN宣布战略合作,将一站式AI平台BrainBuilder带给中国开发者
11 月 8 日,美国人工智能创新企业 Neurala 与中国开发者社区 CSDN 联合宣布,正式成为战略合作伙伴,通过双方的合作,将 BrainBuilder 平台提供给中国的更多开发者和教育培训机构。Brain Builder 是 Neurala 开发的一站式 AI 平台。…

使用idea创建springboot项目并打成war包发布到weblogic上...
部署tomcat也是类似的,但是需要注意项目配置的路径,或者直接将项目放到webapp的ROOT目录下。 使用工具:intelliJ IDEA2016.3, jdk1.8 ,weblogic12 一 使用idea创建springboot项目 File-》New -》Project 选择jdk版本…

cs架构嵌入bs_CS与BS架构区别、比较、及现状与趋势分析
一、简介 CS即Client/Server(客户机/服务器)结构,C/S结构在技术上很成熟,它的主要特点是交互性强、具有安全的存取模式、网络通信量低、响应速度快、利于处理大量数据。但是该结构的程序是针对性开发,变更不够灵活,维护和管理的难…

大数据的“平民化”、“流动化”、“商业化”推动企业升级与转型
CSDN 出品的《2018-2019 中国人工智能产业路线图》V2.0 版已经重磅面世! V1.0 版发布以来,我们有幸得到了诸多读者朋友及行业专家的鼎力支持,在此表示由衷感谢。此次 V2.0 版路线图进行了新一轮大升级,内容包括 3 大 AI 前沿产业趋…

APIPA是什么?
<?xml:namespace prefix o ns "urn:schemas-microsoft-com:office:office" />APIPA(Automatic Private IP Addressing,自动专用IP寻址自动专用IP寻址),是一个DHCP故障转移机制。当DHCP服务器出故障时ÿ…

birt报表表格边框_手把手教你五步制作出一张领导驾驶舱报表
领导驾驶舱报表是一款为企业内部领导及相关高管提供企业数据指标分析的报表,用来实时反映企业的运行状况,将企业管理决策提升到一个新的高度。今天小编用亿信华辰的亿信ABI给大家实际演示,通过5个步骤就可以刷刷刷“变”出漂亮的领导驾驶舱&a…

Web的现状:网页性能提升指南
互联网发展非常迅速,所以我们创造了Web平台。通常 我们会忽视连通性等问题,但用户们却不会视而不见 。一瞥万维网的现状,可以发现我们并没有用同情心、变通意识去构建它,更不要说性能了。 所以,今天的Web是什么状态呢?…

[导入]ExtJs 2.0 弹窗事例
网站: JavaEye 作者: ppkosd 链接:http://ppkosd.javaeye.com/blog/133004 发表时间: 2007年10月18日 责任不是你应该做的事情,而是你必须做的事情 -- ppkosd 这个EXT 2.0 的例子 讲的是怎么样用aspserver和ext2.0构建弹窗效果! 服务器部分: 代码va…

双十一报名截止,决赛在即!AI Challenger2018极客峰会免费抢票!
第二届“AI Challenger 全球AI挑战赛”各赛道竞赛经过两个多月的激烈角逐,报名将于北京时间2018年11月11日23:59:59正式截止,随即进入决赛阶段,最终每个竞赛的TOP 5团队将进入12月18、19日在北京举办的总决赛答辩及颁奖礼,角逐超过…

取值范围_从int取值范围谈起
int取值范围我们在面试过程中,或者在准备面试过程中,可能会遇到这样一个问题:Java中int的取值范围是什么?这个问题比较常见,也很简单,相信大部分Java开发人员都可以快速答上来:[ , ]即使不能马上…

MonoRail学习笔记五:定制服务实现自定义功能
在上一篇MonoRail学习笔记四:MonoRail基本流程分析中我提到,MonoRail中可以自定义一些服务。比如可以定义自己的Url解析类,来实现http://localhost:***/index.rails等http://localhost:***/*.rails的效果。具体步骤如下:1、修改we…

我的第一个vb实例--红楼梦测试小程序
http://files.cnblogs.com/gengxiaochao/hlmtest.rar 转载于:https://www.cnblogs.com/gengxiaochao/archive/2007/11/26/973072.html

2018 AI产业投融资分析:热钱涌向何处,谁的“寒冬”将至?
AI科技大本营按:本篇内容来自由 CSDN 出品的《2018 中国人工智能产业路线图》V2.0 版中 1.4 章投融资分析篇,通过对各大 AI 行业进行相关数据分析,我们尽可能勾勒出中国 AI 产业发展现状,并对行业未来做出趋势判断。产业路线图 2.…
mvc的宿舍管理系统源码 基于jsp_[源码和文档分享]基于JSP的MVC框架实现的图书推荐系统展示平台网站...
推荐系统是目前互联网中最常见的一种智能产品形式。由于网络中信息量的快速增长以及图书出版行业出版量的攀升,人们需要一种办法,来解决信息过载的问题。此外,用户访问网络是为了获取信息,但并不是所有的访问都有很强的目的性&…
