当前位置：首页 > 编程日记 > 正文

行列式介绍及Eigen/OpenCV/C++的三种实现

编程日记 2024-12-22 17:40:00

行列式，记作det(A)，是一个将方阵A映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是0，那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是1，那么这个转换保持空间体积不变。

行列式(Determinant)是数学中的一个函数，将一个n*n的矩阵A映射到一个标量，记作det(A)或|A|。行列式可以看作是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说，在n维欧几里得空间中，行列式描述的是一个线性变换对”体积”所造成的影响。

对于简单的2阶和3阶的矩阵，行列式的表达式相对简单，而且恰好是每条主对角线(左上至右下)元素乘积之和减去每条副对角线(右上至左下)元素乘积之和。

一个n阶方块矩阵A的行列式可直观地定义如下，来自于维基百科：

按照拉普拉斯公式进行递推计算：

对一个n阶的行列式M，去掉M的第i行第j列后形成的n-1阶的行列式叫做M关于元素m_ij的余因式(又称余子式)，记作M_ij。

M关于元素m_ij的代数余子式记作C_ij：C_ij=(-1)^(i+j)*M_ij。

一个n阶的行列式M可以写成一行(或一列)的元素与对应的代数余子式的乘积之和，叫做行列式按一行(或一列)的展开，如：

det(A)=a₁₁C₁₁+a₂₁C₂₁+…+a_n1C_n1或 det(A)=a₁₁C₁₁+a₁₂C₁₂+…+a_1nC_1n

这个公式又称拉普拉斯公式，把n维矩阵的行列式计算变成了n个n-1维的行列式的计算。另一方面，拉普拉斯公式可以作为行列式的一种归纳定义。

行列式性质：

(1)、单位矩阵的行列式为1，若矩阵的某几行线性相关，则它的行列式为零。

(2)、一个矩阵的行列式等于它的转置矩阵的行列式。

(3)、在行列式中，一行(列)元素全为0，则此行列式的值为0。

(4)、在行列式中，某一行(列)有公因子k，则可以提出k。

(5)、在行列式中，某一行(列)的每个元素是两数之和，则此行列式可拆分为两个相加的行列式。

(6)、行列式中的两行(列)互换，改变行列式正负符号。

(7)、在行列式中，有两行(列)对应成比例或相同，则此行列式的值为0。

(8)、将一行(列)的k倍加进另一行(列)里，行列式的值不变。注：一行(列)的k倍加上另一行(列)，行列式的值改变。

(9)、将行列式的行列互换，行列式的值不变，其中行列互换相当于转置。这个性质可以简单地记作：D=|a_ij|=|a_ji|=D^T

(10)、行列式的乘法定理：方块矩阵的乘积的行列式等于行列式的乘积：det(AB) = det(A)det(B)

(11)、若A是可逆矩阵，det(A^-1)=(det(A))^-1

(12)、若两个矩阵相似，那么它们的行列式相同。

(13)、行列式是所有特征值(按代数重数计)的乘积。

行列式的计算：(1)、按照定义公式；(2)、按照拉普拉斯公式进行递归计算；(3)、利用高斯消去法；(4)、LU分解法。

以下测试代码是采用Eigen实现的行列式计算：

int test_mat_determinant()
{std::vector<float> vec{ 1, 0, 2, -1, 3, 0, 0, 5, 2, 1, 4, -3, 1, 0, 5, 0 };Eigen::Map<Eigen::Matrix<float, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> map(vec.data(), 4, 4);double det = map.determinant();fprintf(stderr, "det: %f\n", det);return 0;
}

执行结果如下：

以下是分别采用OpenCV和C++实现的行列式计算：

#include "funset.hpp"
#include <math.h>
#include <iostream>
#include <string>
#include <vector>
#include <opencv2/opencv.hpp>static double determinant_opencv(const std::vector<float>& vec)
{int length = std::sqrt(vec.size());cv::Mat mat(length, length, CV_32FC1, const_cast<float*>(vec.data()));// In OpenCV, for small matrices(rows=cols<=3),the direct method is used.// For larger matrices the function uses LU factorization with partial pivoting.return cv::determinant(mat);
}template<typename _Tp>
static _Tp det(const std::vector<std::vector<_Tp>>& mat, int N)
{if (mat.size() != N) {fprintf(stderr, "mat must be square matrix\n");return -1;}for (int i = 0; i < mat.size(); ++i) {if (mat[i].size() != N) {fprintf(stderr, "mat must be square matrix\n");return -1;}}_Tp ret{ 0 };if (N == 1) return mat[0][0];if (N == 2) {return (mat[0][0] * mat[1][1] - mat[0][1] * mat[1][0]);} else {// first colfor (int i = 0; i < N; ++i) {std::vector<std::vector<_Tp>> m(N - 1);std::vector<int> m_rows;for (int t = 0; t < N; ++t) {if (i != t) m_rows.push_back(t);}for (int x = 0; x < N - 1; ++x) {m[x].resize(N - 1);for (int y = 0; y < N - 1; ++y) {m[x][y] = mat[m_rows[x]][y + 1];}}int sign = (int)pow(-1, 1 + i + 1);ret += mat[i][0] * sign * det<_Tp>(m, N-1);}}return ret;
}int test_determinant()
{std::vector<float> vec{ 1, 0, 2, -1, 3, 0, 0, 5, 2, 1, 4, -3, 1, 0, 5, 0};const int N{ 4 };if (vec.size() != (int)pow(N, 2)) {fprintf(stderr, "vec must be N^2\n");return -1;}double det1 = determinant_opencv(vec);std::vector<std::vector<float>> arr(N);for (int i = 0; i < N; ++i) {arr[i].resize(N);for (int j = 0; j < N; ++j) {arr[i][j] = vec[i * N + j];}}double det2 = det<float>(arr, N);fprintf(stderr, "det1: %f, det2: %f\n", det1, det2);return 0;
}

执行结果如下：

经测试，使用C++实现的行列式的计算与调用OpenCV和Eigen接口实现的结果是一致的。

GitHub：

https://github.com/fengbingchun/NN_Test

https://github.com/fengbingchun/Eigen_Test

https://www.dkcj.cn/info/32970.html

行列式介绍及Eigen/OpenCV/C++的三种实现

相关文章：

基于Go的语义解析开源库FMR，“屠榜”模型外的NLP利器

【高级数据类型2】- 10. 接口

Linux软件包命令

Caffe中计算图像均值的实现(cifar10)

阿里云弹性公网IP（EIP）的使用限制

400名微软员工主动曝光薪资：28万元到228万元不等！

Extjs:添加查看全部按钮

练手扎实基本功必备：非结构文本特征提取方法

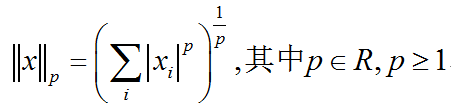
范数介绍及C++/OpenCV/Eigen的三种实现

js添加网页水印和three.js场景中加水印

JAVA学习笔记（6）

C++/C++11中std::deque的使用

贾扬清：我对人工智能方向的一点浅见

吴甘沙：天外飞“厕”、红绿灯消失，未来无人驾驶将被重新定义

Linux内核--网络栈实现分析（二）--数据包的传递过程--转

C++/C++11中std::stack的使用

团队前四次作业——个人总结

吴甘沙：天外飞“厕”、红绿灯消失，未来无人驾驶将被重新定义 | AI ProCon 2019

MySQL基础day03_数据的导入、导出-MySQL 5.6

“含光”剑出，谁与争锋？阿里重磅发布首颗AI芯片含光800

c++面试题中经常被面试官面试的小问题总结（一）（本篇偏向基础知识）

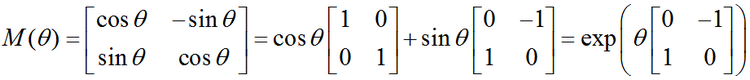
矩阵特征分解介绍及雅克比(Jacobi)方法实现特征值和特征向量的求解(C++/OpenCV/Eigen)

Entity Framework CodeFirst数据迁移

限时早鸟票 | 2019 中国大数据技术大会（BDTC）超豪华盛宴抢先看！

Google AI 系统 DeepMind无法通过高中数学

C++11中std::tuple的使用

PHP Countable接口

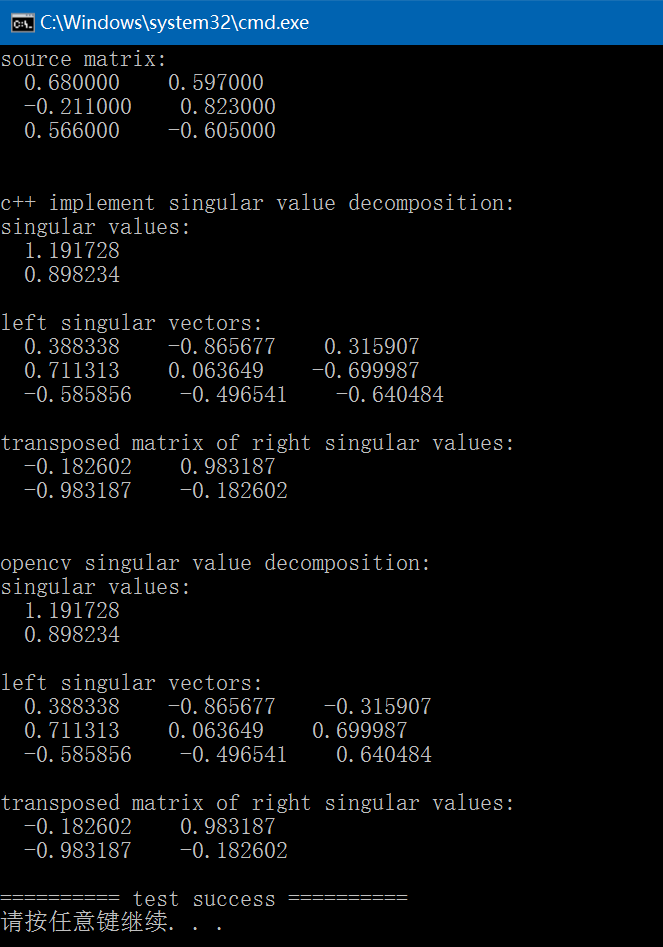
矩阵奇异值分解简介及C++/OpenCV/Eigen的三种实现

经典！工业界深度推荐系统与CTR预估必读的论文汇总

docker上传自己的镜像