当前位置：首页 > 编程日记 > 正文

昨天，我用 Python 写了一个婚介模型

编程日记 2024-11-24 03:20:00

作者 | 天元浪子
来源 | CSDN（ID：CSDNnews）

先声明一下：本文纯属七夕应景娱乐之作。如果有人因为遵循本模型提出的择偶理论而导致失恋或单身，除了同情，我不能补偿更多。

在中国的传统节日里，七夕可能是起源最神秘、内涵最深刻的一个了。当然，这不是本文的重点，我们的核心问题是：在七夕这个特有纪念意义的日子，你真的想好了要向TA表白吗？TA 真的是你唯一正确的选择吗？这个婚介模型，也许对你有一些启发。

我的婚介所生意兴隆，无数想找到理想伴侣的单身人士都来光顾。根据颜值、人品、能力、财富等因素，我给每位客户确定了一个素质指数（Quality Index），简写为 qidx。统计发现，qidx 呈现均值 8.0、标准差 0.5 正态分布。

下面是1万客户的 qidx 统计分布图，可以看出绝大多数单身人士的 qidx 位于 7.0~9.0 之间，评价较为负面的和非常优秀的，都属于少数派。

import numpy as np
import matplotlib.pyplot as pltsingles = np.random.normal(loc=8.0, scale=0.5, size=10000)
plt.hist(singles, bins=8, histtype='step')
plt.show()

一般情况下，我的客户缴费 1 次，将获得有 10 次选择机会。我向客户推荐目标的策略基于“门当户对”，总是选择和客户的 qidx 相适应的异性，具体说就是以客户的 qidx 为均值，以 0.1 的方差，按照正态分布随机生成。

通常，客户有两种方式从我为他们推荐的目标中做出选择。第一种是基于传统的择偶观念，具体规则如下：

有 10% 的客户会对当前的推荐目标一见钟情，不在意双方的 qid 是否匹配。
如果当前推荐目标的 qid 比客户高，但不超过 0.2，客户选择当前推荐目标的概率，会随剩余选择机会的减少而增加，大约从 0.35 升至 0.8。
如果当前推荐目标的 qid 比客户高 0.2 以上，客户选择当前推荐目标的概率，会随剩余选择机会的减少而增加，大约从 0.55 升至 1.0。
如果当前推荐目标的 qid 比客户低，但不超过 0.2，客户选择当前推荐目标的概率，会随剩余选择机会的减少而增加，大约从 0.25 升至 0.7。
如果当前推荐目标的 qid 比客户低 0.2 以上，求偶者选择当前目标的概率，会随剩余选择机会的减少而增加，大约从 0 升至 0.18。

第二种匹配方式则是基于“麦穗理论”，听起来很高大上。这里省略了关于麦穗理论的讲解，感兴趣的同学可以自行检索。具体说，就是客户在前 4 次的推荐中，不做出选择，只记下其中的最高的 qidx；从第 5 次开始，只要遇到大于或等于前 4 次最高 qidx 的推荐目标，就做出选择。

下面，我分别用两种匹配方式为 1 万名顾客选择配偶，结果会怎样呢？

# -*- encoding: utf-8 -*-import numpy as npclass Single:def __init__(self, qidx, times):self.times = times # 婚介所提供的匹配次数self.counter = 0 # 当前匹配次数self.qidx = qidx # 客户的qidxself.spouse = None # 匹配成功的配偶的qidxself.histroy = list() # 基于麦穗理论的前times/e次的推荐对象的qidxdef math_classical(self, spouse):self.counter += 1if np.random.random() < 0.1:self.spouse = spouseif spouse - self.qidx >= 0.2:if np.random.random() < 1-0.05*(10-self.counter):self.spouse = spouseelif spouse - self.qidx > 0:if np.random.random() < 0.8-0.05*(10-self.counter):self.spouse = spouseelif self.qidx - spouse >= 0.2:if np.random.random() < 0.18-0.02*(10-self.counter):self.spouse = spouseelif self.qidx - spouse >= 0:if np.random.random() < 0.7-0.05*(10-self.counter):self.spouse = spousedef match_technical(self, spouse):self.counter += 1if self.counter < self.times/np.e:self.histroy.append(spouse)elif spouse >= max(self.histroy):self.spouse = spousedef main(math_mode, total=10000, times=10):# 生成总数为total的客户，其qids有正态随机函数生成singles = [Single(np.random.normal(loc=8.0, scale=0.5), times) for i in range(total)]for p in singles:for i in range(10):if p.counter < 10 and not p.spouse:spouse = np.random.normal(loc=p.qidx, scale=0.1)getattr(p, math_mode)(spouse)matched = np.array([(p.qidx, p.spouse) for p in singles if p.spouse])diff = matched[:,0] - matched[:,1]print('----------------------------------')print('成功匹配%d人，成功率%0.2f%%'%(matched.shape[0], matched.shape[0]*100/total))print('客户qidx均值%0.2f，配偶均值%0.2f'%(np.sum(matched[:,0])/matched.shape[0], np.sum(matched[:,1])/matched.shape[0]))print('匹配方差%0.2f，匹配标准差%0.2f'%(diff.var(), diff.std()))print()if __name__ == '__main__':print('基于传统方式择偶的统计结果')main('math_classical')print('基于麦穗理论择偶的统计结果')main('match_technical')

比较两种方案的匹配成功率、匹配成功的客户的平均 qids、匹配成功的客户配偶的平均 qids、客户和配偶的 qids 的方差等，你会发现，这个结果真的有点意思。

基于传统方式择偶的统计结果
----------------------------------
成功匹配10000人，成功率100.00%
客户qidx均值8.00，配偶均值8.02
匹配方差0.01，匹配标准差0.10基于麦穗理论择偶的统计结果
----------------------------------
成功匹配7138人，成功率71.38%
客户qidx均值8.00，配偶均值8.11
匹配方差0.00，匹配标准差0.07

结论：

基于传统方式的择偶，成功率更高（100% VS 71.38%）；
基于麦穗理论择偶，配偶素质指数更高（8.11 VS 8.02）；
基于麦穗理论择偶，双方qids差的标准差更小（0.07 VS 0.10），这意味着双方匹配更好。

声明：本文为 CSDN 博主「天元浪子」的原创稿件，版权归作者所有。
原文地址：https://blog.csdn.net/xufive/article/details/108214016

更多精彩推荐

鸿蒙加海思，麒麟加龙芯，组合拳能否渡劫“生态”危机
用 Python 详解《英雄联盟》游戏取胜的重要因素！
万字长文总结机器学习的模型评估与调参 | 附代码下载
“Talk is cheap, show me the code”你一行代码有多少漏洞？
科普 | 定义 Eth2.0 中的验证者质量

https://www.dkcj.cn/info/28854.html

昨天，我用 Python 写了一个婚介模型

相关文章：

WCF服务一：WCF服务简介

MIT 更新最大自然灾害图像数据集，囊括 19 种灾害事件

DataBind数据核心

convertViewsetTag方法的一点理解

iOS使用Security.framework进行RSA 加密解密签名和验证签名

Android APK反编译详解（附图）

你不知道的18个Python高效编程技巧

Alisql源码编译安装(详细篇)

如何给DataGrid添加自动增长列

达摩院NLP团队斩获六项世界冠军背后，让AI没有难懂的语言

提权巧用RAR.EXE

OSGI企业应用开发（二）Eclipse中搭建Felix运行环境

马斯克脑机接口、BrainOS相继发布，不努力也能有出路了

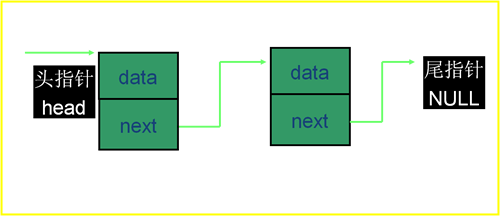
C语言单向链表的实现

Java开发常用Linux命令

数据库开发基本操作-安装Sql Server 2005出现“性能监视器计数器要求”错误解决方法...

华为昇腾师资培训沙龙·南京场 |华为昇腾 ACL 语言开发实践全程干货来了！看完就实操系列...

设计模式之C#实现---Builder

微信小程序开发之不能使用eval函数的问题

设计模式之C#实现--FactoryMethod

美国AI博士指出，自学Python到底能做什么

关于微博溯源的后续问题

python3的数据类型以及模块的含义

设计模式之C#实现---- ProtoType

快速排序（二）最后修改

性能超越GPU、FPGA，华人学者提出软件算法架构加速AI实时化

PHP获取毫秒时间戳，利用microtime()函数

.NET中添加控件数组

如何在机器学习的框架里实现隐私保护？

函数图像轻松画：教你用永中图象