R语言通过loess去除某个变量对数据的影响

当我们想研究不同sample的某个变量A之间的差异时，往往会因为其它一些变量B对该变量的固有影响，而影响不同sample变量A的比较，这个时候需要对sample变量A进行标准化之后才能进行比较。标准化的方法是对sample 的 A变量和B变量进行loess回归，拟合变量A关于变量B的函数 f(b)，f(b)则表示在B的影响下A的理论取值，A-f(B)（A对f(b）残差）就可以去掉B变量对A变量的影响,此时残差值就可以作为标准化的A值在不同sample之间进行比较。

Loess局部加权多项式回归

LOWESS最初由Cleveland 提出,后又被Cleveland&Devlin及其他许多人发展。在R中loess 函数是以lowess函数为基础的更复杂功能更强大的函数。主要思想为:在数据集合的每一点用低维多项式拟合数据点的一个子集,并估计该点附近自变量数据点所对应的因变量值,该多项式是用加权最小二乘法来拟合;离该点越远,权重越小,该点的回归函数值就是这个局部多项式来得到,而用于加权最小二乘回归的数据子集是由最近邻方法确定。
  最大优点:不需要事先设定一个函数来对所有数据拟合一个模型。并且可以对同一数据进行多次不同的拟合，先对某个变量进行拟合，再对另一变量进行拟合，以探索数据中可能存在的某种关系，这是普通的回归拟合无法做到的。

LOESS平滑方法

1. 以x₀为中心确定一个区间，区间的宽度可以灵活掌握。具体来说，区间的宽度取决于q=fn。其中q是参与局部回归观察值的个数，f是参加局部回归观察值的个数占观察值个数的比例,n是观察值的个数。在实际应用中，往往先选定f值，再根据f和n确定q的取值，一般情况下f的取值在1/3到2/3之间。q与f的取值一般没有确定的准则。增大q值或f值，会导致平滑值平滑程度增加，对于数据中前在的细微变化模式则分辨率低，但噪声小，而对数据中大的变化模式的表现则比较好；小的q值或f值，曲线粗糙，分辨率高，但噪声大。没有一个标准的f值，比较明智的做法是不断的调试比较。
  2. 定义区间内所有点的权数，权数由权数函数来确定，比如立方加权函数weight = (1 - (dist/maxdist)^3)^3),dist为距离x的距离，maxdist为区间内距离x的最大距离。任一点(x₀,y₀)的权数是权数函数曲线的高度。权数函数应包括以下三个方面特性：(1)加权函数上的点(x₀,y₀)具有最大权数。(2)当x离开x₀₍时，权数逐渐减少。(3)加权函数以x₀为中心对称。
  3. 对区间内的散点拟合一条曲线y=f(x)。拟合的直线反映直线关系，接近x₀的点在直线的拟合中起到主要的作用，区间外的点它们的权数为零。
  4. x₀的平滑点就是x₀在拟合出来的直线上的拟合点(y₀,f( x₀))。
  5. 对所有的点求出平滑点，将平滑点连接就得到Loess回归曲线。

R语言代码

 loess(formula, data, weights, subset, na.action, model = FALSE,span = 0.75, enp.target, degree = 2,parametric = FALSE, drop.square = FALSE, normalize = TRUE,family = c("gaussian", "symmetric"),method = c("loess", "model.frame"),control = loess.control(...), ...)

formula是公式，比如y~x,可以输入1到4个变量;
  data是放着变量的数据框，如果data为空，则在环境中寻找;
  na.action指定对NA数据的处理，默认是getOption("na.action");
  model是否返回模型框；
  span是alpha参数，可以控制平滑度,相当于上面所述的f，对于alpha小于1的时候，区间包含alpha的点，加权函数为立方加权，大于1时，使用所有的点，最大距离为alpha^(1/p)，p 为解释变量;
  anp.target，定义span的备选方法；
  normalize，对多变量normalize到同一scale；
  family，如果是gaussian则使用最小二乘法，如果是symmetric则使用双权函数进行再下降的M估计；
  method，是适应模型或者仅仅提取模型框架；
  control进一步更高级的控制，使用loess.control的参数；
  其它参数请自己参见manual并且查找资料

loess.control(surface = c("interpolate", "direct"),statistics = c("approximate", "exact"),trace.hat = c("exact", "approximate"),cell = 0.2, iterations = 4, ...)

surface，拟合表面是从kd数进行插值还是进行精确计算；
  statistics,统计数据是精确计算还是近似，精确计算很慢
  trace.hat,要跟踪的平滑的矩阵精确计算或近似？建议使用超过1000个数据点逼近，
  cell,如果通过kd树最大的点进行插值的近似。大于cell floor(nspancell)的点被细分。
  robust fitting使用的迭代次数。

predict(object, newdata = NULL, se = FALSE,na.action = na.pass, ...)

object，使用loess拟合出来的对象；
  newdata,可选数据框，在里面寻找变量并进行预测；
  se,是否计算标准误差；
  对NA值的处理

实例

生物数据分析中，我们想查看PCR扩增出来的扩增子的测序深度之间的差异，但不同的扩增子的扩增效率受到GC含量的影响，因此我们首先应该排除掉GC含量对扩增子深度的影响。

数据

amplicon 测序数据，处理后得到的每个amplicon的深度，每个amplicon的GC含量，每个amplicon的长度

先用loess进行曲线的拟合

gcCount.loess <- loess(log(RC+0.01)~GC,data=RC_DT,control = loess.control(surface = "direct"),degree=2)

画出拟合出来的曲线

predictions1<- predict (gcCount.loess,RC_DT$GC)
#plot scatter and line 
plot(RC_DT$GC,log(RC_DT$RC+0.01),cex=0.1,xlab="GC Content",ylab=expression(paste("log(NRC"["lib"],"+0.01)",sep="")))
lines(RC_DT$GC,predictions1,col = "red")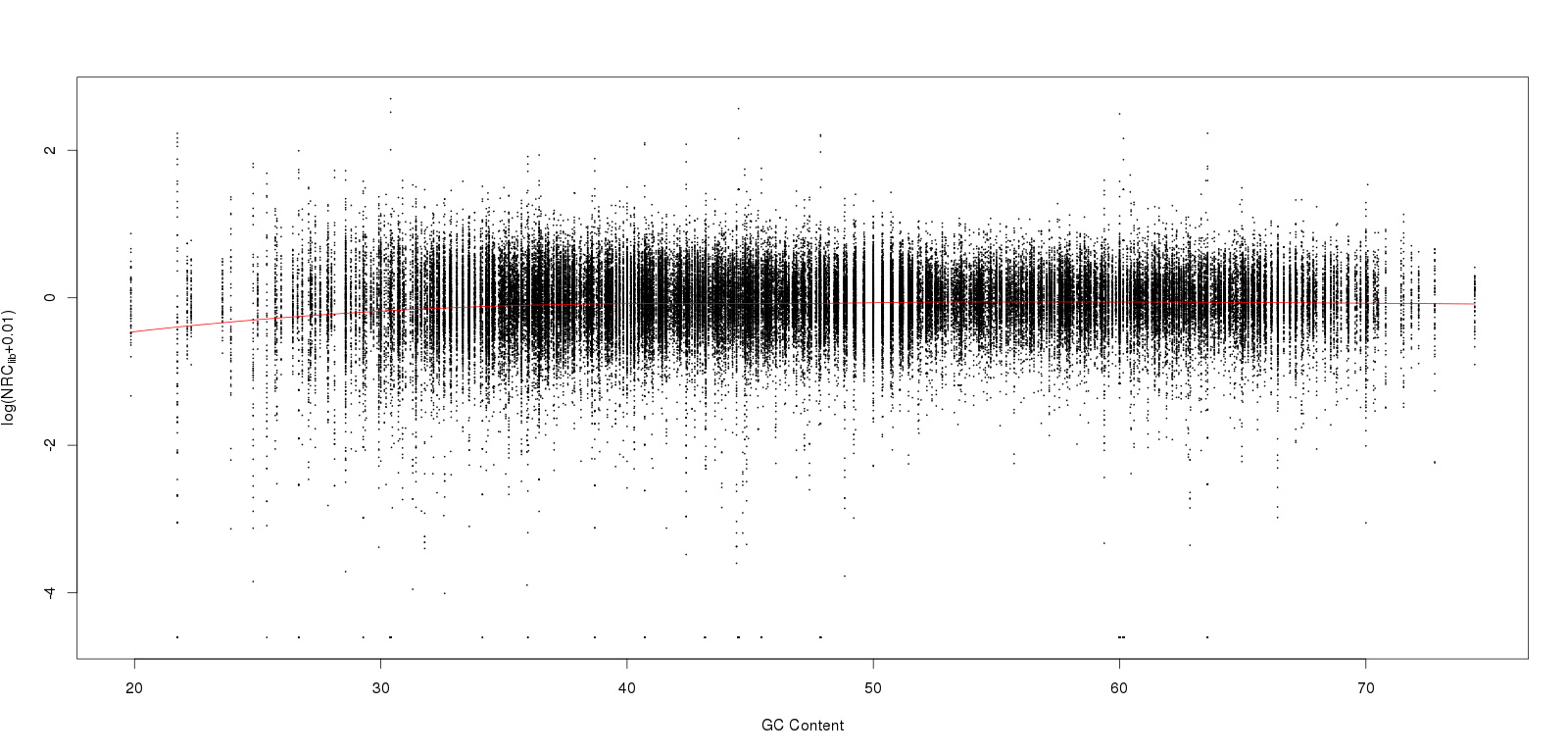

取残差，去除GC含量对深度的影响

#sustract the influence of GC
resi <- log(RC_DT$RC+0.01)-predictions1
RC_DT$RC <- resi
setkey(RC_DT,GC)

此时RC_DT$RC就是normalize之后的RC
画图显示nomalize之后的RC,并将拟合的loess曲线和normalize之后的数据保存

#plot scatter and line using Norm GC data
plot(RC_DT$GC,RC_DT$RC,cex=0.1,xlab="GC Content",ylab=expression("NRC"["GC"]))
gcCount.loess <- loess(RC~GC,data=RC_DT,control = loess.control(surface = "direct"),degree=2)
save(gcCount.loess,file="/home/ywliao/project/Gengyan/gcCount.loess.Robject")
predictions2 <- predict(gcCount.loess,RC_DT$GC)
lines(RC_DT$GC,predictions2,col="red")
save(RC_DT,file="/home/ywliao/project/Gengyan/RC_DT.Rdata")

当然，也想看一下amplicon 长度len 对RC的影响，不过影响不大

全部代码如下(经过修改，可能与上面完全匹配)：

library(data.table)load("/home/ywliao/project/Gengyan/RC_DT.Rdata")
RRC_DT <- RC_DT[Type=="WBC" & !is.na(RC),]lst <- list()
for (Samp in unique(RC_DT$Sample)){
RC_DT <- RRC_DT[Sample==Samp]
####loess GC vs RC####
gcCount.loess <- loess(log(RC+0.01)~GC,data=RC_DT,control = loess.control(surface = "direct"),degree=2)
predictions1<- predict (gcCount.loess,RC_DT$GC)
#plot scatter and line 
#plot(RC_DT$GC,log(RC_DT$RC+0.01),cex=0.1,xlab="GC Content",ylab=expression(paste("log(NRC"["lib"],"+0.01)",sep="")))
#lines(RC_DT$GC,predictions1,col = "red")
#sustract the influence of GC
resi <- log(RC_DT$RC+0.01)-predictions1
RC_DT$NRC <- resi
setkey(RC_DT,GC)
#plot scatter and line using Norm GC data
#plot(RC_DT$GC,RC_DT$NRC,cex=0.1,xlab="GC Content",ylab=expression("NRC"["GC"]))
gcCount.loess <- loess(NRC~GC,data=RC_DT,control = loess.control(surface = "direct"),degree=2)
predictions2 <- predict(gcCount.loess,RC_DT$GC)
#lines(RC_DT$GC,predictions2,col="red")
lst[[Samp]] <- RC_DT
}
NRC_DT <- rbindlist(lst)
save(RC_DT,file="/home/ywliao/project/Gengyan/NRC_DT.Rdata")####loess len vs RC###
setkey(RC_DT,Len)
len.loess <- loess(RC_DT$NRC~RC_DT$Len, control = loess.control(surface = "direct"),degree=2)
predictions2<- predict (len.loess,RC_DT$Len)
#plot scatter and line 
plot(RC_DT$Len,RC_DT$NRC,cex=0.1,xlab="Length",ylab=expression(paste("log(RC"["GC"],"+0.01)",sep="")))
lines(RC_DT$Len,predictions2,col = "red")