网络模型 - 随机网络,无标度网络,分层网络
转自: http://www.flickr.com/photos/caseorganic/4510691991/in/set-72157624621620243
小图

大图

Network Models - Random network, Scale-free network, Hierarchical network
随机网络
The Erdös–Rényi (ER) model of a random network14 (see figure, part A) starts with N nodes and connects each pair of nodes with probability p,
which creates a graph with approximately pN(N–1)/2 randomly placed links (see figure, part Aa). The node degrees follow a Poisson distribution
(see figure, part Ab), which indicates that most nodes have approximately the same number of links (close to the average degree ). The tail
(high k region) of the degree distribution P(k) decreases exponentially, which indicates that nodes that significantly deviate from the average are
extremely rare. The clustering coefficient is independent of a node’s degree, so C(k) appears as a horizontal line if plotted as a function of k (see
figure, part Ac). The mean path length is proportional to the logarithm of the network size, l ~ log N, which indicates that it is characterized by the
small-world property.
无标度网络
Scale-free networks (see figure, part B) are characterized by a power-law degree distribution; the probability that a node has k links follows
P(k) ~ k –γ, where γ is the degree exponent. The probability that a node is highly connected is statistically more significant than in a random graph,
the network’s properties often being determined by a relatively small number of highly connected nodes that are known as hubs (see figure, part
Ba; blue nodes). In the Barabási–Albert model of a scale-free network15, at each time point a node with M links is added to the network, which
connects to an already existing node I with probability ΠI = kI/ΣJkJ, where kI is the degree of node I (FIG. 3) and J is the index denoting the sum over
network nodes. The network that is generated by this growth process has a power-law degree distribution that is characterized by the degree
exponent γ = 3. Such distributions are seen as a straight line on a log–log plot (see figure, part Bb). The network that is created by the
Barabási–Albert model does not have an inherent modularity, so C(k) is independent of k (see figure, part Bc). Scale-free networks with degree
exponents 2<γ<3, a range that is observed in most biological and non-biological networks, are ultra-small34,35, with the average path length
following ~ log log N, which is significantly shorter than log N that characterizes random small-world networks.
分层网络
To account for the coexistence of modularity, local clustering and scale-free topology in many real systems it has to be assumed that clusters
combine in an iterative manner, generating a hierarchical network47,53 (see figure, part C). The starting point of this construction is a small cluster
of four densely linked nodes (see the four central nodes in figure, part Ca).Next, three replicas of this module are generated and the three external
nodes of the replicated clusters
connected to the central node of
the old cluster, which produces a
large 16-node module. Three
replicas of this 16-node module
are then generated and the 16
peripheral nodes connected to
the central node of the old
module, which produces a new
module of 64 nodes. The
hierarchical network model
seamlessly integrates a scale-free
topology with an inherent
modular structure by generating
a network that has a power-law
degree distribution with degree
exponent γ = 1 + n4/n3 = 2.26
(see figure, part Cb) and a large,
system-size independent average
clustering coefficient ~ 0.6.
The most important signature of
hierarchical modularity is the
scaling of the clustering
coefficient, which follows
C(k) ~ k –1 a straight line of slope
–1 on a log–log plot (see figure,
part Cc). A hierarchical
architecture implies that sparsely
connected nodes are part of
highly clustered areas, with
communication between the
different highly clustered
neighbourhoods being
maintained by a few hubs
(see figure, part Ca).
From Network Biology - Understanding the Cell's Functional Organization. Albert Laszlo Barabasi, Zoltan Oltvai 2004.
About the Authors
Albert-László Barabási is the Emil T. Hofman Professor of physics
at the University of Notre Dame, USA. His research group introduced
the concept of scale-free networks and studied their relevance
to biological and communication systems. He obtained his
M.Sc. degree in physics in 1991 from Eötvös Loránd University,
Budapest, Hungary, and his Ph.D. in 1994 from Boston University,
USA. After a year as a postdoctoral fellow at IBM Thomas J.
Watson Research Center, USA, he joined the University of Notre
Dame in 1995. He is a fellow of the American Physical Society, and
the author of the general audience book Linked: The New Science of
Networks.
Zoltán Nagy Oltvai is an assistant professor of pathology at
Northwestern University’s Feinberg School of Medicine, USA. His
clinical interest is molecular pathology and he is the director of
diagnostic molecular pathology at the medical school and
Northwestern Memorial Hospital. His research group’s interest is
the theoretical and experimental study of intracellular molecular
interaction networks. He received his M.D. degree from
Semmelweiss Medical University, Budapest, Hungary, and did his
clinical pathology/molecular biology research residency at
Washington University/Barnes Hospital in St. Louis, USA.
看不懂英文的看中文的,写的还可以
参考:http://www.cnblogs.com/peon/archive/2009/08/23/1552472.html
传统的随机网络(如ER模型),尽管连接是随机设置的,但大部分节点的连接数目会大致相同,即节点的分布方式遵循钟形的泊松分布,有一个特征性的“平均数”。连接数目比平均数高许多或低许多的节点都极少,随着连接数的增大,其概率呈指数式迅速递减。故随机网络亦称指数网络。
节点连接数的泊松分布:
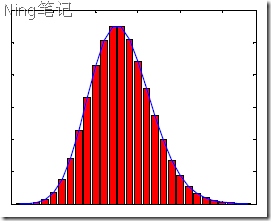
一个随机网络:
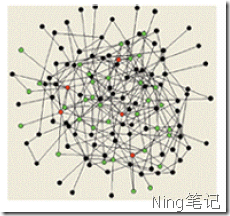
现实世界的网络大部分都不是随机网络,少数的节点往往拥有大量的连接,而大部分节点却很少,一般而言他们符合zipf定律,(也就是80/20马太定律)。人们给具有这种性质的网络起了一个特别的名字——无标度网络。这里的无标度是指网络缺乏一个特征度值(或平均度值),即节点度值的波动范围相当大。
节点连接数的zipf分布:
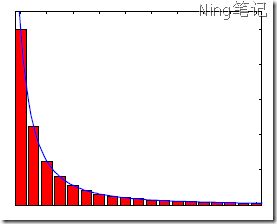
符合zipf分布的无标度网络:
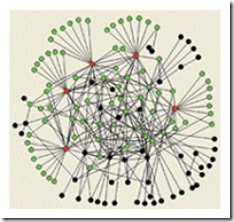
现实中的交通网,电话网和Internet都是无标度网络,在这种网络中,存在拥有大量连接的集散节点,比如交通枢纽就是这样的节点。下面是Internet的连接模型:

分布满足幂律的无标度网络还有一个奇特的性质——“小世界”特性[49],虽然WWW中的页面数已超过80亿,但平均来说,在WWW上只需点击19次超链接,就可从一个网页到达任一其它页面。“小世界”现象在社会学上也称为“六度分离”。
Barabási与Albert针对复杂网络中普遍存在的幂律分布现象,提出了网络动态演化的BA模型[42, 59],他们解释,成长性和优先连接性是无标度网络度分布呈现幂律的两个最根本的原因。所谓成长性是指网络节点数的增加,像Internet中自治系统或路由器的添加,以及WWW中网站或网页的增加等,优先连接性是指新加入的节点总是优先选择与度值较高的节点相连,比如,新网站总是优先选择人们经常访问的网站作为超链接。随着时间的演进,网络会逐渐呈现出一种“富者愈富,贫者愈贫”的现象。社会学家所说的“马太效应”[72],《新约》圣经所说的“凡有的,还要加给他,叫他有余”,同优先连接也有某种相通之处。
引用:
幂律分布研究简史
无标度网络及其系统科学意义
下面是我的其他博客:
博客园,写一些工作和学习的笔记: http://www.cnblogs.com/peon/
博客堂,开发方面的一些文章:http://blog.joycode.com/peon/
流媒体博客,流媒体方面的一些文章:http://blog.lmtw.com/b/peon/
相关文章:

一文介绍机器学习中的三种特征选择方法
作者 | luanhz来源 | 小数志导读机器学习中的一个经典理论是:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限。也正因如此,特征工程在机器学习流程中占有着重要地位。广义的特征工程一般可分为三个环节:特征提取、…

[转化率预估-1]引言
原文:hhttp://www.flickering.cn/ads/2014/06/%E8%BD%AC%E5%8C%96%E7%8E%87%E9%A2%84%E4%BC%B0%E2%80%94%E2%80%94%E5%BC%95%E8%A8%80/ 最近几年,“计算广告学”的概念风生水起,让我们这些从事在线广告匹配技术的程序猿着实荣耀了一把。这在参…

reportNG定制化之失败截图及日志
先从github上拉下 reportNg的源代码 reportng 拉下源码后我们使用IDEA进行导入 1、reportng.properties 增加部分类表项 这里我们直接在末尾添加 logLog Info screenshotScreen Shot durationDuration2、results.html.vm 修改结果的html,我们目前只修改fail的情况下…
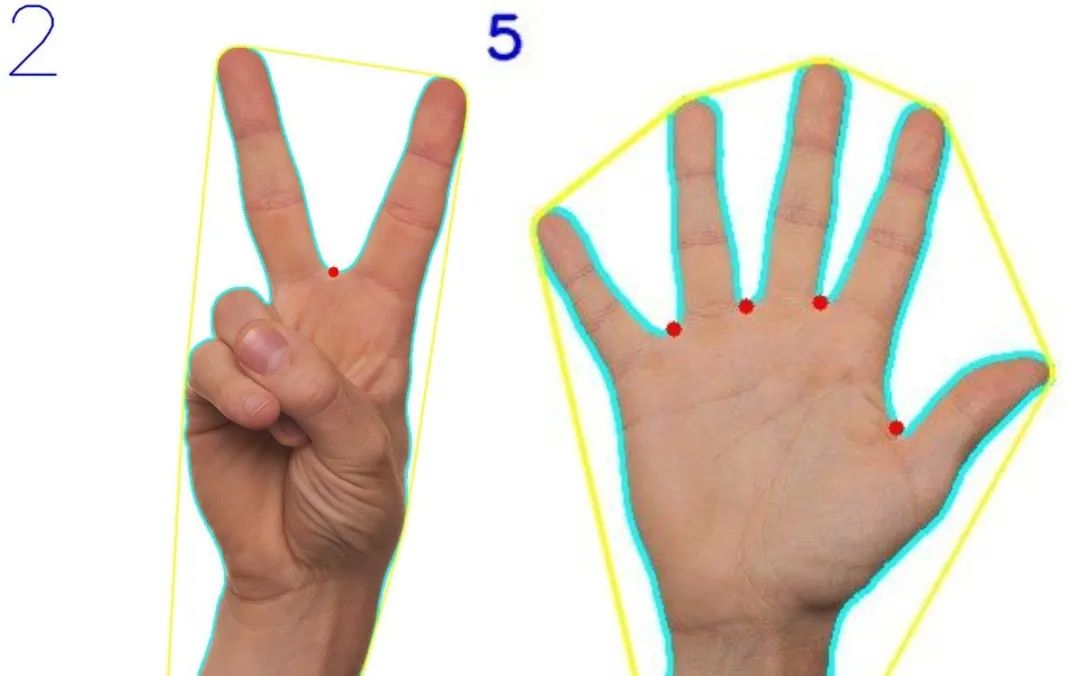
基于 OpenCV 的手掌检测和手指计数
作者 | 努比 来源 | 小白学视觉 利用余弦定理使用OpenCV-Python实现手指计数与手掌检测。 手检测和手指计数 接下来让我们一起探索以下这个功能是如何实现的。 OpenCV OpenCV(开源计算机视觉库)是一个开源计算机视觉和机器学习软件库。OpenCV的构建旨在为…

side menu待研究
2019独角兽企业重金招聘Python工程师标准>>> http://fontawesome.bootstrapcheatsheets.com/ http://www.queness.com/post/14666/recreate-google-nexus-menu http://www.jqueryscript.net/demo/Sliding-Side-Menu-Panel-with-jQuery-Bootstrap-BootSideMenu/ &a…
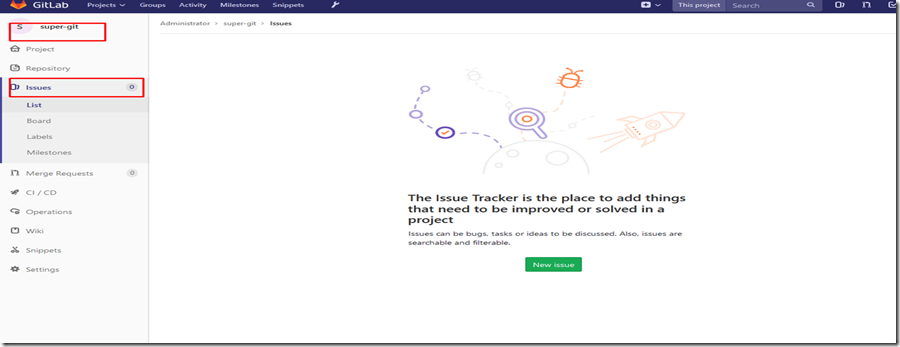
Gitlab Issue Tracker and Wiki(一)
本节内容:创建第一个问题创建第一个合并请求接受合并请求工作里程碑在提交中引用问题创建维基百科页使用Gollum管理维基百科一. 创建问题1. 登陆Gitlab服务器2. 切换到想要创建问题的项目3. 点击Issues.4. 点击【New issue】5. 根据情况进行填写。二. 创建合并请求1…

runtime实践之Method Swizzling
利用 Objective-C 的 Runtime 特性,我们可以给语言做扩展,帮助解决项目开发中的一些设计和技术问题。这一篇,我们来探索一些利用 Objective-C Runtime 的黑色技巧。这些技巧中最具争议的或许就是 Method Swizzling 。 介绍一个技巧࿰…

网络协议关系拓扑图 很全面 很好
NETWORK ASSOCIATES GUIDE TO COMMUNICATIONS PROTOCOLS 网络协议关系拓扑图 很全面 很好 值得收藏!

一行代码搞定 Python 逐行内存消耗分析
作者 | 费弗里来源 | Python大数据分析我们即将学习的是:一行代码分析Python代码行级别内存消耗。很多情况下,我们需要对已经写好的Python程序的内存消耗进行优化,但是一段代码在运行过程中的内存消耗是动态变化的,这种时候就可以…

崛起于Springboot2.X之Mybatis-全注解方式操作Mysql(4)
为什么80%的码农都做不了架构师?>>> 1、使用注解方式对mysql增删改查,它很方便,不像一些逆向工程工具一样生成的都是乱七八糟,虽然很全的方法,完全手写sql 基于上一篇博客,我们只需要新建一个目录dao层&am…

hdu 1247
Problem DescriptionA hat’s word is a word in the dictionary that is the concatenation of exactly two other words in the dictionary.You are to find all the hat’s words in a dictionary.InputStandard input consists of a number of lowercase words, one per li…

php执行URL解析
方法一: $url"http://www.baidu.com";file_get_contents($url);方法二: // CURL 方法$url"http://www.baidu.com";$ch curl_init( );curl_setopt( $ch,CURLOPT_URL,$url );curl_setopt( $ch,CURLOPT_HEADER,0 );curl_setopt( $ch,…

Python 来分析,堪比“唐探系列”!B站9.5分好评如潮!
作者 | 菜鸟哥来源 | 菜鸟学PythonHello 小伙伴们,最近一部非常不错的悬疑侦探喜剧 电影,登上B站热榜!菜鸟哥看完之后,大呼过瘾,简直就是一本非常棒的"剧本杀"!演员都是实力派,演技超…

10进制转换为二十六进制字符串A-Z
def convert10to26(num): ...: 10进制转为26进制字母 A-Z, 输入参数10进制数num, 返回26位的字母A-Z 参数type: num: int return: str ...: ...: digit_list [] # 列表当栈使用,存储每次求余的结果 ...: while num !0: ...: digit_list.append(num%26)…

从hello world 说程序运行机制
http://www.cnblogs.com/yanlingyin/archive/2012/03/05/2379199.html 开篇 学习任何一门编程语言,都会从hello world 开始。对于一门从未接触过的语言,在短时间内我们都能用这种语言写出它的hello world。然而,对于hello world 这个简单程序…

爱耳日腾讯天籁行动再升级 助力100位青年听障人才打破“屏障”
公益是解决社会问题的重要切入口,科技是提升效率的强有力工具。当产业技术走入公益场景,科技也在发挥更大的社会价值。 《中国听力健康报告(2021)》显示,过度的噪音曝露,正让全球11亿年轻人面临听力受损的风…

IOS推送详解
为什么80%的码农都做不了架构师?>>> IOS推送详解 一.关于推送通知 推送通知,也被叫做远程通知,是在iOS 3.0以后被引入的功能。是当程序没有启动或不在前台运行时,告诉用户有新消息的一种途径,是从外部服务…

redis(4)
redis-cli -p 6380redis-cli -p 6379 info server | grep run_idpsync ? -1

PHP也玩并发,巧用curl 并发减少后端访问时间
说明:本人源自3篇博文 http://blog.csdn.net/zuiaituantuan/article/details/7048782首先,先了解下 php中的curl多线程函数:# curl_multi_add_handle# curl_multi_close# curl_multi_exec# curl_multi_getcontent# curl_multi_info_read# cur…
ADSL自动更换IP地址源代码
有些网站限制IP地址,什么一个IP地址只能一次之类的。特别是投票网址,为了防止刷票,限制1个IP只允许投票一次! 此程序采用Vs2010C#开发,提供全部源代码!方便程序猿朋友二次开发! 可以后台运行&am…
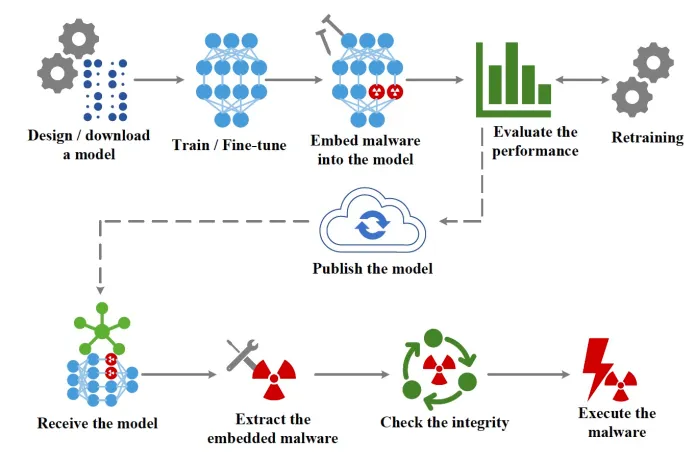
安全隐患:神经网络可以隐藏恶意软件
编译 | 禾木木 出品 | AI科技大本营(ID:rgznai100) 凭借数百万和数十亿的数值参数,深度学习模型可以做到很多的事情,例如,检测照片中的对象、识别语音、生成文本以及隐藏恶意软件。加州大学圣地亚哥分校和伊利诺伊大学…

实现一个完美符合Promise/A+规范的Promise
原文在我的博客中:原文地址 如果文章对您有帮助,您的star是对我最好的鼓励~ 简要介绍:Promise允许我们通过链式调用的方式来解决“回调地狱”的问题,特别是在异步过程中,通过Promise可以保证代码的整洁性和…

用递归法计算斐波那契数列的第n项
斐波纳契数列(Fibonacci Sequence)又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F00,F11,FnF(n-1)F(n-2)&a…

ArrayList的内存泄露
2019独角兽企业重金招聘Python工程师标准>>> 大家先运行下下面这段代码,看看结果 public class MemoryLeak {public static void main(String[] args) throws InterruptedException {new Thread(new Runnable() {Overridepublic void run() {for (int i …

给 Python 初学者推荐的 IDE 哦!
作者 | 黄伟呢来源 | 数据分析与统计学之美总有一些Python初学者,会问到:学习Python,应该用什么Python IDE?了解到他们使用Python做什么之后,我总结了这篇文章。IDE是集成开发环境的缩写,通俗地说ÿ…

django 2.0路由配置变化
urlpatterns变量的语法 urlpatterns应该是path()和/或re_path()实例的Python列表。 首先,Django会使用根路由解析模块(root URLconf)来解析路由。 通常,这是ROOT_URLCONF设置的值,但是如果传入的HttpRequest对象具有urlconf属性ÿ…

用ext_skel,实现一个PHP扩展,添加到PHP并调用
http://www.shinrun.com/PHP 一、开始之前 1. 系统环境:FreeBSD 8.22. AP环境:即已经装好的Apache2.2.17、PHP5.3.8环境3. PHP源码:下载稳定版本源码到当前用户的目录,如,下载PHP 5.3.8到/usr/home/abc下。4. 其它要求…

关于第三方IOS的checkBox框架的使用
关于第三方IOS的checkBox框架的使用 这个框架是从github上下载获取的:M13Checkbox。 只是github的源码项目工程比较久远,所以我把代码部分拷贝到XCode 7.1.0新建的项目里。 下面是展示效果 客户端源码使用参考: 1 #import "ViewControll…

20 个 Pandas 数据实战案例,干货多多
作者 | 俊欣来源 | 关于数据分析与可视化今天我们讲一下pandas当中的数据过滤内容,小编之前也写过也一篇相类似的文章,但是是基于文本数据的过滤,大家有兴趣也可以去查阅一下。下面小编会给出大概20个案例来详细说明数据过滤的方法࿰…

Python创建和访问字典
>>> dict1 {a:1,b:2,c:3,d:4}>>> print(a的值是:,dict1[a])a的值是: 1>>> dict4 dict(我 快乐, 你 伤悲)SyntaxError: keyword cant be an expression>>> dict4[你] 改变悲伤>>> dict4{我: 快乐, 你: 改变悲伤}>>>…
