Depth graph
深度相机
定义:可以直接获取场景中物体距离摄像头物理距离的相机。在计算机视觉系统中,三维场景信息为图像分割、目标检测、物体跟踪等各类计算机视觉应用提供了更多的可能性,而深度图像(Depth map)作为一种普遍的三维场景信息表达方式得到了广泛的应用。深度图像的每个像素点的灰度值可用于表征场景中某一点距离摄像机的远近。
获取深度图像的方法可以分为两类:被动测距传感和主动深度传感。
In short:深度图像的像素值反映场景中物体到相机的距离,获取深度图像的方法=被动测距传感+主动深度传感
被动测距传感
被动测距传感中最常用的方法是双目立体视觉,该方法通过两个相隔一定距离的不同视角的摄像机获取同一场景的两幅图像,通过立体匹配算法找到两幅图像中对应的像素点,随后根据三角原理计算出视差信息,而视差信息通过转换可用于表征场景中物体的深度信息。基于立体匹配算法,还可通过拍摄同一场景下不同角度的一组图像来获得该场景的深度图像。此外,场景深度信息还可以通过对图像的光度特征 、明暗特征 、几何特征等特征进行分析间接估算得到。
上图展示了Middlebury Stereo Dataset中Tsukuba场景的彩色图像、视差实际值与用Graph cuts算法得到的立体匹配误差估计结果,该视差图像可以用于表征场景中物体的三维信息。 可以看到,通过立体匹配算法得到的视差图虽然可以得到场景的大致三维信息,但是部分像素点的视差存在较大误差。双目立体视觉获得视差图像的方法受限于基线长度以及左右图像间像素点的匹配精确度,其所获得的视差图像的范围与精度存在一定的限制。
In short, 常用于深度图像增强领域的测试数据集Middlebury Stereo Dataset属于被动测距传感;
被动测距传感=两个相隔一定距离的相机获得两幅图像+立体匹配+三角原理计算视差(disparity)
双目立体视觉测距的原理和人眼类似,通过计算空间中同一个物体在两个相机成像的视差就可以根据如下三角关系计算得到物体离相机的距离:
但是算法实现比较困难,双目立体视觉测距算法的核心就是寻找对应关系。可以理解为给定一个相机拍摄的图片中的任意一个像素点,如何在另外一个相机拍摄的图像中找到和它对应的像素点,这个过程需要特征提取、特征匹配等一系列复杂的算法。但是由于光照变化、光线明暗等外在因素的影响,拍摄的两张图片差别可能比较大,这会对特征匹配算法提出很大的挑战。
另外,如果拍摄的物体缺乏纹理和细节(比如拍摄一张白纸)的话,也很难进行特征匹配。这些都对算法的鲁棒性提出了很大的挑战。
虽然TOF相机和双目立体视觉都能实现测距的功能,但是它们还是有很大不同表格如下

下表是双目立体视觉、结构光、TOF三种可以测量深度(距离)的技术方案综合比较:双目视觉 Vs 结构光 Vs TOF
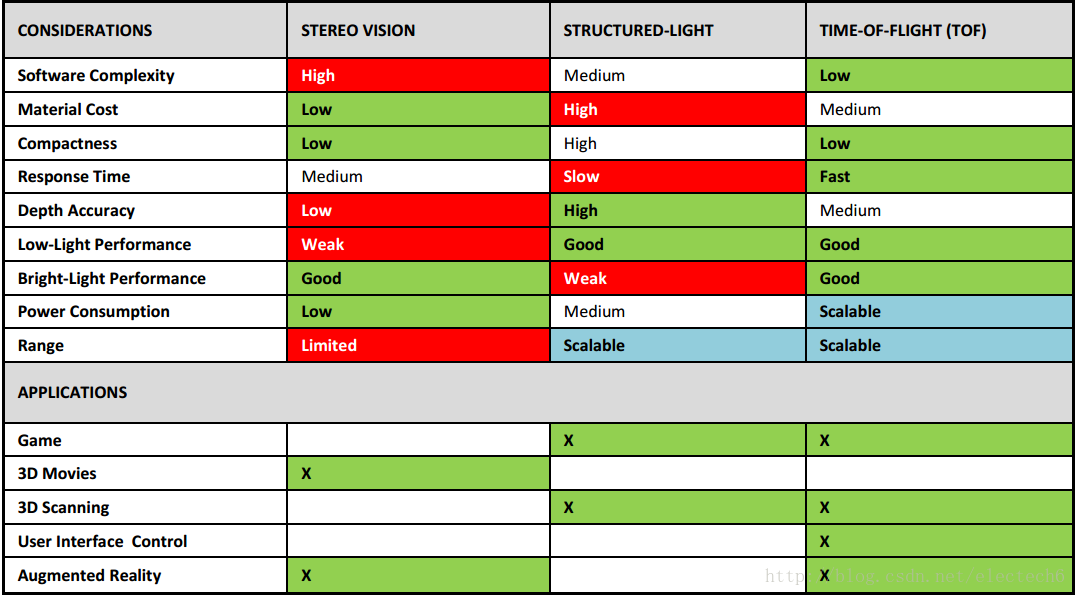
从上述的对比分析来看,TOF方案具有响应速度快,深度信息精度高,识别距离范围大,不易受环境光线干扰等优势。因此想要在移动端直接实现深度的测量,最有竞争力的就是TOF方案了。
深度相机应用:范围非常广泛:手势识别,以及活体人脸识别、空间测距、三维重建、AR(增强现实)等领域。
1、手势识别。
TOF深度相机可以将人脸、身体、手臂、手指从背景中分离,并且这种分割置信度较高,不受自然光变化的影响,同时能够实时性处理,所以这将在智能交互领域大有用武之地。预计最近几年会迅速进入消费级电子产品中。


2、真实的AR游戏体验。
如下图是Phab 2的AR游戏展示。由于在二维图像中融合了实时的深度信息,所以AR游戏的体验比较真实。比如虚拟出来的一只猫,通过实时的空间深度感知,它可以“感受”到空间的相对位置关系,当它走到桌子边缘的时候,会很自然地跳到地面上,这在之前的AR游戏中是难以实现的。

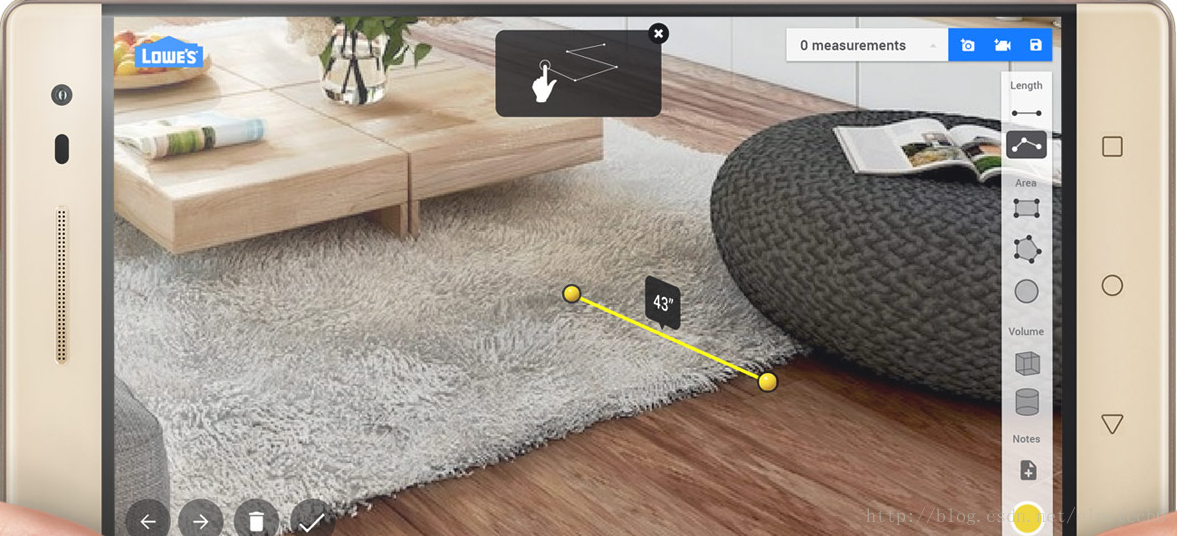
3、三维空间测量。
由于能够实时获得深度信息,所以实现三维空间测量也是顺其自然的。比如在室内装修领域,可以方便的将各种虚拟的家具以真实的尺寸摆放到现实环境中,用户拿着手机就可以体验家居放在室内的360°真实效果,这无疑将是一个令人激动的应用场景。
4、三维扫描/重建。
可以用于三维物体和k建模和机器人视觉导航和定位。比如你看到一座非常喜欢的雕塑,就可以利用手机上的彩色相机+深度相机对它扫描一周,结合相应的算法就可以生成该雕塑的三维模型数据,利用三维打印机就可以方便的打印出一个三维的雕塑复制品出来。

5、更广泛的其他应用。
融入了深度信息的三维影像可以用于活体人脸识别,避免传统二维人脸识别的安全隐患;可以更加方便进行人体三维测量,从而推动虚拟在线试衣行业的发展等。

随着深度测量技术的发展,必然还有出现更多有趣的应用场景。
深度信息融合
当我们获得了深度图后,下一步就是要把深度信息融合到普通RGB相机拍摄的彩色图片。这一步需要强大的算法来保障。深度信息融合难的原因:
1、深度相机的分辨率目前还比较低,一般都是VGA(640 x 480)以下。而现在普通的RGB相机分辨率都已经到千万像素级以上了,是深度相机分辨率的几十倍甚至上百倍。因此需要将低分辨的深度图变成和RGB相机一致的高分辨率,这种“从无到有”的分辨率提升需要利用彩色图中物体的纹理、边界等内容信息,这个过程要想保持细节是比较困难的。
2、深度相机和彩色相机融合时还需要知道两个相机的畸变系数、光学中心、相对旋转/平移量等一系列参数,这就需要对两个相机进行相机标定工作。而深度相机的低分辨率对于相机标定工作也是一个较大的挑战。
主动测距传感
主动测距传感相比较于被动测距传感最明显的特征是:设备本身需要发射能量来完成深度信息的采集。这也就保证了深度图像的获取独立于彩色图像的获取。近年来,主动深度传感在市面上的应用愈加丰富。主动深度传感的方法主要根据原理不同,主要有飞行时间(TOF)、结构光、激光扫描几种方式(注:有些地方将双目立体视觉相机也列为深度相机的一种,它是单纯依靠算法计算得到的深度信息)。
TOF相机
TOF相机获取深度图像的原理是:通过对目标场景发射连续的近红外脉冲,然后用传感器接收由物体反射回的光脉冲。通过比较发射光脉冲与经过物体反射的光脉冲的相位差,可以推算得到光脉冲之间的传输延迟进而得到物体相对于发射器的距离,最终得到一幅深度图像。
TOF相机内部每个像素经过上述过程都可以得到一个对应的距离,所有的像素点测量的距离就构成了一幅深度图,如下图所示。左边是原图,右边是对应的深度图。

可以看到深度图其实是一张灰度图,它是一张三维的图:水平垂直坐标对应像素位置,该位置的灰度值对应的是该像素距离摄像头的距离。所以深度图中的每个像素可以表示空间中一个点的三维坐标,所以深度图中的每个像素也称为体像素(voxel)。
TOF相机所获得的深度图像有以下的缺陷:
1. 深度图像的分辨率远不及彩色图像的分辨率
2. 深度图像的深度值受到显著的噪声干扰
3. 深度图像在物体的边缘处的深度值易出现误差,而这通常是由于一个像素点所对应的场景涵盖了不同的物体表面所引起的。
除此之外,TOF相机的通常价格不菲。

结构光与Kinect
结构光是具有特定模式的光,其具有例如点、线、面等模式图案。
基于结构光的深度图像获取原理是:将结构光投射至场景,并由图像传感器捕获相应的带有结构光的图案。由于结构光的模式图案会因为物体的形状发生变形,因此通过模式图像在捕捉得到的图像中的位置以及形变程度利用三角原理计算即可得到场景中各点的深度信息。结构光测量技术提供了高精度并且快速的三维信息,其在汽车、游戏、医疗等领域均已经得到了广泛的应用。
基于结构光的思想,微软公司推出了一款低价优质的结合彩色图像与深度图像的体感设备Kinect,该设备被应用于如人机交互(Xbox系列游戏机)、三维场景重建、机器视觉等诸多领域。

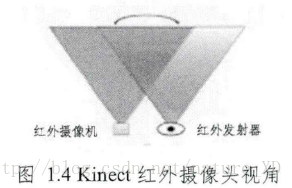
微软公司的Kinect有三个镜头,除了获取RGB彩色图像的摄像机之外,左右两边的镜头分别是红外线发射器和红外线CMOS摄像机,这两个镜头共同构成了Kinect的深度传感装置,其投影和接收区域相互重叠,如下图所示。
Kinect采用了一种名为光编码(Light Coding)的技术,不同于传统的结构光方法投射一幅二维模式图案的方法,Kinect的光编码的红外线发射机发射的是一个具有三维纵深的“立体编码”。光编码的光源被称为激光散斑,其形成原理是激光照射到粗糙物体或穿透毛玻璃后得到了随机的衍射斑点。激光散斑具有高度的三维空间随机性。当完成一次光源标定后,整个空间的散斑图案都被记录,因此,当物体放进该空间后,只需得知物体表面的散斑图案,就可以知道该物体所处的位置,进而获取该场景的深度图像。红外摄像机捕获的红外散斑图像如下图所示,其中左侧的图片展现了右侧图片中框中的细节。
Kinect低廉的价格与实时高分辨率的深度图像捕捉特性使得其在消费电子领域得到了迅猛发展,然而Kinect的有效测距范围仅为800毫米到4000毫米,对处在测距范围之外的物体,Kinect并不能保证准确深度值的获取。Kinect捕获的深度图像存在深度缺失的区域,其体现为深度值为零,该区域意味着Kinect无法获得该区域的深度值。而除此之外,其深度图像还存在着深度图像边缘与彩色图像边缘不对应、深度噪声等问题。Kinect所捕获的彩色图像与深度图像如下图所示。
Kinect所捕获的深度图像产生深度缺失区域的原因多种多样。除了受限于测距范围,一个重要的原因是目标空间中的一个物体遮挡了其背后区域。这种情况导致了红外发射器所投射的图案无法照射到背后区域上,而背后区域却有可能被处在另一个视角的红外摄像机捕捉到,然而该区域并不存在散斑图案,该区域的深度信息也就无法被获得。物体表面的材质同样会影响Kinect深度图像的获取。当材质为光滑的平面时,红外投射散斑光束在物体表面产生镜面反射,红外摄像机无法捕捉该物体反射的红外光,因此也就无法捕获到该表面的深度;当材质为吸光材料时,红外投射散斑被该表面所吸收而不存在反射光,红外摄像机同样无法捕捉到该表面的深度信息。【材质对深度缺失的影响,分析到位】除此之外,Kinect所捕获的深度图像存在的与彩色图像边缘不一致的问题主要是由彩色摄像机与红外摄像机的光学畸变引起的。
激光雷达
激光雷达测距技术通过激光扫描的方式得到场景的三维信息。其基本原理是按照一定时间间隔向空间发射激光,并记录各个扫描点的信号从激光雷达到被测场景中的物体,随后又经过物体反射回到激光雷达的相隔时间,据此推算出物体表面与激光雷达之间的距离。
激光雷达由于其测距范围广、测量精度高的特性被广泛地用于室外三维空间感知的人工智能系统中,例如自主车的避障导航、三维场景重建等应用中。下图展示的是激光雷达Velodyne HDL-64E在自主车中的应用,该激光雷达能够获取360°水平方向上的全景三维信息,其每秒能够输出超过130万个扫描点的数据。全向激光雷达曾在美国举办的DARPA挑战赛中被许多队伍所采用,其也成为了自主行驶车辆的标准配置。
相关文章:

【ACM】POJ 1852
【问题描述】 一队蚂蚁在一根水平杆上行走,每只蚂蚁固定速度 1cm/s. 当一只蚂蚁走到杆的尽头时,立即从秆上掉落. 当两只蚂蚁相遇时它们会掉头向相反的方向前进. 我们知道每只蚂蚁在杆上的初始位置, 但是, 我们不知道蚂蚁向哪个方向前行. 你的任务是计算…

ZStack--通过Ansible实现全自动化
2019独角兽企业重金招聘Python工程师标准>>> Agent是一种常见的IaaS软件管理设备的方式;例如,ZStack使用Python agents去管理KVM主机。因为海量的设备,安装和升级agents成为巨大的挑战,所以大多数IaaS软件把这个问题留…
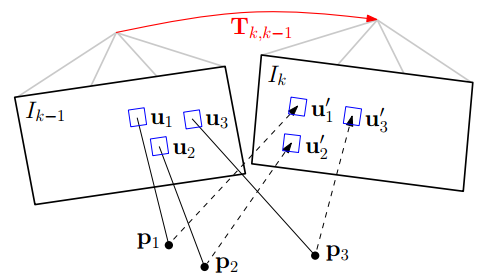
SVO 半直接视觉里程计
SVO 从名字来看,是半直接视觉里程计,所谓半直接是指通过对图像中的特征点图像块进行直接匹配来获取相机位姿,而不像直接匹配法那样对整个图像使用直接匹配。整幅图像的直接匹配法常见于RGBD传感器,因为RGBD传感器能获取整幅图像的…

css构造文本
1. 1. 文本缩进text-indent:值;值为数字,最常用的数值单位是px(像素),也可以直接是百分比!text-indent:100px;text-indent:10%;2. 文本对齐text-align:对其方式;可以的值为:left、center、right3. 文本行高…

【数据结构】单链表的逆序输出(两种方法)
第一种方法:转换指针方向 即:将一个已经创建好的单链表进行指针域的改变 今天突然被问到单链表逆序的问题,弄了好久才看出别人的程序有啥问题,就重新写了一遍。 今天才在CSDN客户端上看到美团的面试题是冒泡排序。 一个看似简单…

koa+mongoose基础入门
1.mongoose基本使用 1.安装mongodb npm install mongodb 2.引入mongodb数据表,连接mongodb,通过node来对mongodb进行异步的增删改查 const mongodb requrie(mongodb); mongodb.MongoClient.connect("mongodb://localhost/db1", function(err,…

视觉SLAM学习(三)--------SLAM 综述
SLAM概述 参考资料分享来自本人博客:https://blog.csdn.net/Darlingqiang/article/details/78840931 SLAM一般处理流程包括track和map两部分。所谓的track是用来估计相机的位姿,也叫front-end。而map部分(back-end)则是深度的构建,通过前面…
【数据结构】所有顶点对的最短路径 Floyd算法
所有顶点对的最短路径问题是指:对于给定的有向图G(V,E),求任意一对顶点之间的最短路径。 可以求解得到的 的递推公式: #include <stdio.h> #include <stdlib.h> const int FINITY 5000; const int M 20; typedef struct {ch…

backbone学习总结(二)
今天来看下backbone的路由控制的功能。其实个人感觉backbone,模块就那么几个,熟悉它的框架结构,以及组成,就差不多。 废话不多说,我们来看看还剩下的功能。 关于路由和历史管理 通过 Backbone.Router.extend 来创建路由…

人工智能--野人过河
课程简介 人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。人工智能的定义可以分为两部分,即“人工”和“智能”。“人工”比较好…

java对cookie的操作
原文:http://www.cnblogs.com/muzongyan/archive/2010/08/30/1812552.html java对cookie的操作比较简单,主要介绍下建立cookie和读取cookie,以及如何设定cookie的生命周期和cookie的路径问题。 建立一个无生命周期的cookie,即随着…

【ACM】POJ 3069
【问题描述】 Saruman the White must lead his army along a straight path from Isengard to Helm’s Deep. To keep track of his forces, Saruman distributes seeing stones, known as palantirs, among the troops. Each palantir has a maximum effective range of R u…

sparkCore源码解析之思维脑图
2019独角兽企业重金招聘Python工程师标准>>> 在学习sparkCore时,有几个模块的概念理解不是很透彻,故对照源码进行学习,并将结果一脑图的形式呈现,方便后续的持续学习。 详细内容见: sparkCore源码解析之blo…

pangilin 安装编译
make pangolin 的时候报错 ootsun:/home/sun/AR/orb/Pangolin-0.5/build# make [ 1%] Building CXX object src/CMakeFiles/pangolin.dir/log/packetstream.cpp.o /home/sun/AR/orb/Pangolin-0.5/src/log/packetstream.cpp: 在函数‘void pangolin::WaitUntilPlaybackTim…

PHP实现求阶乘
function factorial ($x){if ($x > 1) {$s $x * factorial ($x - 1);} else {$s $x;}return $s; }$x 100;echo $x."的阶乘的为".factorial($x);转载于:https://blog.51cto.com/chensenlin/1854679

【ACM】杭电OJ 2064(汉诺塔III)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid2064 思路: 1、将n-1个盘从A移到C f(n-1)次 2、将第n个从A移到B 1次 3、将n-1个盘从C移到A f(n-1)次 4、将第n个从B移到C 1次 5、将n-1个盘从A移到C f(n-1)次 #include<cstdio> #inclu…

文件上传至阿里云
public static String uploadFile2OSS(InputStream instream, String fileName) throws IOException {String imageName null;OSSClient ossClient null;try {ClientConfiguration conf new ClientConfiguration();// 请求超时时间设置conf.setConnectionTimeout(5000);// 请…

ORB-SLAM2安装
安装顺利与否可能会与Ubuntu版本有关。(ubuntu16.04 gcc4.8.5这个很重要偶,本班的直接决定Pangolin能不能安装成功,如果遇到哦问题的朋友可以参考一下链接 http://blog.csdn.net/Darlingqiang/article/details/78928873)亲测可用…

iOS 系统分析(一) 阅读内核准备知识
原文出自【听云技术博客】:http://blog.tingyun.com/web/a... 0x01 iOS体系架构1.1 iOS 系统的整体体系架构 用户体验( The User Experience layer ):SpringBoard 同时支持 Spotlight。 应用软件开发框架(The Application Frameworks layer&a…

【数据结构】拓扑排序
如果一个有向图中没有包含简单的回路,这样的图为有向无环图。 图中的顶点代表事件(活动),图中的有向边说明了事件之间的先后关系。这种用顶点表示活动,用弧表示活动时间的优先关系的有向图称为顶点表示活动的网&#…

Java8自定义条件让集合分组
** 将一个指定类型对象的集合按照自定义的一个操作分组; 每组对应一个List、最终返回结果类型是:List<List<T>> param <T>*/static class GroupToList<T> implements Collector<T, List<List<T>>, List<List<T>&g…
ROS_Kinetic ubuntu 16.04
ROS_Kinetic系列学习(一),在ubuntu 16.04安装ROS Kinetic。 http://wiki.ros.org/kinetic/Installation/Ubuntu 通过网页快速了解Linux(Ubuntu)和ROS机器人操作系统,请参考实验楼在线系统如下: 纯净定制版镜像已经…

android 获取手机GSM/CDMA信号信息,并获得基站信息
本文转自:http://software.intel.com/zh-cn/blogs/2011/12/16/android-gsmcdma/ 在Android中我们常用的轻松获取WIFI信号列表,那如何获取CDMA或者GSM的手机信号呢?系统提供了TelephonyManager类,此类非常丰富,基本你所…
【数据结构】关键路径
在有向图中,如果用顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间,这样的活动称为边表示活动的网,简称AOE网(Activity On Edge)。通常可以用AOE网来估算工程的完成时间,他不…
呼伦湖国家级自然保护区管理局投放草料保野生黄羊过冬
图为保护区工作人员正在观测黄羊的生活轨迹并记录数据。 王艳清 摄 图为保护区工作人员正在观测黄羊的生活轨迹并记录数据。 王艳清 摄 中新网呼伦贝尔1月16日电 (记者 李爱平)中国北方正是最为寒冷的时节,呼伦湖国家级自然保护区管理局内的60只野生黄羊正在面临食草…

buildroot httpd php
/********************************************************************* buildroot httpd php* 说明:* 在buildroot中选择了php,但是在测试的时候发现总是出现下面这行* 错误,库是存在的,但是却没有放对…

VS快速注释多行 以及 取消
快速注释多行:Ctrl K 然后 Ctrl C 快速取消多行注释 :Ctrl K 然后 Ctrl U

前端的一些小的效果
1 . 移动端字体自适应大小(暂时没用过,不过据说很有用也很好用) body{font-family: "Microsoft YaHei";font-size: 0.14rem;color: #666;max-width: 640px;margin: auto;}media screen and (min-width: 360px) { html {font-s…

Java虚拟机规范阅读(二)IEEE754简介以及Java虚拟机中的浮点算法
什么是浮点数在计算机系统的发展过程中,曾经提出过多种方法表达实数。典型的比如相对于浮点数的定点数(Fixed Point Number)。在这种表达方式中,小数点固定的位于实数所有数字中间的某个位置。货币的表达就可以使用这种方式&#…

【ACM】杭电OJ 5055(Bob and math problem)
http://acm.hdu.edu.cn/showproblem.php?pid5055 注意几点: 1、全部都是偶数,输出-1 2、n-1个是0,第n个不论是奇数,还是偶数,输出-1 3、n1的情况 4、将所有数字从大到小排列,挑出最小的奇数放在最后…