【leetcode】二叉树与经典问题

笔记

树

节点：集合

边： 关系

1对多映射

leetcode 114. 二叉树展开为链表

解法一: 后序遍历、递归

依据二叉树展开为链表的特点，使用后序遍历完成展开。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/TreeNode* last = nullptr;
class Solution {
public:void flatten(TreeNode* root) {if (root == nullptr) return;flatten(root->left);flatten(root->right);if (root->left != nullptr) {auto pre = root->left;while (pre->right != nullptr) pre = pre->right;pre->right = root->right;root->right = root->left;root->left = nullptr;}root = root->right;return;}
};

解法二: 非递归，不使用辅助空间及全局变量
前面的递归解法实际上也使用了额外的空间，因为递归需要占用额外空间。下面的解法无需申请栈，也不用全局变量，是真正的 In-Place 解法。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {while (root != nullptr) {if (root->left != nullptr) {auto most_right = root->left; // 如果左子树不为空, 那么就先找到左子树的最右节点while (most_right->right != nullptr) most_right = most_right->right; // 找最右节点most_right->right = root->right; // 然后将跟的右孩子放到最右节点的右子树上root->right = root->left; // 这时候跟的右孩子可以释放, 因此我令左孩子放到右孩子上root->left = nullptr; // 将左孩子置为空}root = root->right; // 继续下一个节点}return;}
};

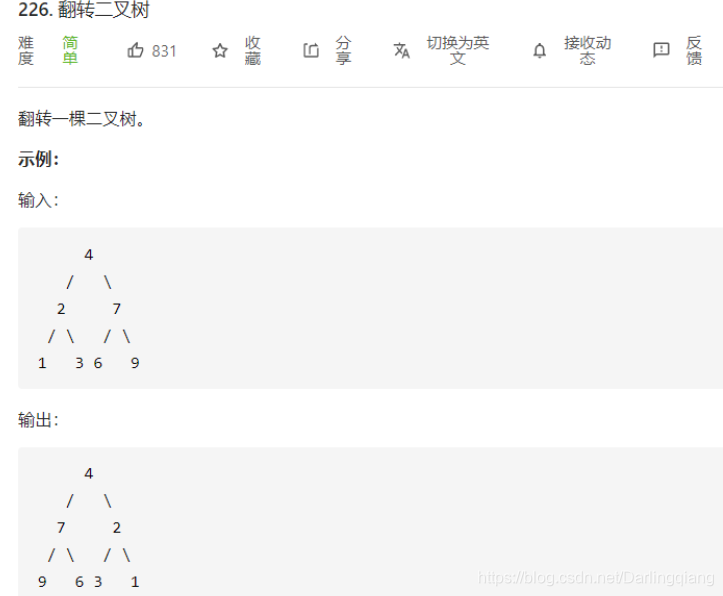
leetcode 226. 翻转二叉树

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M5Zo096g-1619446816610)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\1619309137259.png)]

//根 左 右

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(root==NULL) return root;swap(root->left,root->right);invertTree(root->left);invertTree(root->right);return root;}
};

思路与算法

这是一道很经典的二叉树问题。显然，我们从根节点开始，递归地对树进行遍历，并从叶子结点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转。

// 左 右 根

class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == nullptr) {return nullptr;}TreeNode* left = invertTree(root->left);TreeNode* right = invertTree(root->right);root->left = right;root->right = left;return root;}
};

复杂度分析

时间复杂度：O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。

空间复杂度：O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即O(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

leetcode 剑指 Offer 32 - I. 从上到下打印二叉树

BFS算法流程：

特例处理： 当树的根节点为空，则直接返回空列表 [] ；
初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
BFS 循环： 当队列 queue 为空时跳出；
出队： 队首元素出队，记为 node；
打印： 将 node对应val 添加至列表 ans尾部；
添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
返回值： 返回打印结果列表 ans即可。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
//BFS
class Solution {
public:vector<int> levelOrder(TreeNode* root){vector<int> ans;if(root == NULL) return ans;queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode* node=q.front();q.pop();ans.push_back(node->val);if(node->left) q.push(node->left);if(node->right) q.push(node->right);}return ans;}//DFS// void getResult(TreeNode *root, int k,vector<vector<int>> &ans){//     if(root == NULL) return;//     if(k == ans.size())  ans.push_back(vector<int>());//     ans[k].push_back(root->val);//     getResult(root->left, k + 1, ans);//     getResult(root->right, k + 1, ans);//     return;// }// vector<vector<int>> levelOrder(TreeNode* root) {//     vector<vector<int>> ans;//     getResult(root , 0 , ans);//     return ans;// }
};

复杂度分析：

时间复杂度 O(N） ： N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 O(N) ： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

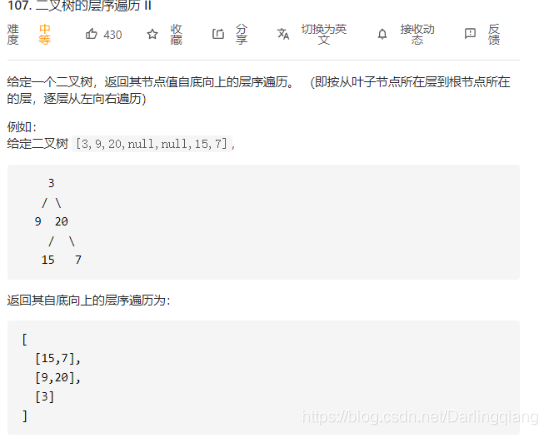
leetcode 107. 二叉树的层序遍历 II

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void getResult(TreeNode *root,int k, vector<vector<int>> &ans){if(root==NULL) return;if(k == ans.size()) ans.push_back(vector<int>());ans[k].push_back(root->val);getResult(root->left,k+1,ans);getResult(root->right,k+1,ans);return;}//前序遍历 //根 左 右    [3]，[9,20], [15,7]vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> ans;getResult(root,0,ans);for(int i=0,j=ans.size()-1;i<j;i++,j--){swap(ans[i],ans[j]);}return ans;}
};

学会二叉树的层序遍历，可以一口气撸完leetcode一下八道题目：

102.二叉树的层序遍历
107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的前序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II

102.二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

思路
我们之前讲过了三篇关于二叉树的深度优先遍历的文章：

接下来我们再来介绍二叉树的另一种遍历方式：层序遍历。

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

使用队列实现二叉树广度优先遍历，动画如下：

这样就实现了层序从左到右遍历二叉树。

代码如下：这份代码也可以作为二叉树层序遍历的模板，以后再打后面的题目就靠它了。

BFS树/图的层序遍历，或者广度优先搜索，基于queue数据结构实现

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;// 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;}
};

199.二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

思路
层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。

class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<int> result;while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (i == (size - 1)) result.push_back(node->val);// 将每一层的最后元素放入result数组中if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};

637.二叉树的层平均值

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

思路 本题就是层序遍历的时候把一层求个总和在取一个均值。

class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<double> result;while (!que.empty()) {int size = que.size();double sum = 0; // 统计每一层的和for (int i = 0; i < size; i++) { TreeNode* node = que.front();que.pop();sum += node->val;if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(sum / size); // 将每一层均值放进结果集}return result;}
};

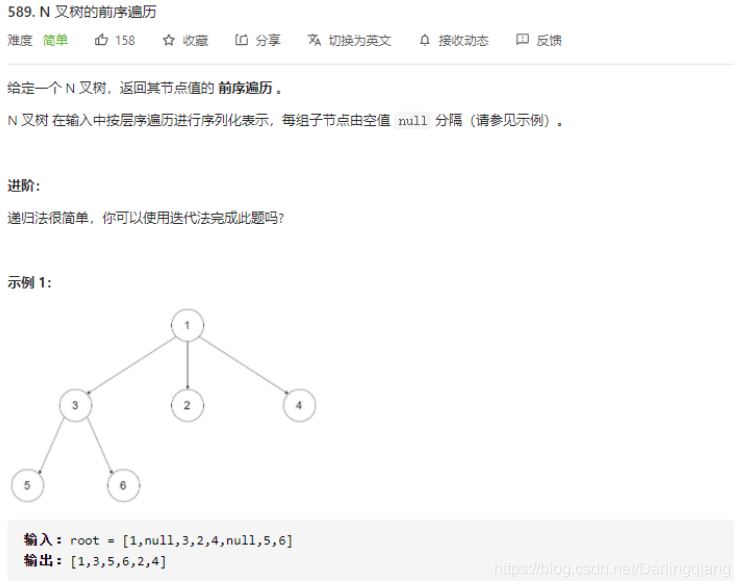
leetcode 589. N 叉树的前序遍历

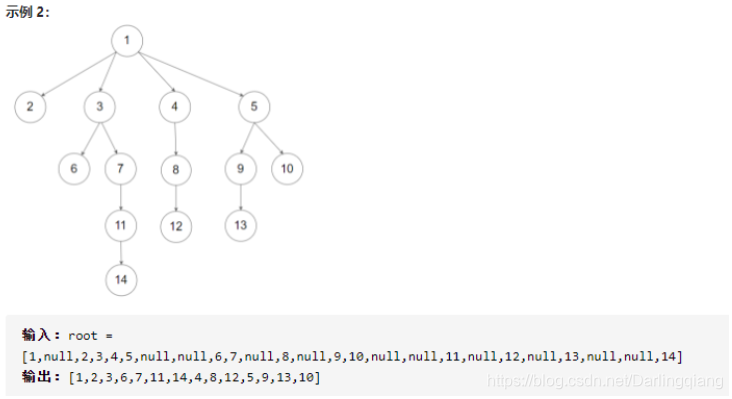
/*// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) { val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/
class Solution {
public:void __preorder(Node* root,vector<int> &ans){if(root==NULL) return ;ans.push_back(root->val);for(auto x:root->children){__preorder(x,ans);}}vector<int> preorder(Node* root) {vector<int> ans;__preorder(root,ans);return ans;}
};

树的遍历(Traversal)

如下图, 三种遍历方式, 可用同一种递归思想实现

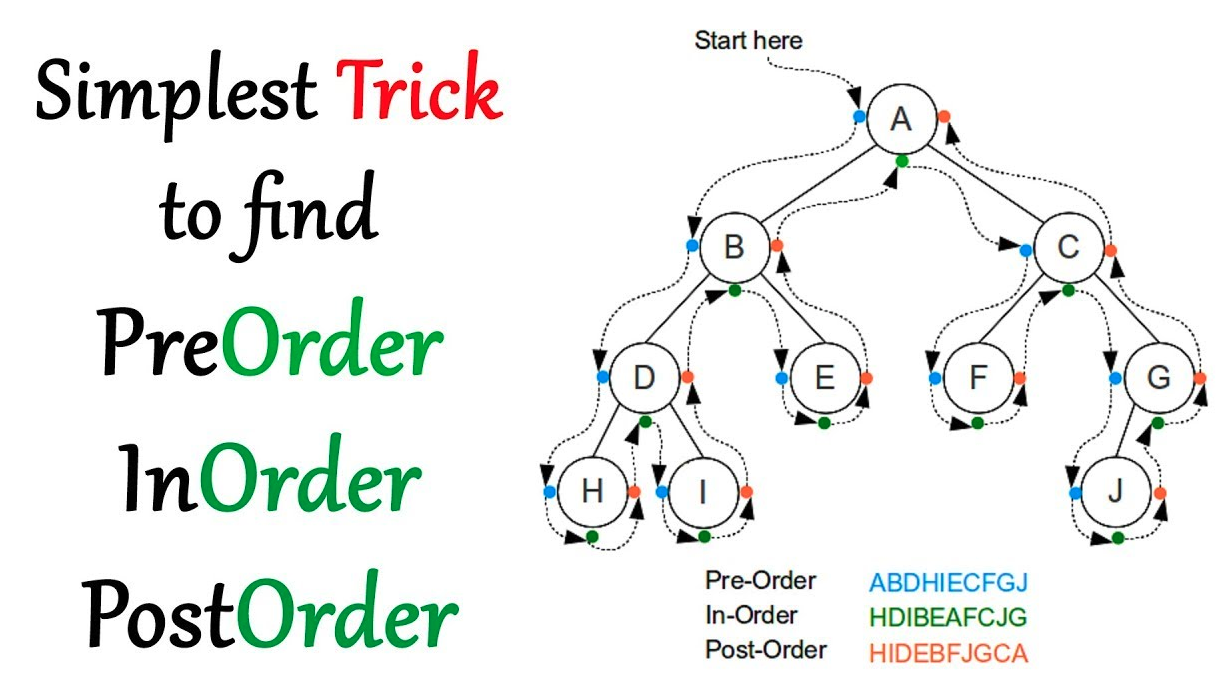
递归算法的三个要素。每次写递归，都按照这三要素来写，可以保证大家写出正确的递归算法！

确定递归函数的参数和返回值：

确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。

确定终止条件：

写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。

确定单层递归的逻辑：

确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

以下以前序遍历为例：

确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec)

确定终止条件：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

if (cur == NULL) return;

确定单层递归的逻辑：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

单层递归的逻辑就是按照中左右的顺序来处理的，这样二叉树的前序遍历，基本就写完了，在看一下完整代码：

前序遍历(preorder, 按照先访问根节点的顺序)

class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val);    // 根traversal(cur->left, vec);  // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

中序遍历：(inorder, 按照先访问顺序,左 根 右)

void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec);  // 左vec.push_back(cur->val);    // 根traversal(cur->right, vec); // 右
}

后序遍历：(lastorder, 按照先访问顺序,左 右 根 )

void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec);  // 左traversal(cur->right, vec); // 右vec.push_back(cur->val);    // 根
}

此时大家可以做一做leetcode上三道题目，分别是：

144.二叉树的前序遍历 迭代法

为什么可以用迭代法（非递归的方式）来实现二叉树的前后中序遍历呢？

我们在栈与队列：匹配问题都是栈的强项中提到了，递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

此时大家应该知道我们用栈也可以是实现二叉树的前后中序遍历了。

前序遍历（迭代法）
我们先看一下前序遍历。

前序遍历是中左右，每次先处理的是中间节点，那么先将跟节点放入栈中，然后将右孩子加入栈，再加入左孩子。

为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。

动画如下：

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();                       // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right);           // 右（空节点不入栈）if (node->left) st.push(node->left);             // 左（空节点不入栈）}return result;}
};

94.二叉树的中序遍历 中序遍历（迭代法）

为了解释清楚，我说明一下 刚刚在迭代的过程中，其实我们有两个操作：

处理：将元素放进result数组中
访问：遍历节点
分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序***是不一致的。****

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

动画如下：

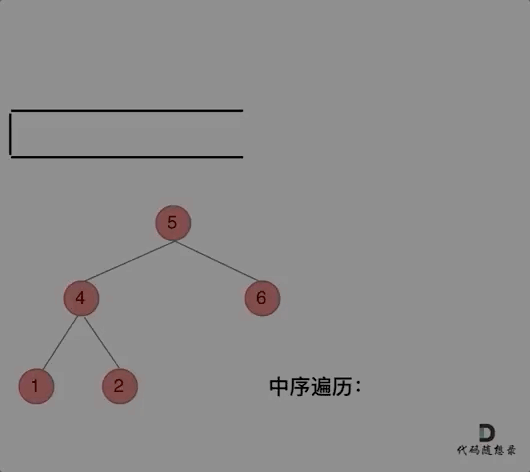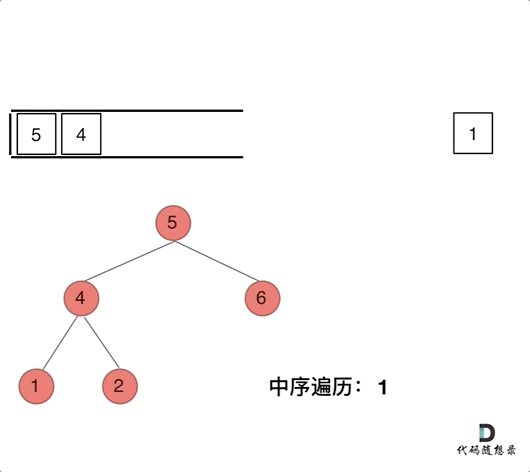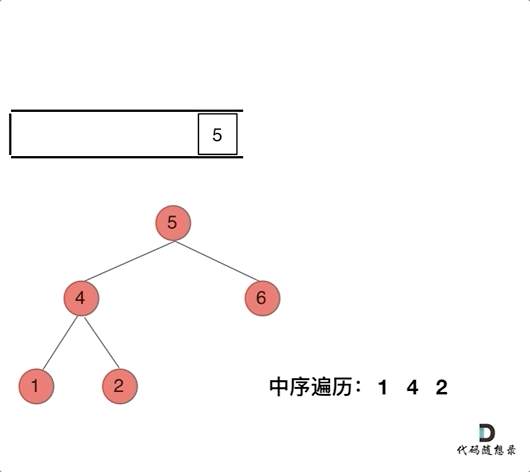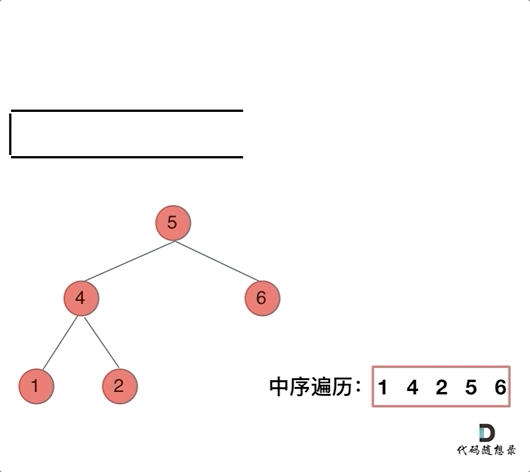
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点，访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left;                // 左} else {cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）st.pop();result.push_back(cur->val);     // 中cur = cur->right;               // 右}}return result;}
};

145.二叉树的后序遍历（迭代法）

再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};

此时我们实现了前后中遍历的三种迭代法，是不是发现迭代法实现的先中后序，其实风格也不是那么统一，除了先序和后序，有关联，中序完全就是另一个风格了，一会用栈遍历，一会又用指针来遍历。

二叉树前中后迭代方式统一写法

之后我们发现迭代法实现的先中后序，其实风格也不是那么统一，除了先序和后序，有关联，中序完全就是另一个风格了，一会用栈遍历，一会又用指针来遍历。

实践过的同学，也会发现使用迭代法实现先中后序遍历，很难写出统一的代码，不像是递归法，实现了其中的一种遍历方式，其他两种只要稍稍改一下节点顺序就可以了。

其实针对三种遍历方式，使用迭代法是可以写出统一风格的代码！

重头戏来了，接下来介绍一下统一写法。

那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。

如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。

迭代法中序遍历
中序遍历代码如下：（详细注释）

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）st.push(node);                          // 添加中节点st.push(NULL); // 中节点访问过，但是还没有处理，加入空节点做为标记。if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）} else { // 只有遇到空节点的时候，才将下一个节点放进结果集st.pop();           // 将空节点弹出node = st.top();    // 重新取出栈中元素st.pop();result.push_back(node->val); // 加入到结果集}}return result;}
};

迭代法前序遍历
迭代法前序遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right);  // 右if (node->left) st.push(node->left);    // 左st.push(node);                          // 中st.push(NULL);} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}
};

迭代法后序遍历
后续遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node);                          // 中st.push(NULL);if (node->right) st.push(node->right);  // 右if (node->left) st.push(node->left);    // 左} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}};

N叉树的前序遍历

和二叉树的道理是一样的，直接给出代码了

递归C++代码

class Solution {
private:vector<int> result;void traversal (Node* root) {if (root == NULL) return;result.push_back(root->val);for (int i = 0; i < root->children.size(); i++) {traversal(root->children[i]);}}public:vector<int> preorder(Node* root) {result.clear();traversal(root);return result;}
};

迭代法C++代码

class Solution {public:vector<int> preorder(Node* root) {vector<int> result;if (root == NULL) return result;stack<Node*> st;st.push(root);while (!st.empty()) {Node* node = st.top();st.pop();result.push_back(node->val);// 注意要倒叙，这样才能达到前序（中左右）的效果for (int i = node->children.size() - 1; i >= 0; i--) {if (node->children[i] != NULL) {st.push(node->children[i]);}}}return result;}
};

N叉树的后序遍历

递归C++代码o

class Solution {
private:vector<int> result;void traversal (Node* root) {if (root == NULL) return;for (int i = 0; i < root->children.size(); i++) { // 子孩子traversal(root->children[i]);}result.push_back(root->val); // 中}public:vector<int> postorder(Node* root) {result.clear();traversal(root);return result;}};

迭代法C++代码

class Solution {
public:vector<int> postorder(Node* root) {vector<int> result;if (root == NULL) return result;stack<Node*> st;st.push(root);while (!st.empty()) {Node* node = st.top();st.pop();result.push_back(node->val);for (int i = 0; i < node->children.size(); i++) { // 相对于前序遍历，这里反过来if (node->children[i] != NULL) {st.push(node->children[i]);}}}reverse(result.begin(), result.end()); // 反转数组return result;}
};

总结

对于二叉树，我们写出了前中后序的递归，以及对应的迭代法，然后分析出为什么写出统一风格的迭代法比较难。

进而给出了前中后序统一风格的迭代法代码。

我们可以写出了统一风格的迭代法，不用在纠结于前序写出来了，中序写不出来的情况了。

但是统一风格的迭代法并不好理解，而且想在面试直接写出来还有难度的。

所以大家根据自己的个人喜好，对于二叉树的前中后序遍历，选择一种自己容易理解的递归和迭代法。

最后在给出N叉树的前后序遍历的递归与迭代。理解了以上二叉树的遍历方式，N叉树就容易很多了，都是一个套路。

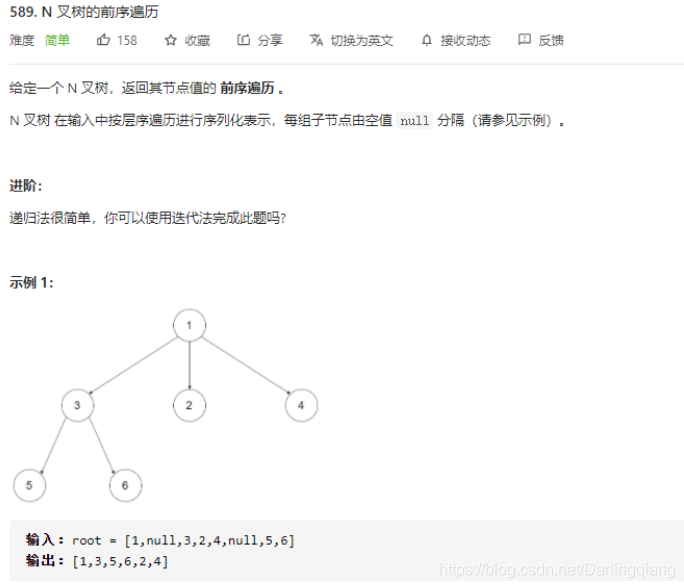
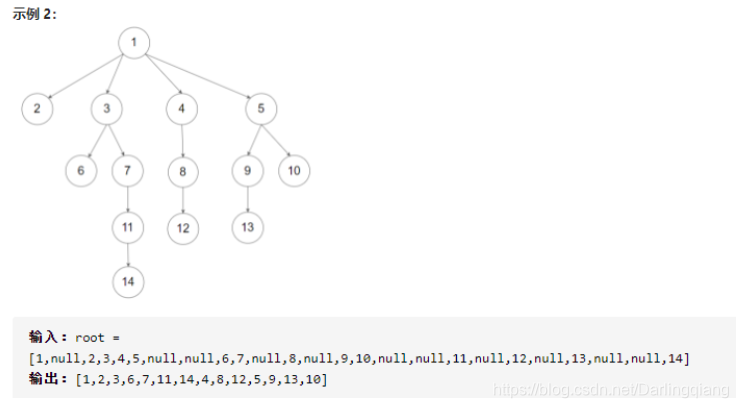
leetcode 589. N 叉树的前序遍历

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) { val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/
class Solution {
public:void __preorder(Node* root,vector<int> &ans){if(root==NULL) return ;ans.push_back(root->val);for(auto x:root->children){__preorder(x,ans);}}vector<int> preorder(Node* root) {vector<int> ans;__preorder(root,ans);return ans;}
};

429. N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

返回其层序遍历:

[
[1],
[3,2,4],
[5,6]
]

思路：这道题依旧是模板题**，只不过一个节点有多个孩子了

class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) { Node* node = que.front();que.pop();vec.push_back(node->val);for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列if (node->children[i]) que.push(node->children[i]);}}result.push_back(vec);}return result;}
};

515.在每个树行中找最大值

您需要在二叉树的每一行中找到最大的值。

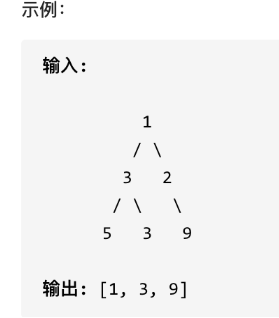
思路：层序遍历，取每一层的最大值

class Solution {
public:vector<int> largestValues(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<int> result;while (!que.empty()) {int size = que.size();int maxValue = INT_MIN; // 取每一层的最大值for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();maxValue = node->val > maxValue ? node->val : maxValue;if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(maxValue); // 把最大值放进数组}return result;}
};

116.填充每个节点的下一个右侧节点指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

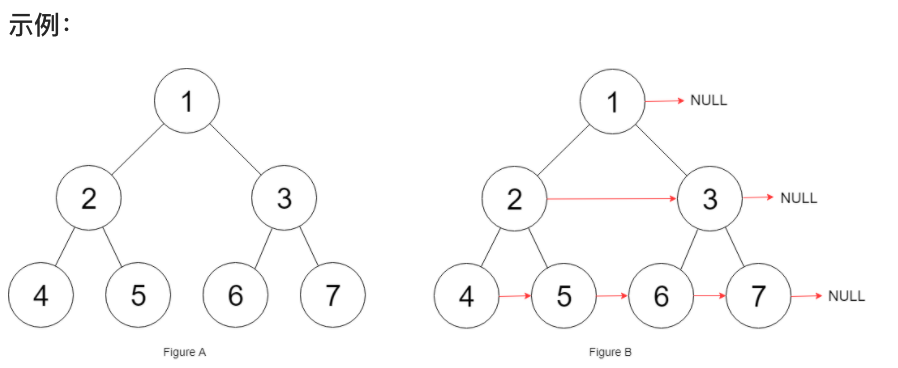
思路：本题依然是层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了

class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if (root != NULL) que.push(root);while (!que.empty()) {int size = que.size();vector<int> vec;Node* nodePre;Node* node;for (int i = 0; i < size; i++) {if (i == 0) {nodePre = que.front(); // 取出一层的头结点que.pop();node = nodePre;} else {node = que.front();que.pop();nodePre->next = node; // 本层前一个节点next指向本节点nodePre = nodePre->next;}if (node->left) que.push(node->left);if (node->right) que.push(node->right);}nodePre->next = NULL; // 本层最后一个节点指向NULL}return root;}
};

117.填充每个节点的下一个右侧节点指针II

思路：这道题目说是二叉树，但116题（上题）目说是完整二叉树，其实没有任何差别，一样的代码一样的逻辑一样的味道

class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if (root != NULL) que.push(root);while (!que.empty()) {int size = que.size();vector<int> vec;Node* nodePre;Node* node;for (int i = 0; i < size; i++) {if (i == 0) {nodePre = que.front(); // 取出一层的头结点que.pop();node = nodePre;} else {node = que.front();que.pop();nodePre->next = node; // 本层前一个节点next指向本节点nodePre = nodePre->next;}if (node->left) que.push(node->left);if (node->right) que.push(node->right);}nodePre->next = NULL; // 本层最后一个节点指向NULL}return root;}
};

总结

二叉树的层序遍历，就是图论中的广度优先搜索在二叉树中的应用，需要借助队列来实现（此时是不是又发现队列的应用了）。（虽然不能一口气打十个，打八个也还行。）

leetcode 103. 二叉树的锯齿形层序遍历

1. 先进行层序遍历，将遍历结果存储到二维数组中，
2. 依次遍历存储所有结果，
3. 若对应行数为偶数，倒序该数组，反之，正常存储。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void getResult(TreeNode* root,int k,vector<vector<int>> &ans){if(root==NULL) return;if(k==ans.size()) ans.push_back(vector<int>());ans[k].push_back(root->val);getResult(root->left,k+1,ans);getResult(root->right,k+1,ans);return;}void reverse(vector<int> &ans){for(int i=0,j=ans.size()-1;i<j;i++,j--){swap(ans[i],ans[j]);}return;}vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ans;getResult(root,0,ans);for(int i=1;i<ans.size();i+=2){reverse(ans[i]);}return ans;}
};

leetcode 110. 平衡二叉树

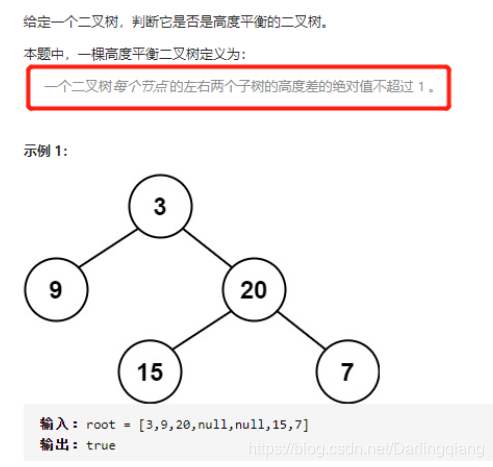
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int getHeight(TreeNode* root){if(root==NULL) return 0;int l=getHeight(root->left);//递归定义，当树不平衡时候，返回负值int r=getHeight(root->right);if(l<0||r<0) return -2;  //不平衡返回负值-2if(abs(l-r)>1) return -2;//平衡>=0return max(l,r)+1;}bool isBalanced(TreeNode* root) {return getHeight(root)>=0;}
};

讨论：递归函数的意义？ 可以表示树高 可表示树平衡。。。

leetcode 112. 路径总和

方法一：深度优先搜索递归

注意到本题的要求是，询问是否有从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和。核心思想是对树进行一次遍历，在遍历时记录从根节点到当前节点的路径和，以防止重复计算。

需要特别注意的是，给定的 root 可能为空

思路及算法

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root==NULL) return false;if(root->left == NULL && root->right ==NULL) return root->val==targetSum;if(root->left  && hasPathSum(root->left, targetSum- root->val)) return true;//左节点不为空，返回该节点的值与if(root->right && hasPathSum(root->right,targetSum- root->val)) return true;return false;}
};

复杂度分析

时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。

空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log N)。

‘’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’’

方法二：广度优先搜索

思路及算法

首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。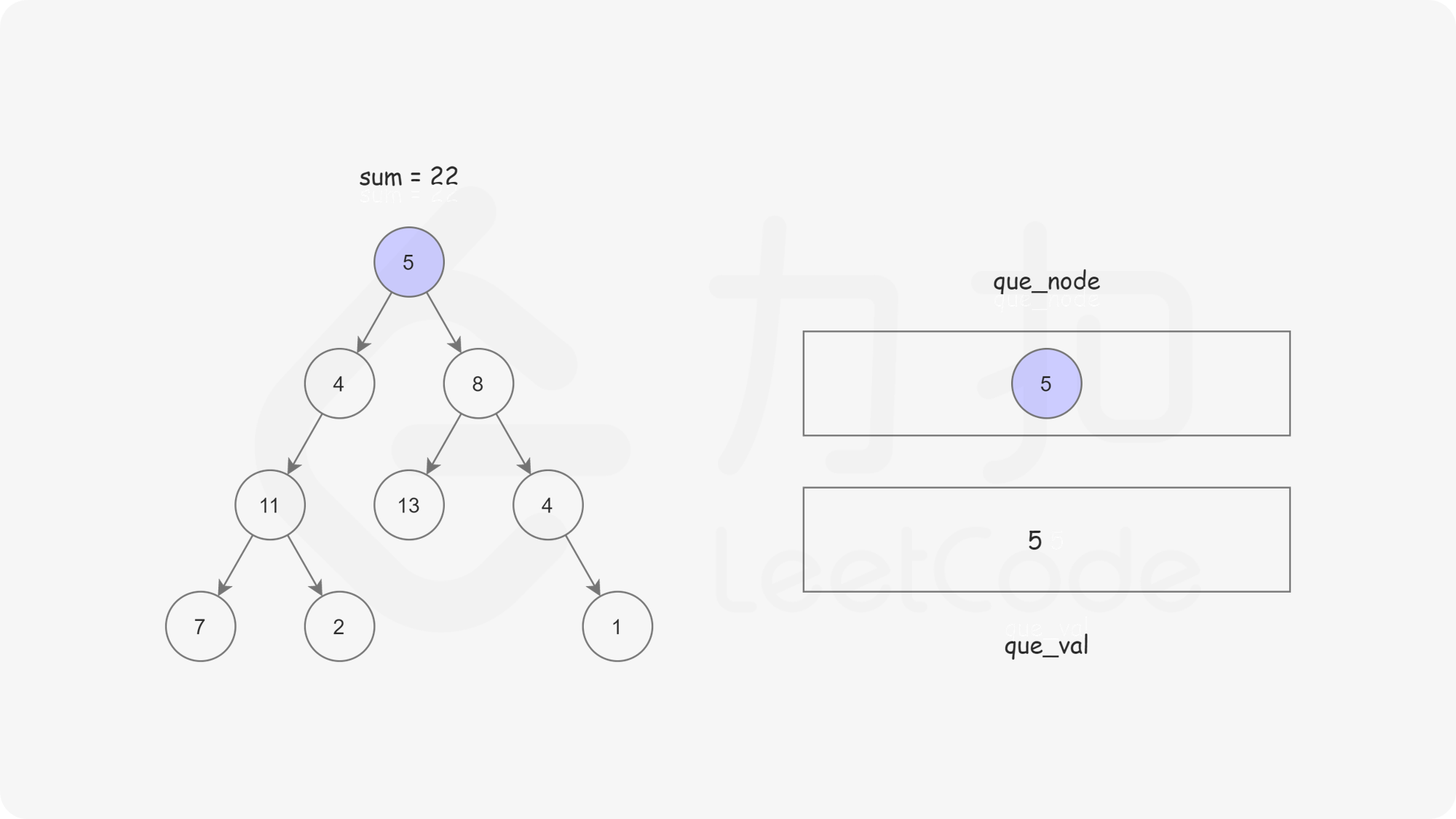

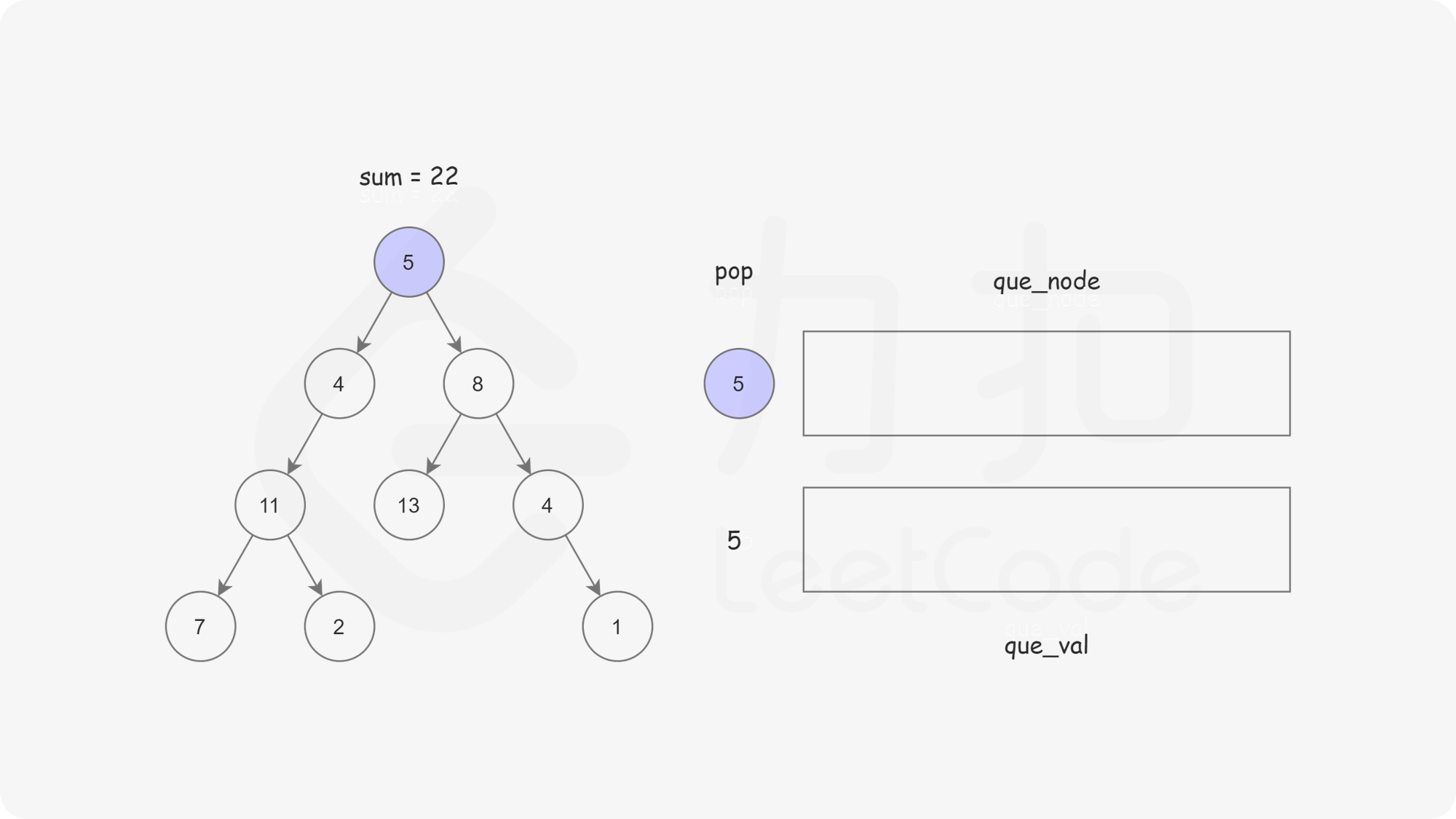
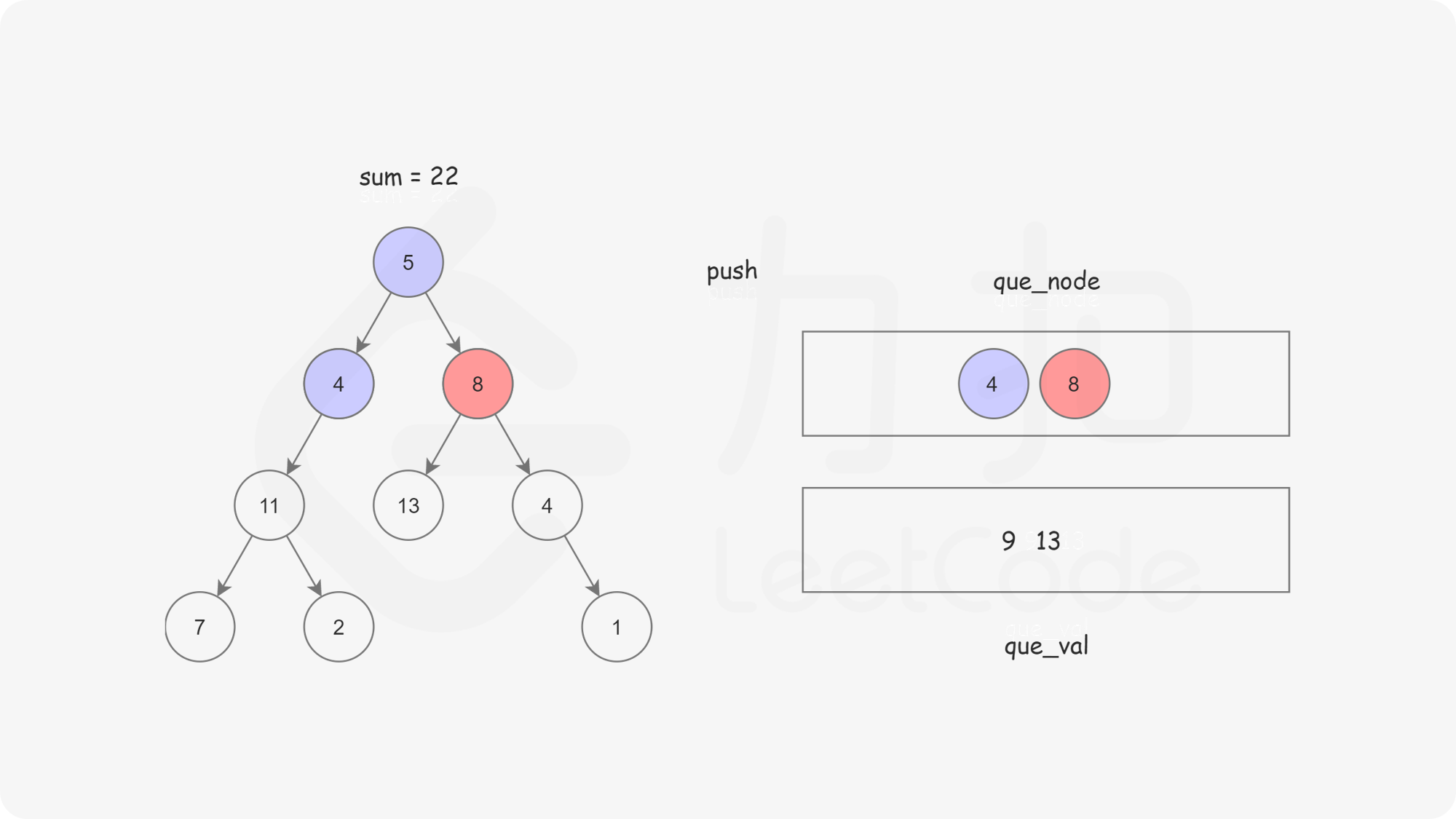
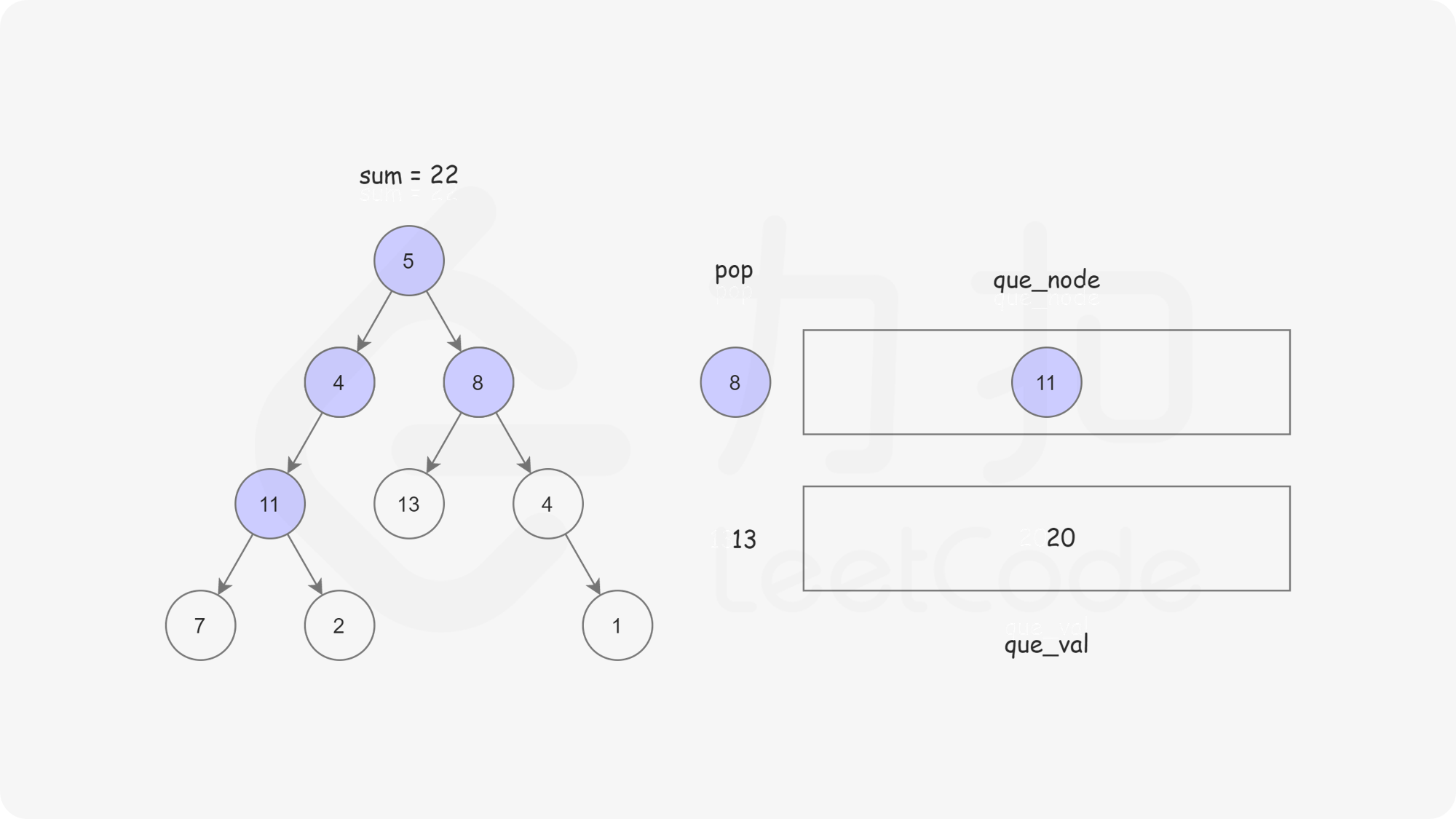
  bool hasPathSum(TreeNode* root, int targetSum) {if(root==NULL) return false;queue<TreeNode*> node;queue<int> val;node.push(root);val.push(root->val);while(!node.empty()){TreeNode* temp_node=node.front();int temp_val =val.front();node.pop();val.pop();if(temp_node->left == NULL && temp_node->right == NULL){if(temp_val == targetSum){return true;}continue;}if (temp_node->left != NULL){node.push(temp_node->left);val.push(temp_node->left->val + temp_val);}if (temp_node->right != NULL){node.push(temp_node->right);val.push(temp_node->right->val +temp_val);}}return false;}

复杂度分析

时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。

空间复杂度：O(N)，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

方法三：栈模拟递归（回溯）

如果使用栈模拟递归的话，那么如果做回溯呢？

此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

C++就我们用pair结构来存放这个栈里的元素。

定义为：pair<TreeNode*, int> pair<节点指针，路径数值> ， 这个为栈里的一个元素。

如下代码是使用栈模拟的前序遍历，如下： 根左右，栈中顺序，相反

 bool hasPathSum(TreeNode* root, int sum) {if(root ==NULL) return false;// 栈里要放的是pair<节点指针，路径数值>stack<pair<TreeNode*,int>> node;node.push(pair<TreeNode*,int>(root,root->val));//初始化while( !node.empty()){pair<TreeNode*,int> temp=node.top();node.pop();//如果当前节点为叶子节点，p判断该节点的路径数就等于sum，满足 返回trueif(!temp.first->left &&!temp.first->right&& sum == temp.second) return true;// 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来if(temp.first->right){int a = temp.first->right->val + temp.second;node.push(pair<TreeNode*,int>(temp.first->right,a));}// 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来if(temp.first->left){int b = temp.first->left->val + temp.second;node.push(pair<TreeNode*,int>(temp.first->left,b));}}wsx  return false;}

leetcode 105. 从前序与中序遍历序列构造二叉树

递归的解法 1 找根位置 2 递归建立左子树 3递归建立右子树

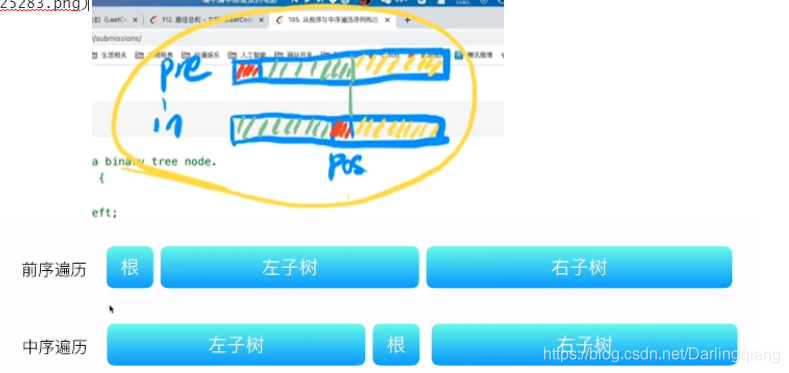
我们知道前序遍历的第一个元素肯定是根节点，那么前序遍历的第一个节点在中序位置之前的都是根节点的左子节点，之后的都是根节点的右子节点，我们来简单画个图看一下

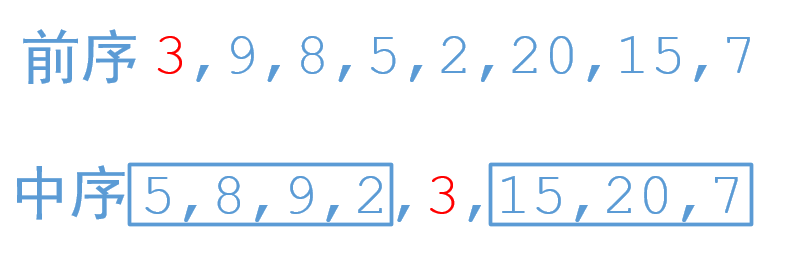
这里是随便举个例子，我们看到前序遍历的3肯定是根节点，那么在中序遍历中，3前面的都是3左子节点的值，3后面的都是3右子节点的值，他真正的结构是这样的

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.size()==0) return NULL;int pos=0;while(inorder[pos]!=preorder[0])  ++pos;vector<int> l_pre,l_in,r_pre,r_in;for(int i=0;i<pos;i++){l_pre.push_back(preorder[i+1]);l_in.push_back(inorder[i]);}for(int i=pos+1;i<preorder.size();i++){r_pre.push_back(preorder[i]);r_in.push_back(inorder[i]);}TreeNode *root=new TreeNode(preorder[0]);root->left=buildTree(l_pre,l_in);root->right=buildTree(r_pre,r_in);return root;}

2.使用指针解决

我们只需要使用3个指针即可。一个是preStart，他表示的是前序遍历开始的位置，一个是inStart，他表示的是中序遍历开始的位置。一个是inEnd，他表示的是中序遍历结束的位置，我们主要是对中序遍历的数组进行拆解，下面就以下面的这棵树来画个图分析下

他的前序遍历是：[3,9,8,5,2,20,15,7]

他的中序遍历是：[5,8,9,2,3,15,20,7]

这里只要找到了前序遍历的结点在中序遍历的位置，我们就可以把中序遍历数组分解为两部分了。如果index是前序遍历的某个值在中序遍历数组中的索引，以index为根节点划分的话，那么中序遍历中

[0，index-1]就是根节点左子树的所有节点，

[index+1，inorder.length-1]就是根节点右子树的所有节点。

中序遍历好划分，那么前序遍历呢，如果是左子树：

preStart=index+1；

如果是右子树就稍微麻烦点，

preStart=preStart+(index-instart+1)；

preStart是当前节点比如m先序遍历开始的位置，index-instart+1就是当前节点m左子树的数量加上当前节点的数量，所以preStart+(index-instart+1)就是当前节点m右子树前序遍历开始的位置，我们来看下完整代码

public TreeNode buildTree(int[] preorder, int[] inorder) {return helper(0, 0, inorder.length - 1, preorder, inorder);
}public TreeNode helper(int preStart, int inStart, int inEnd, int[] preorder, int[] inorder) {if (preStart > preorder.length - 1 || inStart > inEnd) {return null;}//创建结点TreeNode root = new TreeNode(preorder[preStart]);int index = 0;//找到当前节点root在中序遍历中的位置，然后再把数组分两半for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == root.val) {index = i;break;}}root.left = helper(preStart + 1, inStart, index - 1, preorder, inorder);root.right = helper(preStart + index - inStart + 1, index + 1, inEnd, preorder, inorder);return root;
}

3，使用栈解决
如果使用栈来解决首先要搞懂一个知识点，就是前序遍历挨着的两个值比如m和n，他们会有下面两种情况之一的关系。

1，n是m左子树节点的值。

2，n是m右子树节点的值或者是m某个祖先节点的右节点的值。

对于第一个知识点我们很容易理解，如果m的左子树不为空，那么n就是m左子树节点的值。

对于第二个问题，如果一个结点没有左子树只有右子树，那么n就是m右子树节点的值，如果一个结点既没有左子树也没有右子树，那么n就是m某个祖先节点的右节点，我们只要找到这个祖先节点就好办了。

搞懂了这点，代码就很容易写了，下面看下完整代码

public TreeNode buildTree(int[] preorder, int[] inorder) {if (preorder.length == 0)return null;Stack<TreeNode> s = new Stack<>();//前序的第一个其实就是根节点TreeNode root = new TreeNode(preorder[0]);TreeNode cur = root;for (int i = 1, j = 0; i < preorder.length; i++) {//第一种情况if (cur.val != inorder[j]) {cur.left = new TreeNode(preorder[i]);s.push(cur);cur = cur.left;} else {//第二种情况j++;//找到合适的cur，然后确定他的右节点while (!s.empty() && s.peek().val == inorder[j]) {cur = s.pop();j++;}//给cur添加右节点cur = cur.right = new TreeNode(preorder[i]);}}return root;
}

leetcode 222. 完全二叉树的节点个数

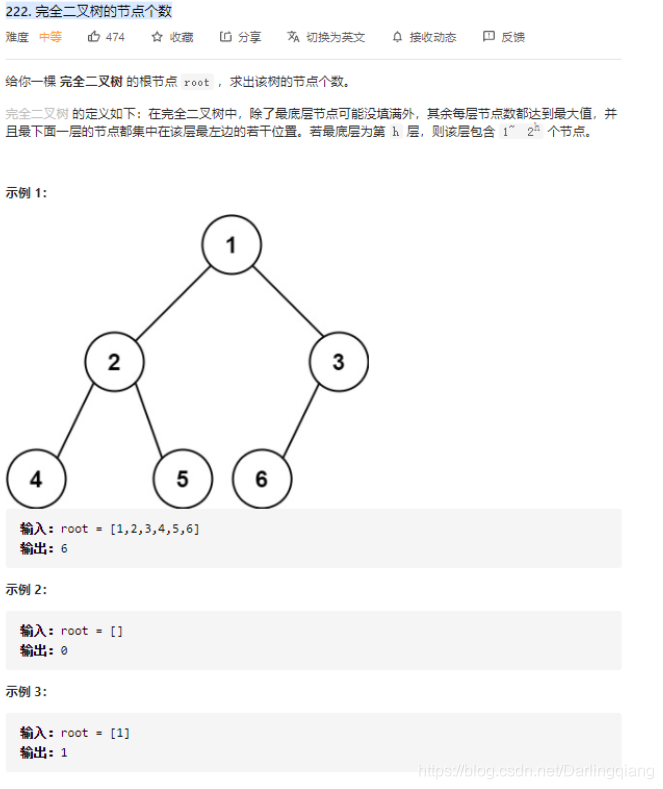
方法一：适合所有类型的树的节点计算

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int countNodes(TreeNode* root) {if(root==NULL) return 0;return countNodes(root->left)+countNodes(root->right)+1;}
};

方法二：dfs

满二叉树
定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
也就是说，如果一个二叉树的层数为K（从1开始的），每一层的节点个数为2^(k-1) ，且结点总数是(2^k)-1.
代码:k为子树的层数，那么子树的节点总数(1<<k)-1;加减运算优先级高于位移运算符

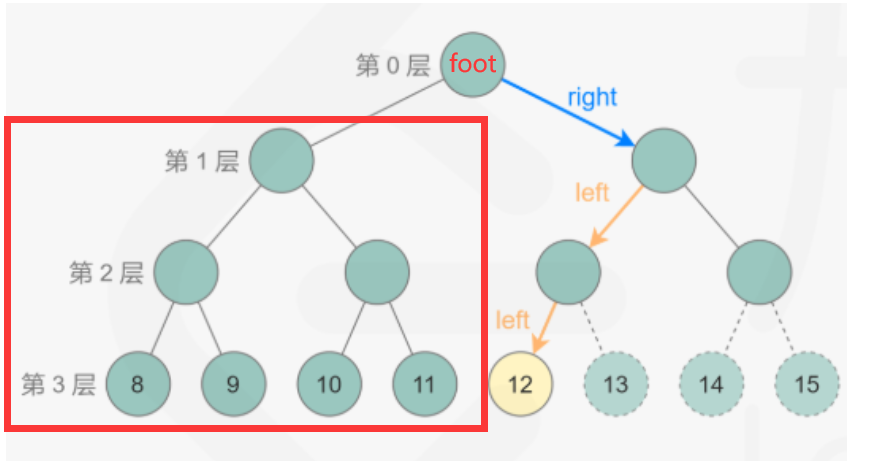
完全二叉树
定义：它是一棵空树或者它的叶子节点只出在最后两层，若最后一层不满则叶子节点只在最左侧。

1.如果根节点的左子树深度等于右子树深度，则说明左子树为满二叉树。

//(1<<left_level)注意括号，子树节点数目为(1<<left_level)-1，再+1（root节点）
if(left_level == right_level){return (1<<left_level) + count(root->right);
} 

2. 如果根节点的左子树深度大于右子树深度，则说明右子树为满二叉树

if(left_level != right_level) {return count(root->left) + (1<<right_level);
}

三种做法的代码

1.暴力求解，深度递归dfs

class Solution {
public:int countNodes(TreeNode* root) {return root == NULL? 0:countNodes(root->left)+countNodes(root->right)+1;}
};

2.运用完全二叉树的性质（和满二叉树结合）

class Solution {
public://计算子树层数int countlevel(TreeNode* root){int level = 0;while(root!=NULL){root = root->left;level++;}return level;}int countNodes(TreeNode* root) {if(root==NULL)return 0;int leftlevel = countlevel(root->left);int rightlevel = 0;int count = 0;while(root){rightlevel = countlevel(root->right);//左边子树是满二叉树if(leftlevel == rightlevel){count += (1<<leftlevel);root = root->right;}//右边子树是满二叉树else{count += (1<<rightlevel);root = root->left;}leftlevel--;    }return count;}
};

1. 运用编码和位运算

• 通过二分查找，寻找叶子节点是否存在

class Solution {
public: bool exit(int index,TreeNode* root,int level){//level=3,k子树的层数对应 100，按位取&计算index，往左还是往右int k = 1<<(level-1);while(root && k>0){//1右移if(index & k){root = root->right;}//0右移else{root = root->left;}k>>=1;}return root!=NULL;}int countNodes(TreeNode* root) {if(root==NULL)return 0;int level = -1;TreeNode* root1 = root;while(root){root=root->left;level++;}int low = (1<<level);int high = (1<<(level+1))-1;int mid = 0;while(low < high){//mid存在，往右侧找//因为high = mid-1，缩小的右边;需要向上取整mid = (high - low + 1) / 2 + low;// mid = low+((high-low+1)>>1);if(exit(mid,root1,level)){low = mid;}//mid不存在，左侧找else{high = mid-1;}}return low;}
};

3.方法三：二分查找 + 位运算

对于任意二叉树，都可以通过广度优先搜索或深度优先搜索计算节点个数，时间复杂度和空间复杂度都是 O(n)，其中 n 是二叉树的节点个数。这道题规定了给出的是完全二叉树，因此可以利用完全二叉树的特性计算节点个数。

规定根节点位于第 00 层，完全二叉树的最大层数为 h。根据完全二叉树的特性可知，完全二叉树的最左边的节点一定位于最底层，因此从根节点出发，每次访问左子节点，直到遇到叶子节点，该叶子节点即为完全二叉树的最左边的节点，经过的路径长度即为最大层数h。

当 0≤i<h 时，第 i层包含2^i ，最底层包含的节点数最少为 1，最多为 2^h 。

当最底层包含 1个节点时，完全二叉树的节点个数是
$$\sum _{i=0}^{h-1}{2}^i+1=2^h$$
当最底层包含 2^h个节点时，完全二叉树的节点个数是
$$\sum _{i=0}^h{2}^i=2^{h+1}-1$$
因此对于最大层数为 h的完全二叉树，节点个数一定在 [2^h,2{h+1}-1][2 h ,2 h+1 −1] 的范围内，可以在该范围内通过二分查找的方式得到完全二叉树的节点个数。

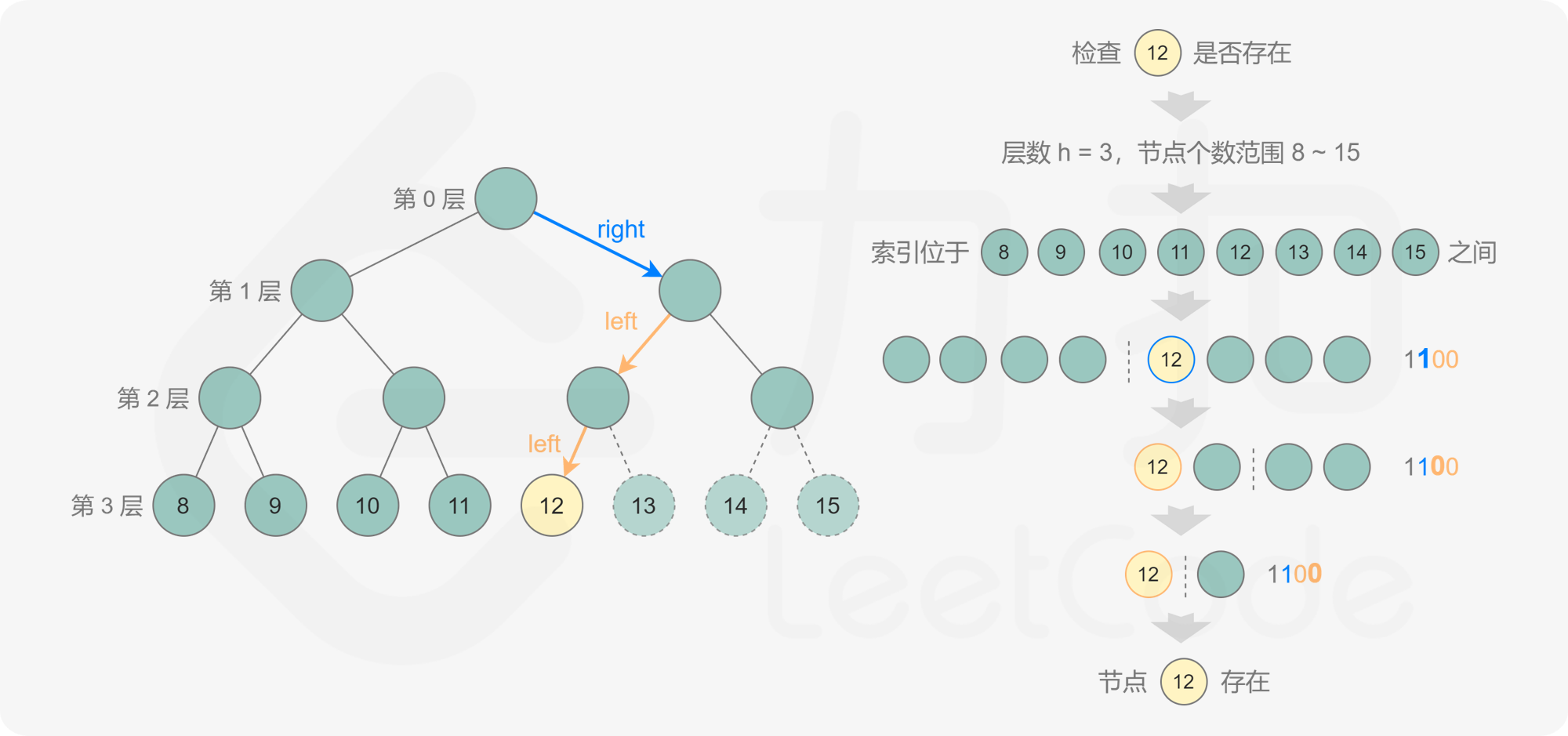
具体做法是，根据节点个数范围的上下界得到当前需要判断的节点个数 k，如果第 k个节点存在，则节点个数一定大于或等于 k，如果第 k个节点不存在，则节点个数一定小于 k，由此可以将查找的范围缩小一半，直到得到节点个数。

如何判断第 k 个节点是否存在呢？如果第 k 个节点位于第 h 层，则 k 的二进制表示包含 h+1 位，其中最高位是 1，其余各位从高到低表示从根节点到第 k个节点的路径，0表示移动到左子节点，1表示移动到右子节点。通过位运算得到第 k 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 k 个节点是否存在。

class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) {return 0;}int level = 0;TreeNode* node = root;while (node->left != nullptr) {level++;node = node->left;}int low = 1 << level, high = (1 << (level + 1)) - 1;while (low < high) {int mid = (high - low + 1) / 2 + low;if (exists(root, level, mid)) {low = mid;} else {high = mid - 1;}}return low;}bool exists(TreeNode* root, int level, int k) {int bits = 1 << (level - 1);TreeNode* node = root;while (node != nullptr && bits > 0) {if (!(bits & k)) {node = node->left;} else {node = node->right;}bits >>= 1;}return node != nullptr;}
};

  1            h = 0/ \2   3          h = 1/ \  /
4  5 6           h = 2

现在这个树中的值都是节点的编号，最底下的一层的编号是[2^h ，2^h - 1]，现在h = 2，也就是4, 5, 6, 7。
4, 5, 6, 7对应二进制分别为 100 101 110 111 不看最左边的1，从第二位开始，0表示向左，1表示向右，正好可以表示这个节点相对于根节点的位置。
比如4的 00 就表示从根节点 向左 再向左。6的 10 就表示从根节点 向右 再向左那么想访问最后一层的节点就可以从节点的编号的二进制入手。从第二位开始的二进制位表示了最后一层的节点相对于根节点的位置。
那么就需要一个bits = 2^(h - 1) 这里就是2，对应二进制为010。这样就可以从第二位开始判断。
比如看5这个节点存不存在，先通过位运算找到编号为5的节点相对于根节点的位置。010 & 101 发现第二位是0，说明从根节点开始，第一步向左走。
之后将bit右移一位，变成001。001 & 101 发现第三位是1，那么第二步向右走。
最后bit为0，说明已经找到编号为5的这个节点相对于根节点的位置，看这个节点是不是空，不是说明存在，exist返回真
编号为5的节点存在，说明总节点数量一定大于等于5。所以二分那里low = mid再比如看7存不存在，010 & 111 第二位为1，第一部从根节点向右；001 & 111 第三位也为1，第二步继续向右。
然后判断当前节点是不是null，发现是null，exist返回假。
编号为7的节点不存在，说明总节点数量一定小于7。所以high = mid - 1

leetcode 剑指 Offer 54. 二叉搜索树的第k大节点

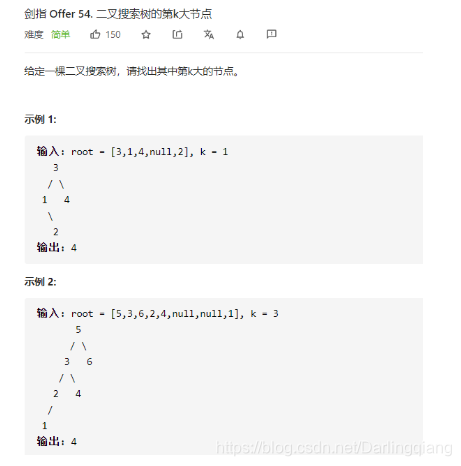
方法一：递归的方式

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int getCount(TreeNode *root){if(root==NULL) return 0;return getCount(root->left)+getCount(root->right)+1;}int kthLargest(TreeNode* root, int k) {int cnt_r=getCount(root->right);if(k<=cnt_r) return kthLargest(root->right,k);if(k==cnt_r+1) return root->val;return kthLargest(root->left,k-cnt_r-1);}
};

方法二：先求前序遍历数组，在根据数组求第k大的值

 void in_order(TreeNode *root,vector<int> &ans){if(root == NULL) return;in_order(root->left,ans);ans.push_back(root->val);in_order(root->right,ans);return;}int kthLargest(TreeNode* root, int k) {vector<int> ans;in_order(root,ans);return ans[ans.size() -k];}

本文解法基于此性质：二叉搜索树的中序遍历为 递增序列 。

根据以上性质，易得二叉搜索树的 中序遍历倒序 为 递减序列 。
因此，求 “二叉搜索树第 k大的节点” 可转化为求 “此树的中序遍历倒序的第 k 个节点”。

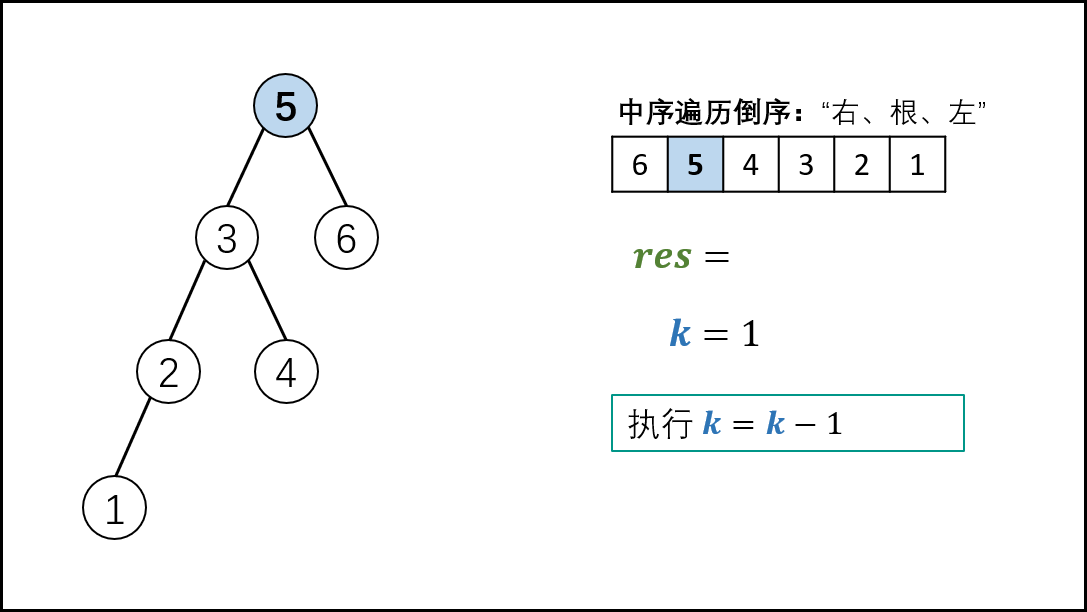
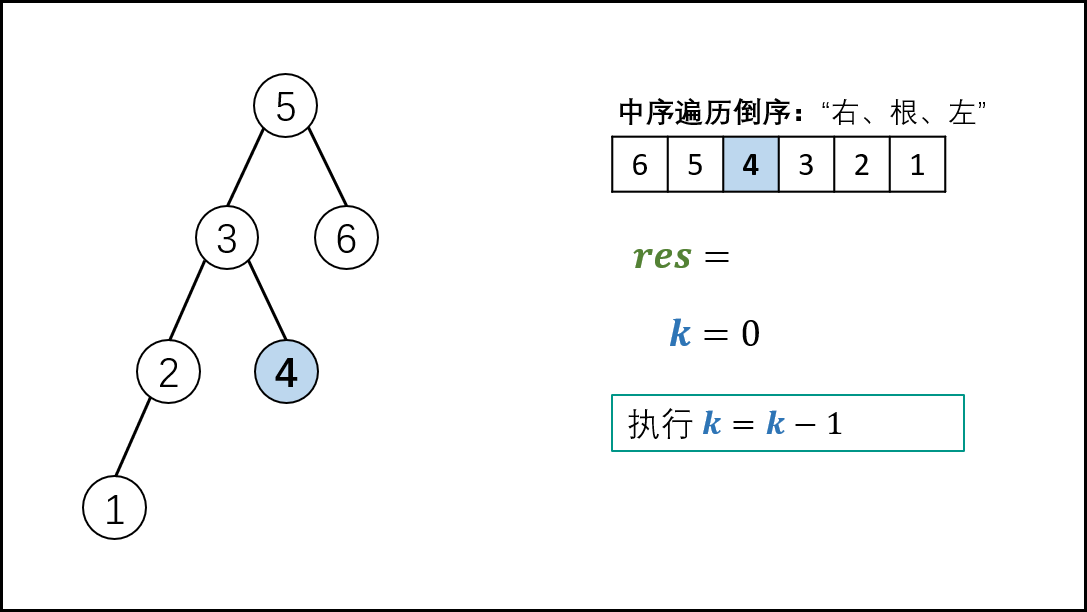
中序遍历 为 “左、根、右” 顺序，递归法代码如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DTqA705W-1619446816627)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\1619020119201.png)]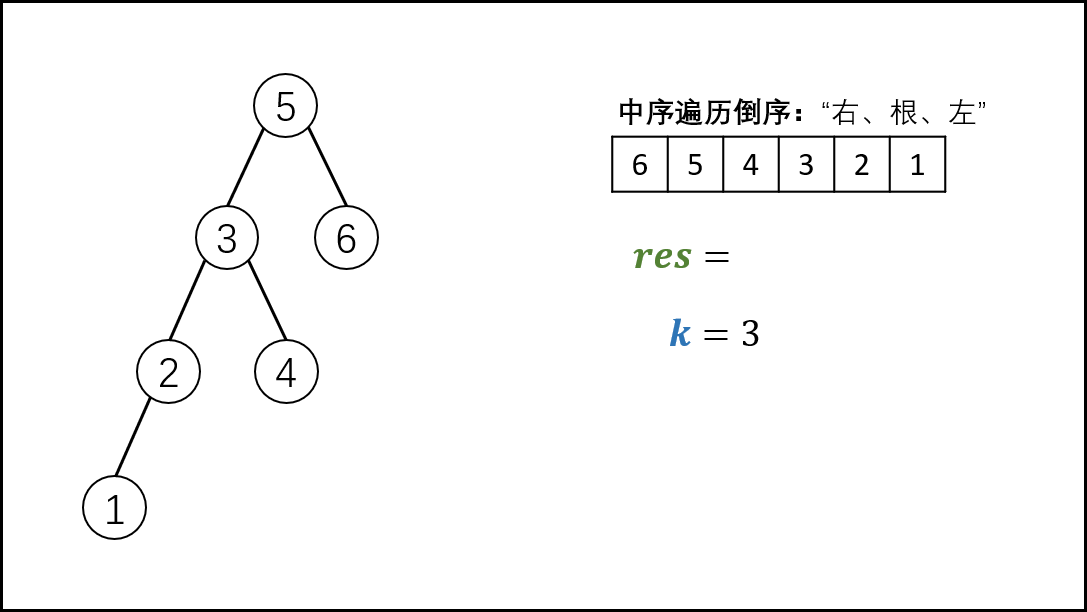

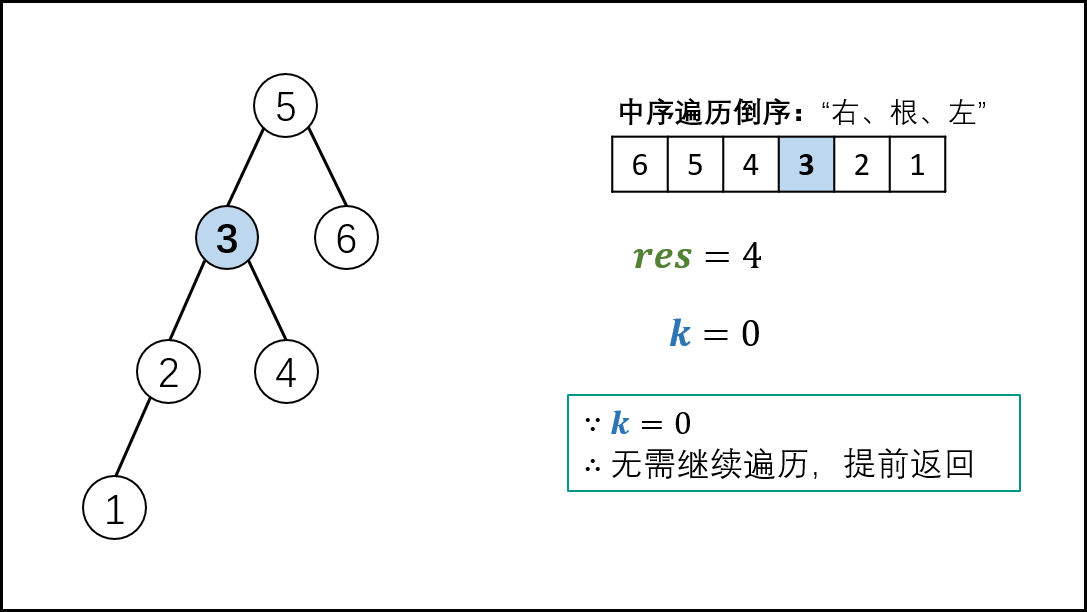
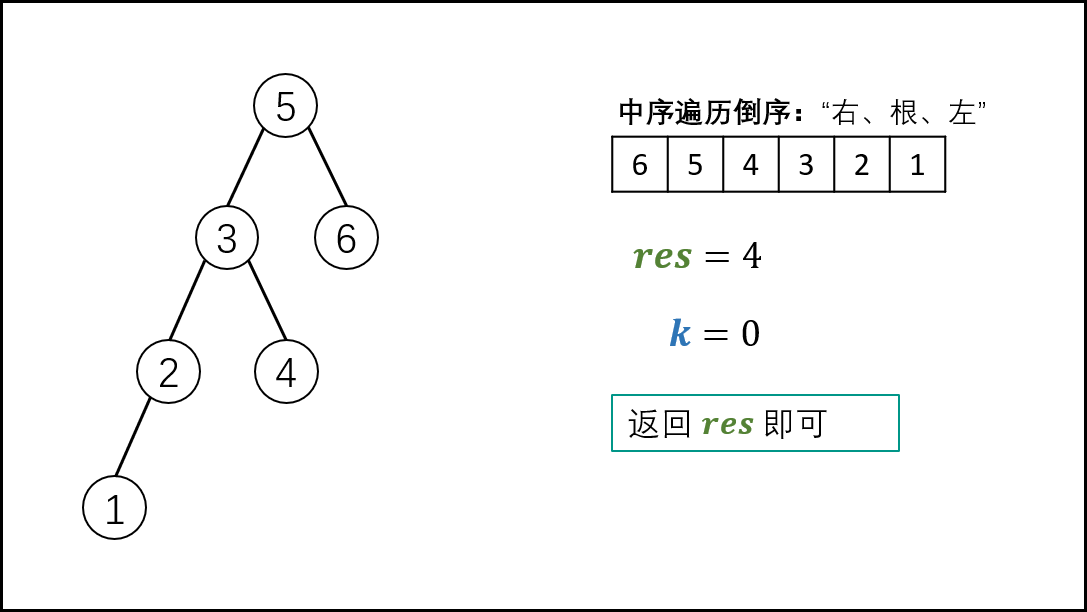
复杂度分析：
时间复杂度 O(N)O(N) ： 当树退化为链表时（全部为右子节点），无论 kk 的值大小，递归深度都为 NN ，占用 O(N)O(N) 时间。
空间复杂度 O(N)O(N) ： 当树退化为链表时（全部为右子节点），系统使用 O(N)O(N) 大小的栈空间。

leetcode 剑指 Offer 26. 树的子结构

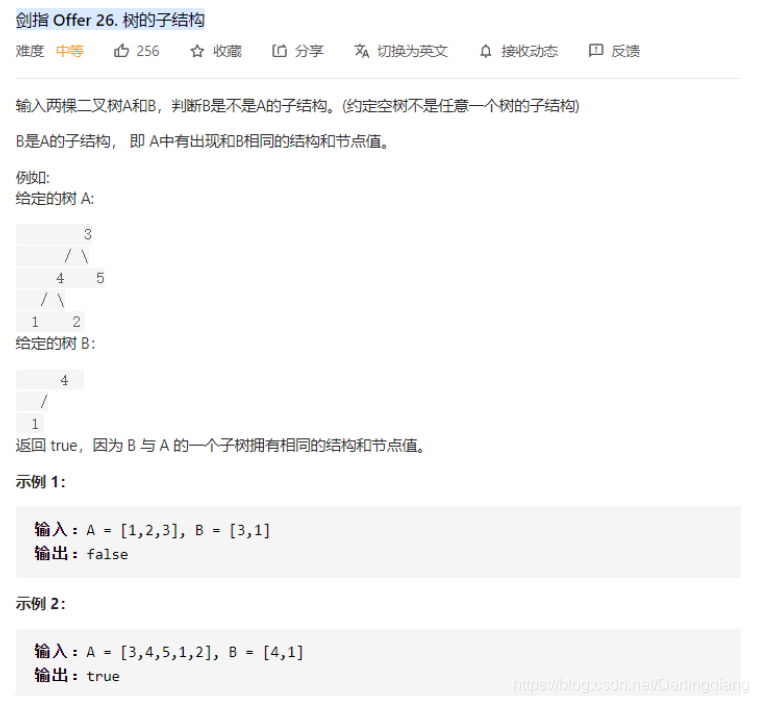
方法1：递归

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool isMatch(TreeNode *A,TreeNode *B){if(B==NULL) return true;if(A==NULL) return false;if(A->val !=B->val) return false;return isMatch(A->left,B->left) && isMatch(A->right,B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {if(B==NULL) return false;if(A==NULL) return false;if(A->val == B->val && isMatch(A,B)) return true;return isSubStructure(A->left,B) || isSubStructure(A->right,B);}
};

 bool isSubStructure(TreeNode* A, TreeNode* B) {if(!A || !B) return false;bool res = false;// 如果在 A 中匹配到了与 B 的根节点的值一样的节点if(A -> val == B -> val) res = doesAHaveB(A, B);// 如果匹配不到，A 往左if(!res) res = isSubStructure(A -> left, B);// 还匹配不到，A 往右if(!res) res = isSubStructure(A -> right, B);return res;}bool doesAHaveB(TreeNode *r1, TreeNode *r2){// 如果 B 已经遍历完了，trueif(!r2) return true;// 如果 B 还有，但 A 遍历完了，那 B 剩下的就没法匹配了，falseif(!r1) return false;// 不相等，falseif(r1 -> val != r2 -> val) return false;return doesAHaveB(r1 -> left, r2 -> left) && doesAHaveB(r1 -> right, r2 -> right);}

leetcode 662. 二叉树最大宽度

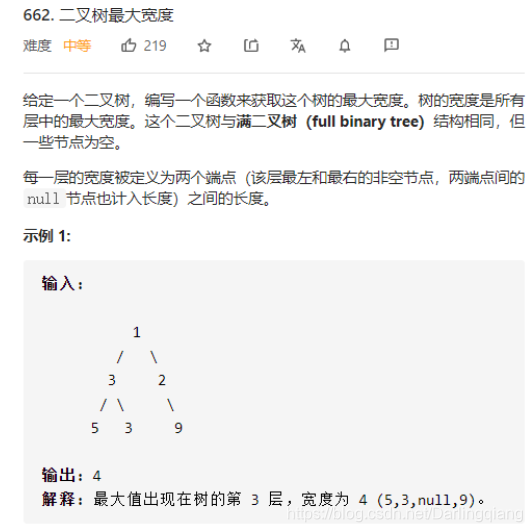
方法 0：宽度优先搜索 [Accepted]

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:typedef pair<TreeNode*,int> PNI;int widthOfBinaryTree(TreeNode* root) {int ans=0;queue<PNI> q;q.push(PNI(root,0));while(!q.empty()){int cnt = q.size();int l=q.front().second,r=q.front().second;for(int i=0;i<cnt;i++){TreeNode *n=q.front().first;int ind=q.front().second;r =ind;if(n->left) q.push(PNI(n->left,(ind-l)*2));if(n->right) q.push(PNI(n->right,(ind-l)*2+1));q.pop();}ans =max(ans,r-l+1);}return ans;}
};

方法框架
解释

由于我们需要将给定树中的每个节点都访问一遍，我们需要遍历树。我们可以用深度优先搜索或者宽度优先搜索将树遍历。

这个问题中的主要想法是给每个节点一个 position 值，如果我们走向左子树，那么 position -> position * 2，如果我们走向右子树，那么 position -> position * 2 + 1。当我们在看同一层深度的位置值 L 和 R 的时候，宽度就是 R - L + 1。

方法 1：宽度优先搜索 [Accepted]

想法和算法

宽度优先搜索顺序遍历每个节点的过程中，我们记录节点的 position 信息，对于每一个深度，第一个遇到的节点是最左边的节点，最后一个到达的节点是最右边的节点。

class Solution {
public:int widthOfBinaryTree(TreeNode* root) {vector<TreeNode*> bfs={root}; //根入队int Depth=0;int max_width=0;while(1){int sum=bfs.size();int start=0,end=0;bool flag=0;int count=0;//遍历当前队列中的元素，即同层的所有节点for(int i=0;i<sum;i++){if(bfs[i]!=NULL){end=i;if(flag==0)  start=i;flag=1;//当前队列的子节点（下一层）入队bfs.push_back(bfs[i]->left);bfs.push_back(bfs[i]->right);}else{count++;//如果为空，那么两个空入队bfs.push_back(NULL);bfs.push_back(NULL);}}if(count==pow(2,Depth))//一层全为空break;if((end-start+1)>max_width)max_width=end-start+1;//当前节点（当前层）出队bfs.erase(bfs.begin(),bfs.begin()+sum);Depth++;}return max_width;}
};

刚开始用BFS做，主要思想就是：把空节点也入队，这样BFS时，就能得到完整的一层节点（空和非空都存在），然后再遍历该层节点，定位宽度即可，但是这样做会因为倒数第二个的变态输入而超时：

复杂度分析

时间复杂度： O(N)O(N)，其中 NN 是输入树的节点数目，我们遍历每个节点一遍。

空间复杂度： O(N)O(N)，这是 queue 的大小。

方法 2：深度优先搜索 [Accepted]

想法和算法

按照深度优先的顺序，我们记录每个节点的 position 。对于每一个深度，第一个到达的位置会被记录在 left[depth] 中。

然后对于每一个节点，它对应这一层的可能宽度是 pos - left[depth] + 1 。我们将每一层这些可能的宽度去一个最大值就是答案。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> left;int max_width=0;void dfs(TreeNode *root, unsigned long long index,int level){if(root ==NULL) return;if(level >left.size())left.push_back(index);if((index-left[level-1]+1)>max_width)max_width=index-left[level-1] +1;dfs(root->left,2*index,level+1);dfs(root->right,2*index+1,level+1);}int widthOfBinaryTree(TreeNode* root) {if(root ==NULL) return 0;dfs(root,1,1);return max_width;}
};

只需要利用树和数组转换关系：若假设当前节点在数组中的下标为i，那么左节点为下标为：2i，右节点为：2i+1
此外，还需要用一个容器保存每层最左节点的下标，容器的大小就是遍历的深度，这样遍历每个节点时，比较当前下标-最左节点下标+1和最大宽度，取较大者，就可以得到树的最大宽度。
那么怎么判断当前节点是该层最左节点？根据前序遍历的特点，最左节点一定是同层中第一个出现的节点，也就是level大于容器大小时，left容器push一个当前下标，这样再遍历同层其他节点时，由于left已经push了一个，该判断也就不会为真了。

leetcode 968. 监控二叉树

第一种解法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Zs0HVPbY-1619446816633)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\1619222543902.png)]

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:void getDP(TreeNode* root,int dp[2][2]){//dp[0][0] //父节点不放摄像头，本节点也不放摄像头，像覆盖掉所有子树，最少放置的摄像头数量//dp数组中存放的摄像头数量 为当前节点的数量，只能为0或者1，10000表示当前这种状态不存在if(root ==NULL){dp[0][0] =0;dp[0][1] =10000;dp[1][0] =0;dp[1][1] =10000;return;}if(root->left ==NULL && root->right ==NULL){dp[0][0] =10000;dp[0][1] =1;dp[1][0] =0;dp[1][1] =1;}int l[2][2],r[2][2];getDP(root->left,l);getDP(root->right,r);dp[0][0] =min(min(l[0][1]+r[0][0],l[0][0]+r[0][1]),l[0][1]+r[0][1]);//表示三种状态取最小，l[0][1]表示父节点不放，当前左节点放；r[0][1]表示父节点不放，当		  //前右节点放dp[1][0] =min(dp[0][0],l[0][0]+r[0][0]);//dp[1][0]4种情况，表示当前节点的子节点放不放均可dp[0][1] =min(min(l[1][0]+r[1][0],l[1][1]+r[1][1]),min(l[1][0]+r[1][1],l[1][1]+r[1][0]))+1;//求4种情况下和的最小值，前面2种情况，要么多放，要么都不放；后面2种情况一个放，一个不放；dp[1][1] =dp[0][1];//当前节点放一个摄像头，可以覆盖周围return;}int minCameraCover(TreeNode* root) {int dp[2][2];getDP(root,dp);return min(dp[0][1],dp[0][0]);}
};

解题思路
这道题目其实不是那么好理解的，题目举的示例不是很典型，会误以为摄像头必须要放在中间，其实放哪里都可以只要覆盖了就行。

这道题目难在两点：

需要确定遍历方式
需要状态转移的方程
我们之前做动态规划的时候，只要最难的地方在于确定状态转移方程，至于遍历方式无非就是在数组或者二维数组上。

本题并不是动态规划，其本质是贪心，但我们要确定状态转移方式，而且要在树上进行推导，所以难度就上来了，一些同学知道这道题目难，但其实说不上难点究竟在哪。

需要确定遍历方式
首先先确定遍历方式，才能确定转移方程，那么该如何遍历呢？

在安排选择摄像头的位置的时候，我们要从底向上进行推导，因为尽量让叶子节点的父节点安装摄像头，这样摄像头的数量才是最少的 ，这也是本道贪心的原理所在！

如何从低向上推导呢？

就是后序遍历也就是左右中的顺序，这样就可以从下到上进行推导了。

后序遍历代码如下：

    int traversal(TreeNode* cur) {// 空节点，该节点有覆盖if (终止条件) return ;int left = traversal(cur->left);    // 左int right = traversal(cur->right);  // 右逻辑处理                            // 中return ;}

注意在以上代码中我们取了左孩子的返回值，右孩子的返回值，即 left 和 right， 以后推导中间节点的状态

需要状态转移的方程
确定了遍历顺序，再看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

可以说有如下三种：

该节点无覆盖
本节点有摄像头
本节点有覆盖
我们分别有三个数字来表示：

0：该节点无覆盖
1：本节点有摄像头
2：本节点有覆盖
大家应该找不出第四个节点的状态了。

一些同学可能会想有没有第四种状态：本节点无摄像头，其实无摄像头就是 无覆盖 或者 有覆盖的状态，所以一共还是三个状态。

那么问题来了，空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

回归本质，为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

那么空节点不能是无覆盖的状态，这样叶子节点就可以放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。

所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了

接下来就是递推关系。

那么递归的终止条件应该是遇到了空节点，此时应该返回 2（有覆盖），原因上面已经解释过了。

代码如下：

        // 空节点，该节点有覆盖if (cur == NULL) return 2;

递归的函数，以及终止条件已经确定了，再来看单层逻辑处理。

主要有如下四类情况：

情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

代码如下：

        // 左右节点都有覆盖if (left == 2 && right == 2) return 0;

情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

left == 0 && right == 0 左右节点无覆盖
left == 1 && right == 0 左节点有摄像头，右节点无覆盖
left == 0 && right == 1 左节点有无覆盖，右节点摄像头
left == 0 && right == 2 左节点无覆盖，右节点覆盖
left == 2 && right == 0 左节点覆盖，右节点无覆盖

这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。

此时摄像头的数量要加一，并且 return 1，代表中间节点放摄像头。

代码如下：

    if (left == 0 || right == 0) {result++;return 1;}

情况3：左右节点至少有一个有摄像头

如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

left == 1 && right == 2 左节点有摄像头，右节点有覆盖
left == 2 && right == 1 左节点有覆盖，右节点有摄像头
left == 1 && right == 1 左右节点都有摄像头

代码如下：

    if (left == 1 || right == 1) return 2;

从这个代码中，可以看出，如果 left == 1, right == 0 怎么办？其实这种条件在情况 2 中已经判断过了，如图：

这种情况也是大多数同学容易迷惑的情况。

情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

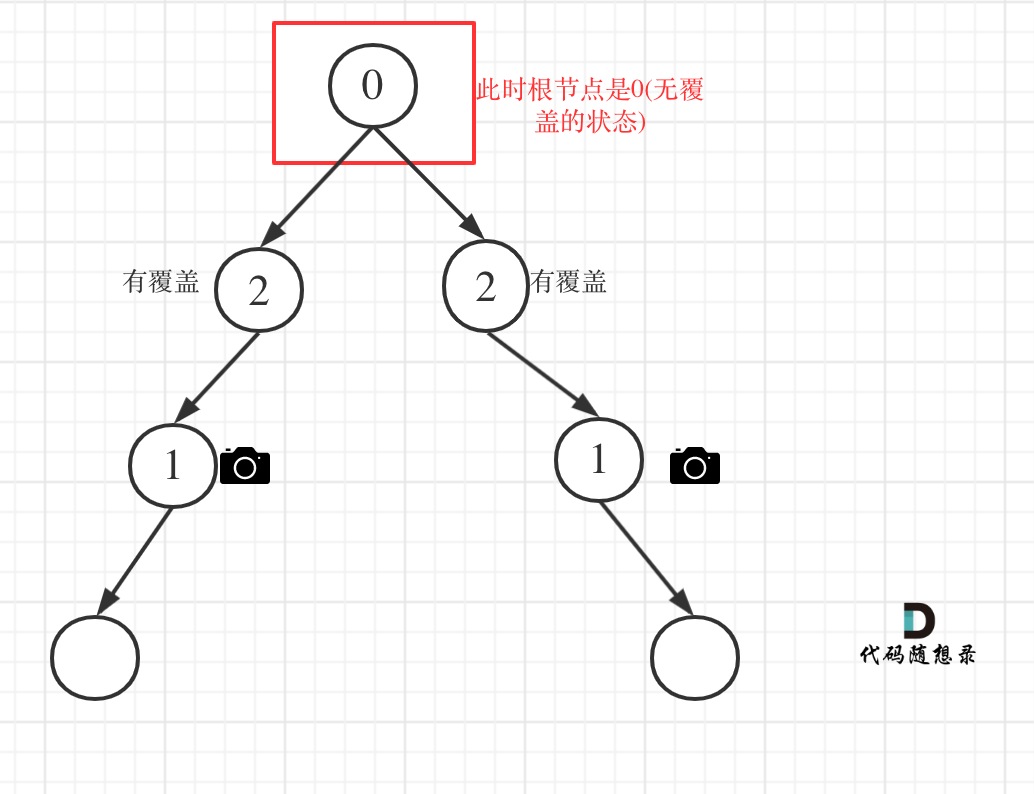
所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;
}

以上四种情况我们分析完了，代码也差不多了，整体代码如下：

（以下我的代码是可以精简的，但是我是为了把情况说清楚，特别把每种情况列出来，因为精简之后的代码读者不好理解。）

C++

class Solution {
private:
int result;
int traversal(TreeNode* cur) {

    // 空节点，该节点有覆盖if (cur == NULL) return 2;int left = traversal(cur->left);    // 左int right = traversal(cur->right);  // 右// 情况1// 左右节点都有覆盖if (left == 2 && right == 2) return 0;// 情况2// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头，右节点无覆盖// left == 0 && right == 1 左节点有无覆盖，右节点摄像头// left == 0 && right == 2 左节点无覆盖，右节点覆盖// left == 2 && right == 0 左节点覆盖，右节点无覆盖if (left == 0 || right == 0) {result++;return 1;}// 情况3// left == 1 && right == 2 左节点有摄像头，右节点有覆盖// left == 2 && right == 1 左节点有覆盖，右节点有摄像头// left == 1 && right == 1 左右节点都有摄像头// 其他情况前段代码均已覆盖if (left == 1 || right == 1) return 2;// 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解// 这个 return -1 逻辑不会走到这里。return -1;
}
public:int minCameraCover(TreeNode* root) {result = 0;// 情况4if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};

t == 0 || right == 0) {
result++;
return 1;
}

情况3：左右节点至少有一个有摄像头

如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

left == 1 && right == 2 左节点有摄像头，右节点有覆盖
left == 2 && right == 1 左节点有覆盖，右节点有摄像头
left == 1 && right == 1 左右节点都有摄像头

代码如下：

    if (left == 1 || right == 1) return 2;

从这个代码中，可以看出，如果 left == 1, right == 0 怎么办？其实这种条件在情况 2 中已经判断过了，如图：

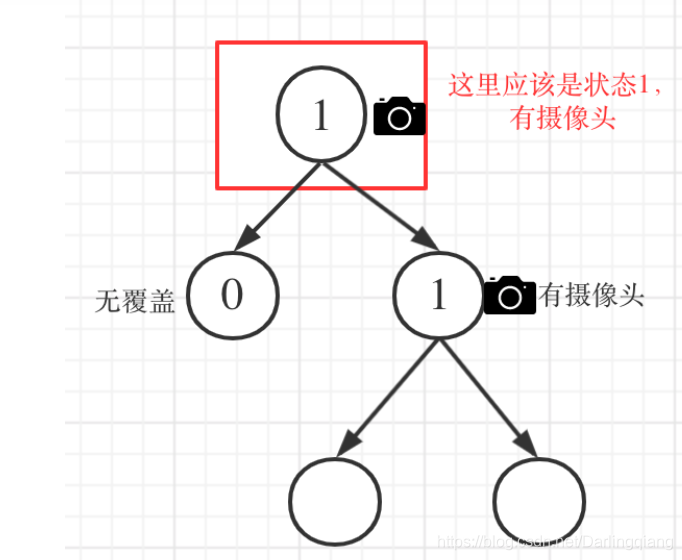
这种情况也是大多数同学容易迷惑的情况。

情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

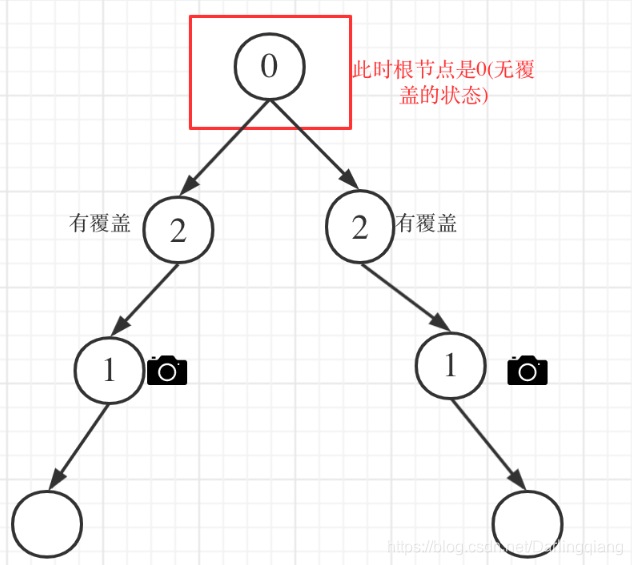
所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;
}

以上四种情况我们分析完了，代码也差不多了，整体代码如下：

（以下我的代码是可以精简的，但是我是为了把情况说清楚，特别把每种情况列出来，因为精简之后的代码读者不好理解。）

C++

class Solution {
private:
int result;
int traversal(TreeNode* cur) {

    // 空节点，该节点有覆盖if (cur == NULL) return 2;int left = traversal(cur->left);    // 左int right = traversal(cur->right);  // 右// 情况1// 左右节点都有覆盖if (left == 2 && right == 2) return 0;// 情况2// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头，右节点无覆盖// left == 0 && right == 1 左节点有无覆盖，右节点摄像头// left == 0 && right == 2 左节点无覆盖，右节点覆盖// left == 2 && right == 0 左节点覆盖，右节点无覆盖if (left == 0 || right == 0) {result++;return 1;}// 情况3// left == 1 && right == 2 左节点有摄像头，右节点有覆盖// left == 2 && right == 1 左节点有覆盖，右节点有摄像头// left == 1 && right == 1 左右节点都有摄像头// 其他情况前段代码均已覆盖if (left == 1 || right == 1) return 2;// 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解// 这个 return -1 逻辑不会走到这里。return -1;
}
public:int minCameraCover(TreeNode* root) {result = 0;// 情况4if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};