贝叶斯定理——数学之美
1.贝叶斯定理
1.1 定义:描述在已知一些条件下,某事件的发生概率
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
1.2 公式理解
P(x∣y)=P(x)P(y∣x)P(y)P(x|y) =\frac{ P(x)P(y|x)}{P(y)}P(x∣y)=P(y)P(x)P(y∣x)
其中x以及y为随机事件,且P(y)P(y)P(y)不为零。P(x∣y)P(x|y)P(x∣y)是指在y事件发生的情况下,x事件发生的概率。
其中:
P(x∣y)P(x|y)P(x∣y)是已知y发生后,x的条件概率。也称作x的后验概率。
P(x)P(x)P(x)是x的先验概率(或边缘概率)。其不考虑任何y方面的因素。即x与y相互独立
P(y∣x)P(y|x)P(y∣x)是已知x发生后,y的条件概率。也可称为y的后验概率。
P(y)P(y)P(y)是y的先验概率。
贝叶斯定理可表述为:
后验概率 = (似然性*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
2.贝叶斯理论推导(从条件概率)
2.1 推到
根据条件概率的定义。在事件y发生的条件下事件x发生的概率是:
P(x∣y)=P(x∩y)P(y)P(x|y)=\frac{P(x \cap y)}{P(y)}P(x∣y)=P(y)P(x∩y)
其中 A与B的联合概率表示为P(x∩y)P(x \cap y)P(x∩y)或者p(x,y)p(x,y)p(x,y)或者p(xy)p(xy)p(xy)。
同样地,在事件x发生的条件下事件y发生的概率
P(y∣x)=P(y∩x)P(x)P(y|x)=\frac{P(y \cap x)}{P(x)}P(y∣x)=P(x)P(y∩x)
联立可得
P(x∣y)P(y)=P(x∩y)=P(y∣x)P(x)P(x|y){P(y)}={P(x \cap y)} = P(y|x){P(x)}P(x∣y)P(y)=P(x∩y)=P(y∣x)P(x) 若P(y)≠0P(y) \neq 0P(y)=0则
P(x∣y)=P(x)P(y∣x)P(y)P(x|y) =\frac{ P(x)P(y|x)}{P(y)}P(x∣y)=P(y)P(x)P(y∣x)得证
2.2 贝叶斯理论的推广
P(x∣y,z)=P(x,y,z)P(y,z)P(x| y, z) = \frac{P(x, y, z)}{P(y, z)}P(x∣y,z)=P(y,z)P(x,y,z)
=P(x,y,z)P(y)P(z∣y)= \frac{P(x, y, z)}{{P(y)} P(z| y)}=P(y)P(z∣y)P(x,y,z)
=P(z∣x,y)P(x,y)P(y)P(z∣y)= \frac{P(z| x, y) P(x,y)}{{P(y)} P(z| y)}=P(y)P(z∣y)P(z∣x,y)P(x,y)
=P(x)P(y∣x)P(z∣x,y)P(y)P(z∣y)= \frac{{P(x) P(y| x) P(z|x,y)}}{{P(y)} P(z| y)}=P(y)P(z∣y)P(x)P(y∣x)P(z∣x,y)
一般化的方法则是利用联合概率去分解待求的条件概率,并对不加以探讨的变量积分(意即对欲探讨的变量计算边缘概率)。取决于不同的分解形式,可以证明某些积分必为1,因此分解形式可被简化。利用这个性质,贝叶斯理论的计算量可能可以大幅下降。贝叶斯网络为此方法的一个例子,贝叶斯网络指定数个变量的联合概率分布的分解型式,该概率分布满足下述条件:当其他变量的条件概率给定时,该变量的条件概率为一简单型式。
3 贝叶斯公式理解实例
3.1 通过开车过程中对十字路口来理解贝叶斯公式

P(A∣B)=P(A)P(B∣A)P(B)P(A|B) =\frac{ P(A)P(B|A)}{P(B)}P(A∣B)=P(B)P(A)P(B∣A)
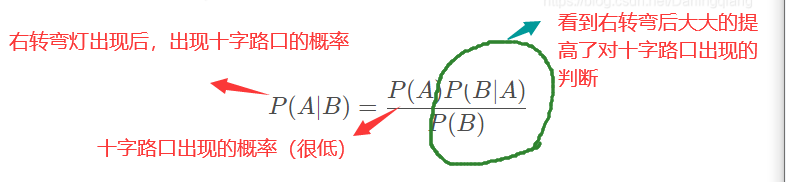
因此贝叶斯公式实际上阐述了这么一个事情:
新信息出现后对A事件的概率预测 = A事件的鲜艳概率 * 新信息带来的调整
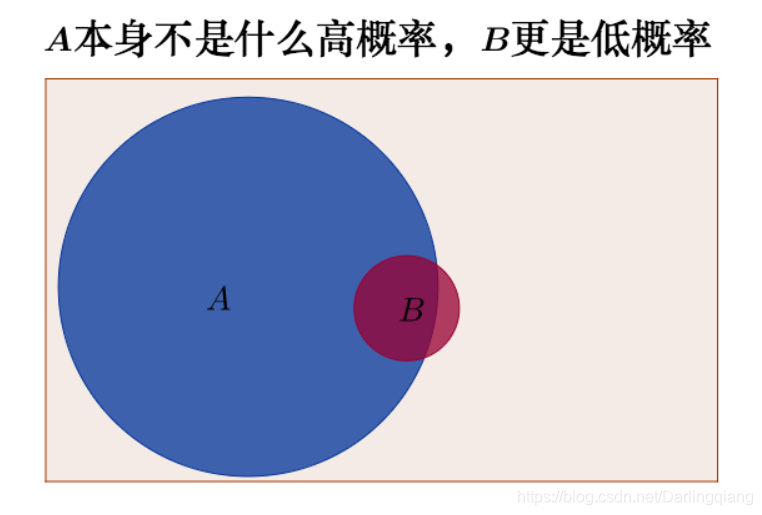
我们再通过韦恩图来理解一下这个事情(为了观看方便,下面的A,B的圆形面积是示意):
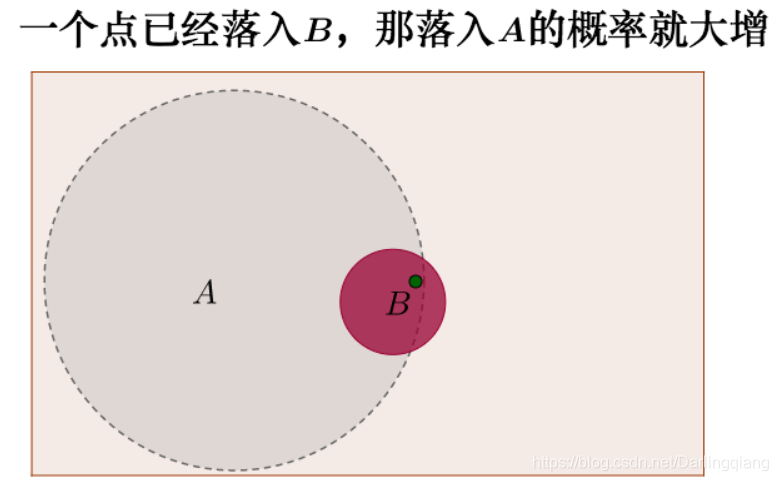
新的信息的出现,比如之前看到了亮着右转弯灯的车,就好比知道点已经落入了B。
3.2 实例理解贝叶斯公式小结
可以看到,有形的十字路口,却看不到明天是否下雨,我们可以看到前方是否有路障,却不清楚下一次飞机是否会出事。甚至有时候,眼睛还会欺骗我们。
很多时候,我们不得不看着后视镜开车,这个时候概率论、贝叶斯定理就是我们的指路明灯。
看着后视镜开车,肯定常常会撞车,没关系,我们可以不断的去修正我们的假设。
比如,撞了几次车之后,就发现可能之前估计的在十字路口打右转弯灯的数据明显偏大了,我们修正之后再继续开车。我们人类的学习,本身也是一个试错的过程。
参考资料
数学之美番外篇:平凡而又神奇的贝叶斯方法
概率机器人
如何理解贝叶斯定理?
数学之美番外篇:平凡而又神奇的贝叶斯方法
相关文章:

HUST 1586 数字排列
1586 - 数字排列 时间限制:1秒 内存限制:128兆 91 次提交 36 次通过 题目描述现有n个k位的数字,你的任务是重新安排数字每一位的位置,使得重新安排后这n个数字中最大的数字和最小的数字之差的绝对值最小,对于每一位的调…

最小矩形与圆生成1
#include <opencv2/imgproc/imgproc.hpp> #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <iostream> #include <stdio.h> using namespace cv; using namespace std; // 计算外接矩形与圆轮廓…

kettle-核心概念
转载于:https://www.cnblogs.com/LXL616/p/10836183.html

adb调试命令小结
adb调试命令 adb 连接android设备 adb connect 192.168.103.246 connected to 192.168.103.246:5555 sunsun:~/workspace/deptrum$ adb connect 192.168.103.246:5555 already connected to 192.168.103.246:5555 sunsun:~/workspace/deptrum$ adb shell tb8788p1_64_bsp_wxp…

github创建本地库后关联远程库
在进行新项目开发时,有时候并不一定先创建远程库,而是先在本地将项目创建,到一定阶段后再与远程库关联。下面步骤解决本地库与远程库在这种情形。 1. 初始化本地库,既然项目已经创建了,相信这个也已经知道了。 git ini…

mysql以及mysql bench安装教程
首先,我们需要去官网下载mysql(这里以下载) 1 2 3 4 5 下载好了自己好了之后,点击安装好的东西出现如下界面: 1、接受使用条款并点击next 2、点击custom,可以根据个人习惯进行安装 3、这里来是需要安装的一…
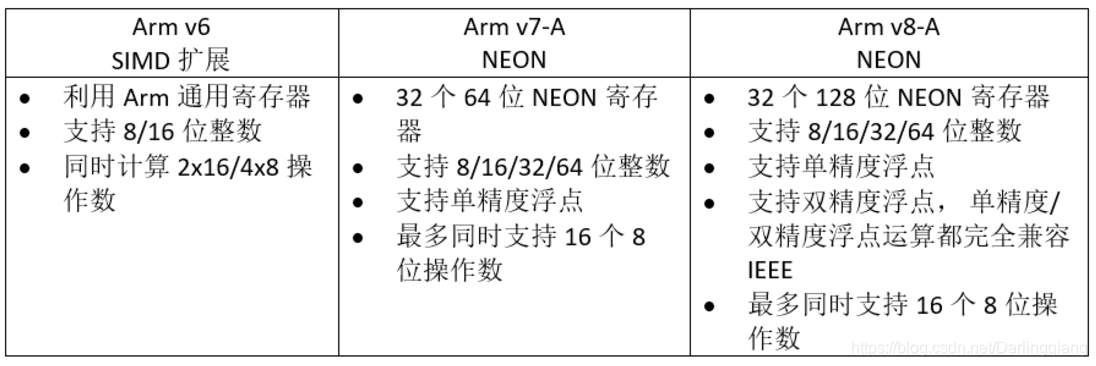
【NEON 】初探
NEON 文章目录NEON1 neon窥探1.1 neon用途1.2 neon处理机制1.3 neon发展历程中的优缺点对比1.4 为什么使用neon1.5 Armv7/v8详细差异1.6 Register寄存器1.7 指令系统间的关系与1.3相似2 neon 使用2.1 neon 指令格式2.2 AArch64 NEON 指令语法2.3 NEON 指令3.1 RK3399资料1 neon…

sql 常用 语法
2019独角兽企业重金招聘Python工程师标准>>> 1. 字段 不重复 ALTER TABLE sys_workday ADD UNIQUE (ymd) ; 转载于:https://my.oschina.net/u/1760858/blog/838385

moravec 角点检测
#include <opencv2/opencv.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/imgproc/imgproc.hpp> using namespace std; using namespace cv; // MoravecCorners角点检测 cv::Mat MoravecCorners(cv::Mat srcImage, int kSize, int thresho…

js控制视频播放
2019独角兽企业重金招聘Python工程师标准>>> 1、js控制视频播放 1、页面html <div id"slide" class"videoWrap"></div><canvas v-show"!isShowVideoCover" id"canvas" class"videoCanvas"><…
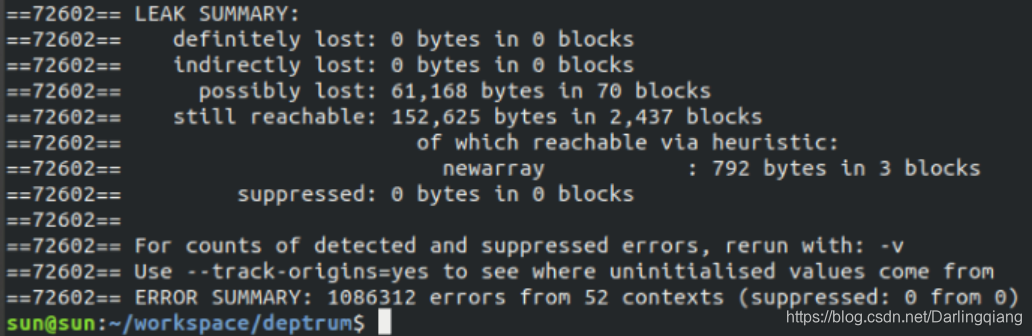
valgrind-yyds——memcheck检查程序中的内存问题,如泄漏、越界、非法指针等。
Valgrind 用户手册 文章目录1. valgrind概述2. Valgrind 原理及安装2.1 [Valgrind 做了什么](https://www.valgrind.org/docs/manual/manual-core.html)2.2 安装3 内存检测3.1 memcheck 常用检测指令3 .2 内存检测结果3 .3 内存检测含义3 .4 内存检测更多例子1. valgrind概述 …
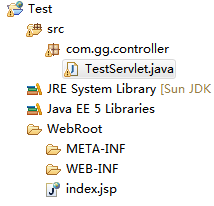
数据传送到后端(二)
先在myeclipse里建立上图文件,然后在TestServlet.java里面的doGet{}括号里面填入以下内容: public void doGet(HttpServletRequest request, HttpServletResponse response) throws ServletException, IOException { //解决中文乱码 request.setCharacte…

HSV 通道分离
// 转换成hsv cv::Mat img_h, img_s, img_v, imghsv;std::vector<cv::Mat> hsv_vec;cv::cvtColor(srcImage, imghsv, CV_BGR2HSV);cv::imshow("hsv", imghsv);cv::waitKey(0);// 分割hsv通道cv::split(imghsv, hsv_vec);img_h hsv_vec[0];img_s hsv_vec[1];i…

阿里云安全肖力:安全基础建设是企业数字化转型的基石
2019独角兽企业重金招聘Python工程师标准>>> 企业在享受数字化转型带来利好的同时,其面临的安全问题也愈发复杂。一方面,外部威胁不断升级,近期利用海量移动设备发起DDoS攻击的案例表明,黑灰产作案手法也在随着时代的发…
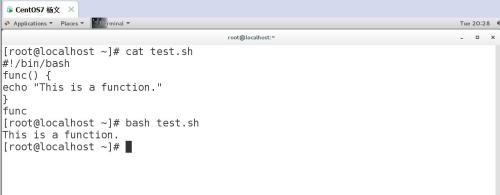
Shell 函数、数组与正则表达式
防伪码:白日依山尽,黄河入海流。5.1 函数格式:func() {command}示例 1:#!/bin/bashfunc() {echo "This is a function."}func# bash test.shThis is a function.Shell 函数很简单,函数名后跟双括号…
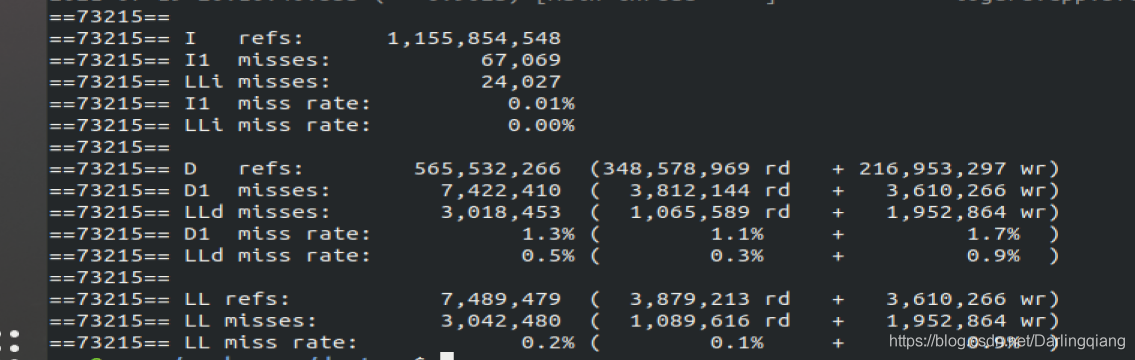
valgrind——Cachegrind分析CPU的cache命中率、丢失率,用于进行代码优化。
功能扩展1 Cachegrind 1.1 指令范式 单行最重要指令: valgrind --tool [default: memcheck] sunsun:~/workspace/deptrum$ valgrind --tool //table 查看工具 cachegrind callgrind drd exp-bbv exp-dhat exp-sgcheck getoff he…

细化 Sobel 边缘提取
bool SobelVerEdge(cv::Mat srcImage, cv::Mat& resultImage) {CV_Assert(srcImage.channels() 1);srcImage.convertTo(srcImage, CV_32FC1);// 水平方向的 Sobel 算子cv::Mat sobelx (cv::Mat_<float>(3, 3) << -0.125, 0, 0.125,-0.25, 0, 0.25,-0.125, 0,…

PRD 的编写和修改注意事项
2019独角兽企业重金招聘Python工程师标准>>> 每个操作的发生时机(状态)要搞清楚,表达逻辑时一定要用准确的词语,避免对自己和别人造成误会。状态图,标识状态的流转和事件发生点评审PRD时最好记录下修改的内…
valgrind——Callgrind检测程序代码的运行时间和调用过程,程序分析性能。
功能扩展1 callgrind 1.1 指令范式 valgrind --toolcallgrind --separate-threadsyes ./run1.2 install sudo apt-get update -y sudo apt-get install -y kcachegrind ref: 1.3 分析工具Kcachegrind Callgrind通过Valgrind框架使用运行时检测来进行缓存模拟和调用图生成…

车牌疑似区域点提取
// hsv 限定范围元素提取cv::Mat bw_blue ((img_h>0.45) &(img_h<0.75) &(img_s>0.15) &(img_v>0.25));int height bw_blue.rows;int width bw_blue.cols;cv::Mat bw_blue_edge cv::Mat::zeros(bw_blue.size(), bw_blue.type());cv::imshow("…

MySQL编码引发的两个问题
2019独角兽企业重金招聘Python工程师标准>>> 概述 先讲一下写该文章的原因,首先,工作中又遇到一条很熟悉的MySQL报错信息 Cause: java.sql.SQLException: Incorrect string value:Cause: java.sql.SQLException: Incorrect string value… &a…

valgrind——hisi平台valgrind
valgrind——hisi平台valgrind https://blog.csdn.net/lizhangping/article/details/51833997

Java23种设计模式学习笔记【目录总贴】
创建型模式:关注对象的创建过程 1、单例模式:保证一个类只有一个实例,并且提供一个访问该实例的全局访问点 主要: 饿汉式(线程安全,调用效率高,但是不能延时加载) 懒汉式ÿ…

Hystrix 超时配置重写
2019独角兽企业重金招聘Python工程师标准>>> Configuration ConditionalOnProperty(value "spring.sleuth.feign.enabled", havingValue "false") Slf4j public class CommonHystrixConfiguration {/*** hystrix 超时时间*/static int hystri…
Linux系统/boot目录破损无法启动怎么办
豌豆贴心提醒,本文阅读时间5分钟,文末有秘密!linux系统中的/boot目录存放着系统开机所需要的各种文件,其中包含内核、开机菜单及所需配置文件等等。但是当不小心删除了/boot目录里的某些文件或者干脆整个/boot目录都不见了的情况下…

分水岭图像分割
Mat watershedSegment(Mat & srcImage, int & noOfSegments) {Mat grayMat;Mat otsuMat;cvtColor(srcImage, grayMat, CV_BGR2GRAY);imshow("grayMat", grayMat);// 阈值操作threshold(grayMat, otsuMat, 0, 255, CV_THRESH_BINARY_INV CV_THRESH_OTSU);ims…

linux(armv7/8)下gdb的安装及查看方法
1. gdb安装 1.1 将gdb-10.1.tar.gz拷贝的/usr/local/目录下 (可以拷贝到任何你愿意的Linux目录下)或者进入 /usr/local中下载地址:http://ftp.gnu.org/gnu/gdb/ sudo wget http://ftp.gnu.org/gnu/gdb/gdb-10.1.tar.gz1.2 解压 gdb-10.1.t…

【数据排序】车厢重组
车厢重组 【题目描述】 在一个旧式的火车站旁边有一座桥,其桥面可以绕河中心的桥墩水平旋转。一个车站的职工发现桥的长度最多能容纳两节车厢,如果将桥旋转180度,则可以把相邻两节车厢的位置交换,用这种方法可以重新排列车厢的顺序…

adb部署记录
文章目录[1 \[NDK部署\]](https://dl.google.com/android/repository/android-ndk-r10e-linux-x86_64.zip?hlzh_cn)1.1 首先在本地部署adb(NDK,已经完成编译,可以直接运行)1.2 其次在远端部署 gdbserver2 系统依赖配置2.1 拉去远…

“”开天眼“”,天地分割效果
每日一句:Node.js uses an event-driven, non-blocking I/O model that makes it lightweight and efficient. (源于:nodejs的官网) 翻译:nodejs使用了事件驱动,非阻塞I/o的模型,这些模型是的它运行起来轻便而且有效率…
