Numpy入门教程:10. 统计相关
背景
什么是 NumPy 呢?
NumPy 这个词来源于两个单词 – Numerical和Python。其是一个功能强大的 Python 库,可以帮助程序员轻松地进行数值计算,通常应用于以下场景:
- 执行各种数学任务,如:数值积分、微分、内插、外推等。因此,当涉及到数学任务时,它形成了一种基于 Python 的 MATLAB 的快速替代。
- 计算机中的图像表示为多维数字数组。NumPy 提供了一些优秀的库函数来快速处理图像。例如,镜像图像、按特定角度旋转图像等。
- 在编写机器学习算法时,需要对矩阵进行各种数值计算。如:矩阵乘法、求逆、换位、加法等。NumPy 数组用于存储训练数据和机器学习模型的参数。
统计相关
次序统计
numpy.amin(a[, axis=None, out=None, keepdims=np._NoValue, initial=np._NoValue, where=np._NoValue])Return the minimum of an array or minimum along an axis.
【例】计算最小值
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.amin(x)
print(y) # 11y = np.amin(x, axis=0)
print(y) # [11 12 13 14 15]y = np.amin(x, axis=1)
print(y) # [11 16 21 26 31]
numpy.amax(a[, axis=None, out=None, keepdims=np._NoValue, initial=np._NoValue, where=np._NoValue])Return the maximum of an array or maximum along an axis.
【例】计算最大值
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.amax(x)
print(y) # 35y = np.amax(x, axis=0)
print(y) # [31 32 33 34 35]y = np.amax(x, axis=1)
print(y) # [15 20 25 30 35]
numpy.ptp(a, axis=None, out=None, keepdims=np._NoValue)Range of values (maximum - minimum) along an axis. The name of the function comes from the acronym for ‘peak to peak’.
【例】计算极差
import numpy as npnp.random.seed(20200623)
x = np.random.randint(0, 20, size=[4, 5])
print(x)
# [[10 2 1 1 16]
# [18 11 10 14 10]
# [11 1 9 18 8]
# [16 2 0 15 16]]print(np.ptp(x)) # 18
print(np.ptp(x, axis=0)) # [ 8 10 10 17 8]
print(np.ptp(x, axis=1)) # [15 8 17 16]
numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)Compute the q-th percentile of the data along the specified axis. Returns the q-th percentile(s) of the array elements.- a:array,用来算分位数的对象,可以是多维的数组。
- q:介于0-100的float,用来计算是几分位的参数,如四分之一位就是25,如要算两个位置的数就[25,75]。
- axis:坐标轴的方向,一维的就不用考虑了,多维的就用这个调整计算的维度方向,取值范围0/1。
【例】计算分位数
import numpy as npnp.random.seed(20200623)
x = np.random.randint(0, 20, size=[4, 5])
print(x)
# [[10 2 1 1 16]
# [18 11 10 14 10]
# [11 1 9 18 8]
# [16 2 0 15 16]]print(np.percentile(x, [25, 50]))
# [ 2. 10.]print(np.percentile(x, [25, 50], axis=0))
# [[10.75 1.75 0.75 10.75 9.5 ]
# [13.5 2. 5. 14.5 13. ]]print(np.percentile(x, [25, 50], axis=1))
# [[ 1. 10. 8. 2.]
# [ 2. 11. 9. 15.]]
均值与方差
numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)Compute the median along the specified axis. Returns the median of the array elements.
【例】计算中位数
import numpy as npnp.random.seed(20200623)
x = np.random.randint(0, 20, size=[4, 5])
print(x)
# [[10 2 1 1 16]
# [18 11 10 14 10]
# [11 1 9 18 8]
# [16 2 0 15 16]]
print(np.percentile(x, 50))
print(np.median(x))
# 10.0print(np.percentile(x, 50, axis=0))
print(np.median(x, axis=0))
# [13.5 2. 5. 14.5 13. ]print(np.percentile(x, 50, axis=1))
print(np.median(x, axis=1))
# [ 2. 11. 9. 15.]
numpy.mean(a[, axis=None, dtype=None, out=None, keepdims=np._NoValue)])Compute the arithmetic mean along the specified axis.
【例】计算平均值(沿轴的元素的总和除以元素的数量)。
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.mean(x)
print(y) # 23.0y = np.mean(x, axis=0)
print(y) # [21. 22. 23. 24. 25.]y = np.mean(x, axis=1)
print(y) # [13. 18. 23. 28. 33.]
numpy.average(a[, axis=None, weights=None, returned=False])Compute the weighted average along the specified axis.
mean和average都是计算均值的函数,在不指定权重的时候average和mean是一样的。指定权重后,average可以计算加权平均值。
【例】计算加权平均值(将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。)
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.average(x)
print(y) # 23.0y = np.average(x, axis=0)
print(y) # [21. 22. 23. 24. 25.]y = np.average(x, axis=1)
print(y) # [13. 18. 23. 28. 33.]y = np.arange(1, 26).reshape([5, 5])
print(y)
# [[ 1 2 3 4 5]
# [ 6 7 8 9 10]
# [11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]]z = np.average(x, weights=y)
print(z) # 27.0z = np.average(x, axis=0, weights=y)
print(z)
# [25.54545455 26.16666667 26.84615385 27.57142857 28.33333333]z = np.average(x, axis=1, weights=y)
print(z)
# [13.66666667 18.25 23.15384615 28.11111111 33.08695652]
numpy.var(a[, axis=None, dtype=None, out=None, ddof=0, keepdims=np._NoValue])Compute the variance along the specified axis.- ddof=0:是“Delta Degrees of Freedom”,表示自由度的个数。
要注意方差和样本方差的无偏估计,方差公式中分母上是n;样本方差无偏估计公式中分母上是n-1(n为样本个数)。
【例】计算方差
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.var(x)
print(y) # 52.0
y = np.mean((x - np.mean(x)) ** 2)
print(y) # 52.0y = np.var(x, ddof=1)
print(y) # 54.166666666666664
y = np.sum((x - np.mean(x)) ** 2) / (x.size - 1)
print(y) # 54.166666666666664y = np.var(x, axis=0)
print(y) # [50. 50. 50. 50. 50.]y = np.var(x, axis=1)
print(y) # [2. 2. 2. 2. 2.]
numpy.std(a[, axis=None, dtype=None, out=None, ddof=0, keepdims=np._NoValue])Compute the standard deviation along the specified axis.
标准差是一组数据平均值分散程度的一种度量,是方差的算术平方根。
【例】计算标准差
import numpy as npx = np.array([[11, 12, 13, 14, 15],[16, 17, 18, 19, 20],[21, 22, 23, 24, 25],[26, 27, 28, 29, 30],[31, 32, 33, 34, 35]])
y = np.std(x)
print(y) # 7.211102550927978
y = np.sqrt(np.var(x))
print(y) # 7.211102550927978y = np.std(x, axis=0)
print(y)
# [7.07106781 7.07106781 7.07106781 7.07106781 7.07106781]y = np.std(x, axis=1)
print(y)
# [1.41421356 1.41421356 1.41421356 1.41421356 1.41421356]
相关
numpy.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None,aweights=None)Estimate a covariance matrix, given data and weights.
【例】计算协方差矩阵
import numpy as npx = [1, 2, 3, 4, 6]
y = [0, 2, 5, 6, 7]
print(np.cov(x)) # 3.7
print(np.cov(y)) # 8.5
print(np.cov(x, y))
# [[3.7 5.25]
# [5.25 8.5 ]]print(np.var(x)) # 2.96
print(np.var(x, ddof=1)) # 3.7
print(np.var(y)) # 6.8
print(np.var(y, ddof=1)) # 8.5z = np.mean((x - np.mean(x)) * (y - np.mean(y)))
print(z) # 4.2z = np.sum((x - np.mean(x)) * (y - np.mean(y))) / (len(x) - 1)
print(z) # 5.25z = np.dot(x - np.mean(x), y - np.mean(y)) / (len(x) - 1)
print(z) # 5.25
numpy.corrcoef(x, y=None, rowvar=True, bias=np._NoValue, ddof=np._NoValue)Return Pearson product-moment correlation coefficients.
理解了np.cov()函数之后,很容易理解np.correlate(),二者参数几乎一模一样。
np.cov()描述的是两个向量协同变化的程度,它的取值可能非常大,也可能非常小,这就导致没法直观地衡量二者协同变化的程度。相关系数实际上是正则化的协方差,n个变量的相关系数形成一个n维方阵。
【例】计算相关系数
import numpy as npnp.random.seed(20200623)
x, y = np.random.randint(0, 20, size=(2, 4))print(x) # [10 2 1 1]
print(y) # [16 18 11 10]z = np.corrcoef(x, y)
print(z)
# [[1. 0.48510096]
# [0.48510096 1. ]]a = np.dot(x - np.mean(x), y - np.mean(y))
b = np.sqrt(np.dot(x - np.mean(x), x - np.mean(x)))
c = np.sqrt(np.dot(y - np.mean(y), y - np.mean(y)))
print(a / (b * c)) # 0.4851009629263671
直方图
numpy.digitize(x, bins, right=False)Return the indices of the bins to which each value in input array belongs.- x:numpy数组
- bins:一维单调数组,必须是升序或者降序
- right:间隔是否包含最右
- 返回值:x在bins中的位置。
【例】
import numpy as npx = np.array([0.2, 6.4, 3.0, 1.6])
bins = np.array([0.0, 1.0, 2.5, 4.0, 10.0])
inds = np.digitize(x, bins)
print(inds) # [1 4 3 2]
for n in range(x.size):print(bins[inds[n] - 1], "<=", x[n], "<", bins[inds[n]])# 0.0 <= 0.2 < 1.0
# 4.0 <= 6.4 < 10.0
# 2.5 <= 3.0 < 4.0
# 1.0 <= 1.6 < 2.5
【例】
import numpy as npx = np.array([1.2, 10.0, 12.4, 15.5, 20.])
bins = np.array([0, 5, 10, 15, 20])
inds = np.digitize(x, bins, right=True)
print(inds) # [1 2 3 4 4]inds = np.digitize(x, bins, right=False)
print(inds) # [1 3 3 4 5]
当前活动
我是 终身学习者“老马”,一个长期践行“结伴式学习”理念的 中年大叔。
我崇尚分享,渴望成长,于2010年创立了“LSGO软件技术团队”,并加入了国内著名的开源组织“Datawhale”,也是“Dre@mtech”、“智能机器人研究中心”和“大数据与哲学社会科学实验室”的一员。
愿我们一起学习,一起进步,相互陪伴,共同成长。
后台回复「搜搜搜」,随机获取电子资源!
欢迎关注,请扫描二维码:

相关文章:
Windows 7+Code::Blocks+wxWidgets实录(一)
环境配置篇 玩过Linux的人应该对Code::Blocks和wxWidgets并不陌生。 Code::Blocks是一款非常有名的代码编辑器,在linux下用不惯vim的话,这是个不错的选择。但千万不要把它和编译器混淆,CB本身并没有独立编译程序的功能,需要调用系…

技巧:两部解决U盘安装windows 7
第一步:准备一个4G的U盘并使用disk part 工具制作成引导盘1、在运行中输入cmd 回车2、在黑色的命令提示符界面中输入Diskpart3、插入U盘 并输入List Disk查看4、输入Select Disk 1 (选择你的U盘所在的标识)5、输入clean 清除旧的信息6、输入c…

报Java面授班有哪些优势
java技术在互联网行业的高速发展,让很多人都开始学习java技术,大家都想知道学习java技术面授班好还是网络班好,小编觉得当然是面授班比较好,下面小编就带大家来详细的了解一下报Java面授班有哪些优势? 报Java面授班有哪…

刻意练习:Python基础 -- Task13. datetime模块详解
datetime模块 datetime 是 Python 中处理日期的标准模块,它提供了 4 种对日期和时间进行处理的类:datetime、date、time 和 timedelta。 datetime类 class datetime(date):def __init__(self, year, month, day, hour, minute, second, microsecond, t…

关于java和c的选择结构和循环结构
java和c在这些结构上确实没区别。 另学会一个小技巧,在编辑界面选中段落之后按tab可以整体后移选中的段落,再按shifttab可以将选中的段落前移。转载于:https://www.cnblogs.com/hloli/archive/2012/03/15/2398675.html

从控制器到驱动器的WD——硬盘巨头启示录之西数篇
WD(Western Digital,西部数据)公司创立的时间比希捷公司还早近10年,但作为硬盘驱动器供应商的历史可不算长。1970年4月23日,一家名为General Digital(通用数字)的公司诞生了,其最初是…

java程序员入门先学什么开发者工具
学习java编程语言,那么开发工具是肯定少不了的,程序员入门基础中开发工具是一定要学会的,可以帮助开发者们提高开发效率、更优雅的写代码。由于开发者涉及的技术领域众多,以后端开发者的视角盘点平时可能用得到的工具,…

Numpy入门教程:11. 时间日期和时间增量
序言 什么是 NumPy 呢? NumPy 这个词来源于两个单词 – Numerical和Python。其是一个功能强大的 Python 库,可以帮助程序员轻松地进行数值计算,通常应用于以下场景: 执行各种数学任务,如:数值积分、微分、…

C#事件的发送方和接收方(订阅方)
C#事件的发送方和接收方(订阅方)基于Windows的应用程序也是基于消息的,Windows使用预定义消息与应用程序通讯。.NET Framework将Windows消息封装在事件中,可以把事件作为对象之间的通讯介质。事件发送方:发送事件的对象…

后台管理界面模版
http://www.cssmoban.com/cssthemes/houtaimoban/index_3.shtml转载于:https://www.cnblogs.com/hellojesson/p/7805516.html

选择PMP培训学校需要注意哪些
选择PMP培训学校需要注意哪些?如今各大职场对于项目管理这个岗位都是非常有需求的,有需求就有市场,PMP培训相关证书在市面上频繁出现,想要选择PMP培训学校需要注意哪些呢?来看看下面的详细介绍。 首先,我们来详细的了解一下什么…

绝对实用 NAT + VLAN +ACL管理企业网络
在企业中,要实现所有的员工都能与互联网进行通信,每个人各使用一个公网地址是很不现实的。一般,企业有1个或几个公网地址,而企业有几十、几百个员工。要想让所有的员工使用这仅有的几个公网地址与互联网通信该怎么做呢?…

javascript 常用功能總結
1.路径符号的含义 src"/js/jquery.js"、"../"这个斜杠是绝对路径的意思,表示的是网站根目录. 其他的如"./ " 、 "../" 、 "jquery.js" 、 "js/jquery.js"等等表示的都是相对当前网页的路径,…
学习资源:在线学习 Python(一)
背景 Python 是一种通用编程语言,其在科学计算和机器学习领域具有广泛的应用。如果我们打算利用 Python 来执行机器学习的代码,那么对 Python 有一些基本的了解就是至关重要的。 如果我们希望熟悉 Python 基本语法结构,但不希望在本地安装I…

什么BRIEF算法?BRIEF算法详解
BRIEF是一种特征描述子提取算法,并非特征点的提取算法,一种生成二值化描述子的算法,不提取代价低,匹配只需要使用简单的汉明距离(Hamming Distance)利用比特之间的异或操作就可以完成。因此,时间代价低,空间…

OpenLayers 动态添加标记(Marker)和信息窗(Popup)
方式一:使用marker方式 1、在地图上添加标记图层 var markers newOpenLayers.Layer.Markers("Markers"); map.addLayer(markers);//地图初始化添加 2、动态添加标记和Popup方法: //add map initial methodmap.events.register(click, this, fu…

Bag标签之中的一个行代码实行中文分词实例2
例1: 分词(返回以逗号隔开每一个词带上引號的词组。gap",",quotes""或quotes") 单引號 <bag idpPage act2words namewords gap"," quotes"">我喜欢黄色高领T恤衫</bag>…
学习资源:在线学习 Python(二)
背景 Python 是一种通用编程语言,其在科学计算和机器学习领域具有广泛的应用。如果我们打算利用 Python 来执行机器学习的代码,那么对 Python 有一些基本的了解就是至关重要的。 如果我们希望熟悉 Python 基本语法结构,但不希望在本地安装I…

Java培训完可以应用在什么领域
java技术在互联网行业一直都是非常有发展前景的,很多小伙伴都想知道“Java培训完可以应用在什么领域”这个问题,下面小编就来为大家做下详细的介绍。 Java培训完可以应用在什么领域?java的应用非常的广泛,可以用来在开发软件工具、嵌入式…

技术图文:Matlab VS. Numpy 矩阵基本运算
背景 前段时间在知识星球上立了一个Flag,至少写10篇关于 Python,Matlab 和 C# 对比的总结。 这是第 3 篇,对比 Matlab 与 Numpy 在矩阵基本运算方面的区别与联系。 虽然 Numpy 定义了 matrix 类型,使用该 matrix 类型创建的是矩…
Improve Performance and Reduce Memory with PVRTC Textures and Cocos2d
转载自:http://www.uchidacoonga.com/2011/07/pvrtc-textures-and-cocos2d/ Hello everyone! A few months have passed since I posted Simple Platformer Using Cocos2d and Box2d with Collision Detection. I have received many positive feedbacks and intere…

VDI序曲二十三 制作OFFICE 2003应用程序虚拟化序列
APP-V平台由三个重要组件构成:APP-V排序器、用于虚拟应用程序交付和管理的APP-V管理和流式处理服务器以及APP-V客户端。并且在虚拟环境中不会包含不必要的文件和设置,让IT管理员按需交付应用程序软件。 我们之前在一台干净的PC上做好了“捕获鸟笼”&…

零基础学Java程序有什么好的建议
java技术的快速发展,引起了很多人的关注,尤其是一些零基础人群,都想通过学习java技术来改善自己的职业,那么零基础学Java程序有什么好的建议呢?来看看下面的详细介绍。 零基础学Java程序有什么好的建议? 1.选择对的书籍…

Numpy入门教程:12. 线性代数
背景 什么是 NumPy 呢? NumPy 这个词来源于两个单词 – Numerical和Python。其是一个功能强大的 Python 库,可以帮助程序员轻松地进行数值计算,通常应用于以下场景: 执行各种数学任务,如:数值积分、微分、…
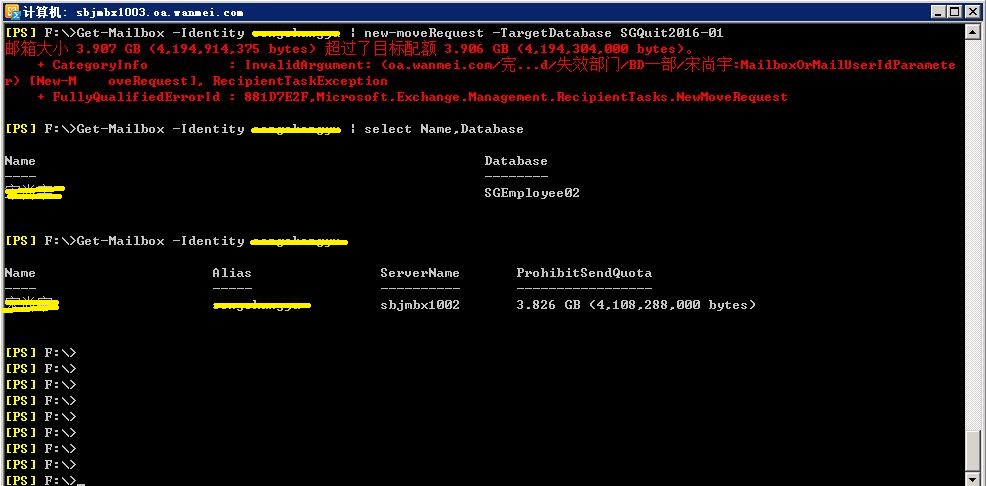
Exchange 2010 移动邮箱时提示超过了目标配额
在使用 new-moveRequest 移动邮箱时,提示超过了目标配额。解决过程如下: 经查看,此邮箱配额为 3.826G ,由于邮箱实际比配额大,因此移动时出现下面的错误 找到该用户,邮箱设置-存储配额,最下面的…

什么是URL?协议头,路径和端口是什么意思?
URL(Uniform Resource Locator,统一资源定位符)是互联网上标准资源的地址,互联网上每个文件(即资源)都有一个唯一的URL,它包含了文件的位置以及浏览器处理方式等信息。 URL地址由协议头、服务器地址、文件路径三部分组成。比如,一…

技术图文:Matlab VS. Numpy 常见矩阵
背景 前段时间在知识星球上立了一个Flag,至少写10篇关于 Python,Matlab 和 C# 对比的总结。 这是第 4 篇,对比 Matlab 与 Numpy 中经常用到的各种矩阵,比如零矩阵、单位矩阵、全1矩阵、对角矩阵、均匀分布的随机矩阵、标准正态分…

CssGaga 快速上手指南
CssGaga是ytzong(涛哥)基于我们在朋友网日常的重构工作流程,为了提高工作效率而开发并不断完善起来的一个重构辅助工具。运行于Windows .NET的环境,提供了重构相关的一系列解决方案。最近越来越多的朋友通过腾讯微博、QQ和Email咨…

学习web前端开发要注意什么
web前端的发展前景有目共睹,越来越多的人都对web前端这门编程语言非常感兴趣,想要学习web前端技术,那么学习web前端开发要注意什么呢?大家在学习之前是否有做好这些功课呢?来看看下面的详细介绍吧。 学习web前端开发要注意什么? 1、任何技…

Nagios之事件处理
目标:实现在监控3306端口服务时,出现1次critical软状态时或者在上一次执行后没有成功后出现的第一次硬状态critical情况下,远程执行mysql重启服务,并且每次执行远程重启服务前把报告事件记录到DB中 牵涉技术: (1)Nagios事件处理原理 (2)Ssh无…
