Numpy入门教程:12. 线性代数
背景
什么是 NumPy 呢?
NumPy 这个词来源于两个单词 – Numerical和Python。其是一个功能强大的 Python 库,可以帮助程序员轻松地进行数值计算,通常应用于以下场景:
- 执行各种数学任务,如:数值积分、微分、内插、外推等。因此,当涉及到数学任务时,它形成了一种基于 Python 的 MATLAB 的快速替代。
- 计算机中的图像表示为多维数字数组。NumPy 提供了一些优秀的库函数来快速处理图像。例如,镜像图像、按特定角度旋转图像等。
- 在编写机器学习算法时,需要对矩阵进行各种数值计算。如:矩阵乘法、求逆、换位、加法等。NumPy 数组用于存储训练数据和机器学习模型的参数。
线性代数
Numpy 定义了 matrix 类型,使用该 matrix 类型创建的是矩阵对象,它们的加减乘除运算缺省采用矩阵方式计算,因此用法和Matlab十分类似。但是由于 NumPy 中同时存在 ndarray 和 matrix 对象,因此用户很容易将两者弄混。这有违 Python 的“显式优于隐式”的原则,因此官方并不推荐在程序中使用 matrix。在这里,我们仍然用 ndarray 来介绍。
矩阵和向量积
矩阵的定义、矩阵的加法、矩阵的数乘、矩阵的转置与二维数组完全一致,不再进行说明,但矩阵的乘法有不同的表示。
numpy.dot(a, b[, out])计算两个矩阵的乘积,如果是一维数组则是它们的内积。
【例1】
import numpy as npx = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 5, 6])
z = np.dot(x, y)
print(z) # 70x = np.array([[1, 2, 3], [3, 4, 5], [6, 7, 8]])
print(x)
# [[1 2 3]
# [3 4 5]
# [6 7 8]]y = np.array([[5, 4, 2], [1, 7, 9], [0, 4, 5]])
print(y)
# [[5 4 2]
# [1 7 9]
# [0 4 5]]z = np.dot(x, y)
print(z)
# [[ 7 30 35]
# [ 19 60 67]
# [ 37 105 115]]z = np.dot(y, x)
print(z)
# [[ 29 40 51]
# [ 76 93 110]
# [ 42 51 60]]
注意:在线性代数里面讲的维数和数组的维数不同,如线代中提到的n维行向量在 Numpy 中是一维数组,而线性代数中的n维列向量在 Numpy 中是一个shape为(n, 1)的二维数组。
矩阵特征值与特征向量
numpy.linalg.eig(a)计算方阵的特征值和特征向量。numpy.linalg.eigvals(a)计算方阵的特征值。
【例1】求方阵的特征值特征向量
import numpy as np# 创建一个对角矩阵!
x = np.diag((1, 2, 3))
print(x)
# [[1 0 0]
# [0 2 0]
# [0 0 3]]print(np.linalg.eigvals(x))
# [1. 2. 3.]a, b = np.linalg.eig(x)
# 特征值保存在a中,特征向量保存在b中
print(a)
# [1. 2. 3.]
print(b)
# [[1. 0. 0.]
# [0. 1. 0.]
# [0. 0. 1.]]# 检验特征值与特征向量是否正确
for i in range(3): if np.allclose(a[i] * b[:, i], np.dot(x, b[:, i])):print('Right')else:print('Error')
# Right
# Right
# Right
【例2】判断对称阵是否为正定阵(特征值是否全部为正)。
import numpy as npA = np.arange(16).reshape(4, 4)
print(A)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]
# [12 13 14 15]]A = A + A.T # 将方阵转换成对称阵
print(A)
# [[ 0 5 10 15]
# [ 5 10 15 20]
# [10 15 20 25]
# [15 20 25 30]]B = np.linalg.eigvals(A) # 求A的特征值
print(B)
# [ 6.74165739e+01 -7.41657387e+00 1.82694656e-15 -1.72637110e-15]# 判断是不是所有的特征值都大于0,用到了all函数,显然对称阵A不是正定的
if np.all(B > 0):print('Yes')
else:print('No')
# No
矩阵分解
奇异值分解
有关奇异值分解的原理:奇异值分解(SVD)及其应用
u, s, v = numpy.linalg.svd(a, full_matrices=True, compute_uv=True, hermitian=False)奇异值分解a是一个形如(M,N)矩阵full_matrices的取值是为False或者True,默认值为True,这时u的大小为(M,M),v的大小为(N,N)。否则u的大小为(M,K),v的大小为(K,N) ,K=min(M,N)。compute_uv的取值是为False或者True,默认值为True,表示计算u,s,v。为False的时候只计算s。- 总共有三个返回值
u,s,v,u大小为(M,M),s大小为(M,N),v大小为(N,N),a = u*s*v。 - 其中
s是对矩阵a的奇异值分解。s除了对角元素不为0,其他元素都为0,并且对角元素从大到小排列。s中有n个奇异值,一般排在后面的比较接近0,所以仅保留比较大的r个奇异值。
注:Numpy中返回的v是通常所谓奇异值分解a=u*s*v'中v的转置。
【例1】
import numpy as npA = np.array([[4, 11, 14], [8, 7, -2]])
print(A)
# [[ 4 11 14]
# [ 8 7 -2]]u, s, vh = np.linalg.svd(A, full_matrices=False)
print(u.shape) # (2, 2)
print(u)
# [[-0.9486833 -0.31622777]
# [-0.31622777 0.9486833 ]]print(s.shape) # (2,)
print(np.diag(s))
# [[18.97366596 0. ]
# [ 0. 9.48683298]]print(vh.shape) # (2, 3)
print(vh)
# [[-0.33333333 -0.66666667 -0.66666667]
# [ 0.66666667 0.33333333 -0.66666667]]a = np.dot(u, np.diag(s))
a = np.dot(a, vh)
print(a)
# [[ 4. 11. 14.]
# [ 8. 7. -2.]]
【例2】
import numpy as npA = np.array([[1, 1], [1, -2], [2, 1]])
print(A)
# [[ 1 1]
# [ 1 -2]
# [ 2 1]]u, s, vh = np.linalg.svd(A, full_matrices=False)
print(u.shape) # (3, 2)
print(u)
# [[-5.34522484e-01 -1.11022302e-16]
# [ 2.67261242e-01 -9.48683298e-01]
# [-8.01783726e-01 -3.16227766e-01]]print(s.shape) # (2,)
print(np.diag(s))
# [[2.64575131 0. ]
# [0. 2.23606798]]print(vh.shape) # (2, 2)
print(vh)
# [[-0.70710678 -0.70710678]
# [-0.70710678 0.70710678]]a = np.dot(u, np.diag(s))
a = np.dot(a, vh)
print(a)
# [[ 1. 1.]
# [ 1. -2.]
# [ 2. 1.]]
QR分解
q,r = numpy.linalg.qr(a, mode='reduced')计算矩阵a的QR分解。a是一个(M, N)的待分解矩阵。mode = reduced:返回(M, N)的列向量两两正交的矩阵q,和(N, N)的三角阵r(Reduced QR分解)。mode = complete:返回(M, M)的正交矩阵q,和(M, N)的三角阵r(Full QR分解)。
【例1】
import numpy as npA = np.array([[2, -2, 3], [1, 1, 1], [1, 3, -1]])
print(A)
# [[ 2 -2 3]
# [ 1 1 1]
# [ 1 3 -1]]q, r = np.linalg.qr(A)
print(q.shape) # (3, 3)
print(q)
# [[-0.81649658 0.53452248 0.21821789]
# [-0.40824829 -0.26726124 -0.87287156]
# [-0.40824829 -0.80178373 0.43643578]]print(r.shape) # (3, 3)
print(r)
# [[-2.44948974 0. -2.44948974]
# [ 0. -3.74165739 2.13808994]
# [ 0. 0. -0.65465367]]print(np.dot(q, r))
# [[ 2. -2. 3.]
# [ 1. 1. 1.]
# [ 1. 3. -1.]]a = np.allclose(np.dot(q.T, q), np.eye(3))
print(a) # True
【例2】
import numpy as npA = np.array([[1, 1], [1, -2], [2, 1]])
print(A)
# [[ 1 1]
# [ 1 -2]
# [ 2 1]]q, r = np.linalg.qr(A, mode='complete')
print(q.shape) # (3, 3)
print(q)
# [[-0.40824829 0.34503278 -0.84515425]
# [-0.40824829 -0.89708523 -0.16903085]
# [-0.81649658 0.27602622 0.50709255]]print(r.shape) # (3, 2)
print(r)
# [[-2.44948974 -0.40824829]
# [ 0. 2.41522946]
# [ 0. 0. ]]print(np.dot(q, r))
# [[ 1. 1.]
# [ 1. -2.]
# [ 2. 1.]]a = np.allclose(np.dot(q, q.T), np.eye(3))
print(a) # True
【例3】
import numpy as npA = np.array([[1, 1], [1, -2], [2, 1]])
print(A)
# [[ 1 1]
# [ 1 -2]
# [ 2 1]]q, r = np.linalg.qr(A)
print(q.shape) # (3, 2)
print(q)
# [[-0.40824829 0.34503278]
# [-0.40824829 -0.89708523]
# [-0.81649658 0.27602622]]print(r.shape) # (2, 2)
print(r)
# [[-2.44948974 -0.40824829]
# [ 0. 2.41522946]]print(np.dot(q, r))
# [[ 1. 1.]
# [ 1. -2.]
# [ 2. 1.]]a = np.allclose(np.dot(q.T, q), np.eye(2))
print(a) # True
Cholesky分解
L = numpy.linalg.cholesky(a)返回正定矩阵a的 Cholesky 分解a = L*L.H,其中L是下三角。
【例1】
import numpy as npA = np.array([[1, 1, 1, 1], [1, 3, 3, 3],[1, 3, 5, 5], [1, 3, 5, 7]])
print(A)
# [[1 1 1 1]
# [1 3 3 3]
# [1 3 5 5]
# [1 3 5 7]]print(np.linalg.eigvals(A))
# [13.13707118 1.6199144 0.51978306 0.72323135]L = np.linalg.cholesky(A)
print(L)
# [[1. 0. 0. 0. ]
# [1. 1.41421356 0. 0. ]
# [1. 1.41421356 1.41421356 0. ]
# [1. 1.41421356 1.41421356 1.41421356]]print(np.dot(L, L.T))
# [[1. 1. 1. 1.]
# [1. 3. 3. 3.]
# [1. 3. 5. 5.]
# [1. 3. 5. 7.]]
范数和其它数字
矩阵的范数
numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)计算向量或者矩阵的范数。
根据ord参数的不同,计算不同的范数:
| ord | 向量的范数 | 矩阵的范数 |
|---|---|---|
| 1 | sum(abs(x)**ord)**(1./ord) | max(sum(abs(A), axis=0)) |
| 2 | sum(abs(x)**ord)**(1./ord) | max(svd(A)) |
-np.inf | max(abs(x)) | - |
np.inf | min(abs(x)) | max(sum(abs(A), axis=1)) |
| ‘fro’ | - | sqrt(trace(dot(A.T,A))) |
【例1】求向量的范数。
import numpy as npx = np.array([1, 2, 3, 4])print(np.linalg.norm(x, ord=1))
# 10.0
print(np.sum(np.abs(x)))
# 10print(np.linalg.norm(x, ord=2))
# 5.477225575051661
print(np.sum(np.abs(x) ** 2) ** 0.5)
# 5.477225575051661print(np.linalg.norm(x, ord=-np.inf))
# 1.0
print(np.min(np.abs(x)))
# 1print(np.linalg.norm(x, ord=np.inf))
# 4.0
print(np.max(np.abs(x)))
# 4
【例2】求矩阵的范数
import numpy as npA = np.array([[1, 2, 3, 4], [2, 3, 5, 8],[1, 3, 5, 7], [3, 4, 7, 11]])print(A)
# [[ 1 2 3 4]
# [ 2 3 5 8]
# [ 1 3 5 7]
# [ 3 4 7 11]]print(np.linalg.norm(A, ord=1)) # 30.0
print(np.max(np.sum(A, axis=0))) # 30print(np.linalg.norm(A, ord=2))
# 20.24345358700576
print(np.max(np.linalg.svd(A, compute_uv=False)))
# 20.24345358700576print(np.linalg.norm(A, ord=np.inf)) # 25.0
print(np.max(np.sum(A, axis=1))) # 25print(np.linalg.norm(A, ord='fro'))
# 20.273134932713294
print(np.sqrt(np.trace(np.dot(A.T, A))))
# 20.273134932713294
方阵的行列式
numpy.linalg.det(a)计算行列式。
【例】计算行列式。
import numpy as npx = np.array([[1, 2], [3, 4]])
print(x)
# [[1 2]
# [3 4]]print(np.linalg.det(x))
# -2.0000000000000004
矩阵的秩
numpy.linalg.matrix_rank(M, tol=None, hermitian=False)返回矩阵的秩。
【例】计算矩阵的秩。
import numpy as npI = np.eye(3) # 先创建一个单位阵
print(I)
# [[1. 0. 0.]
# [0. 1. 0.]
# [0. 0. 1.]]r = np.linalg.matrix_rank(I)
print(r) # 3I[1, 1] = 0 # 将该元素置为0
print(I)
# [[1. 0. 0.]
# [0. 0. 0.]
# [0. 0. 1.]]r = np.linalg.matrix_rank(I) # 此时秩变成2
print(r) # 2
矩阵的迹
numpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)方阵的迹就是主对角元素之和。
【例】计算方阵的迹。
import numpy as npx = np.array([[1, 2, 3], [3, 4, 5], [6, 7, 8]])
print(x)
# [[1 2 3]
# [3 4 5]
# [6 7 8]]y = np.array([[5, 4, 2], [1, 7, 9], [0, 4, 5]])
print(y)
# [[5 4 2]
# [1 7 9]
# [0 4 5]]print(np.trace(x)) # A的迹等于A.T的迹
# 13
print(np.trace(np.transpose(x)))
# 13print(np.trace(x + y)) # 和的迹 等于 迹的和
# 30
print(np.trace(x) + np.trace(y))
# 30
解方程和逆矩阵
逆矩阵(inverse matrix)
设 A 是数域上的一个 n 阶矩阵,若在相同数域上存在另一个 n 阶矩阵 B,使得:AB=BA=E(E 为单位矩阵),则我们称 B 是 A 的逆矩阵,而 A 则被称为可逆矩阵。
numpy.linalg.inv(a)计算矩阵a的逆矩阵(矩阵可逆的充要条件:det(a) != 0,或者a满秩)。
【例】计算矩阵的逆矩阵。
import numpy as npA = np.array([[1, -2, 1], [0, 2, -1], [1, 1, -2]])
print(A)
# [[ 1 -2 1]
# [ 0 2 -1]
# [ 1 1 -2]]# 求A的行列式,不为零则存在逆矩阵
A_det = np.linalg.det(A)
print(A_det)
# -2.9999999999999996A_inverse = np.linalg.inv(A) # 求A的逆矩阵
print(A_inverse)
# [[ 1.00000000e+00 1.00000000e+00 -1.11022302e-16]
# [ 3.33333333e-01 1.00000000e+00 -3.33333333e-01]
# [ 6.66666667e-01 1.00000000e+00 -6.66666667e-01]]x = np.allclose(np.dot(A, A_inverse), np.eye(3))
print(x) # True
x = np.allclose(np.dot(A_inverse, A), np.eye(3))
print(x) # TrueA_companion = A_inverse * A_det # 求A的伴随矩阵
print(A_companion)
# [[-3.00000000e+00 -3.00000000e+00 3.33066907e-16]
# [-1.00000000e+00 -3.00000000e+00 1.00000000e+00]
# [-2.00000000e+00 -3.00000000e+00 2.00000000e+00]]
求解线性方程组
numpy.linalg.solve(a, b)求解线性方程组或矩阵方程。
【例】求解线性矩阵方程
# x + 2y + z = 7
# 2x - y + 3z = 7
# 3x + y + 2z =18import numpy as npA = np.array([[1, 2, 1], [2, -1, 3], [3, 1, 2]])
b = np.array([7, 7, 18])
x = np.linalg.solve(A, b)
print(x) # [ 7. 1. -2.]x = np.linalg.inv(A).dot(b)
print(x) # [ 7. 1. -2.]y = np.allclose(np.dot(A, x), b)
print(y) # True
参考文献
- https://www.cnblogs.com/moon1992/p/4960700.html
- https://www.cnblogs.com/moon1992/p/4948793.html
后台回复「搜搜搜」,随机获取电子资源!
欢迎关注,请扫描二维码:


相关文章:
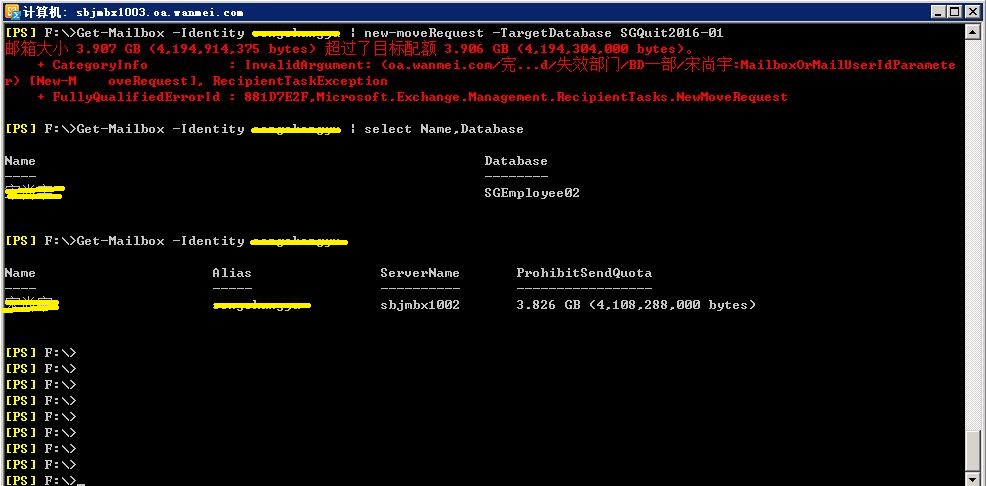
Exchange 2010 移动邮箱时提示超过了目标配额
在使用 new-moveRequest 移动邮箱时,提示超过了目标配额。解决过程如下: 经查看,此邮箱配额为 3.826G ,由于邮箱实际比配额大,因此移动时出现下面的错误 找到该用户,邮箱设置-存储配额,最下面的…

什么是URL?协议头,路径和端口是什么意思?
URL(Uniform Resource Locator,统一资源定位符)是互联网上标准资源的地址,互联网上每个文件(即资源)都有一个唯一的URL,它包含了文件的位置以及浏览器处理方式等信息。 URL地址由协议头、服务器地址、文件路径三部分组成。比如,一…

技术图文:Matlab VS. Numpy 常见矩阵
背景 前段时间在知识星球上立了一个Flag,至少写10篇关于 Python,Matlab 和 C# 对比的总结。 这是第 4 篇,对比 Matlab 与 Numpy 中经常用到的各种矩阵,比如零矩阵、单位矩阵、全1矩阵、对角矩阵、均匀分布的随机矩阵、标准正态分…

CssGaga 快速上手指南
CssGaga是ytzong(涛哥)基于我们在朋友网日常的重构工作流程,为了提高工作效率而开发并不断完善起来的一个重构辅助工具。运行于Windows .NET的环境,提供了重构相关的一系列解决方案。最近越来越多的朋友通过腾讯微博、QQ和Email咨…

学习web前端开发要注意什么
web前端的发展前景有目共睹,越来越多的人都对web前端这门编程语言非常感兴趣,想要学习web前端技术,那么学习web前端开发要注意什么呢?大家在学习之前是否有做好这些功课呢?来看看下面的详细介绍吧。 学习web前端开发要注意什么? 1、任何技…

Nagios之事件处理
目标:实现在监控3306端口服务时,出现1次critical软状态时或者在上一次执行后没有成功后出现的第一次硬状态critical情况下,远程执行mysql重启服务,并且每次执行远程重启服务前把报告事件记录到DB中 牵涉技术: (1)Nagios事件处理原理 (2)Ssh无…

张孝祥javascript学习笔记1---HTMLCSS
本节摘要及说明:本节只是对学习过程中知识点的一个简单的记录。 <body>标签的属性 Text属性:用于设定整个网页中的文字颜色 link属性:用于设定一般超链接文本的显示颜色 alink属性:用于设定鼠标移动到超链接上时,超链接文本的显示颜色 …
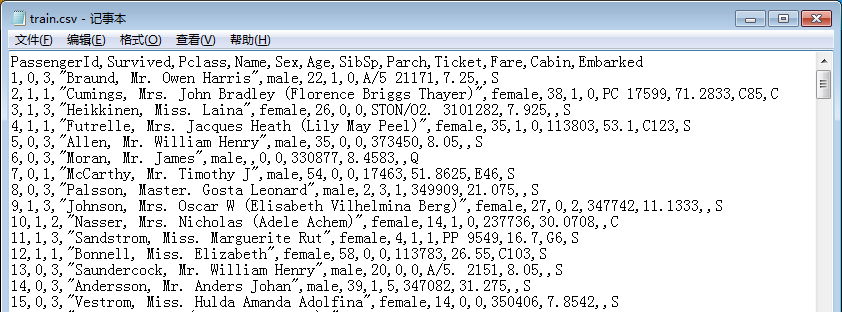
技术图文:C# VS. Python 读取CSV文件指南
背景 CSV 是一种以逗号进行特征分隔的文本文件类型,在数据库或电子表格中是一种非常常见的导入导出格式。本篇图文就以泰坦尼克号船员获救预测( Kaggle)中使用的数据集为例来说明 C#、Python和Pandas 如何读取 CSV 数据的。 CSV原始文件如下…
零基础学软件测试去哪家培训机构好
移动互联网的时代,几乎每个人都是机不离手,手机软件的应用频率越来越高,软件测试这个岗位的发展前景更是非常可观,很多人都开始学习软测技术,想要知道零基础学软件测试去哪家培训机构好?来看看下面的详细介绍。 零基础…

技术图文:Numpy 一维数组 VS. Pandas Series
背景 Numpy 提供的最重要的数据结构是 ndarray,它是 Python 中 list 的扩展。 Pandas 提供了两种非常重要的数据结构 Series和DataFrame。 Numpy 中的一维数组与 Series 相似,一维数组只是提供了从0开始与位置有关的索引,而Series除了位置…

【Python】向函数传递任意数量的实参
传递任意数量的实参 有时候,你预先不知道函数需要接受多少个实参,好在Python允许函数从调用语句中收集任意数量的实参 def get_letter(*letters):for i in letters:print(i) get_letter(A,B,C,D,E)形参名*letters中的星号让Python创建一个名为letters的空…

word中插入下标
Word2007中为数字加上下标的几种方法: 一:通过插入>公式>>选择,通过此上下标。 二:写下数字,例如5,然后按ctrlshift号三个键,就可添加上标,按ctrl号两键,就可标…

手机应用软件测试的思路与要点
软件测试主要针对于移动互联网行业,那么APP等相关软件的测试工作是非常多的,尤其对于产品的手机项目(应用软件),主要是进行系统测试。针对手机应用软件的系统测试,通常从如下几个角度开展:功能测试,兼容性测…
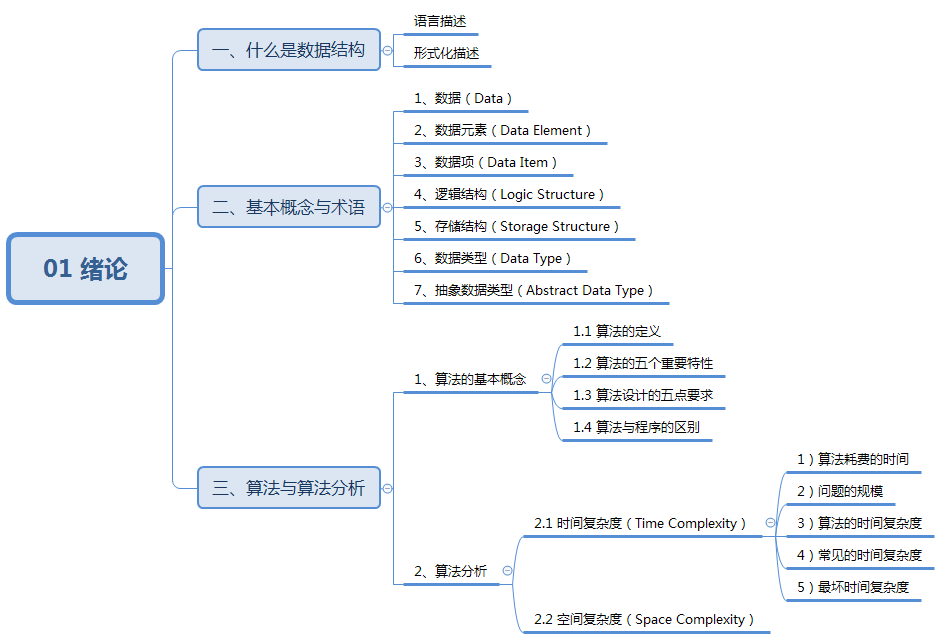
数据结构与算法:01 绪论
绪论 知识结构: 一、什么是数据结构 例1:电话号码薄的查询问题。 (a1,b1),(a2,b2),…,(an,bn)(a_1,b_1),(a_2,b_2),\dots,(a_n,b_n) (a1,b1),(a2,b2),…,(an,bn) aia_iai:表示姓名,bib_ibi:表示电话…

rar for linux缺少GLIBC_2.7
今天安装rar4.0 for linux,遇到了一个缺少GLIBC_2.7的问题,弄了好久才成功,记录一下,以备不时之需。 系统版本为CentOS 5.5。下载了rar4.0 for linux源码包,解压后,按照makfile文件的提示,进行安…

硅谷产学研的创新循环
在现代社会形态形成的几百年历史中,大学与产业界在分化的体制轨道中形成了各自不同的目标、结构和文化,有关大学与产业合作的种种争议无不缘自于此。今天当知识和技术逐步取代了自然资源和简单劳动力资源而成为首要的创造财富的源泉时,产业界…
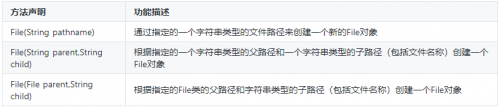
java技术培训之File类中常用的构造方法
File类用于封装一个路径,这个路径可以是从系统盘符开始的绝对路径,如:“D:\file\a.txt”,也可以是相对于当前目录而言的相对路径,如:“src\Hello.java”。File类内部封装的路径可以指向一个文件,…

数据结构与算法:02 C#语言基本语法结构
02 C#语言基本语法结构 知识结构: 1、数据类型 第一种分类: 简单数据类型:byte、short、int、long、float、double、char、bool组合数据类型:struct、enum、class、interface 类型描述byte无符号8位整型(ushort) short&#x…

积少成多 Flash(ActionScript 3.0 Flex 3.0) 系列文章索引
[源码下载]积少成多 Flash(ActionScript 3.0 & Flex 3.0) 系列文章索引作者:webabcdFlash 之 ActionScript 3.0 1、积少成多Flash(1) - ActionScript 3.0 基础之数据类型、操作符和流程控制语句介绍Flash ActionScript 3.0 中所有的数据类型都是对象,…

WPF Snoop 2.7 源码研究
转载于:https://www.cnblogs.com/puncha/archive/2012/04/01/3877001.html

java培训基础知识都学哪些
很多人都开始学习java技术,觉得java语言在未来的发展前景空间非常大,事实却是如此,那么针对于零基础的同学, 学习java技术需要学哪些呢?下面我们就来看看java培训基础知识都学哪些? java培训基础知识都学哪些? 1.JavaWeb Linux…
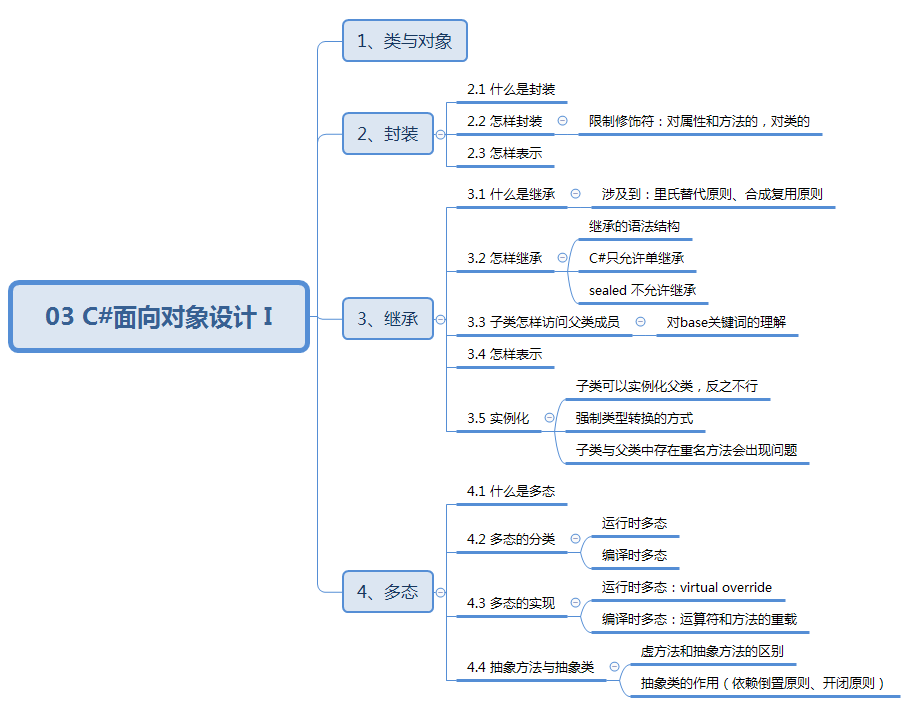
数据结构与算法:03 C#面向对象设计 I
03 C#面向对象设计 I 知识结构: 1、类与对象 类:用高级程序语言实现的一个ADT描述。对象:通过类声明的变量。 2、封装 2.1 什么是封装 把类的内部隐藏起来以防止外部看到内部的实现过程。 2.2 怎样封装 通过限制修饰符private、protect…

Centos7安装编译安装zabbix2.219及mariadb-5.5.46
mariadb-5.5.46的安装: 首先下载mariadb-5.5.46-linux-x86_64.tar.gz,然后使用tar -xf mariadb-5.5.46-linux-x86_64.tar.gz -C /usr/local目录下 添加数据库组 # groupadd mysql 添加数据库用户 # useradd -g mysql mysql cd /usr/local ln -sv…

软件测试开发:常见测试类型概念
软件测试是软件开发中非常重要的一个环节,软件测试工程师需要对每个环节进行严格把控,才能保证系统在每个阶段得以控制。下面小编就为大家详细介绍一下软件测试开发:常见测试类型概念的相关内容。 软件测试开发:常见测试类型概念: (1)边界测试…
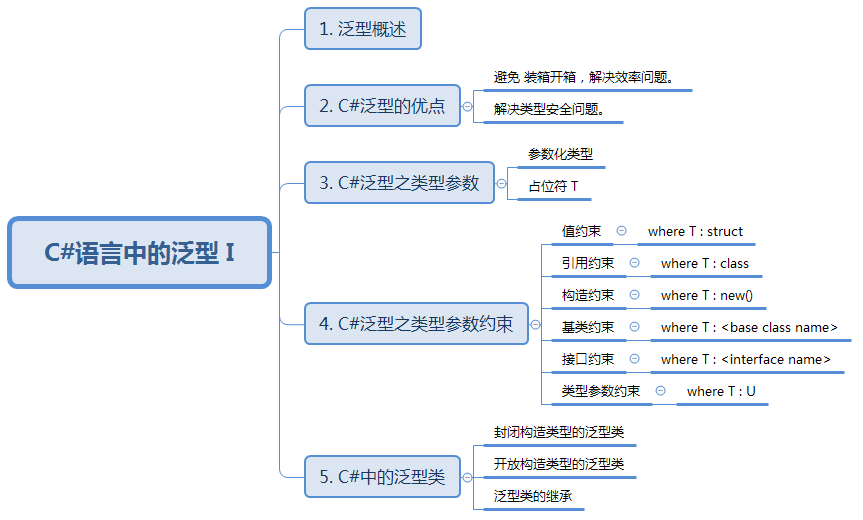
技术图文:C#语言中的泛型 I
C#语言中的泛型 I 知识结构: 1. 泛型概述 泛型广泛应用于容器(Collections)和对容器操作的方法中。 从 .NET Framework2.0 开始,微软提供了一个新的命名空间System.Collections.Generic,其中包含了一些新的基于泛型…

ubuntu搭建svn、git遇到的问题及解决办法
不错的git笔记博客: http://www.cnblogs.com/wanqieddy/category/406859.html http://blog.csdn.net/zxncvb/article/details/22153019 Git学习教程(六)Git日志 http://fsjoy.blog.51cto.com/318484/245261/ 图解git http://my.oschina.net/x…

webstorm同时打开多个project方法
曾经多次碰到过想要打开多个project的时候,可每次打开其他项目时,必须选择新窗口还是替换次窗口,如果新窗口的话就无法跟现在的项目在同一个webstorm中同时进行编辑,需要来回切换窗口,很是不方便,今天无意中…

什么业务场景适合使用Redis?
Redis(Remote Dictionary Server ),即远程字典服务,是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。从2010年3月15日起,Redis的开发工作由VMware主持。从2013年…

Linux基础知识汇总(2)...持续更新中
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566软件安装: {软件安装的几种形式 rpm 由厂商提供二进制包 yum rpm源的前端管理器 src 源码包configure安装 bin 包含rpm和shell将安装一步执…
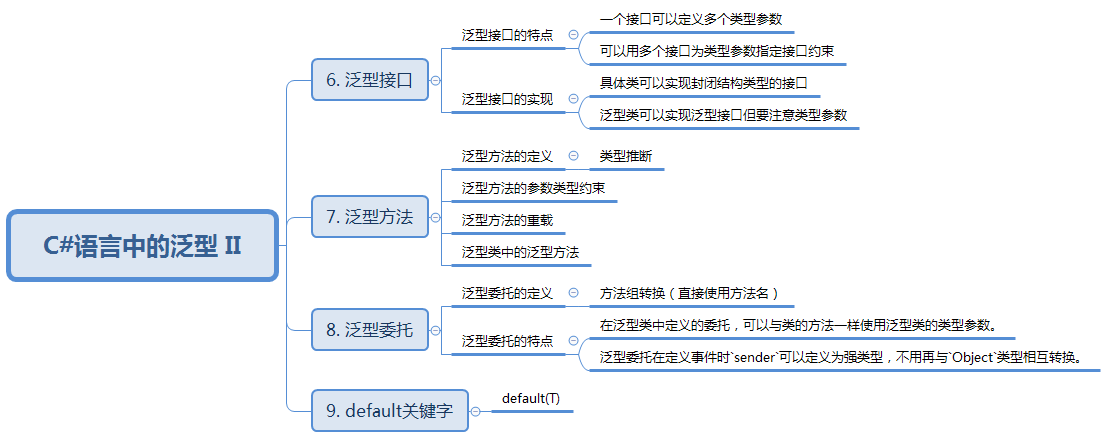
技术图文:C#语言中的泛型 II
C#语言中的泛型 II 知识结构: 6. 泛型接口 泛型类与泛型接口结合使用是很好的编程习惯,比如用IComparable<T>而非IComparable,以避免值类型上的装箱和拆箱操作。若将接口指定为类型参数的约束(接口约束)&#…
