当前位置：首页 > 编程日记 > 正文

用欧几里得算法求最大公约数_欧几里得算法：GCD（最大公约数），用C ++和Java示例解释...

编程日记 2024-08-02 11:10:00

用欧几里得算法求最大公约数

For this topic you must know about Greatest Common Divisor (GCD) and the MOD operation first.

对于本主题，您必须首先了解最大公约数(GCD)和MOD操作。

最大公约数(GCD) (Greatest Common Divisor (GCD))

The GCD of two or more integers is the largest integer that divides each of the integers such that their remainder is zero.

两个或多个整数的GCD是将每个整数相除以使它们的余数为零的最大整数。

Example-GCD of 20, 30 = 10 (10 is the largest number which divides 20 and 30 with remainder as 0)GCD of 42, 120, 285 = 3 (3 is the largest number which divides 42, 120 and 285 with remainder as 0)

Example-GCD为20、30 = 10 (10是将20和30除以0的最大数) ，42、120、285 = 3 (3是将42、120和285除以余数的最大数) 0)

“ mod”操作 ("mod" Operation)

The mod operation gives you the remainder when two positive integers are divided. We write it as follows-A mod B = R

当两个正整数相除时，mod操作为您提供余数。我们将其编写如下： A mod B = R

This means, dividing A by B gives you the remainder R, this is different than your division operation which gives you the quotient.

这意味着，用A除以B得到的余数为R，这与除以商的商不同。

Example-7 mod 2 = 1 (Dividing 7 by 2 gives the remainder 1)42 mod 7 = 0 (Dividing 42 by 7 gives the remainder 0)

示例7 mod 2 = 1 (将7除以2得到余数1) 42 mod 7 = 0 (将42除以7得到余数0)

With the above two concepts understood you will easily understand the Euclidean Algorithm.

了解了以上两个概念后，您将轻松理解欧几里得算法。

欧几里德最大公约数算法(GCD) (Euclidean Algorithm for Greatest Common Divisor (GCD))

The Euclidean Algorithm finds the GCD of 2 numbers.

欧几里得算法找到2个数字的GCD。

You will better understand this Algorithm by seeing it in action. Assuming you want to calculate the GCD of 1220 and 516, lets apply the Euclidean Algorithm-

通过查看实际效果，您将更好地理解该算法。假设您要计算1220和516的GCD，请应用欧几里得算法-

Assuming you want to calculate the GCD of 1220 and 516, lets apply the Euclidean Algorithm-

假设您要计算1220和516的GCD，请应用欧几里得算法-

Pseudo Code of the Algorithm-Step 1: Let a, b be the two numbersStep 2: a mod b = RStep 3: Let a = b and b = RStep 4: Repeat Steps 2 and 3 until a mod b is greater than 0Step 5: GCD = bStep 6: Finish

算法的伪代码-步骤1： 令a, b为两个数字步骤2： a mod b = R步骤3： 令a = b和b = R步骤4： 重复步骤2和3，直到a mod b更大大于0步骤5： GCD = b步骤6：完成

JavaScript Code to Perform GCD-

执行GCD-JavaScript代码

function gcd(a, b) {var R;while ((a % b) > 0)  {R = a % b;a = b;b = R;}return b;
}

JavaScript Code to Perform GCD using Recursion-

使用递归执行GCDJavaScript代码-

function gcd(a, b) {if (b == 0)return a;elsereturn gcd(b, (a % b));
}

C code to perform GCD using recursion

使用递归执行GCD的C代码

int gcd(int a, int b) 
{ // Everything divides 0  if (a == 0) return b; if (b == 0) return a; // base case if (a == b) return a; // a is greater if (a > b) return gcd(a-b, b); return gcd(a, b-a); 
}

C++ Code to Perform GCD-

执行GCD-的C ++代码

int gcd(int a,int b) {int R;while ((a % b) > 0)  {R = a % b;a = b;b = R;}return b;
}

Python Code to Perform GCD using Recursion

使用递归执行GCD的Python代码

def gcd(a, b):if b == 0:return a:else:return gcd(b, (a % b))

Java Code to Perform GCD using Recursion

Java代码使用递归执行GCD

static int gcd(int a, int b)
{if(b == 0){return a;}return gcd(b, a % b);
}

You can also use the Euclidean Algorithm to find GCD of more than two numbers. Since, GCD is associative, the following operation is valid- GCD(a,b,c) == GCD(GCD(a,b), c)

您也可以使用欧几里得算法来查找两个以上的GCD。由于GCD是关联的，因此以下操作有效-GCD GCD(a,b,c) == GCD(GCD(a,b), c)

Calculate the GCD of the first two numbers, then find GCD of the result and the next number. Example- GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7

计算前两个数字的GCD，然后找到结果和下一个数字的GCD。 GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7

You can find GCD of n numbers in the same way.

您可以用相同的方法找到n数字的GCD。

什么是扩展欧几里得算法？ (What is the Extended Euclidean Algorithm?)

This is an extension of Euclidean algorithm. It also calculates the coefficients x, y such that

这是欧几里得算法的扩展。它还计算系数x，y，这样

ax+by = gcd(a,b)

ax + by = gcd(a，b)

x and y are also known as coefficients of Bézout's identity.

x和y也称为贝索特恒等式的系数。

c code for Extended Euclidean algorithm

扩展欧几里得算法的C代码

struct Triplet{int gcd;int x;int y;
};
Triplet gcdExtendedEuclid(int a,int b){//Base Caseif(b==0){Triplet myAns;myAns.gcd = a;myAns.x = 1;myAns.y = 0;return myAns;}Triplet smallAns = gcdExtendedEuclid(b,a%b);//Extended euclid saysTriplet myAns;myAns.gcd = smallAns.gcd;myAns.x  = smallAns.y;myAns.y = (smallAns.x - ((a/b)*(smallAns.y)));return myAns;	
}

翻译自: https://www.freecodecamp.org/news/euclidian-gcd-algorithm-greatest-common-divisor/

用欧几里得算法求最大公约数

https://www.dkcj.cn/info/12486.html

用欧几里得算法求最大公约数_欧几里得算法：GCD（最大公约数），用C ++和Java示例解释...

最大公约数(GCD) (Greatest Common Divisor (GCD))

“ mod”操作 ("mod" Operation)

欧几里德最大公约数算法(GCD) (Euclidean Algorithm for Greatest Common Divisor (GCD))

什么是扩展欧几里得算法？ (What is the Extended Euclidean Algorithm?)

相关文章：

eclipse 重启/打开内置浏览器

JConsole的使用

折线图表动画（历史进程效果）

不要只是为您的代码做些毛-用Prettier修复它

循环语句（2）

通过Shell脚本将VSS项目批量创建并且提交迁移至Gitlab

样式集（11）注册页面样式，全部代码附效果图

quickselect_QuickSelect：使用代码示例解释的快速选择算法

《Linux命令行与shell脚本编程大全第3版》Shell脚本编程基础---34

CSS超出部分隐藏，显示滚动条

第二周学习进度

如何在C ++中从容器中删除元素

【BZOJ4282】慎二的随机数列乱搞

git phpstorm 配置

CSS动画无限循环

apple id无法创建_我如何为我的Apple收藏夹创建网站

bzoj1562[NOI2009]变换序列——2016——3——12

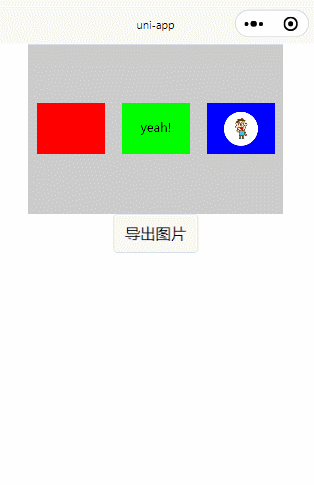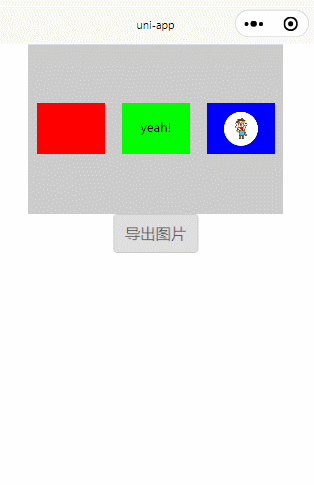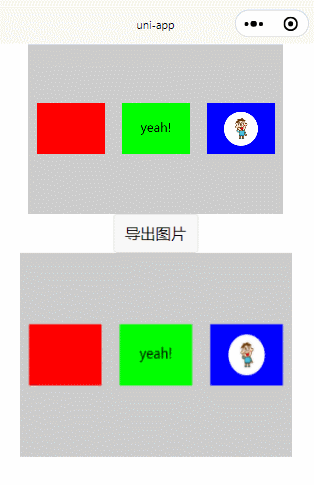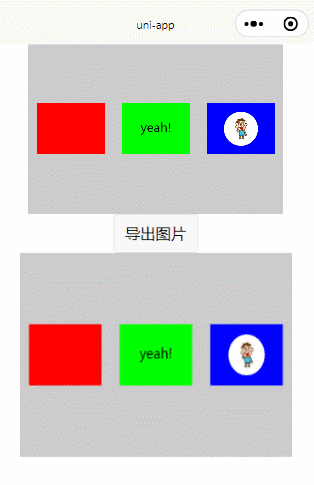
把view或者div绘制 canvas ，导出图片功能实现完整源码附效果图（兼容H5和小程序）

C 语言中的 switch 语句 case 后面是否需要加大括号

问题 c: 插入排序_插入排序：它是什么，以及它如何工作

在Java连接hbase时出现的问题

codeforces 8C. Looking for Order 状压dp

H5刷新当前页面

sql的外键约束和主键约束_SQL主键约束用示例解释

str.format() 格式化字符串函数

css学习任务二：切图写代码

Vue mixins（混入）附代码示例详解

软件开发面试_如何为成功的软件开发工作面试做准备

bzoj1070————2016——3——14

CSS兼容性汇总