leetcode dfs_深度优先搜索:具有6个Leetcode示例的DFS图遍历指南
leetcode dfs
Have you ever solved a real-life maze? The approach that most of us take while solving a maze is that we follow a path until we reach a dead end, and then backtrack and retrace our steps to find another possible path.
您是否解决了现实生活中的迷宫? 我们大多数人在解决迷宫时采取的方法是:沿着一条路直到到达死胡同,然后回溯并追溯我们的步骤以找到另一条可能的路。
This is exactly the analogy of Depth First Search (DFS). It's a popular graph traversal algorithm that starts at the root node, and travels as far as it can down a given branch, then backtracks until it finds another unexplored path to explore. This approach is continued until all the nodes of the graph have been visited.
这正是深度优先搜索(DFS)的类比。 这是一种流行的图形遍历算法,从根节点开始,一直沿给定分支向下传播,然后回溯直到找到另一条未探索的路径。 继续进行此方法,直到访问了图的所有节点为止。
In today’s tutorial, we are going to discover a DFS pattern that will be used to solve some of the important tree and graph questions for your next Tech Giant Interview! We will solve some Medium and Hard Leetcode problems using the same common technique.
在今天的教程中,我们将发现一种DFS模式,该模式将用于解决您下一次Tech Giant采访中的一些重要的树形图问题! 我们将使用相同的通用技术解决一些中度和硬性Leetcode问题。
So, let’s get started, shall we?
所以,让我们开始吧?
实作 (Implementation)
Since DFS has a recursive nature, it can be implemented using a stack.
由于DFS具有递归性质,因此可以使用堆栈来实现。
DFS Magic Spell:
DFS魔法:
- Push a node to the stack将节点推送到堆栈
- Pop the node弹出节点
- Retrieve unvisited neighbors of the removed node, push them to stack检索已删除节点的未访问邻居,将其压入堆栈
- Repeat steps 1, 2, and 3 as long as the stack is not empty只要堆栈不为空,重复步骤1、2和3
图遍历 (Graph Traversals)
In general, there are 3 basic DFS traversals for binary trees:
通常,对二进制树有3种基本的DFS遍历:
Pre Order: Root, Left, Right OR Root, Right, Left
预购:根,左,右或根,右,左
Post Order: Left, Right, Root OR Right, Left, Root
发布顺序:左,右,根或右,左,根
In order: Left, Root, Right OR Right, Root, Left
顺序:左,根,右或右,根,左
144.遍历二叉树(难度:中) (144. Binary Tree Preorder Traversal (Difficulty: Medium))
To solve this question all we need to do is simply recall our magic spell. Let's understand the simulation really well since this is the basic template we will be using to solve the rest of the problems.
要解决这个问题,我们要做的就是简单地回忆起我们的魔咒。 让我们很好地理解模拟,因为这是我们将用来解决其余问题的基本模板 。
At first, we push the root node into the stack. While the stack is not empty, we pop it, and push its right and left child into the stack.
首先,我们将根节点推入堆栈。 当堆栈不为空时,我们将其弹出,然后将其左右子项推入堆栈。
As we pop the root node, we immediately put it into our result list. Thus, the first element in the result list is the root (hence the name, Pre-order). The next element to be popped from the stack will be the top element of the stack right now: the left child of root node. The process is continued in a similar manner until the whole graph has been traversed and all the node values of the binary tree enter into the resulting list.
当我们弹出根节点时,我们立即将其放入结果列表。 因此,结果列表中的第一个元素是根(因此,其名称为Pre-order)。 从堆栈中弹出的下一个元素将是当前堆栈的顶部元素:根节点的左子节点。 以相似的方式继续该过程,直到遍历了整个图并且二叉树的所有节点值都进入结果列表为止。
145.二叉树后序遍历(难度:困难) (145. Binary Tree Postorder Traversal (Difficulty: Hard))
Pre-order traversal is root-left-right, and post-order is right-left-root. This means post order traversal is exactly the reverse of pre-order traversal.
顺序遍历是root-left-right ,而顺序遍历是right-left-root 。 这意味着后订单遍历与前订单遍历完全相反。
So one solution that might come to mind right now is simply reversing the resulting array of pre-order traversal. But think about it – that would cost O(n) time complexity to reverse it.
因此,现在可能想到的一种解决方案就是简单地逆转最终的遍历结果数组。 但是考虑一下–反转它会花费O(n)时间复杂度。
A smarter solution is to copy and paste the exact code of the pre-order traversal, but put the result at the top of the linked list (index 0) at each iteration. It takes constant time to add an element to the head of a linked list. Cool, right?
一个更聪明的解决方案是复制并粘贴预遍历的确切代码,但是在每次迭代时将结果放在链接列表的顶部(索引0)。 向链接列表的开头添加元素需要花费固定的时间。 酷吧?
94.二叉树有序遍历(难度:中) (94. Binary Tree Inorder Traversal (Difficulty: Medium))
Our approach to solve this problem is similar to the previous problems. But here, we will visit everything on the left side of a node, print the node, and then visit everything on the right side of the node.
我们解决此问题的方法与先前的问题类似。 但是在这里,我们将访问节点左侧的所有内容,打印该节点,然后访问该节点右侧的所有内容。
323.无向图中的连接组件数 (难度:中) (323. Number of Connected Components in an Undirected Graph
(Difficulty: Medium))
Our approach here is to create a variable called ans that stores the number of connected components.
我们这里的方法是创建一个名为ans的变量,该变量存储已连接组件的数量。
First, we will initialize all vertices as unvisited. We will start from a node, and while carrying out DFS on that node (of course, using our magic spell), it will mark all the nodes connected to it as visited. The value of ans will be incremented by 1.
首先,我们将所有顶点初始化为未访问。 我们将从一个节点开始,并且在该节点上执行DFS时(当然,使用我们的魔术咒语),它将把与其连接的所有节点标记为已访问。 ans的值将增加1。
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;public class NumberOfConnectedComponents {public static void main(String[] args){int[][] edge = {{0,1}, {1,2},{3,4}};int n = 5;System.out.println(connectedcount(n, edge));}public static int connectedcount(int n, int[][] edges) {boolean[] visited = new boolean[n];List[] adj = new List[n];for(int i=0; i<adj.length; i++){adj[i] = new ArrayList<Integer>();}// create the adjacency listfor(int[] e: edges){int from = e[0];int to = e[1];adj[from].add(to);adj[to].add(from);}Stack<Integer> stack = new Stack<>();int ans = 0; // ans = count of how many times DFS is carried out// this for loop through the entire graphfor(int i = 0; i < n; i++){// if a node is not visitedif(!visited[i]){ans++;//push it in the stackstack.push(i);while(!stack.empty()) {int current = stack.peek();stack.pop(); //pop the nodevisited[current] = true; // mark the node as visitedList<Integer> list1 = adj[current];// push the connected components of the current node into stackfor (int neighbours:list1) {if (!visited[neighbours]) {stack.push(neighbours);}}}}}return ans;}
}200.岛屿数量(难度:中) (200. Number of Islands (Difficulty: Medium))
This falls under a general category of problems where we have to find the number of connected components, but the details are a bit tweaked.
这属于一般问题类别,我们必须找到已连接组件的数量,但细节有所调整。
Instinctually, you might think that once we find a “1” we initiate a new component. We do a DFS from that cell in all 4 directions (up, down, right, left) and reach all 1’s connected to that cell. All these 1's connected to each other belong to the same group, and thus, our value of count is incremented by 1. We mark these cells of 1's as visited and move on to count other connected components.
本能地,您可能会认为,一旦找到“ 1”,便会启动一个新组件。 我们在该单元的所有4个方向(上,下,右,左)上执行DFS,并达到与该单元相连的所有1。 所有这些相互连接的1属于同一组,因此,我们的count值加1。我们将1的这些单元格标记为已访问,然后继续对其他连接的组件进行计数。
547.朋友圈(难度:中) (547. Friend Circles (Difficulty: Medium))
This also follows the same concept as finding the number of connected components. In this question, we have an NxN matrix but only N friends in total. Edges are directly given via the cells so we have to traverse a row to get the neighbors for a specific "friend".
这也遵循与查找已连接组件数相同的概念。 在这个问题中,我们有一个NxN矩阵,但总共只有N个朋友。 边缘是直接通过单元格给出的,因此我们必须遍历一行以获取特定“朋友”的邻居。
Notice that here, we use the same stack pattern as our previous problems.
请注意,在这里,我们使用与先前问题相同的堆栈模式。
That's all for today! I hope this has helped you understand DFS better and that you have enjoyed the tutorial. Please recommend this post if you think it may be useful for someone else!
今天就这些! 我希望这可以帮助您更好地了解DFS,并希望您喜欢本教程。 如果您认为此帖子可能对其他人有用,请推荐此帖子!
翻译自: https://www.freecodecamp.org/news/dfs-for-your-next-tech-giant-interview/
leetcode dfs
相关文章:

MySQL排序原理与MySQL5.6案例分析【转】
本文来自:http://www.cnblogs.com/cchust/p/5304594.html,其中对于自己觉得是重点的加了标记,方便自己查阅。更多详细的说明可以看沃趣科技的文章说明。 前言 排序是数据库中的一个基本功能,MySQL也不例外。用户通过Order by…
7.RabbitMQ RFC同步调用
RabbitMQ RFC同步调用是使用了两个异步调用完成的,生产者调用消费者的同时,自己也作为消费者等待某一队列的返回消息,消费者接受到生产者的消息同时,也作为消息发送者发送一消息给生产者。参考下图: 调用流程如下&…
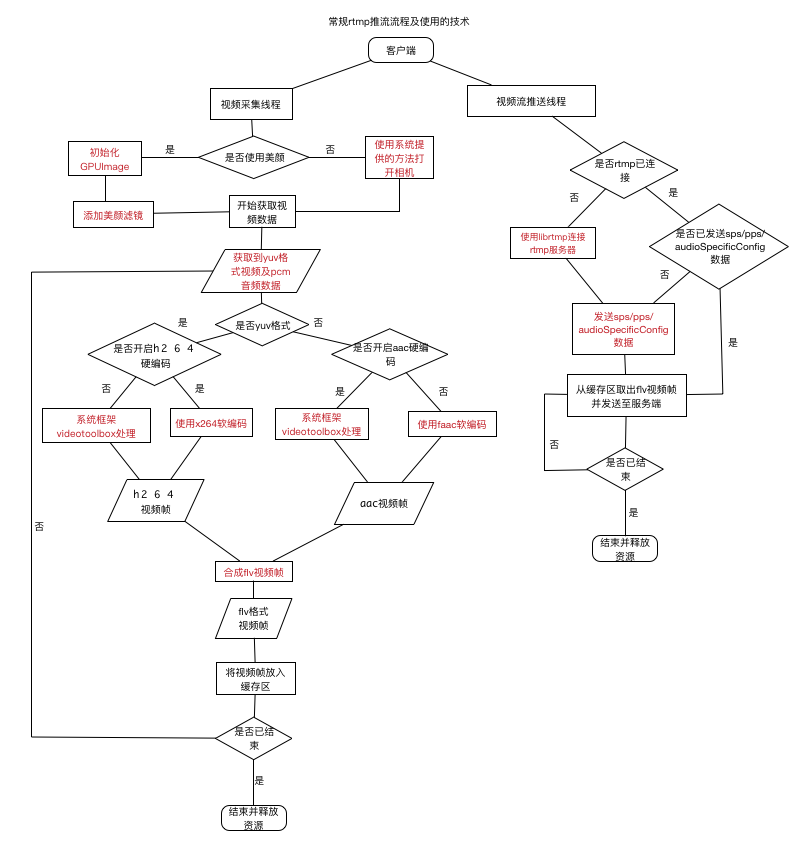
1小时学会:最简单的iOS直播推流(二)代码架构概述
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…
sh脚本每天创建一个文件夹_我每天创建一个月的视频。 这就是发生的事
sh脚本每天创建一个文件夹At the end of 2019 I promised that 2020 would be all about my YouTube channel. So thats what Ive been doing. 😃 在2019年底,我保证2020年将成为我的YouTube频道的全部 。 这就是我一直在做的。 😃 On the f…

1小时学会:最简单的iOS直播推流(三)使用系统接口捕获音视频数据
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

什么是bower
Bower是一个客户端技术的软件包管理器,它可用于搜索、安装和卸载如JavaScript、HTML、CSS之类的网络资源。其他一些建立在Bower基础之上的开发工具,如YeoMan和Grunt,这个会在以后的文章中介绍。 准备工作 安装node环境:node.js安装Git&#x…

ES6中export及export default的区别
在ES6中,export和export default均可用于导出常量、函数、文件、模块等,你可以在其他文件或模块中通过import (常量 | 函数 | 文件 | 模块)名的方式将其导入,以便能够对其进行使用,但在一个文件或模块中,export、impo…

sm2加密算法实例_实例说明加密算法
sm2加密算法实例Cryptography, at its most basic, is the science of using codes and ciphers to protect messages. 密码学从根本上讲就是使用代码和密码保护消息的科学。 Encryption is encoding messages with the intent of only allowing the intended recipient to un…

git---远程仓库版本回滚
开发中,发现有错误版本提交带远程分支master,怎么处理? 1 简介 最近在使用git时遇到了远程分支需要版本回滚的情况,于是做了一下研究,写下这篇博客。 2 问题 如果提交了一个错误的版本,怎么回退版本&#x…

1小时学会:最简单的iOS直播推流(四)如何使用GPUImage,如何美颜
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

团队任务四(无图)
任务要求: WBS练习对团队项目进行任务分解要求所有人共同参与队长列出需求成员进行估计队长领导大家达成共识形成团队报告,发至团队博客项目分解: 一、手机监控(24h) (1)手机当前运行程序监控(用以观察用户…

react测试组件_测试驱动的开发,功能和React组件
react测试组件This article is part of my studies on how to build sustainable and consistent software. In this post, we will talk about the thinking behind the testing driven development and how to apply this knowledge to simple functions, web accessibility,…

CDOJ 1073 线段树 单点更新+区间查询 水题
H - 秋实大哥与线段树Time Limit:1000MS Memory Limit:65535KB 64bit IO Format:%lld & %llu Submit Status Practice UESTC 1073Appoint description: System Crawler (2016-04-24)Description “学习本无底,前进莫徬徨。” 秋实大哥对一旁玩手机的学…

1小时学会:最简单的iOS直播推流(五)yuv、pcm数据的介绍和获取
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…
beta冲刺第一天
1、今天解决的进度 成员进度陈家权回复界面设计,由于成员变动加上和其他成员距离较远,服务器404赖晓连改进Alpha版本页面没能及时更新的问题雷晶获取提问问题时间更新到数据库林巧娜今天的任务是夜间模式功能块,没有完成,查找了很…

angular绑定数据_Angular中的数据绑定说明
angular绑定数据数据绑定 (Data Binding) 动机 (Motivation) Data often defines the look of an application. Interpreting that data into the user interface involves class logic (.component.html) and a template view (.component.ts) . Angular connects them throug…

WPF判断两个时间大小避免误差
进行查询操作的时候,经常用到判断开始时间和结束时间大小的条件,由于从控件上获取的时间除了年月日时分秒,还包括毫秒、微秒等,导致直接判断时间大小的时候会产生一些误差,如下: 结果分析:年月日…

1小时学会:最简单的iOS直播推流(六)h264、aac、flv介绍
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

分享一款Markdown的css样式
使用 本样式在这个样式的基础上做了一些修改, 主要是对于表格和代码块以及一些细节的修改。 主要目的是用在chrome的扩展 Markdown Preview Plus中, 替换其内置的样式。 由于 Markdown Preview Plus对css文件大大小有要求(小于8K)…

远程桌面怎么持续连接_如何拥有成功且可持续的远程产品管理职业
远程桌面怎么持续连接Remote work is rapidly growing in all industries. Some professionals might try to push away this new way of working, seeing it as simply a current necessity. They might not think its fit for a product manager who’s constantly managing …

1小时学会:最简单的iOS直播推流(七)h264/aac 硬编码
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

Linux日常命令记录
1、查找进程 ps -ef | grep javajps 2、杀死进程 kill -9 1827 3、进入tomcat中的日志文件夹 cd logs 4、查看日志 tail -f catalina.outtail -n 10000 catalina.out 5、查看tomcat的连接数 ss -nat|grep -i "8081"|wc -lnetstat -nat | grep -i "8081" | …

【特效】移入显示移出隐藏
移入显示移出隐藏的效果也是很常见的,例如: 如果页面有有多处地方有此效果,那么也可以合并到一块,只写一段js代码,只要注意控制样式和class名字和用于js获取元素的class名字分开设置就可以了。代码很简单,用…

web前端开发最佳实践_学习前端Web开发的最佳方法
web前端开发最佳实践为什么要进行网站开发? (Why web development?) Web development is a field that is not going anywhere anytime soon. The web is moving quickly, and there are regular improvements to the devices many people use daily. Web开发是一个…

使用C#的HttpWebRequest模拟登陆网站
很久没有写新的东西了,今天在工作中遇到的一个问题,感觉很有用,有种想记下来的冲动。 这篇文章是有关模拟登录网站方面的。 实现步骤; 启用一个web会话发送模拟数据请求(POST或者GET)获取会话的CooKie 并根…

1小时学会:最简单的iOS直播推流(番外)运行不起AWLive的demo的同学请看这里
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

学习css布局
非常经典 http://zh.learnlayout.com/ float和position:absolute都是inline-block,破坏性的。absolute根据父元素定位(static父元素除外)。div也将不再是一行的块了。 position:relative自身定位。top,left是根据自己原本位置&…
csv文件示例_如何在R中使用数据框和CSV文件-带有示例的详细介绍
csv文件示例Welcome! If you want to start diving into data science and statistics, then data frames, CSV files, and R will be essential tools for you. Lets see how you can use their amazing capabilities.欢迎! 如果您想开始研究数据科学和统计学&…

1小时学会:最简单的iOS直播推流(八)h264/aac 软编码
最简单的iOS 推流代码,视频捕获,软编码(faac,x264),硬编码(aac,h264),美颜,flv编码,rtmp协议,陆续更新代码解析,你想学的知识这里都有…

003小插曲之变量和字符串
变量:赋值(名字值);变量名:字母分大小写/数字/下划线,不能以数字开头;拼接;原始字符串r; 专业优秀的名称:teacher/num/name/test/temp >>> teacher小…
