当前位置：首页 > 编程日记 > 正文

pta函数统计素数并求和_黎曼的zeta函数

编程日记 2024-06-18 10:40:00

9月24日阿提亚爵士（Sir Atiyah）直播“证明”黎曼猜想（Riemann hypothesis）在普通人中引发了一轮数学热潮，网络上一时间涌现了很多数学八卦文章。许多人在论及该命题重要性时都指出，ζ函数的非平凡零点与素数分布有关，却未更进一步说明怎么个有关法。这个“有关”如果没有一定数学基础，把答案摆在面前也不一定能看明白。我对相关话题有一点浅显的认识，所以想谈一些比八卦文章更深入的东西，但也不想入得太深，非数学专业理工科学生能跟上就好。

我想尽量简洁地科普黎曼函数几条皮毛的皮毛的皮毛的知识，包括：

ζ是定义在几乎全部复平面上的解析函数；
负偶数是ζ的零点；
ζ的非平凡零点位于一个带状区域；
ζ的非平凡零点与素数计数有关。

本文假设读者通晓微积分，知道复数。由于这不是数学教材或论文，很多计算过程会被跳过，定理的证明会被省略。

那么我们开始吧。

复分析提要

因为不确定是否所有学微积分的专业都要学复变函数，所以还是先提一下。

本文提到的函数除非另有说明，均为解析函数。对于复变量

为其实、虚部。一个复数域上的函数可以看成定义在

上的实变量函数。当我们说一个复函数

是解析的，除了要求它对变量

可微，更进一步还要求其满足柯西-黎曼方程（Cauchy-Riemann equations）

C-R方程是一个极强的限制，一些很简单的函数例如Re(z), Im(z), |z| 因此都被排除出了解析函数的范围。它使得复解析函数具有许多漂亮的性质，譬如：

若函数
在开区域
内解析，在其闭包
连续，那么
在
内无限可微，在
内任意点
附近总有幂级数展开，且收敛半径大于0. 在点
处的各阶导数值为(
为区域边界)

如果函数
在
内没有极点，那么
整函数（在整个复平面解析的函数）
如果不是常函数，其值域与复数域至多相差一个元素。例如多项式函数遍历复数域，指数函数遍历
.更进一步，如果整函数
还不是多项式，则除去一个可能存在的例外，对于值域中的每一点A，方程
都有无穷多个解；A为例外点时方程无解或只有有限个解。

我们说点

是函数

的一个

级极点或零点，简单说是指当自变量

靠近

时，函数表现得像是

或

，

为非零复常数。

再介绍一个在复分析中极为重要的概念，解析延拓。假设解析函数

分别定义在开区域

上，若

非空且两个函数在

取值相等，那么存在定义在

上的解析函数

,它在

上和

相等，

这看上去平平无奇，即便在实函数情形下也很显然。区别在于，实函数的解析延拓有无穷多种方式，而复函数的延拓方式是唯一的（证略）

举个例子，

作为实函数如果要延拓到全平面且在所有点都任意可微，可以是常函数也可以是以下函数族中的任意一个（当然还有其它很多种选择）

然而如果将

视为复函数，它的解析延拓只能是常函数。

现在考虑如下两个函数

和

在其公共定义域

上是相同的，我们说

是

的一个解析延拓，在这层意义上，有时会有人说

和

是相同的函数。当需要计算发散的几何级数时，比如计算

,会用

来代替（小孩子不要学）。这看似荒谬的结果其实还能牵扯到无穷级数求和怎么定义的问题，只能是柯西和吗？这里就不进一步展开了，有兴趣的读者可以参考这里

全体自然数的发散级数和等于负十二分之一代表了什么？隐藏了一个天大的秘密吗？www.zhihu.com

还是

的最大解析延拓。因为无法找到一个解析函数，它的定义域真包含

（如果存在，这样的定义域只能是

,但这个函数在

处不连续）

当我们研究一个复解析函数时，如果它的定义域未铺满全平面，一个很自然的想法是寻找它的最大解析延拓。

用无穷级数定义黎曼的Zeta函数

定义：

. 我们在微积分课堂上就知道这个无穷级数只在

收敛（当然，如果你是某方士或其信徒，我觉得本文你不用看下去了），如果它是复变量函数呢？

复分析中有条结论说如果

收敛，则

也收敛。由此可知

的无穷级数定义可以直接推广到

区域。

现在看它的零点，当自变量为实数时显然

,自变量为复数时，利用算数基本定理和乘法分配律，我们将函数重写为

取遍所有素数，这里我们第一次把

和素数联系起来。

由于每一点的模长都大于0，因此该函数没有零点。

Zeta的最大可延拓区域

看到上一节的结论，有的读者可能就要拍桌子了

那么多大数学家在找它的零点，你居然说不存在，这不扯吗。我就是没看明白你的过程也敢说肯定有哪里错了，毕竟大神们不可能集体犯错吧？

大神们当然没错，我也没错，因为上一节只得到函数在

时没有零点。在这之外的区域，我们要先把函数延拓出去才能讨论。很多文章里都提到过

是定义在

上的函数，但这从原始定义很难看出。为此，我们考察下面这个函数

为

的幅角，在

取值。

看到这个积分限，也许又有人不满了

积分上下限相同，这摆明了是0嘛！

当然没那么简单，实际的积分路径由三部分组成：

1.从正无穷沿着正实轴到一个很小的正数

，幅角为0

2.以原点为圆心，逆时针旋转一圈

3.从

沿着正实轴到无穷远处，幅角为

最后还要取极限

被积函数在

有1级极点(x=0不一定是1级极点，但不影响结论)，而积分路径可以避开所有极点。

的时候，函数被指数压低，无论

如何取值都会收敛。也就是说，

是整函数。

这个积分在

时很容易算出

,其中

是已经被人们研究得很透彻的欧拉（Euler）伽马函数。伽马函数没有零点，除了0和负整数为其1级极点，它在全平面解析。为了之后书写简便，我们作一个平移，用

替代它。对于自然数

利用两条性质：

,我们有

.等号两边都是解析函数，尽管该方程是在

得到的，但可由解析延拓的理论得到它在两边的最大延拓区域上也成立。由于

无极点，

只在

有1级极点，所以

是

上的解析函数。然而之前已经得到了

在

收敛，

在定义域内。至于

,沿着实轴从右侧取极限可知函数该点发散，无法通过取特定值消除不连续性，所以

的最大延拓区域为

现在考察自变量趋近于1时的渐进行为，以确定这是它的几级极点。在

时有

,发散出现在积分变量t接近0的部分，此时被积函数近似

,所以

,1是函数的1级极点。

Zeta的平凡零点

先介绍伯努利数（Bernoulli numbers），将以下函数作泰勒展开（Talor expansion）

展开系数被称为伯努利数（不同文献中对伯努利数的定义略有区别），它们都是有理数。由于

是偶函数，所以除了

，其他的奇伯努利数都为0.

令

,我们有

一些脍炙人口的结论，例如

便可由此得到。如同之前举例的函数

和

,在需要计算全体自然数之和的场合，人们总说它为-1/12

之前说了，奇伯努利数几乎全为0，所以当

为负偶数时，

.这个性质太过简单，这些零点被人们称作zeta函数的平凡零点。

顺便一提，欧拉在研究zeta函数时，对于正偶数情形得到了

这个结果实在是令人讶异，也是让我被zeta函数吸引的最初原因。一个只与自然数幂有关的级数里怎么会冷不丁地冒出圆周率来？我不打算在此证明这个一般性的结论，对于

，下面这个用物理思想进行计算的视频，是我见过最有趣的方法了。

https://www.bilibili.com/video/av20400157/www.bilibili.com

我尤其喜欢这句话“如果你看到

,在错综复杂的庞大数学网络中，就会有一条路把你带回几何学中的圆”，条条大路通罗马的感觉有没有？

非平凡零点关于1/2对称

下文开头抛了一个“众所周知”的方程，我本来还想证一下，但既然大家都知道，那就直接拿来用好了。

罗旻杰：积分变换和 Riemann zeta 函数的函数方程zhuanlan.zhihu.com

用

替换众所周知方程中的

，我们得到

利用前述

函数的两条性质，并进一步注意到（其实我感觉一般人注意不到）

,我们有如下长得很对称的方程

定义新的函数

,由上面的方程可知对称性

处于1级极点，

会将其抵消；

为负偶数时

处于1级极点但

的平凡零点会将其抵消。这说明

是整函数，它不是常函数，几乎肯定有无穷多零点。黎曼断言，对于充分大的正数T,虚部位于[0,T]区间内的零点数量约为

，相对误差在

量级。黎曼觉得这个结论很简单大家都能得到，也就没写计算过程。他实在是太高估同行们了，这个结论直到1905年才由曼戈尔特（von Mangoldt）给出证明，此时距离黎曼去世已经快40年了。

由于

没有零点，因此

在自变量实部大于1时无零点，再由对称性，实部小于0时也没有零点（从这里可以看出zeta的所有平凡零点都是1级零点），所以zeta的非平凡零点全部位于带边条状区域

1896年阿达玛（Hadamard）和普桑（Poussin）各自独立证明边界上没有零点，去掉边界之后的区域现在被人们称作临界带。

zeta函数与素数计数的关系

说了这么多，黎曼研究这个函数他到底是想干嘛？黎曼的研究写在了他的8页论文《On the Number of Primes Less Than a Given Magnitude》，他的目的是了解素数的分布规律，具体说是要得到素数计数函数。

现在起要加快车速，只摆结果了，因为涉及到的每一个方程，证明过程都只是单纯往死了算。

引入莫比乌斯函数（Möbius function），定义域为

这样有

引入阶跃函数J(x)，定义域为[0,+∞]

J(0)=0;若x不是某个素数的幂，那么在x的足够小邻域内J为常数；若x为某个素数的n次幂，则在此处有幅度为1/n的跳变，即对任意的0<a<1, J(x+a)-J(x-a)=1/n, J(x)-J(x-a)=1/2n.

把前几段显式表达出来为

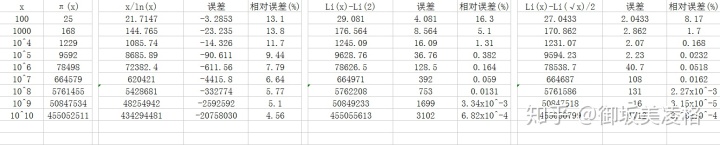
看得出来这东西并不好算，假如我们想知道J(100)的值，要把100以内的所有素数和它们的幂都找出来，然后累加。打开素数表，可以数出来幅度为1的跳变数（即100以内的素数个数）为25；幅度为1/2的跳变次数为4（4、9、25、49）；幅度为1/3、1/4的跳变次数为2（8、27、16、81）；幅度为1/5、1/6的跳变次数为1（32、64）。

，再往上不用算了。于是可以得到J(100)=25+4/2+2/3+2/4+1/5+1/6=28.5333……当自变量很大时，这项工作就很困难了。

素数计数函数，这个函数用的字母和圆周率相同，是历史遗留的习惯

={ (0,x)内素数的个数+(0,x]内素数的个数 }/2, 易知

黎曼放话说

,这看上去是无穷求和，但从

开始每一项都为0, 所以对任意x都是有限求和，不需要考虑敛散性。

快完了，到最后一个定义了

这东西怎么延拓我也不管了，总之黎曼经过一通骚操作之后得到了他在著名的8页文里的结论

他要的其实就是这个公式。这一坨东西里头第一项最重要，积分要比挨个找素数幂容易多了，后面的都是误差修正项。右边末项就是个常数ln(1/2)；第三项衰减得比

还快，

越大第三项越可忽略；第二项求和，ρ遍历ξ所有虚部大于0的零点，这个误差一眼看不出来，暂时也没人算出来，但通过之后的表格可以稍微感受下它

在x不是特别大的时候没多大影响。这便是zeta函数零点和素数计数的关系。

黎曼写那篇文章的目的是为了得到计数函数的估计值，在他之前

即

都曾被用作

的近似函数。但黎叔说他的函数比这些都准（那是当然，你这是精确表达式），重要的是把那一坨误差项丢掉，结果也比它们准，收敛得也极快。我们只取前2项，拿

来对比

看起来J(x)的第二项确实影响不大

结尾

有个很重要的问题还没说，零点实部是否全是1/2（即黎曼猜想）我提都没提，黎叔的猜想究竟和哪些重要的命题有怎样的联系也没讲。原因很简单，我也不知道233333但是一点不说也不好，所以我就从维基百科搬运一点。

如果用
估计
，从上节的表中看到仿佛总有
，这在
是肯定成立的。虽然人们还没找到令不等号反向的例子，但可以证明对任意正数M，总存在x、y>M使得

由此可知，函数

会变号无穷多次。

误差
, 其中
是零点实部的上确界,显然
.
是很糟糕的情况，毕竟
，误差变得比天然的上界还要大。然而目前为止，人们对
的估计仍停留在这个闭区间。
如果假设黎曼猜想成立，那么可以得到当x>2657时，
，相对误差随着x增大会趋于0.

数学专业的哪里用得着看本文学知识，非数学专业的如果一路看下来还很兴奋，那接着看文献好了，毕竟推导更严格内容更深。如果你能把本文跟下来而且没天才到一眼看穿所有算式，我想你对这些数学问题的难度有多大又会有新的认识。原来读科普、数学史甚至营销号蹭热点的八卦文可能是站在海平面看珠峰，就看见老远有个坡；现在可能往高处走了几步，还没能看到半山腰。至于云层之上有多高多难爬，其实仍然没有感觉。

我是学物理的，这东西只是本科在学统计力学时闲得蛋疼看着玩的。本来好多年没管了，但阿提亚前几天又搞了个大新闻，各路科普我又感觉太浅，那趁此机会把我知道的总结下吧。这么naive的内容，本来想发企鹅空间，但辣鸡企鹅敲不了公式，于是只能（冒着随时被数学大佬公开处刑的风险）放到公开场合。解析数论对我来说太过艰深，兴趣不大，实际上我对几何更感兴趣。陈省身有言：复流形的美怎么描述都不为过。我觉得，如果能理解这句话，体会到他的感受，此生无憾。

ps:等真吃到碗里的鬼知道我会不会又瞄着锅里，TMD，这无涯的学海真操蛋！

https://www.dkcj.cn/info/11239.html

pta函数统计素数并求和_黎曼的zeta函数

相关文章：

EasyRTMP手机直播推送rtmp流flash无法正常播放问题

对称加密和非对称加密

防火墙iptables介绍

企业局域网的组建

python3 线程池源码解析_5分钟看懂系列：Python 线程池原理及实现

区块链+能源，能擦出什么样的火花？

JS学习梳理（三）类型和语法

北师大历史系65 级同学聚会宁夏【之七】——在中阿之轴、西夏王陵、董府、板桥道堂、鸿乐府及告别宴会...

会声会影水墨遮罩如何变大_自媒体长期网赚项目：自媒体如何打造自己的自媒体知识付费课程（干货）...

OBS源代码阅读笔记

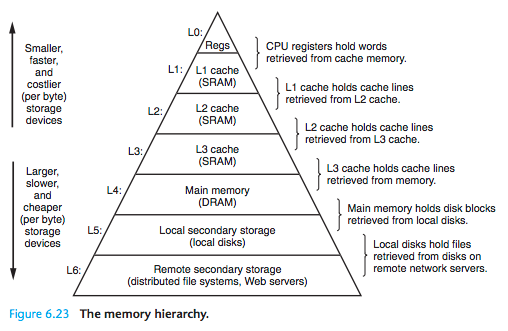
存储器结构层次（二）

python 核心编程第十三章

python写一个文件下载器_Python3使用TCP编写一个简易的文件下载器

提取Jar2Exe源代码，JavaAgent监控法

并发编程之多进程

x9此计算机上没有hasp_mastercam x9安装步骤

bitcoinj开发环境搭建

static关键字用法

swift x输入流_SwiftUI 探索 - 状态和数据流

qt 控件背景色透明除去边框

A Strange Bitcoin Transaction

Jsoncpp 使用方法解析

tomcat限速_WEB服务的下载限速（二)(限速模块安装与配置)

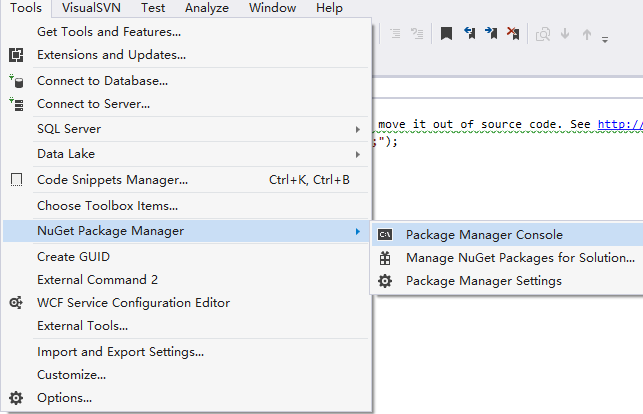
EntityFrameworkCore 安装

python神秘的魔法函数_Python魔法函数

HDU-4738-Caocao's Bridges（tarjan）

博客园美化技巧汇总

数据事务四种隔离机制和七种传播行为

vue注册新节点_vue怎么重新组装slots节点

什么是EOS？