poj_2762,弱连通

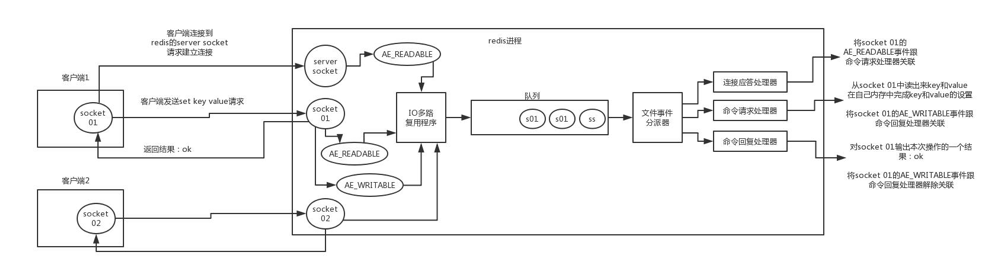
http://poj.org/problem?id=2762

这题是求弱连通

弱连通就是无向图强连通（基图是有向图）

思路：先targan缩点，然后这些点求最长链

也就是这些点（缩点）在一棵树上，这棵树的深度应该为强连通分量个数。。

画个图就好理解了

#include<cstdio>
#include<cstring>const int maxn(1111);
struct Edge{int v, next;
}e1[maxn*6], e2[maxn*6];
int head1[maxn], cnt1, head2[maxn], cnt2;
int low[maxn], dfn[maxn], vis[maxn], belong[maxn];
int stack[maxn], step, color, top;
void init(){memset(head1, -1, sizeof head1);cnt1 = cnt2 = 0;memset(head2, -1, sizeof head2);memset(vis, 0, sizeof vis);memset(dfn, 0, sizeof dfn);memset(belong, -1, sizeof belong);step = color = top = 0;
}
void add_Edge(int u, int v){e1[cnt1].v = v, e1[cnt1].next = head1[u];head1[u] = cnt1 ++;
}
int n, m;
int f[maxn][maxn], ind[maxn];void targan(int u){dfn[u] = low[u] = ++ step;stack[top++] = u;vis[u] = 1;for(int i = head1[u]; i != -1; i = e1[i].next){int v = e1[i].v;if(!dfn[v]){targan(v);if(low[u] > low[v])low[u] = low[v];}elseif(vis[v] && low[u] > dfn[v])low[u] = dfn[v];}if(dfn[u] == low[u]){color ++;int s;do{s = stack[--top];vis[s] = 0;belong[s] = color;}while(s != u);}
}
void add_edge(int u, int v){e2[cnt2].v = v, e2[cnt2].next = head2[u];head2[u] = cnt2 ++;
}
int dp[maxn];
int cnt;
void dfs(int u){for(int i = head2[u]; i + 1; i = e2[i].next){int v = e2[i].v;if(dp[v] < dp[u] + 1)dp[v] = dp[u] + 1;if(dp[v] > cnt) cnt = dp[v];dfs(v);}
}
int check(){cnt = 0;int u;for(int i = 1; i <= color; i ++){if(ind[i] == 0){cnt ++;if(cnt > 1) return 0;u = i;}}/*cnt = 1;printf("%d\n", e2[u].next);while(e2[u].next != -1){cnt ++;u = e2[u].v;puts("|asdf");}*/memset(dp, 0, sizeof dp);cnt = 0;dfs(u);if(cnt == color - 1) return 1;return 0;
}
void solve(){for(int i = 1; i <= n; i ++)if(!dfn[i])targan(i);if(color == 1){puts("Yes");return;}memset(ind, 0, sizeof ind);memset(f, 0, sizeof f);for(int i = 1; i <= n; i ++){for(int j = head1[i]; j + 1; j = e1[j].next){int v = e1[j].v;int u = belong[i];v = belong[v];if(u != v && !f[u][v]){add_edge(u, v);ind[v] ++;f[u][v] = 1;}}}if(check())puts("Yes");elseputs("No");
}
int main(){int tcase;scanf("%d", &tcase);while(tcase --){init();scanf("%d%d", &n, &m);while(m --){int u, v;scanf("%d%d", &u, &v);add_Edge(u, v);}solve();}return 0;
}
/*
1
7 8
1 2
3 1
3 2
2 4
4 7
4 5
5 6
6 4
YES
*/