当一个序列满足对于任意的前 项和都满足不小于_时间序列分析第01讲--平稳序列(基本概念,线性平稳序列)...
第一章 平稳序列
1.1平稳序列基本概念
无论是从原序列中把趋势项去掉得到的随机波动项,还是用随机差分后得到残差序列,都会存在一种现象:随机项会沿着水平值波动,并且前后之间具有相关性,与独立序列不同。
一、定义
定义1.1 如果时间序列
- 对任何
----等于没说,也就是随机变量性质稍微好点
- 对任何
----这个也不本质,取0也可以
- 对任何关键!
---
那么我们称
例1.1 平稳序列的线性变换依然是平稳序列
那么
可见
如果取
例1.2 调和平稳序列
设
是平稳序列.
证明:验证期望为常数,协方差只与时间间隔有关
说明:计算期望时用到三角函数在一个周期内的积分为0。计算协方差时,用到积化和差公式得到一个常数加一个三角函数,然后用三角函数在一个周期内积分为0。
二、自协方差函数性质
自协方差函数有以下三条性质:
- 对称性:
- 非负定性:
对任意
- 有界性:
对称性证明:用到了协方差的对称性
非负定性证明:
任取一个向量
对于第一个等号,可以看做是一个求和,其中求和的每一项就是分别从三部分中取一个然后相乘,即
有界性证明:运用Schwarz不等式
反过来,只要实数列满足这三个条件,就可以构造随机序列,使得该序列的协方差函数为该给定的实数列!
三、非负定性、随机变量的线性相关
首先根据非负定性的证明有
进而如果
此时称
更进一步,如果
四、自相关系数
定义1.2 设平稳序列
我们把这样标准化后序列的自协方差函数成为
五、白噪声、白噪声模拟
定义1.3 设平稳序列
则称
- 如果序列是独立的,称为独立白噪声
- 如果序列均值为0,称为零均值白噪声
- 如果序列均值为0方差为1,称为标准白噪声
- 如果正态白噪声.
服从正态分布,称为
六、正交和不相关性
如果
对于两个平稳序列
- 不相关:
- 正交:
之所以这样定义正交,是从几何角度来看。事实上对于所有二阶矩存在的随机变量,构成一个Hilbert空间,且Hilbert空间上内积就用数学期望来定义.
两个平稳序列之和是否还是平稳序列?下面这个定理给出了说明:
定理1.1 对于平稳序列
证明:
二阶矩有界:
均值常数:
当正交的时候:
当不相关的时候:
1.2线性平稳序列和线性滤波
几种常用且重要的平稳序列
- 有限运动平均
- 线性平稳序列
- 时间序列的线性滤波
一、有限运动平均
设
是白噪声
- MA的平稳性
验证一下数学期望和自协方差函数的条件:
数学期望:
自协方差函数:
其中第3个等号利用白噪声的不相关性,只有
二、线性平稳序列
将有限运动平均改为无穷项会发生什么?定义零均值白噪声的无穷滑动平均为
当满足
当求和项数无限时,不能够轻易将期望与求和交换,那么如何证明平稳?
定理2.1 (单调收敛定理)如果非负随机变量序列单调不减
利用这个定理,我们令
因此利用单调收敛定理得到
但是无穷滑动平均的定义中没有绝对值,怎么办?
定理2.2 (控制收敛定理)如果随机变量序列
首先考察期望。由上面的讨论,我们得到在绝对值情形下的数学期望为
我们取
然后还要考察
至于为什么能交换,也就是单调收敛定理与控制收敛定理的应用,具体来说就是先考察各项都取绝对值后的期望是否存在,在这里就是
其期望可计算如下:
其中第一个等号运用单调收敛定理,即对于正项级数的期望和求和可交换,不等号运用了Schwarz不等式,最后一个小于号利用了绝对可和性。
最后说明一下二阶矩有界。这里也是Schwarz不等式的运用,如下:
注1:绝对可和条件下,如上定义的自协方差函数是绝对收敛的。
证明:
这说明了自协方差函数当
单边线性序列:只对非负部分求和,即
相关文章:

京医通如何删除临时卡,解绑
1、解绑的话,如果你是正式卡或者社保卡,可以在账户里面,点击卡进去详情页,里面会有一个解绑 2、重点就是临时卡了,挂号的时候很恶心。 目前唯一的解决办法就是,注销账户。 1)、解绑所有正式卡 2…
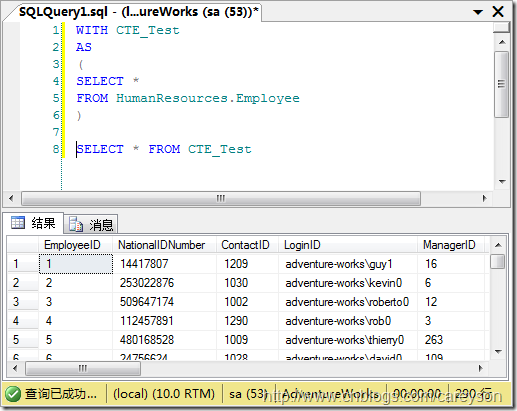
T-SQL查询——详解公用表达式(CTE)
对于Select查询语句来说,通常情况下,为了是T-SQL代码更加简洁和刻度,在一个查询中应用另外的结果集都是通过视图而不是查询进行分解的,但是,视图作为系统对象存储在数据库中,那对于结果集仅仅需要在存储过程…

如何实现显示超过10个字符就显示省略号?
// 要展示的文本(nickName) this.nickName 风一样的女子凤一样的我,有想认识嘛~~ if (this.nickName.length > 10) {this.nickName this.nickName.substring(0, 10) "...";console.log(00, this.nickName)}备注:substring() 方法用于提取…

课程实验代码及动手动脑测试
枚举类型测试代码: public class EnumTest {public static void main(String[] args) {Size s Size.SMALL;Size t Size.LARGE;// s和t引用同一个对象?System.out.println(s t); //// 是原始数据类型吗?System.out.println(s.getClass().is…

python利用自动识别写模块_Python 利用pytesser模块识别图像文字
使用的是python的pytesser模块,原先想做的是图片中文识别,搞了一段时间了,在中文的识别上还是有很多问题,这里做记录分享。 可将图片中的文字转换成文本(主要是英文)。 1.pytesser安装 使用设备:…

C02-程序设计基础提高班(C++)第9周上机任务-类和对象
第9周:阅读教材第8章(p231-262),主要内容是类和对象,学会定义类和对象解决问题,完成第9周上机任务;(回到C02-程序设计基础提高班(C)学习安排)实践任务:【任务…

在不影响配置下,清除netscreen密码
在缺省情况下,设备恢复特征被启用。可通过输入 unset admin device-reset 命令禁用它。同样,如果NetScreen 设备处于 FIPS 模式,恢复特征被自动禁用。1. 在登录提示下,键入设备的序列号。2. 在密码提示下,再次键入序列…

如何删除一个CSDN上自己上传的资源
如何删除一个CSDN上自己上传的资源 第一步,找到你想删除的资源,其URL举例为:http://download.csdn.net/detail/ssergsw/9733040则删除的get请求为:http://download.csdn.net/index.php/user_console/del_my_source/9733040删除成功…

关于计算机中二进制原码,反码,补码的简要解释
原码,补码,反码的概念 正数原码:正数的原码为取绝对值的数转二进制,5的原码为 00000000 00000000 00000000 00000101 负数原码:负数的原码为取绝对值的数转二进制,然后符号位(最高位&a…
python是一种面向对象的高级语言_爬了世纪佳缘后发现了一个秘密,世纪佳缘找对象靠谱吗?...
今天在知乎上看到一个关于【世纪佳缘找对象靠谱吗?】的讨论,其中关注的人有 1903,被浏览了 1940753 次,355 个回答中大多数都是不靠谱。用 Python 爬取世纪佳缘的数据是否能证明它的不靠谱?数据抓取 在 PC 端打开世纪佳…

使用邮件规则,将收到的邮件进行分类
随着工作的进行,我们经常会发现邮箱里一大堆各种各样的邮件,而要从中找到指定类型的邮件,只能每次都进行一次搜索。但是,经常这样搜索,先不说效率如何,它肯定会对我们的工作进行一些影响。 在这里ÿ…

多个CALayer的联动
在如何通过手势捕获CALayer基础上做了个示例,两个CALayer的联动,当拖动左侧的Layer的时候,右侧的Layer随动。因为右侧的动画没有关闭,有延迟,产生随动的效果。如果不想延迟,可参考拖动动画的问题及解决。 在…

在不允许新建对象的条件下,将list中指定条件的值去除
package com.liujianwang.learning;import java.util.LinkedList; import java.util.List;public class ListTest {public static void main(String[] args) {/** 在不允许新建对象的条件下,将list中指定条件的值去除。* 例如:移除list中值大于6的元素。…

openlayers map获取全部feature_tf2.0基础-tf.data与tf.feature_column
7.2.1 tf.data使用 tf.data API 可以轻松处理大量数据、不同的数据格式以及复杂的转换。tf.data API 在 TensorFlow 中引入了两个新的抽象类:tf.data.Dataset 表示一系列元素,其中每个元素包含一个或多个 Tensor 对象。:创建来源(…

项目活动定义 概述
项目活动定义概述 项目活动定义是确认和描述项目的特定活动,它把项目的组成要素加以细分为可管理的更小部分,以便更好地管理和控制。 确定计划活动需要确定和记载计划完成的工作。活动定义过程识别处于工作分解结构(WBS)最下层,叫…

如何判断CPU、内存、磁盘的性能瓶颈?
1.如何判断CPU、内存、磁盘的瓶颈? CPU瓶颈 1) 查看CPU利用率。建议CPU指标如下 a) User Time:65%~70% b) System Time:30%~35% c) Idle:0%~5% 如果us,sy高于这个指标可以判断CPU有瓶颈 使用top…

一个苹果手机移动电源也能让他拽得跟二五八万似的
一个苹果手机移动电源也能让他拽得跟二五八万似的~~低调一定是美德,尤其是在见过各种JP人类之后,我真心在心里呐喊,你丫稍微低调一点会死啊!!!是的,这个世界上不可能不存在拽得调子高的人&#…

Confluence 6 配置服务器基础地址
服务器基础地址(Server Base URL)是用户访问 Confluence 的 URL 地址。这个基础的 URL 地址必须与你在浏览器中访问 Confluence 中的地址。 Confluence 将会在安装的时候自动侦测基础的 URL,但是如果你的站点 URL 修改了,或者你的…

python gui编程框架添加工具栏_python gui编程,我是初学者。用tk,制作下拉菜单的command不分我想打开另一个界面。如和解决,求解!!...
展开全部 from tkinter import * def new_file(): print("Open new file") def open_file(): print("Open existing file") def stub_action(): print("Menu select") def makeCommandMenu(): CmdBtn Menubutton(mBar, textButton Commands, un…

这样在一个sql里完成更新和插入,只用一次数据库连接,效率提高了
代码如下,请给出具体修改代码 public void AddCategory(string nCategoryName, int nImgId, int nBelongToId, int nShopId, int nSortId) { int CategoryId 0; string cmdText "Select top 1 CategoryId from ProductCategory where Categ…

USACO Section 1.5 Checker Challenge
经典八皇后问题 只写的最基本的,对称剪枝,位运算都没有用,以后有时间再看 1 /* ID:linyvxi1 2 PROB:checker 3 LANG:C 4 */ 5 #include <stdio.h> 6 #include <stdlib.h> 7 #include <string.h> 8 int N; 9 int tota…

使用JavaScript实现在页面上所有内容加载完之前一直显示loading...页面
Html 1 <body class"is-loading">2 <div class"curtain">3 <div class"loader">4 loading...5 </div>6 </div> 7 <div>8 <!--这里 正文 -->9 </div> 10 </body> …

SpringCloud + Consul服务注册中心 + gateway网关
1 启动Consul 2 创建springcloud-consul项目及三个子模块 2.1 数据模块consul-producer 2.2 数据消费模块consul-consumer 2.3 gateway网关模块 3 测试及项目下载 1、首先安装Consul并启动Consul,端口号为8500 2、创建一个maven项目springcloud-consul࿰…

MySql按日期进行统计(前一天、本周、某一天)[转载]
转自:http://www.yovisun.me/mysql-date-statistics.html 在mysql数据库中,常常会遇到统计当天的内容。例如,在user表中,日期字段为:log_time 统计当天 sql语句为: select * from user where date(log_time…
右键新建里面没有word和excel_Windows10系统下如何将Sublime Text3添加到右键快捷菜单?...
由于本人用的Sublime Text是汉化绿色版的,不仅仅是因为绿色版免去了安装步骤 解压即用,还因为里面整合了常用的高效率必备插件,但是发现右键竟然没有用Sublime Text打开的快捷菜单,这对于我使用Sublime Text 打开一些代码文档会有…

NOI2011 道路修建
题目连接:http://221.192.240.123:8586/JudgeOnline/showproblem?problem_id1670 题意自便。 相关知识:树的遍历,非递归DFS写法。 分析:因为树的边给定,所以从哪个点开始求都是一样的。递归求出每个点的的子树个数&am…

Wiener Filter
假设分别有两个WSS process:$x[n]$,$y[n]$,这两个process之间存在某种关系,并且我们也了解这种关系。现在我们手头上有process $x[n]$,目的是要设计一个LTI系统,使得系统输出$y[n]$,不过$y[n]$是…

c++ string replace_JAVA应用程序开发之String类常用API
【本文详细介绍了JAVA应用开发中的String类常用API,欢迎读者朋友们阅读、转发和收藏!】1 基本概念API ( Application Interface 应用程序接口)是类中提供的接口,类库是类的集合。在 Java 语言中可以通过 import 关键字导入相关的类࿰…

强大的Charles的使用,强大的flutter1.9
<a href"http://www.cocoachina.com/articles/37551?filterios"> 强大的Charles强大的flutter转载于:https://www.cnblogs.com/henusyj-1314/p/11586350.html

多层次架构设计前言
因为 php 原生来就是要辅助 HTML 的产生,所以程式码跟 HTML 码混在一起写,正是 PHP 的特点也是优点,但正也造成很多分工上的问题,也就是你在写 php 的同时,你也必须很了解 前端、后端技能,像是 DataBase, H…
