继承和多态 3.0 -- 菱形继承
单继承和多继承
C++的继承方式是支持单继承和多继承的,首先看一下代码,分清单继承和多继承
单继承
class A
{
public:int _a;
};class B :public A
{
public:int _b;
};class C : public A
{
public:int _c;
};类似于上面的方式就是单继承,或者C类可以不继承A类,而是直接继承B类,这种方式也是单继承
多继承
class D :public B,public C
{
public:int _d;
};上面的这种方式就是多继承,即是D类既继承了B类,又继承了C
通过上一个章节的学习我们知道,继承的时候,在子类的 成员变量里面包含了父类的成员变量,则我们可以分析出,上面的继承 关系中,B类里面包含变量_a,和变量_b;C类里面包含了变量_a和变量_c;这个时候我们的D类里面就包含了B类的成员变量和C类的成员变量,所以D类里面包含的成员变量是_a,_b,_a,_c,_d。
菱形继承
基于上面的分析我们引入了菱形继承,下面我们用一个图来表示上面的成员的关系

菱形继承问题 – 二义性和数据冗余
还是上面的代码,这个时候我们实例化一个D类的对象,这个时候我们想对_a赋值,就会出现报错,请看下面的代码
D d;d._a = 1;return 0;这个时候编译器报的错误就是D::_a不明确,为什么不明确呢,这个从上面的图中可以看出来,因为我们的D类的对象中有有两个_a的成员变量,这个时候对_a赋值的时候,编译器不知道该给哪个_a赋值,这个问题就是====二义性====问题。
首先看下面的解决办法
D d;d.B::_a = 1;通过这种方式我们就不会出现二义性的问题了。
还有一个问题就是,我们的D类型的对象中,有两个_a这个时候的_a表示的意义都是一样的,如果我们的A类里面的成员变量非常的大,这个时候是不是就是==数据冗余==呢,我们需要一个A类的成员就够了。
解决菱形继承 – 虚拟继承
为了解决上面的问题,我们引入了虚拟继承的概念,请看下面的代码
class A
{
public:int _a;
};class B :virtual public A
{
public:int _b;
};class C : virtual public A
{
public:int _c;
};class D :public B,public C
{
public:int _d;
};int main()
{D d;d._a = 1;return 0;
}这个时候在主函数中,再次使用上面的方式对_a赋值的时候,就不会报错了,那么我们不禁想问,编译器到底是如何做的呢,为什么这么做的时候就不会出现问题了呢,这个问题要从C++对象模型说起
虚继承对象模型
下面是普通的继承,没有虚拟继承,我们结合旁边的代码可以看到,如果没有虚拟继承的时候,D类的对象中会为两个A类型里面的_a变量,这就是数据冗余和二义性

下面我们再来看一下如果我们使用的是虚拟继承给赋值的给赋值的时候是什么结果呢,看下面的截图

这个时候我们注意到一个问题是,和刚刚的那个截图不一样的是,在变量_b的上面放置的不是一个变量_a,而是一个类似于一个地址一样的数据,同样的道理,在变量_c的上面放置的也不是变量_a,也是一个地址一样的内容,我们又来发现一个问题就是,我们给变量_a,赋值的地方显示的是在变量_d的下面,然后我们再来看看那个类似于地址一样的内容到底是什么呢
我们把这个类似地址的数据放置放在监视窗口中看一下

这个时候我们看到,监视窗口2里面放置的内存的位置放置的十六进制数是14,转化成十进制就是20,我们再来比较一下监视窗口1中,那个地址和_a实际存放的位置的距离是20,这个时候我们就能够理解了,原来这里放置的是_a这个变量的偏移量。
还有一个疑问就是,为什么监视窗口2中对应的地址上面放置的是0,而不是14呢,这是因为,这个0所在位置是为了给接下来的虚函数准备的,这个以后会讨论到。
这里需要说明的是,监视窗口1中放置的是地址是虚基表指针,它指向的是一个虚基表。
我们还需要考虑的一个问题就是,为什么这里不直接放置_a的地址,而是放置的是相对位置的偏移量呢,这里我们分析这样的一个问题,如果我们拿这个类去实例化多个对象的话,是不是每个对象就有一个存放_a的地址呢,那么这个时候,每个对象的放置的地址都一样了,而如果放置的是偏移量的话,每个对象的地址空间中放置的内容都是一样的,这就减少了计算的开销。
相关文章:

C# split 几种使用方法
第一种方法: string s "abcdeabcdeabcde"; string[] sArray s.Split(c); foreach (string i in sArray) Console.WriteLine(i.ToString()); Console.ReadKey();输出下面的结果:abdeabdeabd…
模糊匹配 读音_onenote搜索机制详解②:两种搜索模式,模糊与精确匹配
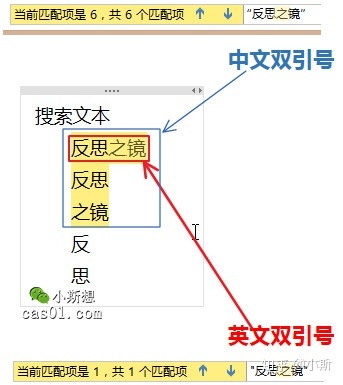
先从纯文本搜索讲起,这是最基本也是最重要的。从这篇开始,以及接下来连续几篇文章,都会介绍搜索的基础功能。注意,这几篇文章中谈论的都是基本的、正常的搜索功能,暂时不考虑Bug等因素。在很多软件(例如wor…

EXT3与EXT4的主要区别
Linux kernel 自 2.6.28 开始正式支持新的文件系统 Ext4。 Ext4 是 Ext3 的改进版,修改了 Ext3 中部分重要的数据结构,而不仅仅像 Ext3 对 Ext2 那样,只是增加了一个日志功能而已。Ext4 可以提供更佳的性能和可靠性,还有更为丰富的…

Java IO 4 : RandomAccessFile
RandomAccessFile: 认识:java输入/输出流体系中功能最丰富的文件内容访问类 既可以读取文件内容,也可以向文件传输数据,并且支持“随机访问“的方式,程序可以跳转到任意地方来读写数据。 特点:与OutputStream/Writ…

二叉树 1.0 -- 创建二叉树、遍历二叉树、二叉树常见问题求解
树的结构主要是为了查找,这个主要是为了搜索,树的结构关注的不是增删查改 树 广义上面的树的结构我们不知道树的一个节点是有几个子节点的,所以这个时候我们需要定义的一种结构就是,一个节点的孩子是可以动态的增加的࿰…

impala 本年格式化时间_hive,hbase,impala之间的对比
hbase在三者中更注重的是存储,它实现了类似mysql的double write机制,但是它是一种NoSQL的数据库,并且是可以支持列式存储的,算是比较大的一个内存Hash表。hbase也采用了类似mysql中的mvcc的思想通过时间戳来做版本控制。hbase是在…

简单上手的游戏引擎
物理游戏引擎 GameSalad 转载于:https://www.cnblogs.com/sgdkg/archive/2013/06/14/3135882.html

Linux内核中关于定时器Timer的应用
2019独角兽企业重金招聘Python工程师标准>>> 在Touchscreen驱动中 1 声明 Ad7877.c (\linux-2.6.30.4\drivers\input\touchscreen): struct timer_list timer; /* P: lock */ 2 初始化 在函数 static int __devinit ad7877_probe(struct spi_device *spi) 中 执行 …
类加载过程中几个重点执行顺序整理
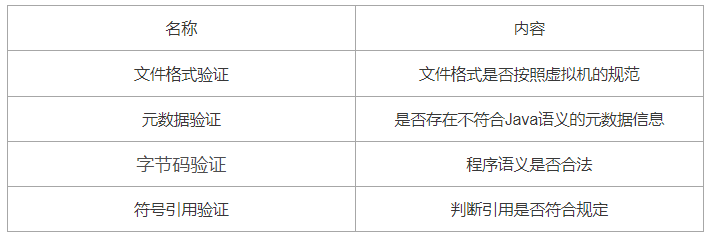
类的加载过程: 1、 JVM会先去方法区中找有没有相应类的.class存在。如果有,就直接使用;如果没有,则把相关类的.class加载到方法区 2、 在.class加载到方法区时,会分为两部分加载:先加载非静态内容ÿ…

二叉树 2.0 -- 非递归遍历
二叉树递归遍历存在的问题 如果我们的二叉树只有左子树,而且树的高度还很深的时候,这个时候递归调用遍历的时候,栈帧空间开辟的较大,很可能造成栈溢出。但是我们一个程序中,为堆分配的空间要比栈大的多,这…
田忌赛马贪心算法_田忌赛马 贪心算法
算法实验课回顾田忌赛马问题描述:你一定听说过田忌赛马的故事吧?如果3匹马变成n匹(n<100),齐王仍然让他的马按照优到劣的顺序初赛,田忌可以按任意顺序选择他的赛马出赛。赢一局,田忌可以得到200两银子;输…

[转][小结][三种方法]实现WPF不规则窗体
实现WPF不规则窗体的三种常用的方法如下: 1.使用Blend等工具绘制一个不规则xaml,然后作为窗体的背景。这个可以参考xiaowei0705的这篇博文:WPF制作不规则的窗体 。 2.给window的Clip属性赋Path值。这个可以参考DebugLZQ前面的博文:…

VirtualBox虚拟机网络连接设置的四种方式
这里我先给大家大致讲解下VBox的网络配置及应用。 VirtualBox的提供了四种网络接入模式,它们分别是:1、NAT 网络地址转换模式(NAT,Network Address Translation)2、Bridged Adapter 桥接模式3、Internal 内部网络模式4、Host-only Adapter 主机…

redis-deskmanager 连不上 虚拟机 - centos redis
1、没设置redis密码 : https://blog.csdn.net/HUXU981598436/article/details/54668779 2、关闭防火墙 转载于:https://www.cnblogs.com/Jomini/p/9650650.html

数据库1.0 -- 数据库的基本操作
安装数据库 安装数据库的时候我们需要安装三个软件,使用下面的命令,可能还会出现一些问题,关于数据库的安装,大家可以上网自行百度 yum install mysql yum install mysql-server yum install mysql-devel 我个人的理解大概是这…

12,缓冲运动。匀速运动停止条件
缓冲运动:iSpeed(iTarget-oDiv.offsetLeft)/7;速度离目标点越远,速度越大,离目标点越近速度越小; 只支持1px是最小单位,没有0.5px。所以当iSpeed为小数时如(0.7),oDiv.style.LeftoDi…
如何配置mac的mysql环境_mac安装mysql数据库及配置环境变量
安装mysql下载mysql。我下载的是:mysql-8.0.11-macos10.13-x86_64.dmg双击打开mysql-8.0.11-macos10.13-x86_64.dmg,然后双击mysql-8.0.11-macos10.13-x86_64.pkg一路点击继续,傻瓜式安装,没什么好说的此处选择“Use Legacy Passw…

三层交换机vlan间访问(第一种方式)
真的是原创,但是得感谢Ys_routesim软件的制作方。我将命令调试后并进行了解释。若是属于侵权,请立即告知我。不过学习了网工后,大段解读源代码不属于侵权吧。呵呵。 交换机的三层交换实际是具有路由功能的交换机,比如思科的Cisco …

(转载)深入浅出设计模式——桥接模式(Bridge Pattern)
模式动机设想如果要绘制矩形、圆形、椭圆、正方形,我们至少需要4个形状类,但是如果绘制的图形需要具有不同的颜色,如红色、绿色、蓝色等,此时至少有如下两种设计方案: 第一种设计方案是为每一种形状都提供一套各种颜色…

数据库2.0 -- 数据类型和数据表的基本操作
mysql支持多种数据类型,一般可以分为,数值,日期时间和字符(串) 数值类型 日期和时间类型 字符串类型 创建数据表 我们首先应该明白的就是一个结构的问题,一个用户可以管理多个数据库,每个数据…

virtual hust 2013.6.20 数论基础题目 D - Just the Facts
题目:Just the Facts 思路:枚举10000素数内,各因子出现的次数,然后取模为10。因为0是由2和5构成的,所以2和5的幂单独讨论,同时由于2的幂肯定大于5的,所以我们最后要算的再乘上2的减去后的幂就可…

MySQL中字段约束有哪些_mysql字段约束
为了确保数据的完整性和唯⼀性,关系型数 据库通过约束机制来实现目。一. unique 唯一性约束值不可重复;二. not null 非空约束值不可为空;三. default 默认值约束当增加数据时没有插⼊值时,会自动插⼊默认值;四. chec…

关于软件测试中那点小事中的大道理
如果想让测试在公司的项目中发挥出它最大的价值,并不是招两个测试技术高手,或引入几个测试技术,而是测试技术对项目流 程的渗透,以及测试流程的改进与完善。虽然,当然测试行业前景乐观,许多中小企业也都在引…

每日一题 -- 11-1
一天十题选择,一天一道编程,一天一个面试题,一个一个剑指offer 排序是必须要掌握的一个算法,非常的重要 题目描述 有 n 个学生站成一排,每个学生有一个能力值,牛牛想从这 n 个学生中按照顺序选取 k 名学…

Java中? extends T和? super T的理解
? 通配符类型 - <? extends T> 表示类型的上界,表示参数化类型的可能是T 或是 T的子类; <? super T> 表示类型下界(Java Core中叫超类型限定),表示参数化类型是此类型的超类型(父类型)&…

学习Modern UI for WPF
这两天断断续续的学了学Modern UI for WPF 没啥学习笔记呵呵,来自大牛王春明的博客园 http://www.cnblogs.com/wangchunming/category/342887.html 此大牛学习范围之广 成果之丰富 着实是学习的典范转载于:https://www.cnblogs.com/DragonX/p/3146818.html

idea的tomcat配置文件在哪里修改_MyBatis配置文件详解
MyBatis 的配置文件包含了会影响 MyBatis 行为的设置和属性信息,决定了mybatis的运行轨迹,能充分了解这些配置的以及配置所带来的的影响,你就是大神!配置文件的根节点是configuration,他的子孙节点有:prope…

《几何与代数导引》例1.4——定比分点
点$r$分有向线段$\vec{pq}$成定比$k$,即$\vec{pr}k\vec{rq}(k\neq-1)$.在仿射标架中,已知$p(a_1,a_2,a_3)$,$q(b_1,b_2,b_3)$和$k$,求$r(c_1,c_2,c_3)$解:由于$c_i-a_ik(b_i-c_i)$,因此$c_i\frac{kb_ia_i}{1k}$.转载于:https://www.cnblogs.com/yeluqing/archive/20…
C#第一个程序Helloworld
转载于:https://www.cnblogs.com/gzhbk/p/9656149.html

Leanote
https://github.com/leanote/leanote/wiki/Leanote-%E4%BA%8C%E8%BF%9B%E5%88%B6%E7%89%88%E8%AF%A6%E7%BB%86%E5%AE%89%E8%A3%85%E6%95%99%E7%A8%8B—-Mac-and-Linux 安装的网址 我们相当于是在本地建立了一个服务器,然后将我们的leanote部署上去了 我们这里的启…
