图很难理解?看这篇图论基础与图存储结构就够了
 点击上方↑↑↑蓝字关注我们~
点击上方↑↑↑蓝字关注我们~
「2019 Python开发者日」,购票请扫码咨询 ↑↑↑
作者 | 程序员吴师兄
转载自五分钟学算法(ID:CXYxiaowu)
1 前言
打算先普及一下图的相关理论支持,本文不建议一口气阅读完毕,可以先浏览一遍,在后续有需要的时候进行查阅即可。
2 图
图是数据结构中重要内容。相比于线性表与树,图的结构更为复杂。在线性表的存储结构中,数据直接按照前驱后继的线性组织形式排列。在树的结构中,数据节点以层的方式排列,节点与节点之间是一种层次关系。但是,在图的结构中数据之间可以有任意关系,这就使得图的数据结构相对复杂。
2.1 定义
定义:图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
例如:图 2.1 所示图
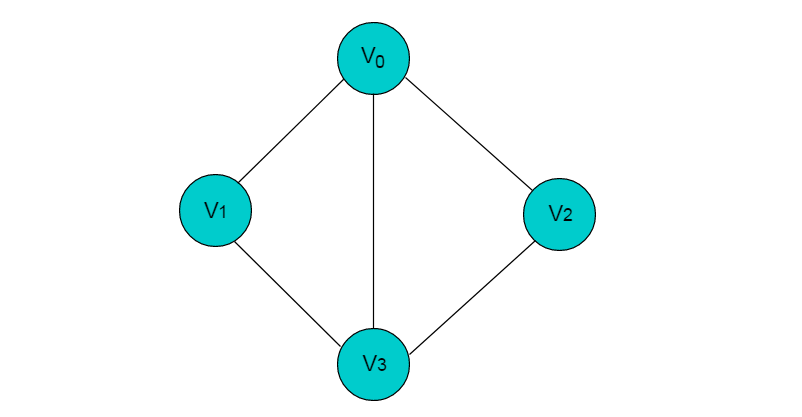
图2.1
在图 2.1 中,共有 V0,V1,V2,V3 这 4 个顶点,4 个顶点之间共有 5 条边。
注:
当线性表没有数据节点时,线性表为空表。
树中没有节点时,树为空树。
但是,在图中不允许没有顶点,但是可以没有边。
2.2 无向边
无向边:若顶点 x 和 y 之间的边没有方向,则称该边为无向边(x,y),(x,y) 与 (y,x) 意义相同,表示 x 和 y 之间有连接。
图 2.2 所示图中的边均为无向边。
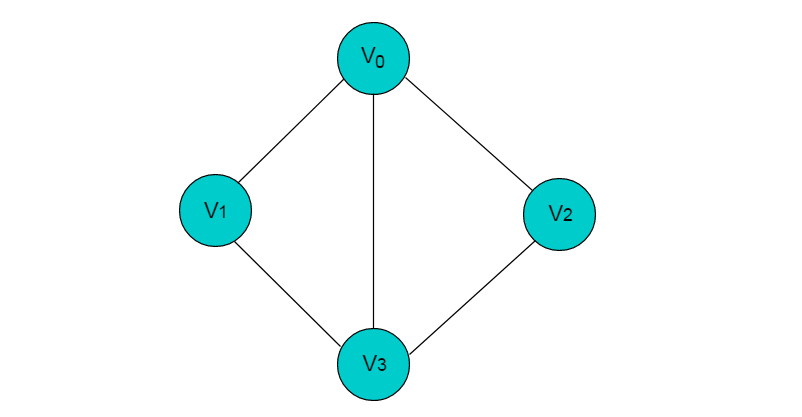
图2.2
2.3 有向边
有向边:若顶点 x 和 y 之间的边有方向,则称该边为有向边,与表示的意义是不同的,表示从 x 连接到 y ,x 称为尾,y 称为头。表示从 y 连接到 x ,y 称为尾, x 称为头。
图2.3所示图中的边为有向边。
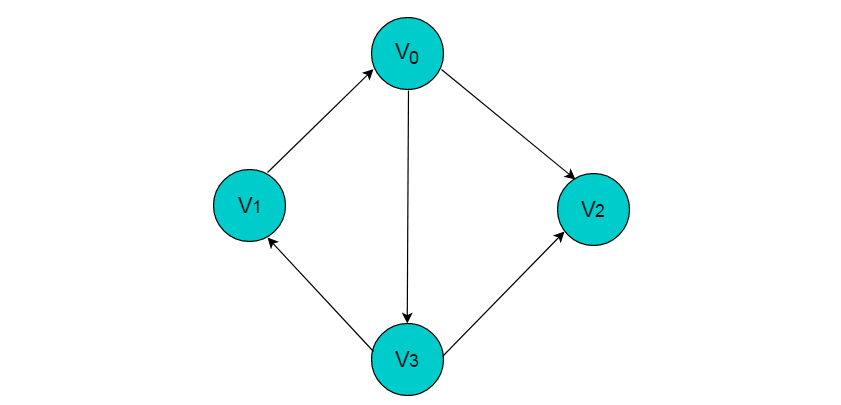
图2.3
2.4 无向图
无向图:若图中任意两个顶点之间的边均是无向边,则称该图为无向图。
图2.2所示图为无向图。
2.5 有向图
有向图:若图中任意两个顶点之间的边均是有向边,则称该图为有向图。
图2.3所示的图为有向图。
2.6 顶点与顶点的度
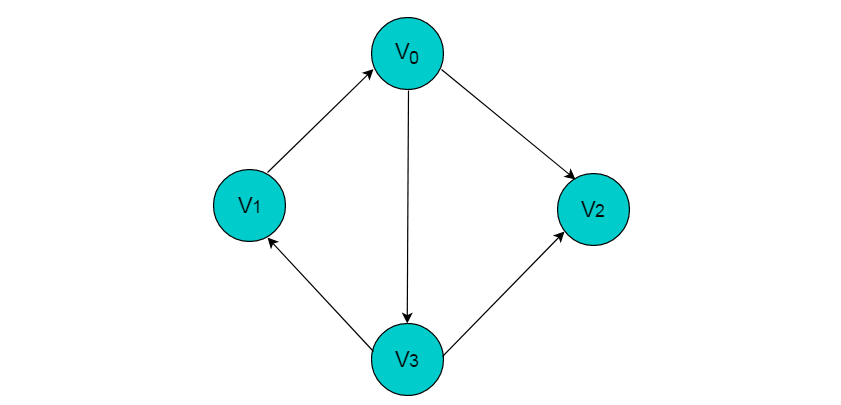
图2.6
顶点的度:
顶点 V 的度是和 V 相关联的边的数目,记为TD(V)。
图 2.6 所示图中,V0 顶点的度为 3 。
入度:
以顶点v为头的边的数目,记为ID(V)。
图2.6所示图中,V0的入度为1。
出度:
以顶点 v 为尾的边的数目,记为 OD(V)。
图2.6所示图中,V0的出度为2。
顶点的度 = 入度 + 出度。
即 TD(V) = ID(V) + OD(V)。
2.7 邻接
邻接是两个顶点之间的一种关系。如果图包含(u,v),则称顶点 v 与顶点 u 邻接。在无向图中,这也暗示了顶点 u 也与顶点 v 邻接。换句话说,在无向图中邻接关系是对称的。
2.8 路径
路径:在图中,依次遍历顶点序列之间的边所形成的轨迹。
例如:在图 2.8 中所示图中依次访问顶点 V0 、V3 和 V2 ,则构成一条路径。
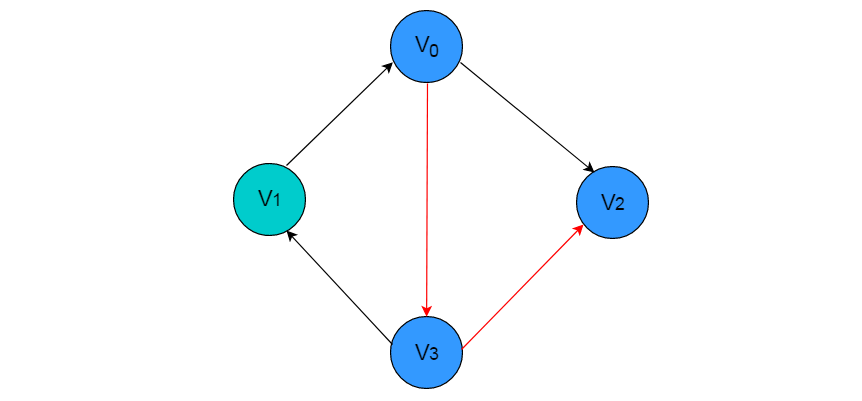
图 2.8
3 完全图
完全图:每个顶点都与其他顶点相邻接的图。
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。(含有n个顶点的无向完全图有(n×(n-1))/2条边)
图 3.1 所示的图为无向完全图。
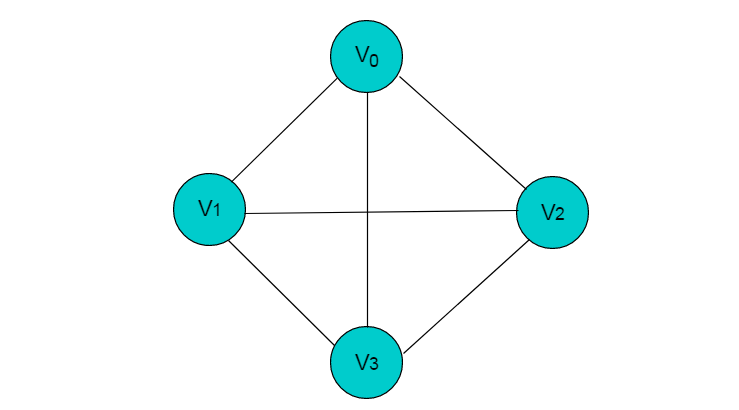
图3.1
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条边,则称该图为有向完全图。(含有 n 个顶点的有向完全图有 n×(n-1) 条边)
图3.2所示的图为有向完全图。
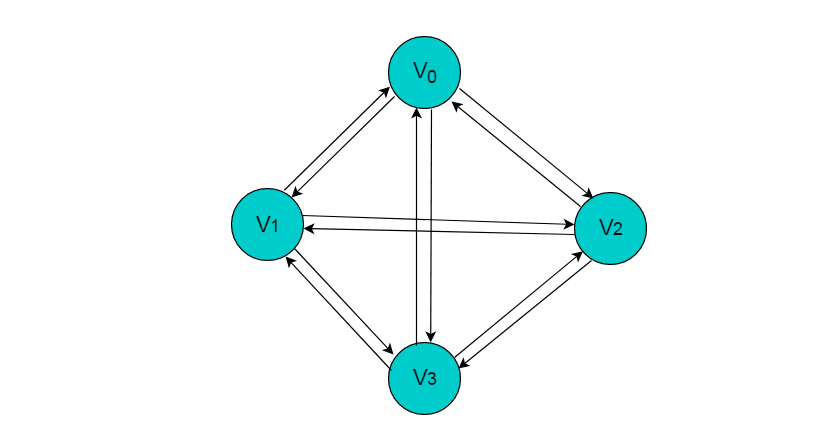
图3.2
4 连通图
在无向图 G 中,如果从顶点 v 到顶点 v' 有路径,则称 v 和 v' 是连通的。 如果对于图中任意两个顶点 vi 、vj ∈E, vi,和vj都是连通的,则称 G 是连通图,否则图为非连通图。
例如:图4.1所示图,图中顶点A、B、C、D是连通的,但是其中任一顶点与顶点E或者顶点F之间没有路径,因此图4.1中所示的图为非连通图。
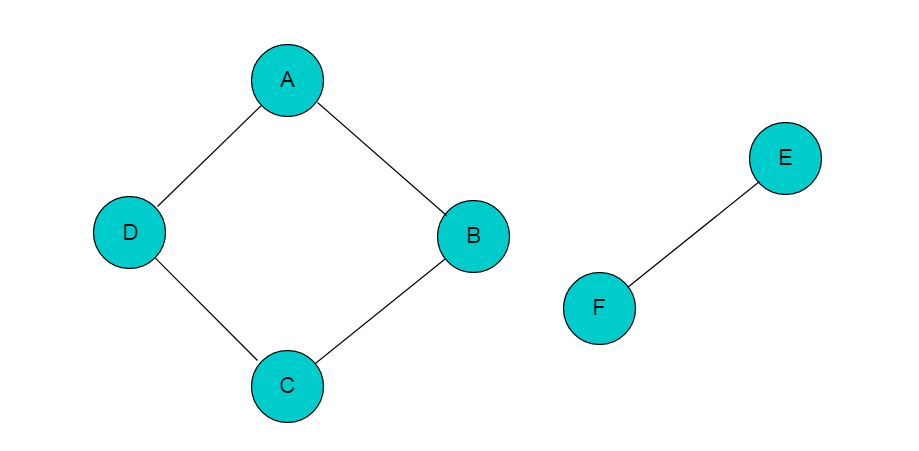
图4.1
若添加顶点B与顶点F之间的邻接边,则图变为连通图,如图4.2所示:
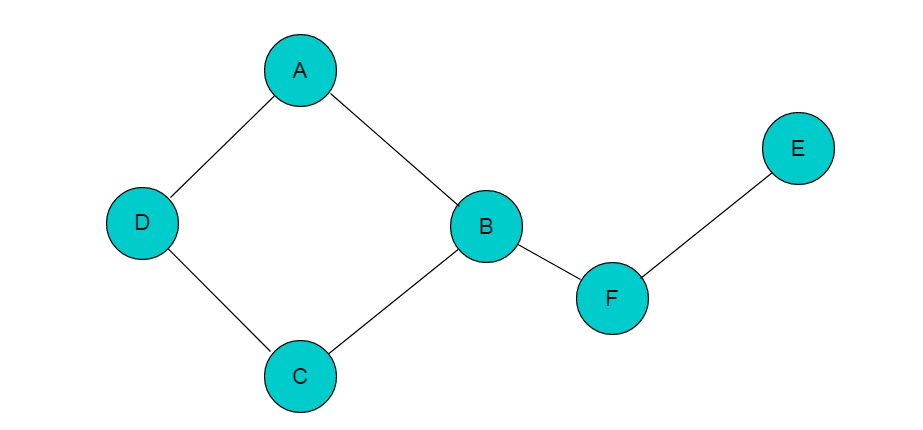
图4.2
5 数组存储
图的数组存储方式也称为邻接矩阵存储。图中的数据信息包括:顶点信息和描述顶点之间关系的边的信息,将这两种信息存储在数组中即为图的数组存储。
首先,创建顶点数组,顶点数组中存储的是图的顶点信息,采用一维数组的方式即可存储所有的顶点信息。存储图中边的信息时,由于边是描述顶点与顶点之间关系的信息,因此需要采用二维数组进行存储。
定义:设图 G 有 n 个顶点,则邻接矩阵是一个n X n的方阵A,定义为:

图 5
其中,或者(Vi , Vj,)表示顶点 Vi 与顶点 Vj 邻接。wi,j表示边的权重值。
例如:下图所示的无向图,采用数组存储形式如下。
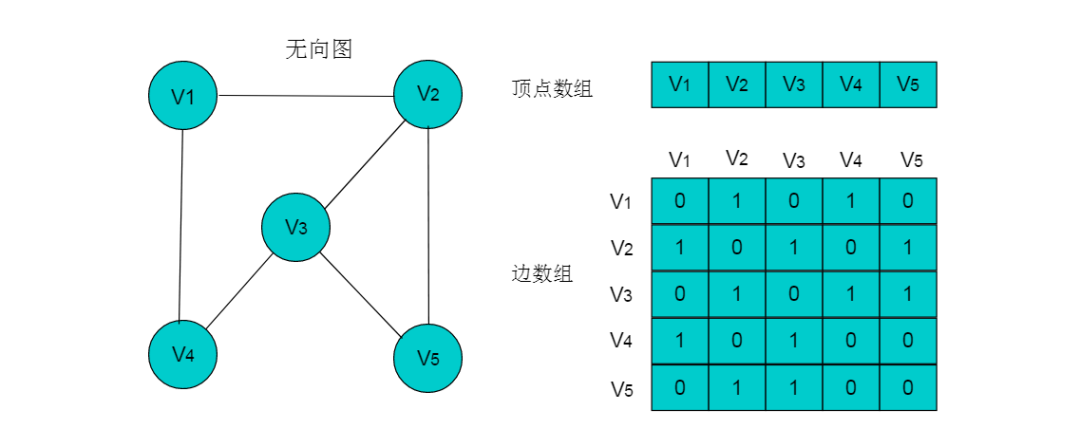
注:图中的数组存储方式简化了边的权值为 1 。
无向图的数组存储主要有以下特性:
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,A[i][j] =1代表顶点i与顶点j邻接,A[i][j] = 0代表顶点i与顶点j不邻接。
(3)在无向图中。由于边是无向边,因此顶点的邻接关系是对称的,边数组为对称二维数组。
(4)顶点与自身之间并未邻接关系,因此边数组的对角线上的元素均为0。
(5)顶点的度即为顶点所在的行或者列1的数目。例如:顶点V2的度为3,则V2所在行和列中的1的数目为3。
当图为有向图时,图的数组存储方式要发生变化。
例如:图5.2所示的有向图,采用数组存储形式如下。
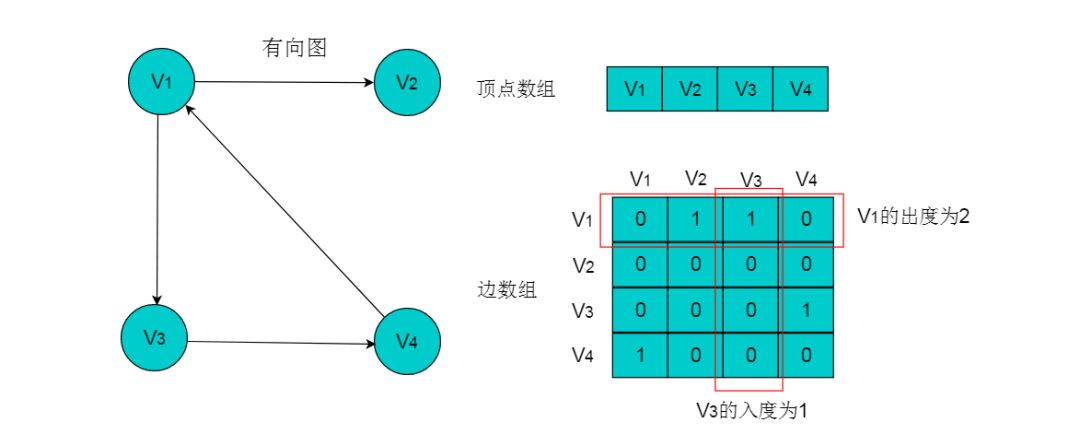
有向图的数组存储主要有以下特性:
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,数组元素为1,即A[i][j] = 1,代表第i个顶点与第j个顶点邻接,且i为尾,j为头。 A[i][j] = 0代表顶点与顶点不邻接。
(3)在有向图中,由于边存在方向性,因此数组不一定为对称数组。
(4)对角线上元素为0。
(5)第i行中,1的数目代表第i个顶点的出度。例如:顶点V1的出度为2,则顶点V1所在行的1的数目为2。
(6)第j列中,1的数目代表第j个顶点的入度。例如:V3的入度为1,则V3所在列中1的数目为1。
数组存储方式优点:
数组存储方式容易实现图的操作。例如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
数组存储方式缺点:
采用数组存储方式,图若有n个顶点则需要n2个单元存储边(弧),空间存储效率为O(n2)。 当顶点数目较多,边数目较少时,此时图为稀疏图,这时尤其浪费空间。
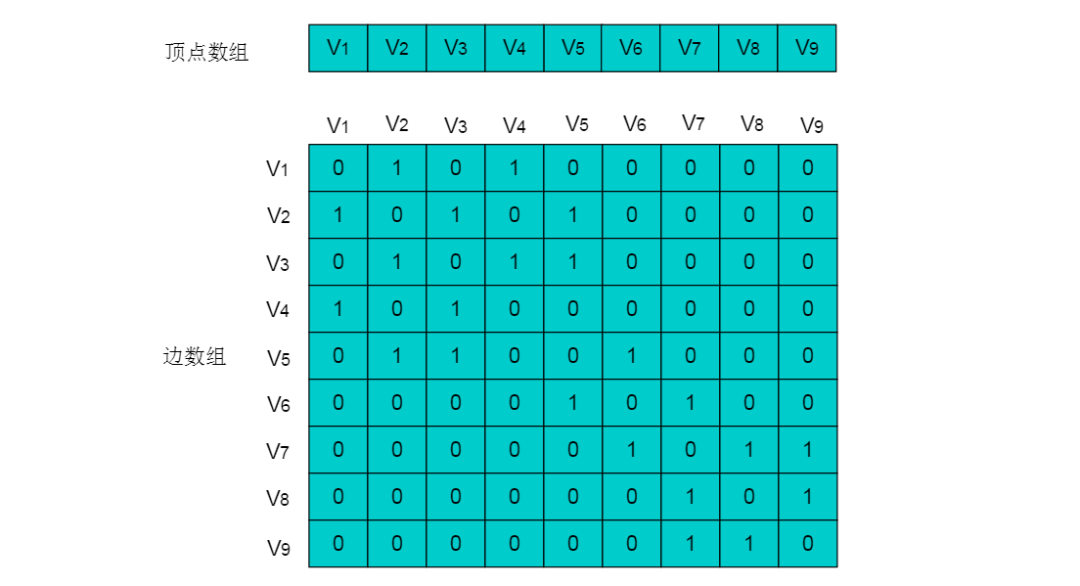
例如:图5.3所示的图,图中有 9 个顶点,边数为10,需要 9X9 的二维数组,而实际存储边信息空间只有10,造成空间浪费。
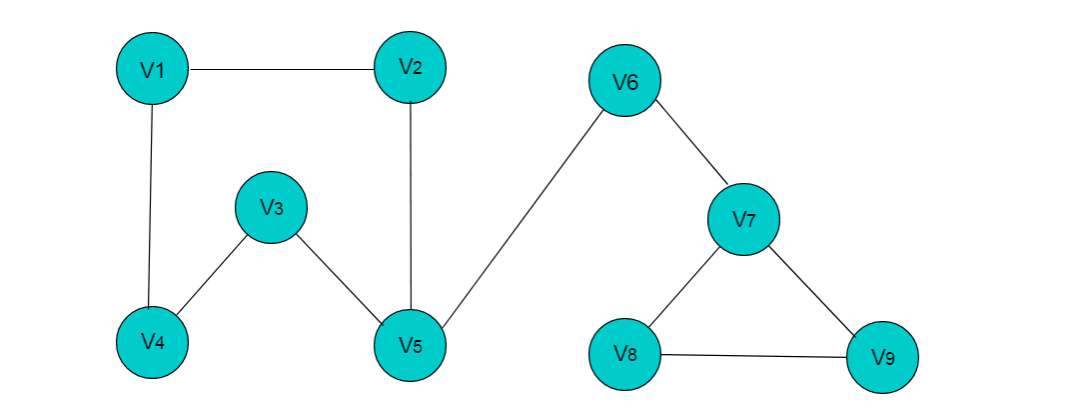
图5.3
图5.3所示无向图的存储数组:
6 邻接表
当使用数组存储时,主要有以下三个问题:
(1)对于一个图,若图中的顶点数目过大,则无法使用邻接矩阵进行存储。因为在分配数组内存时可能会导致内存分配失败。
(2)对于某些稀疏图(即顶点数目多,边数目少),创建的数组大小很大,而真正存储的有用信息又很少,这就造成了空间上的浪费。
(3)有时两个点之间不止存在有一条边,这是用邻接矩阵就无法同时表示两条以上的边。
针对以上情况,提出了一种特殊的图存储方式,让每个节点拥有的数组大小刚好就等于它所连接的边数,由此建立一种邻接表的存储方式。
邻接表存储方法是一种数组存储和链式存储相结合的存储方法。在邻接表中,对图中的每个顶点建立一个单链表,第 i 个单链表中的结点依附于顶点 Vi 的边(对有向图是以顶点Vi为尾的弧)。链表中的节点称为表节点,共有 3个域,具体结构见下图:
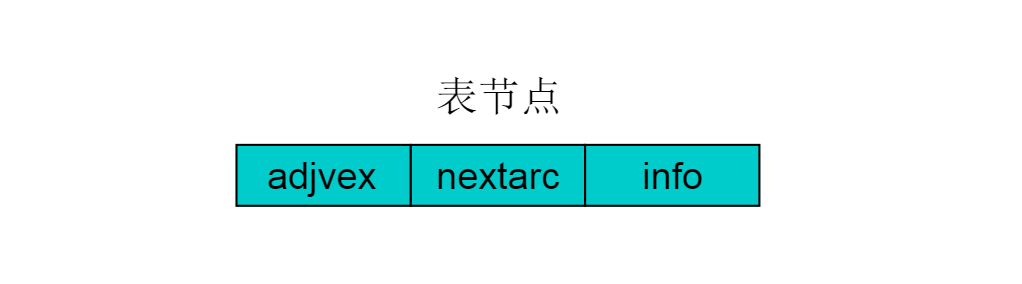
图 6
表结点由三个域组成,adjvex存储与Vi邻接的点在图中的位置,nextarc存储下一条边或弧的结点,data存储与边或弧相关的信息如权值。
除表节点外,需要在数组中存储头节点,头结点由两个域组成,分别指向链表中第一个顶点和存储Vi的名或其他信息。具体结构如下图:
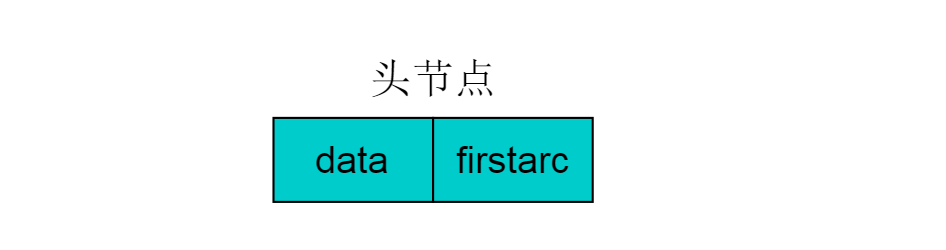
图 6.0
其中,data域中存储顶点相关信息,firstarc指向链表的第一个节点。
无向图采用邻接表方式存储
例如:图6.1所示的无向图采用邻接表存储。
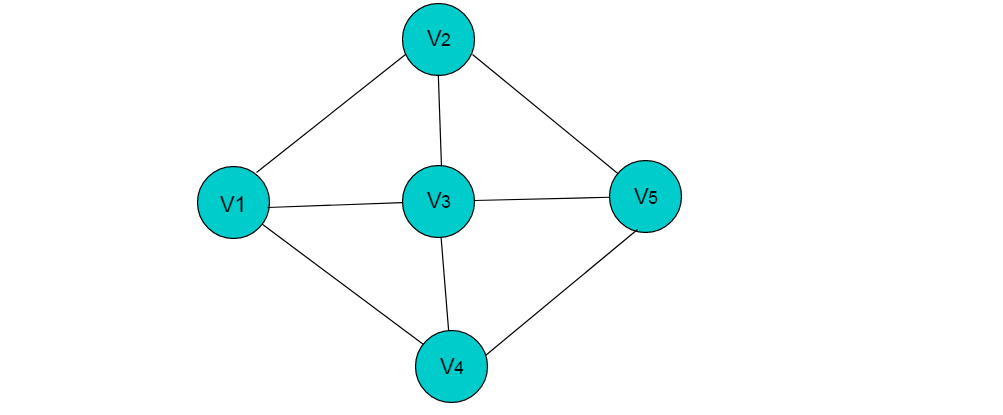
图6.1 无向图
采用邻接表方式存储图 6.1 中的无向图,绘图过程中忽略边节点的info信息,头结点中的 data 域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,则可以创建3个表节点,表节点中adjvex分别存储V2、V3、V4的索引1、2、3,按照此方式,得到的邻接表为:
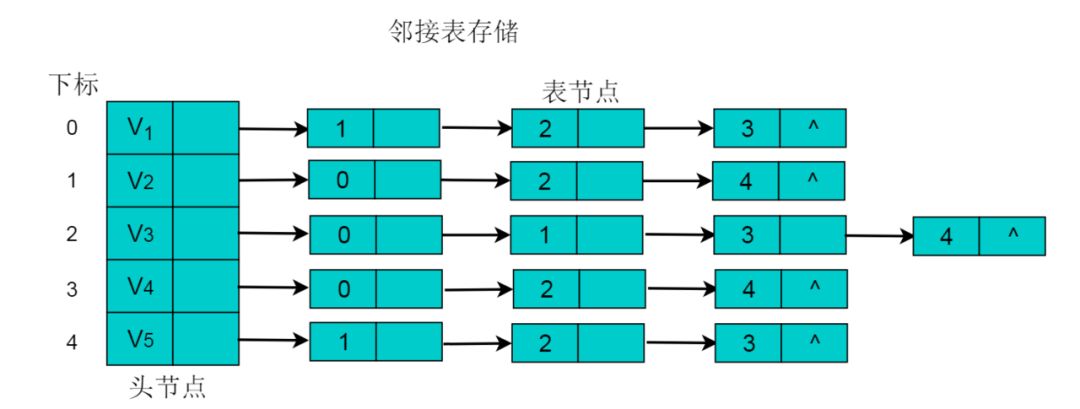
无向图的邻接表存储特性:
(1)数组中头节点的数目为图的顶点数目。
(2)链表的长度即为顶点的度。例如:V1顶点的度为3,则以V1为头节点的链表中表节点的数目为3。
有向图采用邻接表方式存储
例如:图 6.3 所示的有向图采用邻接表存储。
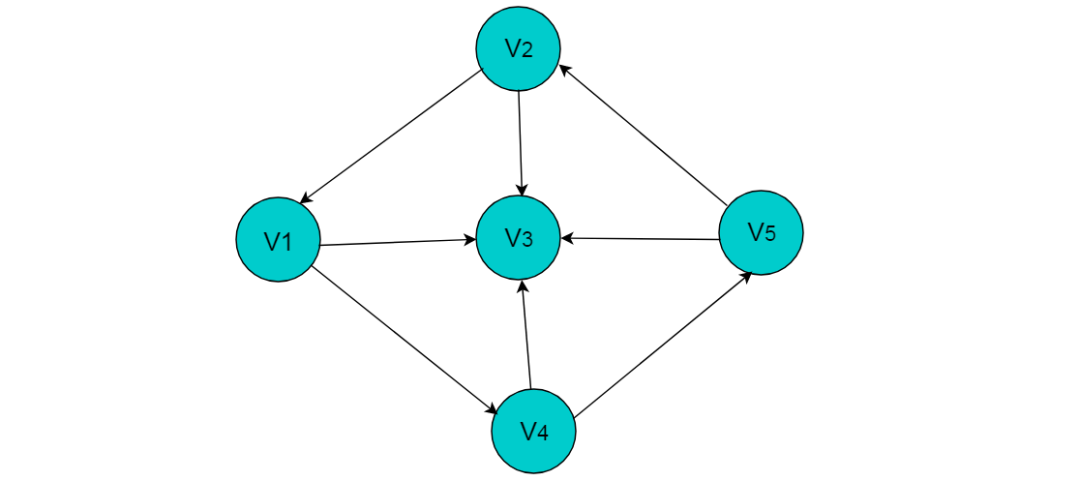
采用邻接表方式存储图6.3中的有向图,绘图过程中忽略边节点的info信息,头结点中的data域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,但是以V1顶点为尾的边只有两条,即和因此,创建2个表节点。表节点中adjvex分别存储V3、V4的索引2、3,按照此方式,得到的邻接表为:
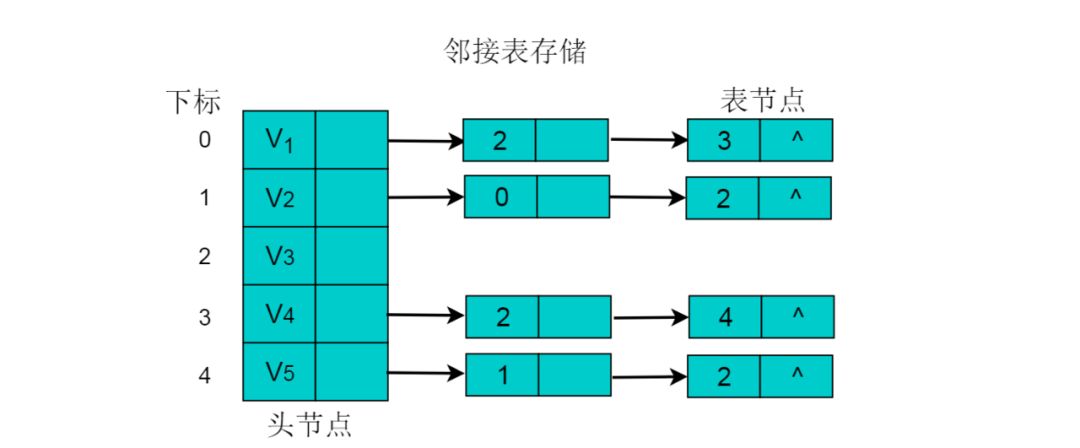
有向图的邻接表存储特性:
(1)数组中表节点的数目为图的顶点数目。
(2)链表的长度即为顶点的出度。例如V1的出度为2,V1为头节点的链表中,表节点的数目为2。
(3)顶点Vi的入度为邻接表中所有adjvex值域为i的表结点数目。例如:顶点V3的入度为4,则链表中所有adjvex值域为2的表结点数目为4。
注:图采用邻接表的方式表示时,其表示方式是不唯一的。这是因为在每个顶点对应的单链表中,各边节点的链接次序可以是任意的,取决于建立邻接表的算法以及边的输入次序。
7 逆邻接表
在邻接表中,可以轻易的得出顶点的出度,但是想要得到顶点的入度,则需要遍历整个链表。为了便于确定顶点的入度,可以建立有向图的逆邻接表。逆邻接表的建立与邻接表相反。
采用逆邻接表的方式存储图3.2所示的无向图。以V3顶点为例,V3顶点的邻接顶点为V1、V2、V4、V5,以V3顶点为头的边有4条,即、、、因此,创建4个表节点。表节点中adjvex分别存储V0、V1、V3、V4的索引0、1、3、4,按照此方式,得到的逆邻接表为:
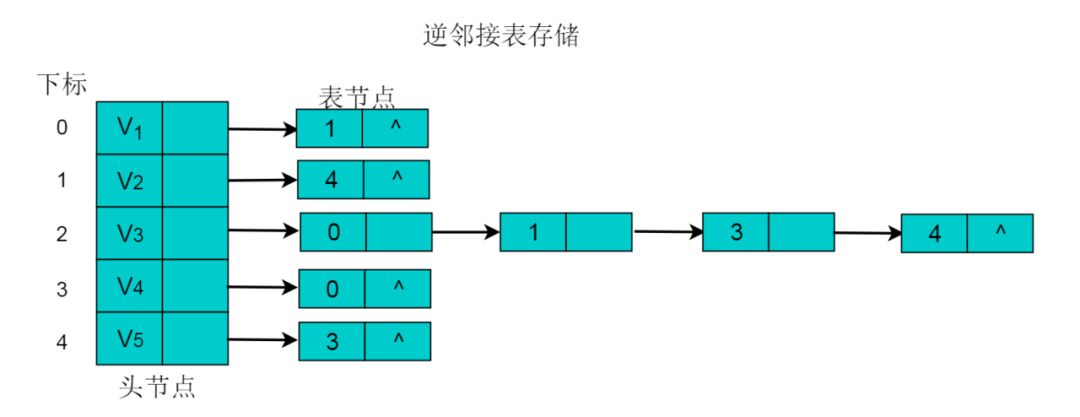
8 十字链表
对于有向图而言,邻接链表的缺陷是要查询某个顶点的入度时需要遍历整个链表,而逆邻接链表在查询某个顶点的出度时要遍历整个链表。为了解决这些问题,十字链表将邻接链表和逆邻接链表综合了起来,而得到的一种十字链表。在十字链表中,每一条边对应一种边节点,每一个顶点对应为顶点节点。
顶点节点
顶点节点即为头节点,由3个域构成,具体形式如下:

图 8
其中,data域存储与顶点相关的信息,firstin和firstout分别指向以此顶点为头或尾的第一个边节点。
边节点
在边节点为链表节点,共有 5 个域,具体形式如下:

img
其中,尾域tailvex和头域headvex分别指向尾和头的顶点在图中的位置。链域hlink指向头相同的下一条边,链域tlink指向尾相同的下一条边。info 存储此条边的相关信息。
例如:图8.1所示的有向图,采用十字链表存储图方式。
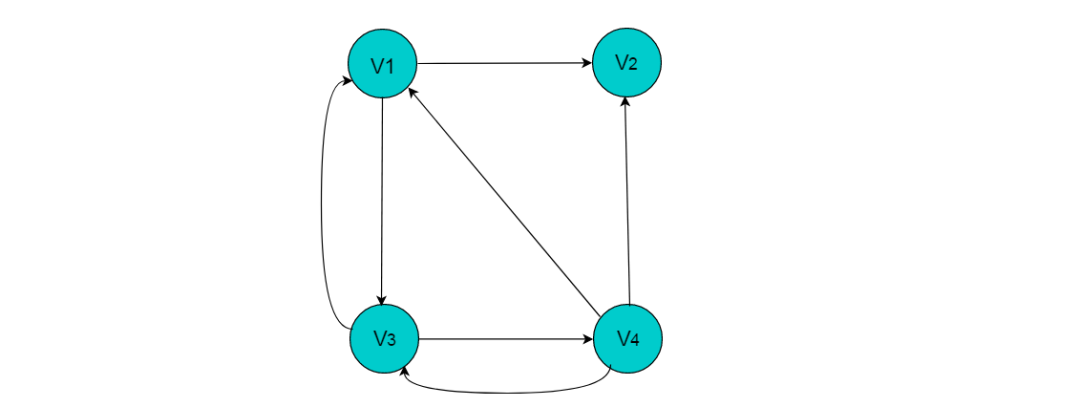
图8.1 有向图
采用十字链表的方式存储图8.1中的有向图,绘图过程忽略边节点中的info信息,表头节点中的data域存储顶点名称。以V1顶点为例,顶点节点的data域存储V1顶点名,firstin存储以V1顶点为头第一个边节点,以V1顶点为头边为,firstout存储以以V1顶点为尾第一个边节点,对应边为。按照此规则,得到的十字链表存储为:
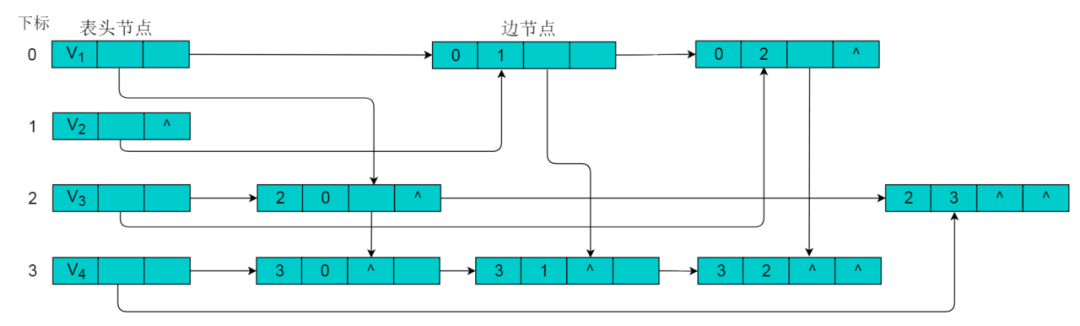
img
注:采用十字链表存储时,表头节点仍然使用数组存储,采用下标索引方式获取。
9 邻接多重表
对于无向图而言,其每条边在邻接链表中都需要两个结点来表示,而邻接多重表正是对其进行优化,让同一条边只用一个结点表示即可。邻接多重表仿照了十字链表的思想,对邻接链表的边表结点进行了改进。
重新定义的边结点结构如下图:

img
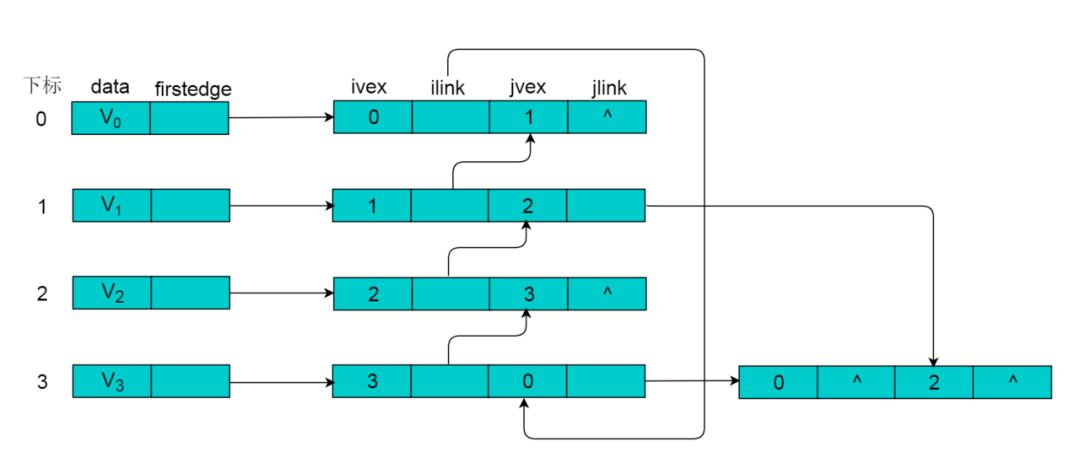
其中,ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。 ilink指向依附顶点ivex的下一条边,jlink指向依附顶点jvex的下一条边。info存储边的相关信息。
重新定义的顶点结构如下图:
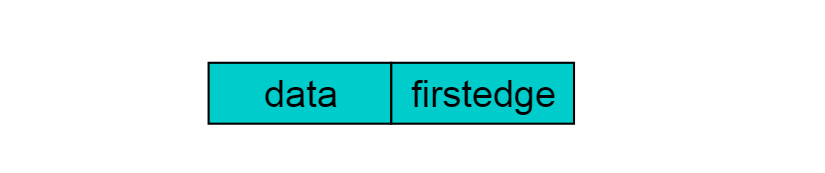
其中,data存储顶点的相关信息,firstedge指向第一条依附于该顶点的边。
例如:图9.1所示的无向图,采用邻接多重表存储图。
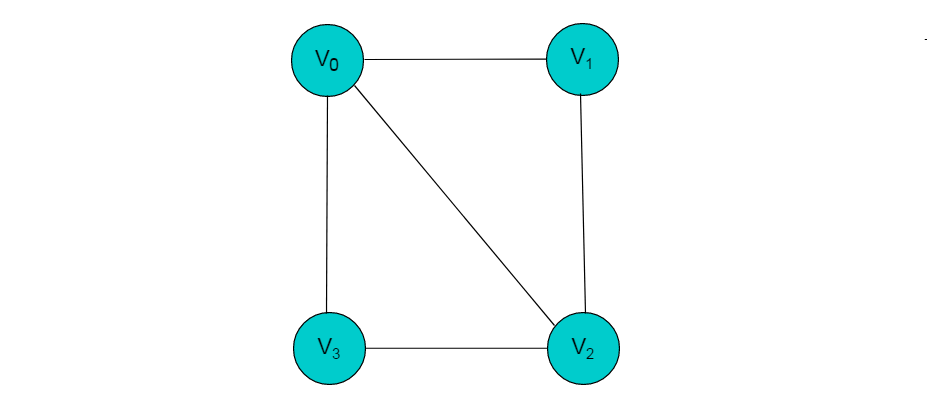
图 9.1 所示的无向图,采用邻接多重表存储,以 V0 为例,顶点节点的data域存储V0名称,firstedge 指向(V0 , V1)边,边节点中的ilink指向依附V0顶点的下一条边(V0 , V3),jlink指向依附V1顶点的下一条边(V1 , V2),按照此方式建立邻接多重表:
(本文为 AI大本营转载文章,转载请联系原作者)
◆
精彩推荐
◆
「2019 Python开发者日」,这一次我们依然“只讲技术,拒绝空谈”10余位一线Python技术专家共同打造一场硬核技术大会。更有深度培训实操环节,为开发者们带来更多深度实战机会。更多详细信息请咨询13581782348(微信同号)。

推荐阅读:
深度 | 人工智能究竟能否实现?
何恺明等人提TensorMask框架:比肩Mask R-CNN,4D张量预测新突破
Python爬取394452条《都挺好》弹幕数据,发现弹幕比剧还精彩?
儿科医生的眼泪,全被数据看见了
程序员怒了!你敢削减专利奖金,我敢拒绝提交代码!
趣挨踢 | 用大数据扒一扒蔡徐坤的真假流量粉
姚期智提出的"百万富翁"难题被破解? 多方安全计算MPC到底是个什么鬼?
程序媛报告:调查了12,000名女性开发者发现,女性比男性更懂Java!
靠找Bug赚了6,700,000元!他凭什么?

你也可以点击阅读原文,查看大会详情。
相关文章:

【Linux】修改/etc/fstab时参数设错,导致启动异常,无法进入系统(已解决)
1、问题描述 在ubuntu14.04上设置自动挂载硬盘分区时,修改/etc/fstab时,将defaults错误写成default,导致启动异常,无法进入系统。 2、解决方法 1)ubuntu启动时有两种模式:普通模式(ubuntu&am…
gitlab安装
根据官方文档安装:https://www.gitlab.com.cn/installation/#centos-6 centos6: 1、没有安装lokkit,yum search lokkit后安装lokkit sudo yum install -y curl policycoreutils-python openssh-server cronie sudo lokkit -s http -s ssh2、安…

如何将Android带入互联网数字家庭? 第一篇转载
前言:很有幸通过ARM Group认识了 ARM的家庭软件架构师 --- 章立(Leon Zhang) (他也是ARM战略软件联盟部门的一员. Leon 拥有多年产品开发和项目管理经验, 曾经参与了数字录像机、机顶盒、数字电视,网络电视以及智能电视࿰…

【linux】用过的shell命令
1、批量替换文件中的字符串 eg:将当前目录 . 下的old替换成new sed -i "s/new/old/g" grep old -rl .如果字符串中有‘/’等特殊字符需要反斜杠‘\’来转移 eg:将当前目录下的“old/old”,替换成“new/new” sed -i "s/new…

node简单实现excel文件下载
1.利用csv格式兼容实现 csv是一种利用,、\t、\n等分隔符存储的文本文件,excel可兼容打开,利用此原理,代码实现如下: app.use(route.get(/export, async ctx > {ctx.res.setHeader(Content-Type, application/vnd.ms-execl);ctx…

儿科医生的眼泪,全被数据看见了
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」,购票请扫码咨询 ↑↑↑作者 | AlfredWu来源 | Alfred数据室(ID:Alfred_Lab)《人间世》第二季第8集《儿科医生:坚守,还是逃离?》把儿科医生的辛苦与挣扎…

[毕业生的商业软件开发之路]C#类型样式
近期开始接触到在校学生、高校实习生和毕业生,在此说一下笔者对这些徘徊在职场门口的学生一些建议,希望能给这些初学者进入软件开发行业带来一些帮助,使得毕业生能更顺利的进入软件开发公司开始职场生涯,人生来一个完美的转弯。 -----------------------…

特斯拉被曝储存大量未加密个人数据 | 极客头条
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」,购票请扫码咨询 ↑↑↑编译丨王哲来源丨猎云网( ID:ilieyun)编者按:特斯拉是否明确界定了数据安全的目标?它现有的规则又在保护哪些人?如果…

【Linux】neocomplcache disabled: “sudo vim“ is detected and $HOME is set to your user‘s home
1、问题描述 使用sudo vim时,弹出提示: neocomplcache disabled: "sudo vim" is detected and $HOME is set to your users home. You may want to use the sudo.vim plugin, the "-H" option with "sudo" or set alwa…

016 | 漫谈区块链共识机制
原创文章,转载请注明:转载自Keegan小钢 并标明原文链接:http://keeganlee.me/post/blockchain/20180425 微信订阅号:keeganlee_me 写于2018-04-25 专栏地址:xiaozhuanlan.com/fullstack 共识机制是区块链的一个核心特征…

临危不乱,.Net+IIS环境经常出现的问题及排障。
http://www.cnblogs.com/CoreCaiNiao/archive/2011/08/02/2123991.html

零门槛!手把手教你打造AI应用
如你所见,聊天机器人已经逐渐渗透到生活的方方面面。它可以提供生活娱乐方面的服务,比如查询音乐、地图、天气,做心理测试,甚至 Google 的 Duplex 技术还能让你通过机器人进行订餐,当然还有很多能跟你谈天说地闲聊胡扯…

【Qt】启动QtCreator时报错:Cannot mix incompatible Qt library (version ) with this library (version...
1、问题描述 当启动QtCreator时报错(我的Qt版本是Qt5.6.3): Cannot mix incompatible Qt library (version 0x50603) with this library (version 0x50601) Aborted (core dumped)2、原因分析 原因是QtCreator使用的Qt库版本是5.6.1,而环境中配置的Qt库版本是5.6.3 1)Q…

利用IIS作为宿主 发布你的WCF Service(转)
http://blog.csdn.net/blacksource/article/details/3942130最近公司的一个需求,涉及到WCF开发。在网上找了些资料,大都是利用单独的应用程序、或者Windows服务作为WCF Service的host。其实WCF还提供一种方式,和以前的Remoting比较类似&#…

旷视提出AutoML新方法,在ImageNet取得新突破 | 技术头条
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」,购票请扫码咨询 ↑↑↑来源 | 旷视研究院 近日,来自旷视研究院的郭梓超、张祥雨、穆皓远、孙剑等人发表一篇新论文“Single Path One-Shot Neural Architecture Search with Uniform Sampling”&a…
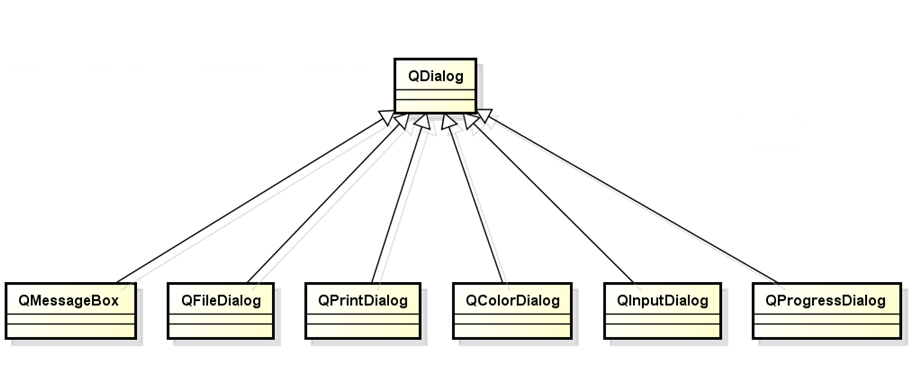
9.QT-标准对话框
Qt提供的可复用的标准对话框,全部继承自QDialog类,如下图所示: QMessageBox:信息对话框,用于显示信息、询问问题等;QFileDialog:文件对话框QColorDialog:颜色对话框QInputDialog:输入对话框(允许用户输入一…

【Python】解决print不能立即打印的问题
1、问题描述 在Python中使用print打印hello world时,终端不显示 def hello():print("hello world!")2、原因 因为标准输入输出stdin/stdout有缓冲区,所以使用print不能立即打印出来,作为刚接触Python的菜鸟,迷瞪了半…

windows mobile做一个摄象头预览程序
zdirectshow的原理大概大家都知道,基本就是用微软封装的接口来实现硬件无关性,但是最终调用的接口都要在驱动层有对应的实现: 为了更清楚地演示directshow的数据传输过程,我必须说明的这个程序的基本流程。我采用的是vs2005 windows mobile 6。0 professional 仿真模拟器&…

初学者的机器学习入门实战教程!
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」,购票请扫码咨询 ↑↑↑作者 | Adrian Rosebrock译者 | kbsc13,京东算法工程师,研究领域计算机视觉来源 | 机器学习与计算机视觉(ID:AI_Developer)这是…

【Qt】调用Python函数:无参数、单个参数、多个参数、数组参数
一、链接配置 如果缺少头文件需要安装python3-dev: sudo apt-get install python3-dev链接libpython3.4库,添加头文件路径,以Qt为例: INCLUDEPATH += /usr/include/python3.4 LIBS += -L /usr/lib/python3.4/config-3.4m-x86_64-linux-gnu -lpython3.4二、头文件 因为p…

分布式系统的问题
本文内容翻译自《Designing Data-Intensive Applications》一书的第8章。 近几章主要介绍系统如何处理错误。例如,我们讨论了副本故障转移,复制滞后和事务的并发控制。当我们理解实际系统中可能出现的各种边界情况时,我们就能更好地处理它们。…

php-cgi占用cpu资源过高的解决方法
转的网上的,不过对PHP-CGI菜鸟的人,还是有点帮助的。 1. 一些php的扩展与php版本兼容存在问题,实践证明 eAccelerater与某些php版本兼容存在问题,具体表现时启动php-cgi进程后,运行10多分钟,奇慢无比&#…

请收下这份NLP热门词汇解读
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」,购票请扫码咨询 ↑↑↑本文转载自微软研究院AI头条(ID:MSRAsia)编者按:在过去的一段时间,自然语言处理领域取得了许多重要的进展,Transformer、BERT、…

【Ubuntu】dpkg: 处理软件包 XXXX (--configure)时出错解决方法
1、使用apt-get --purge remove删除安装包时报错 dpkg: 处理软件包 python-gflags (–configure)时出错: 子进程 已安装 post-installation 脚本 返回了错误号 1 正在设置 python-sklearn (0.14.1-2) … Traceback (most recent call last): File “/usr/bin/pycom…
c#devexpress GridContorl添加进度条
demo 的实现图 下边是步骤和代码 1定义 时钟事件,定时的增加进度条的增量. 2: 添加进度条 3;定义字段属性 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; …

信达充值旗舰店
在淘宝上新开了一个话费 游戏点卡充值的小店,以后大家话费没了可以联系我啊,速度还是蛮快的,都是赔本卖的只想提高点信誉,所以价格也是最最低的了,感谢大家的支持,多多帮忙啊^_^ http://sjzxinda.taobao.co…

完整代码+实操!手把手教你操作Faster R-CNN和Mask R-CNN
点击上方↑↑↑蓝字关注我们~「2019 Python开发者日」全日程揭晓,请扫码咨询 ↑↑↑机器视觉领域的核心问题之一就是目标检测(Object Detection),它的任务是找出图像当中所有感兴趣的目标(物体),…

【Dlib】使用dlib_face_recognition_resnet_model_v1.dat无法实现微调fune-tuning
1、问题描述 dlib官方使用resnet训练人脸识别,训练了300万的数据,网络参数保存在dlib_face_recognition_resnet_model_v1.dat中。 测试中识别lfw数据时,准确率能达到99.13%,但是在识别自己的数据时,准确率有点低&…
Visual Studio 2017 - Windows应用程序打包成exe文件(1)- 工具简单总结
最近有对一个Windows应用程序少许维护和修改。修改之后要发布新的exe安装文件,打包exe文件时,遇到了很头疼的问题,还好最后解决了,记录一下。 Visual Studio版本:Visual Studio 2017 Visual Studio 2017 打包插件 新建…

NET也有闭包
NET也有闭包在.NET中,函数并不是第一级成员,所以并不能像JavaScript那样通过在函数中内嵌子函数的方式实现闭包,通常而言,形成闭包有一些值得总结的非必要条件: 嵌套定义的函数。 匿名函数。 将函数作为参数或…
