当前位置：首页 > 编程日记 > 正文

LTE PUCCH F2 TX/RX汇总

编程日记 2024-03-12 15:00:01

TX

TX端的公式如下(下图来自sharetechnote)：

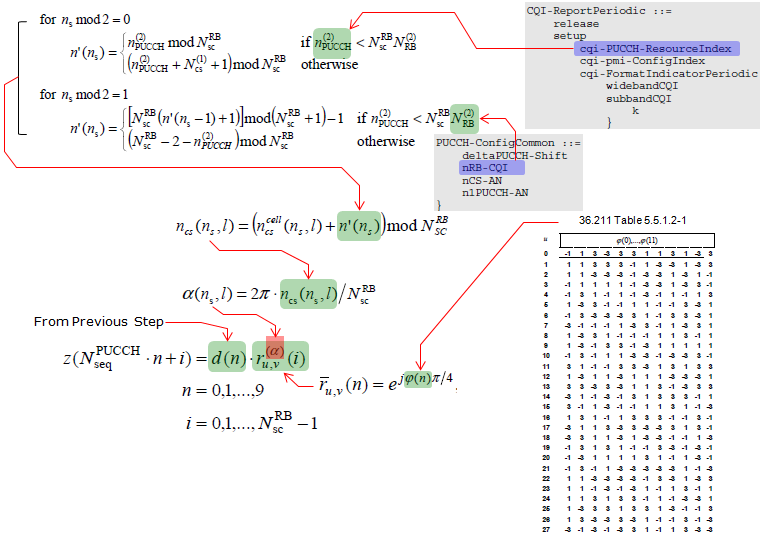
发送端在36.212/36.211中有详细的描述，就是一系列的数学运算，过程概括如下：

编码、加扰、调制的过程暂不介绍，主要介绍下上图中乘以r_uv的过程，公式如下：

$z() = d(n).r^{\alpha}_{u,v}(i)$

$d(n)$ : 是调制后的复数，n=0,1...9

下面介绍 $r^{\alpha}_{u,v}(i)$ ，参考36.211-5.5.1中r_uv的定义：

$r^{\alpha,\delta }_{u,v}(n)=e^{j\alpha(n+\delta\frac{\varpi mod2}{2})}\overline{r}_{u,v}(n)$ $0\leq n< M^{RS}_{sc}$

F2中 $\delta$ =0, 所以上式简化为：

$r^{\alpha}_{u,v}(n)=e^{j\alpha n}\overline{r}_{u,v}(n)$

右边有2部分组成： $e^{j\alpha n}$ 和 $\overline{r}_{u,v}(n)$

1). $e^{j\alpha n}$ ：变化在于 $\alpha$

F2的 $\alpha$ ，参考36.211 - 5.4.2

$\alpha_{\widetilde{p}}(n_{s},l) = 2\pi.n^{(\widetilde{p})}_{cs}(n_s.l)/N^{RB}_{sc}$ , $N^{RB}_{sc}=12$

假设： $X=n^{(\widetilde{p})}_{cs}(n_s.l)$

简化： $\alpha= (2\pi/12)X$ , 即： $e^{j\alpha n} = e^{j(2\pi/12) Xn}$ , 相当于将圆分了N等份。

2). $\overline{r}_{u,v}(n)$ : 基序列(base sequence), 可以参考5.5.1.x, 这里我们假如 $M^{RS}_{sc}=N^{RB}_{sc}$ , 则基序列参考5.5.1.2,

$\overline{r}_{u,v}(n) = e^{j\varphi (n)\pi/4}$ , $0\leq n\leq M^{RS}_{sc}-1$

可见基序列的变化在于 $\varphi (n)$ , 参考36.211中的Table 5.5.1.2-1

$\varphi (n)$ 取决于u值，u:sequence-group number, 参考36.211 - 5.5.1.3

这里我们去u值为0，则 $\varphi (n)$ 的12个值分别为：

n	0	1	2	3	4	5	6	7	8	9	10	11
$\varphi (n)$	-1	1	3	-3	3	3	1	1	3	1	-3	3
$\overline{r}_{u,v}(n)$	$e^{j-\pi/4}$	$e^{j\pi/4}$	$e^{j3\pi/4}$	$e^{j-3\pi/4}$

可以看到相当于将圆分了4等份。

RE mapping:

RX

信道估计(CE)，计算H:

DMRS 12个RE(1symbol *12sc), 每个RE除以r_uv, 然后12个RE求和得到H。

均衡：

Data12个RE(1symbol *12sc), 每个RE除以r_uv, 然后再除以H,得到一个complex, 2个slot 有10 symbol 传输data, 所以可以得到10个complex, 由于采用QPSK调制(实部和虚部各代表一个bit)，10个complex 转化为20个bit, 20个bit 输入译码器可以得到原始的传输数据。

另外，复数相除，乘以复共轭，

$\frac{a}{b} = \frac{a.\overline{b}}{b.\overline{b}} = \frac{a.\overline{b}}{\left | b \right | ^{2}}$

RX端先除以r_uv, 注意 $r^{\alpha}_{u,v}(n)=e^{j\alpha n}\overline{r}_{u,v}(n) =e^{j\alpha n} e^{j\varphi (n)\pi/4} = e^{j(\alpha n+\varphi (n)\pi/4)}$ , 所以r_uv的模方=1.

接着除以了H, H的的模方不等于1，所以分子共轭乘后，别忘了除以分母的模方.

https://www.dkcj.cn/info/3049.html

LTE PUCCH F2 TX/RX汇总

TX

RX

相关文章：

面试题：查询连续出现的数字

php的数组排序方法,PHP数组排序函数

介绍并扩展Fitnesse的测试模块化机制：Scenario

cmake, This may result in binaries being created in the wrong place

GDB调试技巧

php 进程管理,php如何管理进程

Linux分区的认识

求小数的小数点的第n位是什么

Git 简介1-常用术语

要过一遍的博客列表

b站弹幕 xml php 乱码,B站弹幕Python爬行XML响应中的代码转换问题,python,之,取,b,xml,时,转码...

java.io包和杯子测楼

JUnit测试类完成后事务是默认回滚的。只能查询数据，不能增删改。

gcc 编译选项

ionic中的后退方法

php 生成非对称密钥,php实现非对称加密

HDU 4951 Multiplication table(2014 Multi-University Training Contest 8)

H3C 静态默认路由配置

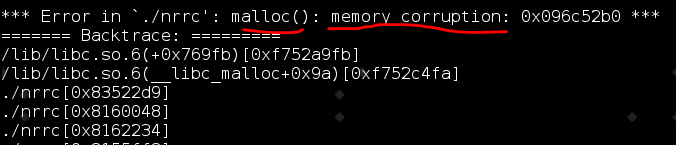
malloc为什么会报错：memory corruption

php 静态类内存,php面向对象中static静态属性与方法的内存位置分析

Android中实现为TextView添加多个可点击的文本

Set和存储顺序深入探讨、SortedSet排序的示例

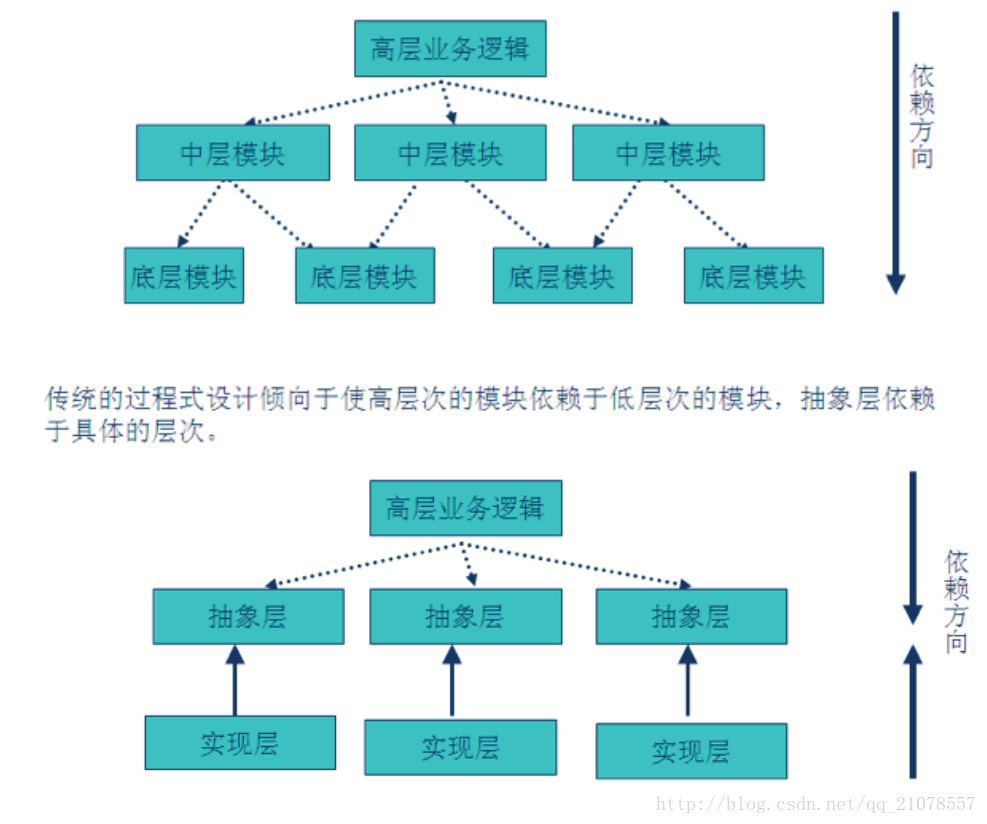
设计模式七大原则(C++描述)

gdb高级调试技巧

php代码实现关键词搜索,PHP代码实现百度统计关键词及来路推送

linux跨主机复制文件

delphi使用outputdebugstring调试程序和写系统日志

一个下载Windows镜像的地址

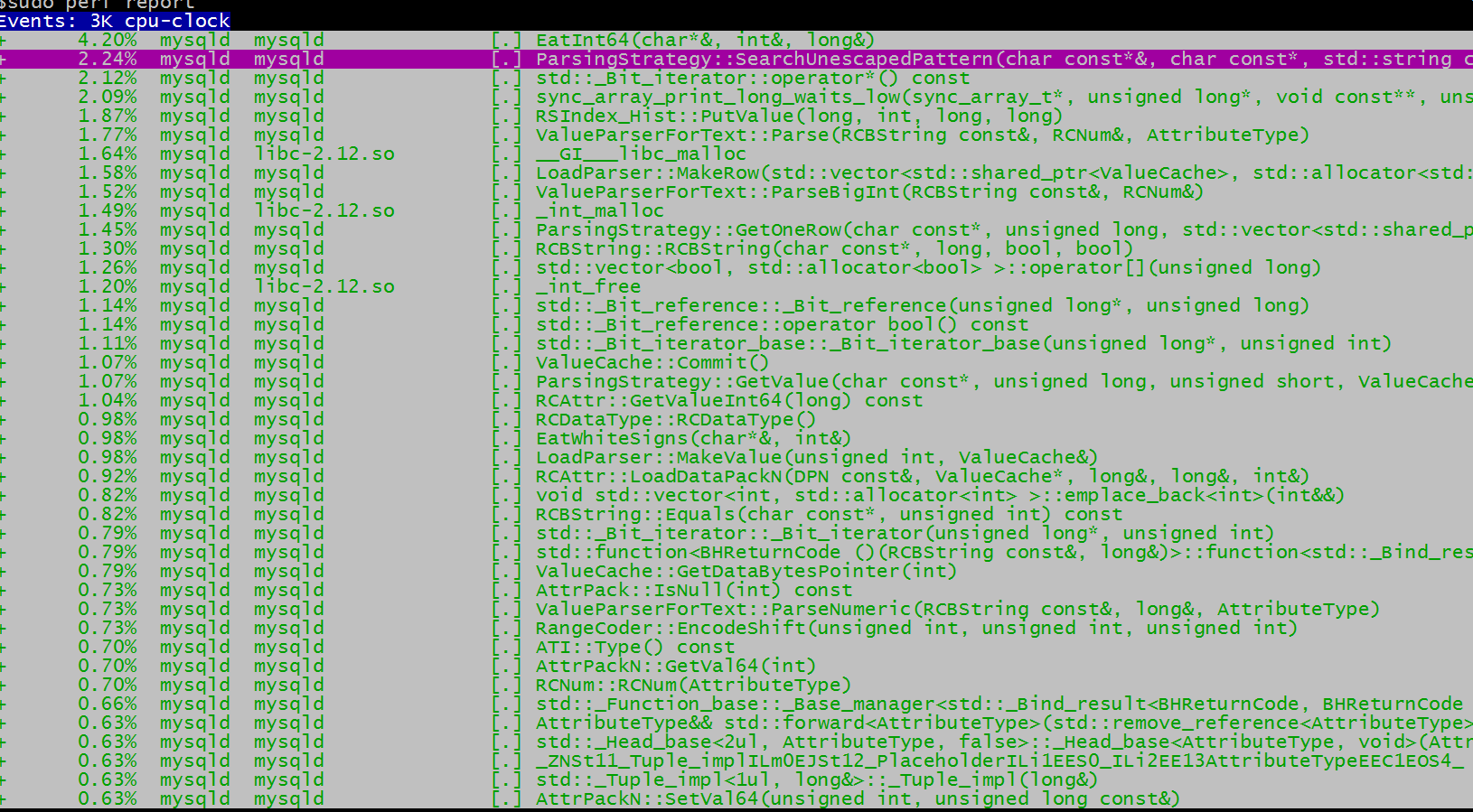
perf + 火焰图分析程序性能

jquery 设置css样式