当前位置：首页 > 编程日记 > 正文

机器学习模型的超参数优化 | 原力计划

编程日记 2024-11-30 01:30:00

作者 | deephub

责编 | 王晓曼

出品 | CSDN博客

头图 | CSDN付费下载自东方IC

引言

模型优化是机器学习算法实现中最困难的挑战之一。机器学习和深度学习理论的所有分支都致力于模型的优化。

机器学习中的超参数优化旨在寻找使得机器学习算法在验证数据集上表现性能最佳的超参数。超参数与一般模型参数不同，超参数是在训练前提前设置的。举例来说，随机森林算法中树的数量就是一个超参数，而神经网络中的权值则不是超参数。

其它超参数有：

神经网络训练中的学习率
支持向量机中的 c cc 参数和 γ \gammaγ 参数
k 近邻算法中的 k kk 参数
……

超参数优化找到一组超参数，这些超参数返回一个优化模型，该模型减少了预定义的损失函数，进而提高了给定独立数据的预测或者分类精度。

分类算法中的超参数

超参数优化方法

超参数的设置对于模型性能有着直接影响，其重要性不言而喻。为了最大化模型性能，了解如何优化超参数至关重要。接下来介绍了几种常用的超参数优化方法。

1.手动调参

很多情况下，工程师们依靠试错法手动对超参数进行调参优化，有经验的工程师能够很大程度上判断超参数如何进行设置能够获得更高的模型准确性。但是，这一方法依赖大量的经验，并且比较耗时，因此发展出了许多自动化超参数优化方法。

2. 网格化寻优（Grid Search）

网格化寻优可以说是最基本的超参数优化方法。使用这种技术，我们只需为所有超参数的可能构建独立的模型，评估每个模型的性能，并选择产生最佳结果的模型和超参数。

网格化寻优方法：

以一个典型的核函数为 RBF 的 SVM 分类模型为例，其至少有两个超参数需要优化——正则化常数 c cc 和核函数参数 γ \gammaγ。

这两个超参数都是连续的，需要执行网格化寻优为每个超参数选择合理取值。假设 c∈10,100,1000,γ∈0.1,0.2,0.5,1.0c\in {10,100,1000}, \gamma \in {0.1,0.2,0.5,1.0}c∈10,100,1000,γ∈0.1,0.2,0.5,1.0。

那么网格化寻优方法将对每一对( c cc ,γ \gammaγ)赋值后的 SVM 模型进行训练，并在验证集上分别评估它们的性能（或者在训练集内进行 cross-validation）。

最终，网格化寻优方法返回在评估过程中得分最高的模型及其超参数。

通过以下代码，可以实现上述方法：

首先，通过 sklearn 库调用 GridSearchCV 。

from sklearn.datasets import load_iris
from sklearn.svm import SVC
iris = load_iris()
svc = SVR()
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
grid = GridSearchCV(estimator=SVR(kernel='rbf'),param_grid={'C': [0.1, 1, 100, 1000],'epsilon': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 5, 10],'gamma': [0.0001, 0.001, 0.005, 0.1, 1, 3, 5]},cv=5, scoring='neg_mean_squared_error', verbose=0, n_jobs=-1)

然后拟合网格:

grid.fit(X,y)

输出结果:

#print the best score throughout the grid search
print grid.best_score_
#print the best parameter used for the highest score of the model.
print grid.best_param_

网格化寻优的一个缺点是，当涉及到多个超参数时，计算数量呈指数增长。并且这一方法并不能保证搜索会找到完美的超参数值。

随机寻优（Random Search）

通常并不是所有的超参数都有同样的重要性，某些超参数可能作用更显著。

而随机寻优方法相对于网格化寻优方法能够更准确地确定某些重要的超参数的最佳值。

随机寻优方法：

随机寻优方法在超参数网格的基础上选择随机的组合来进行模型训练。

可以控制组合的数量，基于时间和计算资源的情况，选择合理的计算次数。

这一方法可以通过调用 sklearn 库中的 RandomizedSearchCV 函数来实现。

尽管 RandomizedSearchCV 的结果可能不如 GridSearchCV 准确，但它令人意外地经常选择出最好的结果，而且只花费 GridSearchCV 所需时间的一小部分。

给定相同的资源，RandomizedSearchCV 甚至可以优于的结果可能不如GridSearchCV准确。当使用连续参数时，两者的差别如下图所示。

网格化寻优 VS 随机寻优

随机寻优方法找到最优参数的机会相对更高，但是这一方法适用于低维数据的情况，可以在较少迭代次数的情况下找到正确的参数集合，并且花费的时间较少。

通过以下代码，可以实现上述方法：

首先，通过 sklearn 库调用 RandomizedSearchCV 。

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestRegressor
iris = load_iris()
rf = RandomForestRegressor(random_state = 42)
from sklearn.model_selection import RandomizedSearchCV
random_grid = {'n_estimators': n_estimators,'max_features': max_features,'max_depth': max_depth,'min_samples_split': min_samples_split,'min_samples_leaf': min_samples_leaf,'bootstrap': bootstrap}
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1)# Fit the random search model

然后进行计算：

rf_random.fit(X,y)

输出结果：

#print the best score throughout the grid search
print rf_random.best_score_
#print the best parameter used for the highest score of the model.
print rf_random.best_param_Output:
{'bootstrap': True,'max_depth': 70,'max_features': 'auto','min_samples_leaf': 4,'min_samples_split': 10,'n_estimators': 400}

贝叶斯优化方法（Bayesian Optimization）

前面两种方法能够针对单独超参数组合模型进行训练，并评估各自的性能。每个模型都是独立的，因此很易于进行并行计算。

但是每个模型都是独立的，也导致模型之间不具有指导意义，前一模型的计算结果并不能影响后一模型的超参数选择。

而贝叶斯优化方法（顺序优化方法的一种，sequential model-besed optimization, SMBO）则可以借鉴已有的结果进而影响后续的模型超参数选择。

这也限制了模型训练评估的计算次数，因为只有有望提高模型性能的超参数组合才会被进行计算。

贝叶斯优化是通过构造一个函数的后验分布（高斯过程）来工作的，该后验分布最好地描述了要优化的函数。

随着观测次数的增加，后验分布得到改善，算法更加确定参数空间中哪些区域值得探索，哪些区域不值得探索。

当反复迭代时，算法会在考虑到它对目标函数的了解的情况下，平衡它的探索和开发需求。

在每个步骤中，高斯过程被拟合到已知的样本（先前探索的点），后验分布与探索策略（例如UCB（上置信限，upper confidence bound）或EI（预期改善, expected improvement））被用于确定下一个应该探索的点。

通过贝叶斯优化方法，可以更高效的探索超参数变量空间，降低优化时间。

基于梯度的优化方法（Gradient-based Optimization）

基于梯度的优化方法经常被用于神经网络模型中，主要计算超参数的梯度，并且通过梯度下降算法进行优化。

这一方法的应用场景并不广泛，其局限性主要在于：

超参数优化通常不是一个平滑的过程
超参数优化往往具有非凸的性质

进化寻优（Evolutionary Optimization）

进化寻优方法的思想来源于生物学概念，由于自然进化是不断变化的环境中发生的一个动态过程，因此适用于超参数寻优问题，因为超参数寻优也是一个动态过程。

进化算法经常被用来寻找其他技术不易求解的近似解。优化问题往往没有一个精确的解决方案，因为它可能太耗时并且计算资源占用很大。

在这种情况下，进化算法通常可以用来寻找一个足够的近似最优解。

进化算法的一个优点是，它们可以产生出不受人类误解或偏见影响的解决方案。

作为一个一般性的经验法则，任何时候想要优化调整超参数，优先考虑网格化寻优方法和随机寻优方法！

总结

在本文中，我们了解到为超参数找到正确的值可能是一项令人沮丧的任务，并可能导致机器学习模型的欠拟合或过拟合。我们看到了如何通过使用网格化寻优、随机寻优和其他算法来克服这一障碍。

原文链接：https://blog.csdn.net/m0_46510245/article/details/105910907

6月2日20:00，CSDN 创始人&董事长、极客帮创投创始合伙人蒋涛携手全球顶级开源基金会主席、董事，聚焦中国开源现状，直面开发者在开源技术、商业上的难题，你绝不可错过的开源巅峰对谈！立即免费围观：

推荐阅读

追忆童年，教你用Python画出儿时卡通人物
如何用NLP辅助投资分析？三大海外机构落地案例详解
What?! Python一行代码，能玩这么多童年的游戏？
我只是追个直播，结果被拉进大咖们的群面对面群聊……
借助大数据进行社交媒体营销，企业们得这么玩！
力挺比特币的世界第2交易员：仅次于索罗斯，连续25年无亏损

你点的每个“在看”，我都认真当成了喜欢

https://www.dkcj.cn/info/29707.html

机器学习模型的超参数优化 | 原力计划

相关文章：

准备IE--复习NP，NP从头开始，每天学一点，就多一点收获

[20160608]自治事务引起死锁.txt

动感效果的TAB选项卡 jquery 插件

Linux上隐藏进程名（初级版)

神操作！一行Python代码搞定一款游戏？给力！

jquery对所有input type=text的控件赋值

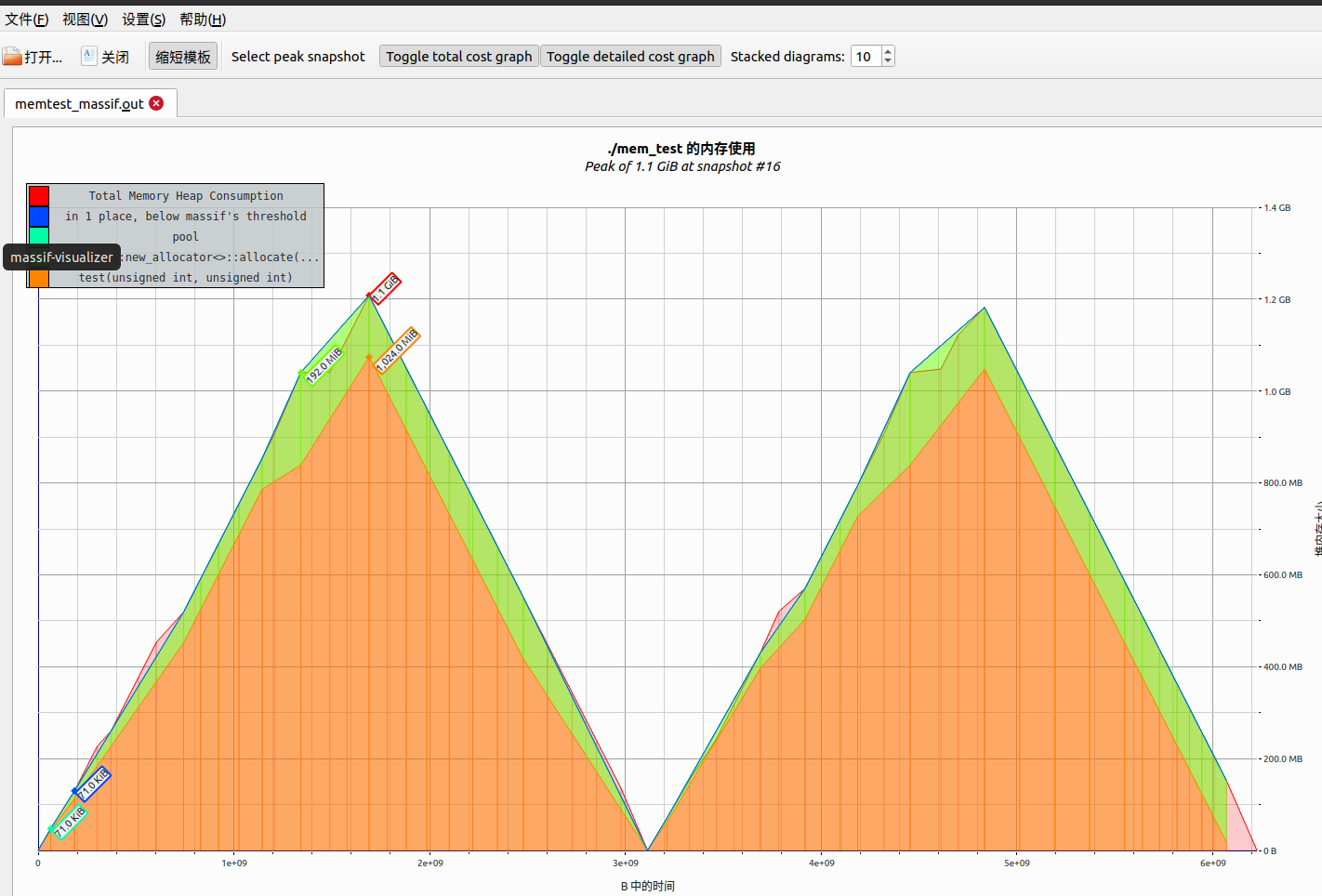
free not return memory

成大事必备9种能力

懂语言者得天下：NLP凭什么被称为人工智能的掌上明珠？

[转]SIFT特征提取分析

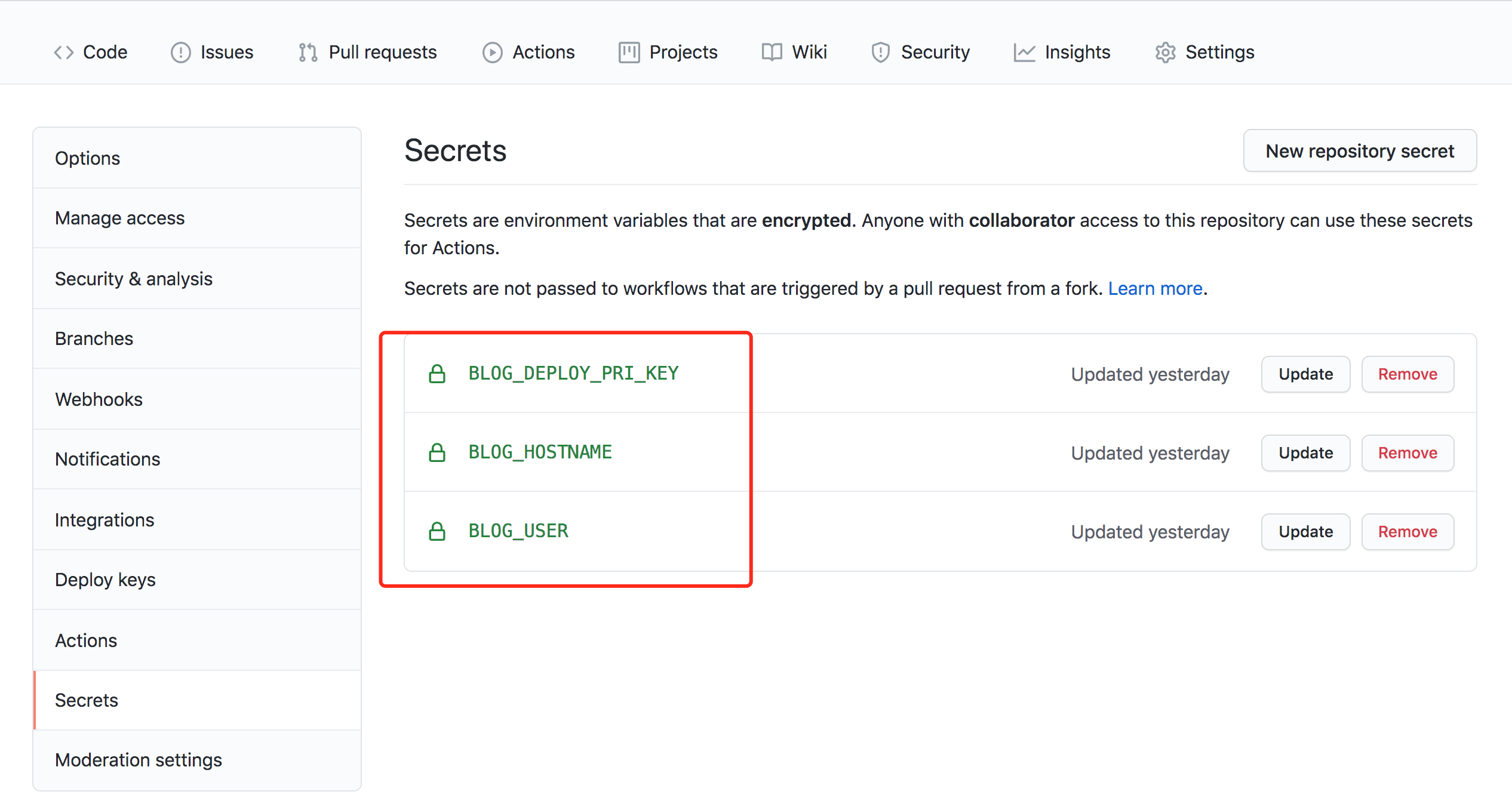
博客大事记之迁移博客到香港主机

限时福利：腾讯高级专家手把手教你打造 OCR 神器！

C++与.net的编译方式

awk (一)

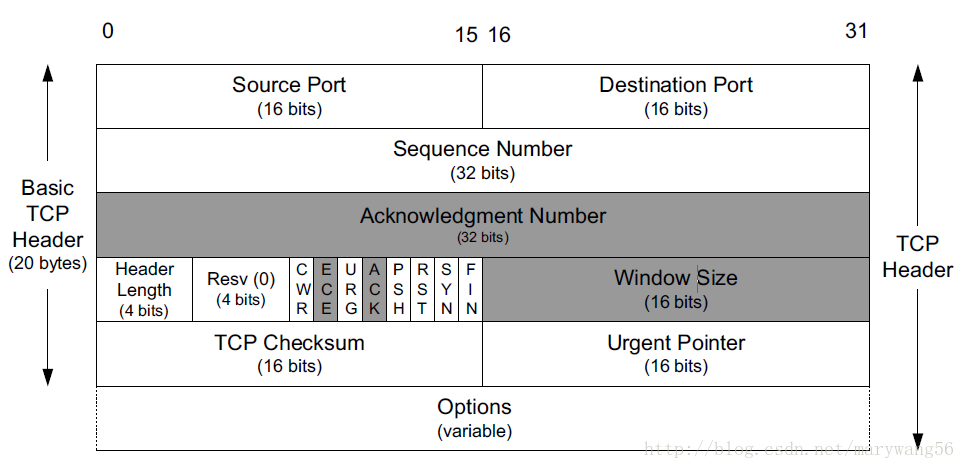
TCP全连接和半连接的问题探讨

[转] ASP.NET MVC3 路由和多数据集的返回

给Python代码加上酷炫进度条的几种姿势

(转)mongodb分片

深入浅出paxos

Uber 前无人驾驶工程师告诉你，国内无人驾驶之路还要走多久？

oracle服务

B00009 C语言分割字符串库函数strtok

WEB打印大全

漫画 | 程序媛小姐姐带你一次了解什么是排序算法

POJ 1207 The 3n + 1 problem

PopupWindow响应返回键的问题

Unix / Linux世界里的4-2-1

深度学习概述：NLP vs CNN

oracle 求A中不存在于B的记录

正则表达式grep、egrep--already