二叉堆的定义
二叉堆是全然二叉树或者是近似全然二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)不论什么一个子节点的键值。
2.每一个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于不论什么一个子节点的键值时为最大堆。当父结点的键值总是小于或等于不论什么一个子节点的键值时为最小堆。下图展示一个最小堆:
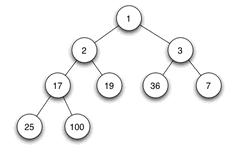
因为其他几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除
以下先给出《数据结构C++语言描写叙述》中最小堆的建立插入删除的图解,再给出本人的实现代码,最好是先看明确图后再去看代码。
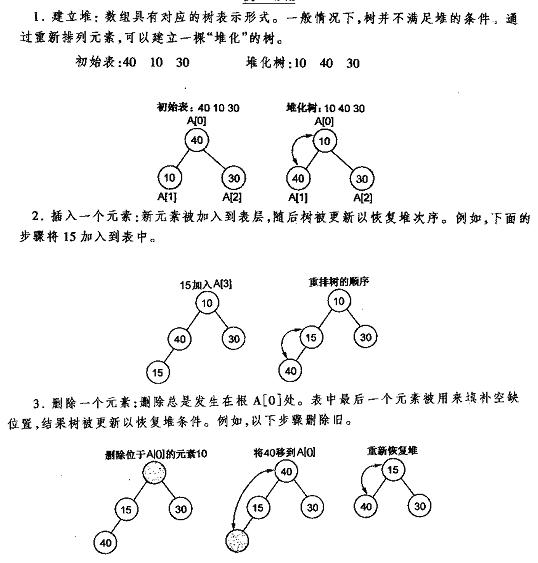
堆的插入
每次插入都是将新数据放在数组最后。能够发现从这个新数据的父结点到根结点必定为一个有序的数列,如今的任务是将这个新数据插入到这个有序数据中——这就相似于直接插入排序中将一个数据并入到有序区间中,对比《白话经典算法系列之二 直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码:
// 新添�i结点 其父结点为(i - 1) / 2
void MinHeapFixup(int a[], int i)
{int j, temp;temp = a[i];j = (i - 1) / 2; //父结点while (j >= 0 && i != 0){if (a[j] <= temp)break;a[i] = a[j]; //把较大的子结点往下移动,替换它的子结点i = j;j = (i - 1) / 2;}a[i] = temp;
}更简短的表达为:
void MinHeapFixup(int a[], int i)
{for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)Swap(a[i], a[j]);
}插入时:
//在最小堆中添�新的数据nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{a[n] = nNum;MinHeapFixup(a, n);
}堆的删除
按定义,堆中每次都仅仅能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点開始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,假设父结点比这个最小的子结点还小说明不须要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。以下给出代码:
// 从i节点開始调整,n为节点总数 从0開始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{int j, temp;temp = a[i];j = 2 * i + 1;while (j < n){if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的j++;if (a[j] >= temp)break;a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点i = j;j = 2 * i + 1;}a[i] = temp;
}
//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{Swap(a[0], a[n - 1]);MinHeapFixdown(a, 0, n - 1);
}堆化数组
有了堆的插入和删除后,再考虑下怎样对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,例如以下图:
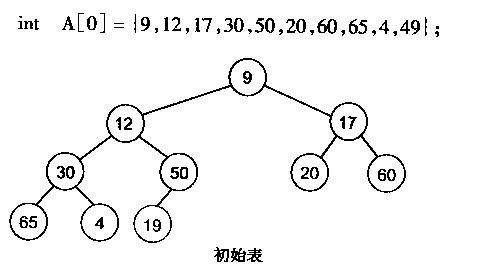
非常明显,对叶子结点来说,能够觉得它已经是一个合法的堆了即20,60, 65, 4, 49都各自是一个合法的堆。仅仅要从A[4]=50開始向下调整就能够了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就能够了。下图展示了这些步骤:
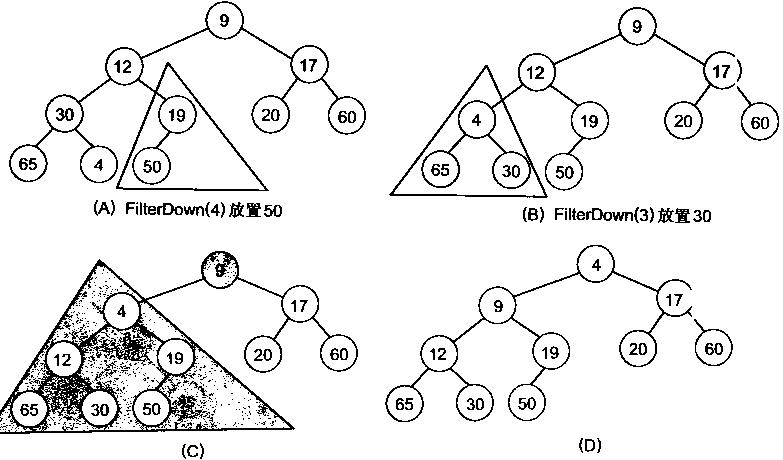
写出堆化数组的代码:
//建立最小堆
void MakeMinHeap(int a[], int n)
{for (int i = n / 2 - 1; i >= 0; i--)MinHeapFixdown(a, i, n);
}
至此,堆的操作就所有完毕了(注1),再来看下怎样用堆这种数据结构来进行排序。
堆排序
首先能够看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再运行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,反复上述步骤直至堆中仅仅有一个数据时就直接取出这个数据。
因为堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]又一次恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]又一次恢复堆,反复这种操作直到A[0]与A[1]交换。因为每次都是将最小的数据并入到后面的有序区间,故操作完毕后整个数组就有序了。有点相似于直接选择排序。
void MinheapsortTodescendarray(int a[], int n)
{for (int i = n - 1; i >= 1; i--){Swap(a[i], a[0]);MinHeapFixdown(a, 0, i);}
}注意使用最小堆排序后是递减数组,要得到递增数组,能够使用最大堆。
因为每次又一次恢复堆的时间复杂度为O(logN),共N - 1次又一次恢复堆操作,再加上前面建立堆时N / 2次向下调整,每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数,能够參阅《STL系列之四 heap 堆》。
注1 作为一个数据结构,最好用类将其数据和方法封装起来,这样即便于操作,也便于理解。此外,除了堆排序要使用堆,另外还有非常多场合能够使用堆来方便和高效的处理数据,以后会一一介绍。
转载请标明出处,原文地址:http://blog.csdn.net/morewindows/article/details/6709644