pcl求平面法向量_线性代数6——平面方程与矩阵
线性方程的几何意义
二元线性方程
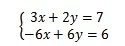
该方程是一个二元线性方程组,包含两个方程,每个方程是一条直线,两条直线的交点就是该方程有唯一解,这就是二元线性方程的几何意义。
平面方程
空间内不在同一直线上的三点构成一个平面,平面方程可表示为
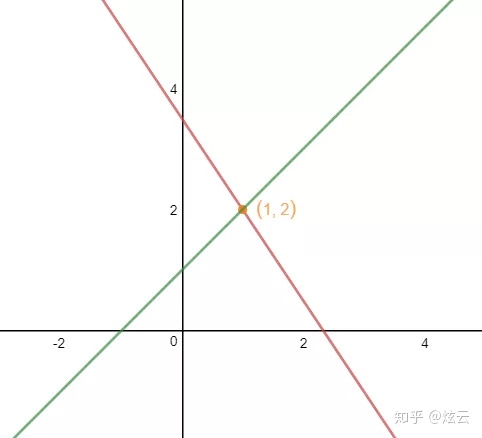
方程x + 4y + z = 8,在xyz三个坐标轴上的截距分别是(8,0,0),(0,2,0),(0,0,8),下图是该函数在坐标轴上的示意图:
需要注意的是,平面是无限延伸的。
根据法向量求平面方程
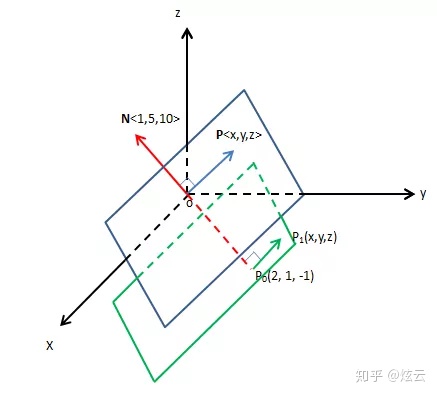
现在需要找到一个过原点的平面,它有一个过原点的法向量是
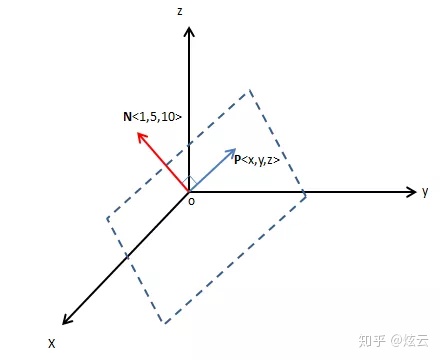
如上图所示,P<x, y, z>是所求平面上的向量,法向量N⊥OP,因此:
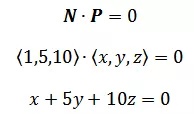
这就是平面方程。
再看一个稍微不同点的问题,一个平面的法向量是N<1, 5, 10>,该平面经过
由于拥有同一个法向量,所以这是与上一个平面平行的平面:
平面上的任意点
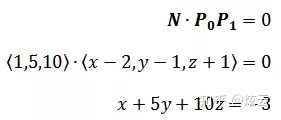
上面两个方程唯一的不同点就是
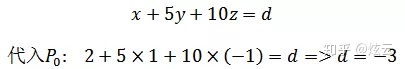
示例
向量V = <1, 2, -1>与平面x + y + 3z = 5的关系?
平面的法向量N = <1, 1, 3>,容易看出,V·N = 1×1 + 2×1 + (-1)×3 = 0,V⊥N,向量V与平面平行。需要注意的是,向量不是点(实际上向量有无数点),<1, 2, -1>不同于(1, 2, -1),在没有特殊说明的情况下,可以认为向量从原点出发。如果向量V从原点出发,V经过点(1, 2, -1),但该点并不在平面上。
平面方程组的解
三元线性方程组
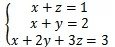
,设三个平面分别是
平面方程组也可能出现无解的情况,一种典型的情况是三个平面平行。如果

无数解和无解
总结一下,如果
- 与
相交于一点,则方程组有唯一解;
- 在
上,则方程组有无数解;
- 与
平行,且不在
上,方程组无解。
当然,如果
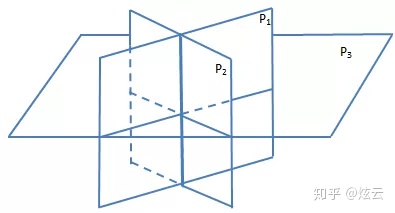
点到平面的距离
平面方程是ax + by + cz = d,平面外一点
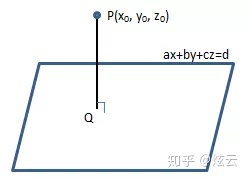
PQ垂直于平面,现在要求PQ的长度,但是并不知道Q点的具体数值。
设
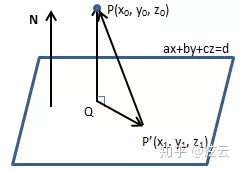
向量QP是P’ P在法向量N方向上的分量,也就是P’ P与N相同方向的单位向量的点积。(可参考《线性代数3——向量2(点积)》)设距离为D,则:

求解线性方程
当然可以使用初中的代数知识求解线性方程组,这里主要讨论如何用矩阵求解。
消元法
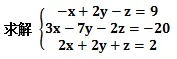
首先将方程组以矩阵的方式表示:
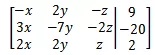
该矩阵称为增广矩阵。由于是线性方程组,可以省略未知数:
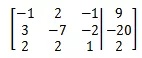
现在可以对其进行消元,首先消去x,方法与普通代数法类似:
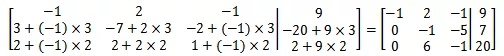
用同样的方法对y消元:
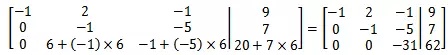
矩阵第三行对应
最终可解得
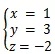
可以看出,消元法本质上与初中的代数法没有区别,只是换了一种较为简单的表现形式,对于多元线性方程组,其消元过程十分繁琐。
矩阵法
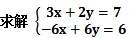
这里需要使用列向量的概念,列向量是一个 n×1 的矩阵,即矩阵由一个含有n个元素的列所组成:列向量的转置是一个行向量,反之亦然。
将上面的方程组用矩阵和向量表示:
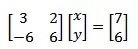

实际上可看作 x = b/A,有点意思了,可以通过一个除法运算直接求得方程的解。
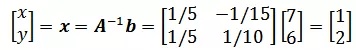
解得
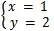
对于多元线性方程组,使用矩阵法求解比消元法简单的多。
我们用python求解消元法中的方程组
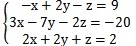
import numpy as np
a = np.matrix([[-1,2,-1],[3,-7,-2],[2,2,1]])
c = np.matrix([[9,-20,2]]).T
result = a**-1 * c
print(result)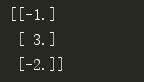
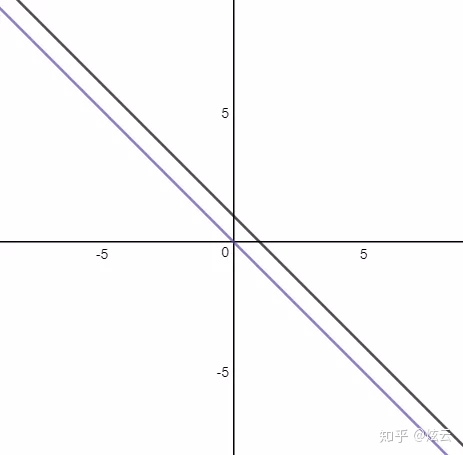
无解的方程组
线性方程组在用矩阵向量法转换后,如果矩阵A是奇异矩阵,
如
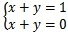
,该方程组无解,
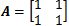
是奇异矩阵。下图是该方程组在坐标轴上的图像:
示例
示例1 求下面的平面方程:
a) 已知平面的法向量N = <1, 2, 3>,平面过点(1, 0, -1)
b) 平面过原点且平行于两个向量A = <1, 0, -1>和B = <-1, 2, 0>
c) 平面过点P1(1, 2, 0), P2(3, 1, 1), P3(2, 0, 0)
d) 平面与a中的平面平行,且经过点(1 , 2, 3) a.
平面方程
将点(1, 0, -1) 代入平面方程,
平面方程是
平面方程ax + by + cz = d
∵A,B过原点,且与平面平行,并且平面过原点
∴A,B在平面上,d = 0
已知平面上两个个向量从同一点出发的向量,计算平面的法向量:
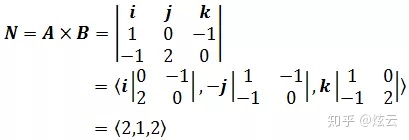
平面方程是 2x + y + 2z = 0
根据叉积计算法向量可参考《线性代数4——向量3(叉积)》 c.
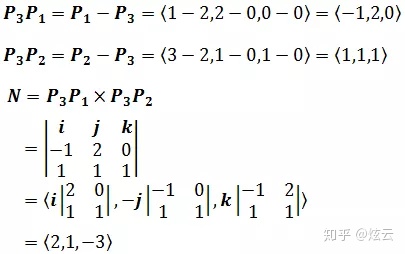
平面方程2x + y – 3z = d,取任意点代入,d = 4。平面方程是2x + y – 3z = 4 d.
a的平面是x + 2y + 3z = -2,由于该平面平行于a,所以该平面是x + 2y + 3z = d。
将点(1 , 2, 3)代入,1 + 2×2 + 3×3 = 14 = d
平面方程是x + 2y + 3z = 14
示例2
求原点到平面2x + y -2z = 4的距离。
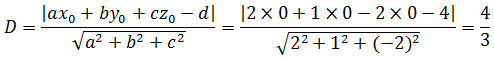
总结
- 二元线性方程组的几何意义是平面上的两条直线,其解是二者的交点
- 三元线性方程组的几何意义是三维空间上的三个平面,可能存在唯一解、无数解或无解
- 平面方程用ax + by + cz = d,点到平面的距离
4.如果线性方程组对应的矩阵是奇异矩阵,则该方程组无解
相关文章:

php 类中的各种拦截器
1、__get( $property ) 访问未定义的属性时调用class lanjie {function __get($name){echo $name." property not found! ";} }$ob new lanjie(); echo $ob->g; 当我们调用对象$ob未定义的属性g时,调用拦截器__get()方法,输出“g property…

[Vue CLI 3] 源码之 webpack-chain
我们看一下 webpack-chain 到底做什么? Use a chaining API to generate and simplify the modification of Webpack version 2-4 configurations.熟悉 cli-plugin-babel、cli-plugin-eslint 源码的话,你会时常看到它。 如何使用呢? 1、加载它 const Co…

openstack页面自定义插件使用详解(django、ajax、post)(zTree为例)
2019独角兽企业重金招聘Python工程师标准>>> 感谢朋友支持本博客,欢迎共同探讨交流,由于能力和时间有限,错误之处在所难免,欢迎指正! 如有转载,请保留源作者博客信息。 Better Me的博客…

lazyload.js实现图片异步延迟加载
所谓图片异步加载,意思是不用一次把图片全部加载完,你可以叫它延迟加载,缓冲加载都行。 看看你有没有这种需求:某篇文章图片很多,如果在载入文章时就载入所有图片,无疑会延缓载入速度,让用户等…

postfilter中文什么意思_Filterpost请求中文字符编码的过滤器 --学习笔记
java代码:import java.io.IOException;import java.io.PrintWriter;import javax.servlet.ServletException;import javax.servlet.http.HttpServlet;import javax.servlet.http.HttpServletRequest;import javax.servlet.http.HttpServletResponse;public class Lo…

错误:You can't specify target table 'xxx' for update in FROM clause的解决
今天在MySQL数据库删除重复数据的时候遇到了一个问题。如下脚本: DELETE FROM tempA WHERE tid IN ( SELECT MAX(tid) AS tid FROM tempA GROUP BY name,age ) 会出现报错信息: You cant specify target table tempA for update in FROM clause 大致意思…

HTTPS的七个神话(译文)
原文网址:http://blog.httpwatch.com/2011/01/28/top-7-myths-about-https/ 译文地址:http://www.ruanyifeng.com/blog/2011/02/seven_myths_about_https.html 误解七:HTTPS无法缓存 许多人以为,出于安全考虑,浏览器不…

蓝牙写入数据库_蓝牙 数据写入 简单易懂版(适合没写过蓝牙的看)
//字符串转arrbufferfunction string2buffer(str) {// 首先将字符串转为16进制let val ""for (let i 0; i < str.length; i) {if (val ) {val str.charCodeAt(i).toString(16)} else {val , str.charCodeAt(i).toString(16)}}// 将16进制转化为ArrayBufferr…

Educational Codeforces Round 9 F. Magic Matrix 最小生成树
F. Magic Matrix题目连接: http://www.codeforces.com/contest/632/problem/F Description Youre given a matrix A of size n n. Lets call the matrix with nonnegative elements magic if it is symmetric (so aij aji), aii 0 and aij ≤ max(aik, …

【SqlServer】SqlServer中的更新锁(UPDLOCK)
UPDLOCK.UPDLOCK 的优点是允许您读取数据(不阻塞其它事务)并在以后更新数据,同时确保自从上次读取数据后数据没有被更改。当我们用UPDLOCK来读取记录时可以对取到的记录加上更新锁,从而加上锁的记录在其它的线程中是不能更改的只能…

Oracle CDC (Change Data Capture)更新数据捕获——概述
Change Data Capture能高效识别并捕获数据的插入、修改和删除,使更新数据供个人或应用使用。 CDC从oracle 9i开始引入,//TODO 在11G R2之后的版本里将取消支持,被Oracle GoldenGate取代。 CDC的一些概念 CDC有同步和异步两种模式,…

flutter ios启动白屏_Flutter技术架构概览
前言最近在整理各种技术架构,给自己的列了个TODO list,希望能在几个月的时间内,研究完各种前端技术架构,包括移动端技术架构。今天分享一下自己整理的flutter技术架构。完整的技术架构TODO list可以去我的github仓库查看ÿ…

SQL Relay开源的数据库池连接代理服务器
一、SQL Relay是什么? SQL Relay是一个开源的数据库池连接代理服务器 二、SQL Relay支持哪些数据库?* Oracle* MySQL* mSQL* PostgreSQL* Sybase* MS SQL Server* IBM DB2* Interbase* Sybase* SQLite* Lago* ODBC* MS Access三、安装和配置;…

关于Android开源库分享平台,(GitClub)微信小程序的开发体验
七八月份的深圳一直在下雨,总有人说雨天适合窝在家看书,对于程序开发者来说更是难得的学习机会。我们502工作室的小伙伴利用这个时间学习了一下微信小程序开发,并上线了一个GitClub小程序,目前功能有些简陋,难免有辣眼…

RSync实现文件备份同步
rsync是类unix系统下的数据镜像备份工具,从软件的命名上就可以看出来了——remote sync。它的特性如下:1、可以镜像保存整个目录树和文件系统。2、可以很容易做到保持原来文件的权限、时间、软硬链接等等。3、无须特殊权限即可安装。4、优化的流程&#…
Hibernate annotation多对多配置
角色(用户组),用户多对多。 角色实体配置: private Set<TAuthUser> users;ManyToManyJoinTable(name"t_auth_user_role",joinColumns{JoinColumn(name"role_id")},inverseJoinColumns{JoinColumn(name&…
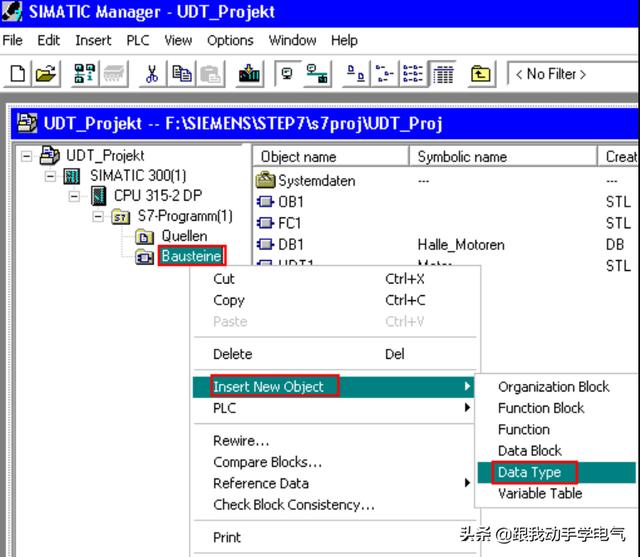
ajax中的url如何传递变量_如何创建和参数化UDT数据类型中的变量及IN,OUT 等参数?...
从数据类型的意义上说 UDT 并不被 CPU 所识别,而是在离线程序中自定义(组合)的数据类型。 S7 程序的自定义数据类型并不能装载到 S7 CPU 中。UDT 是由递增的编辑器创建并编辑或由源文件的编译而生成。 当在块调用中进行变量传递时是不能将 UDT 作为内存地址区域来传…

[雪峰磁针石博客]kotlin书籍汇总
2019独角兽企业重金招聘Python工程师标准>>> 下载地址 Learning Kotlin by Building Android Applications - 2018 初级 Develop amazing applications that will help you understand and explore the fundamentals of Kotlin while covering 3 various types of p…

web集群时session同步的3种方法
web集群时session同步的3种方法在做了web集群后,你肯定会首先考虑session同步问题,因为通过负载均衡后,同一个IP访问同一个页面会被分配到不同的服务器上,如果session不同步的话,一个登录用户,一会是登录状…

属于python文件的操作有_Python的文件操作
1、初始文件操作1、使用python读写文件使用open()函数获取文件句柄,就可以操作文件了,根据打开方式不同能执行的操作也不同。打开方式有:r、w、a、r、w、a、rb、wb、ab、rb、wb、ab,默认用的是r模式2、只读操作(r、rb)2.1、只读模…

[iOS]开发者证书和描述文件的作用
先说下证书吧。 然后是描述文件 转载于:https://www.cnblogs.com/wangqi1221/p/5240273.html

单元格编辑后级联汇总刷新
单元格编辑 级联刷新 PDERPDB db new PDERPDB(); int conid 0; int pid 0; string sql ""; string sqlC ""; if (int.TryParse(Pid, out pid)) { sql string.Format(" UPDATE JL_Project set PCMoney{0} where Pid{1};", pcmoney, Pid); }…

HTTP 协议的通用头域via 的意义以及作用
列出从客户端到 OCS 或者相反方向的响应经过了哪些代理服务器,他们用 什么协议(和版本)发送的请求。 当客户端请求到达第一个代理服务器时,该服务器会在自己发出的请求里面 添…

6-5-树的双亲表示法-树和二叉树-第6章-《数据结构》课本源码-严蔚敏吴伟民版...
课本源码部分 第6章 树和二叉树 - 树的双亲表示法 ——《数据结构》-严蔚敏.吴伟民版 源码使用说明 链接☛☛☛ 《数据结构-C语言版》(严蔚敏,吴伟民版)课本源码习题集解析使用说明 课本源码合辑 链接☛☛☛ 《数据结构》课本源码合辑 习题集全解析 …

压力测试 闪存_产品评测 | HPE Nimble AF全闪存系列,诠释真正的高端存储
随着AI、互联网、大数据等技术快速发展,企业对存储设备的需求已踏上一个更高的级别,高性能、低延时、大容量等多种需求的应用场景愈发常见,在这种情况下,寻求能够满足相应工作负载能力的存储设备已成为企业IT管理者的当务之急。这…

Mysql无法选取非聚合列
教程所示图片使用的是 github 仓库图片,网速过慢的朋友请移步>>> (原文)Mysql 无法选取非聚合列。 更多讨论或者错误提交,也请移步。 1. 前言 最近升级博客,给文章页面底部增加了两个按钮,可以直接…
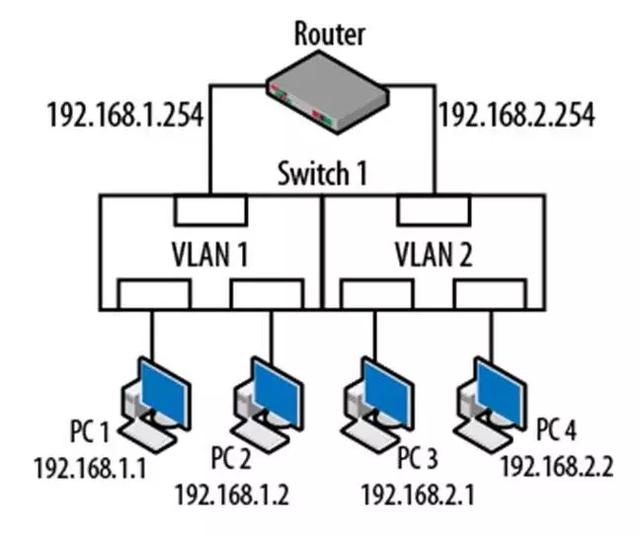
网络设置巨形帧_Trunk的概念与设置
在二层交换机的性能参数中,常常提到一个重要的指标:TRUNK ,许多的二层交换机产品在介绍其性能时,都会提到能够支持TRUNK 功能,从而可以为互连的交换机之间提供更好的传输性能。那到底什么是TRUNK呢?使用TRU…

epoll使用详解
epoll的工作原理是,你如果想进行IO操作时,先向epoll查询是否可读或可写,如果处于可读或可写状态后,epoll会通过epoll_wait函数通知你,此时你再进行进一步的recv或send操作。epoll仅仅是一个异步事件的通知机制…

软件测试(一)
最近的时间内,我印象最深刻的Bug是在上学期的javaweb的大作业中。 其中的要求是在工作人员的每一条记录后面添加一个修改按钮,要求把前一个页面的内容带入到下一个页面中,由于密码采用的是MD5的加密,所以带入到后面的页面中的内容…

网络分流器-网络分流器IP网络路由交换测试技术探讨
网络分流器1 . 与流量相关的L2-3层高级测试技术探讨戎腾网络分流器: 对于一个L2-3层网络设备,最基本、最重要的测试是流量转发性能测试。作为一个网络转发设备,首先要保证可以高速、低时延、稳定地转发流量。相关的性能测试通常是通过流量生成器…
