题目连接:
http://www.codeforces.com/contest/632/problem/F
Description
You're given a matrix A of size n × n.
Let's call the matrix with nonnegative elements magic if it is symmetric (so aij = aji), aii = 0 and aij ≤ max(aik, ajk) for all triples i, j, k. Note that i, j, k do not need to be distinct.
Determine if the matrix is magic.
As the input/output can reach very huge size it is recommended to use fast input/output methods: for example, prefer to use scanf/printf instead of cin/cout in C++, prefer to use BufferedReader/PrintWriter instead of Scanner/System.out in Java.
Input
The first line contains integer n (1 ≤ n ≤ 2500) — the size of the matrix A.
Each of the next n lines contains n integers aij (0 ≤ aij < 109) — the elements of the matrix A.
Note that the given matrix not necessarily is symmetric and can be arbitrary.
Output
Print ''MAGIC" (without quotes) if the given matrix A is magic. Otherwise print ''NOT MAGIC".
Sample Input
3
0 1 2
1 0 2
2 2 0
Sample Output
MAGIC
Hint
题意
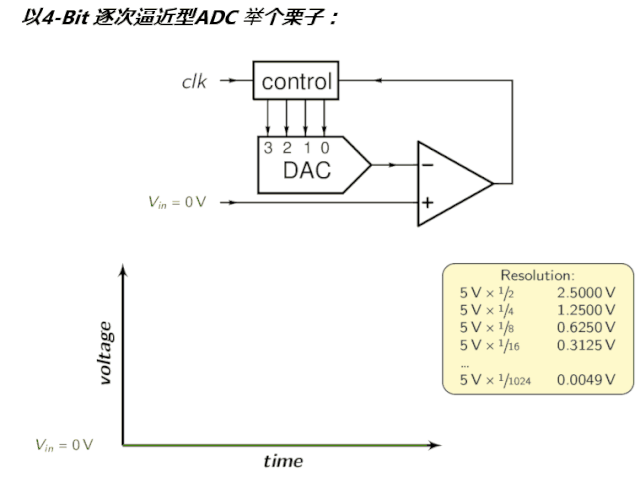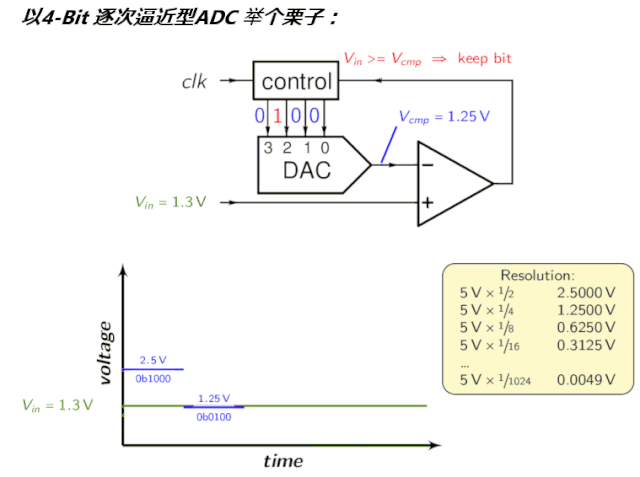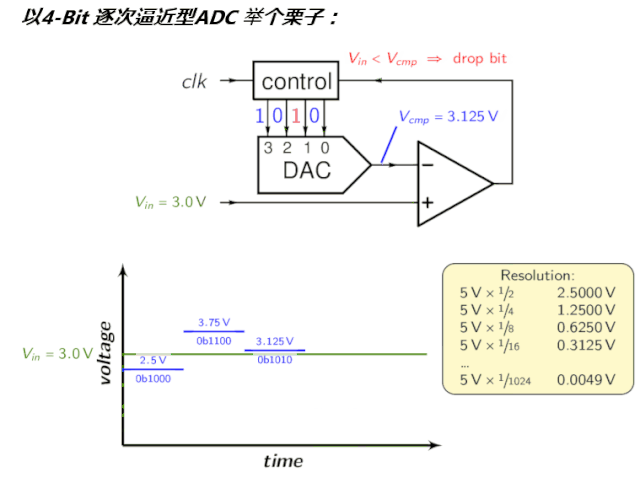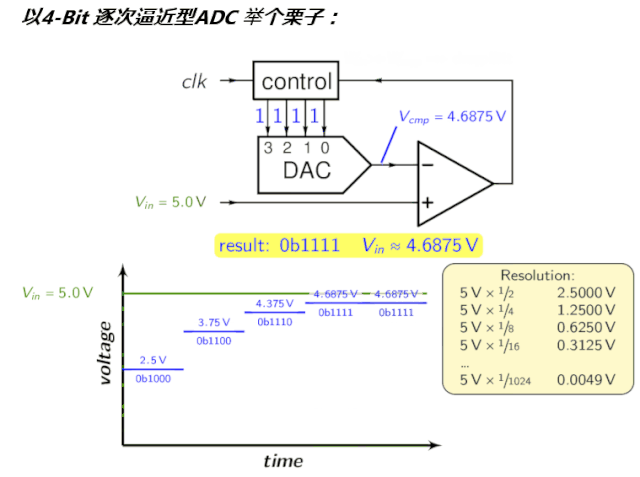
给你一个nn的矩阵,然后判断是否是magic的
如何是magic的呢?只要a[i][j]=a[j][i],a[i][i]=0,a[i][j]<=max(a[i][k],a[k][j])对于所有的k
题解:
就正解是把这个矩阵抽象成一个完全图
然后这个完全图,a[i][j]表示i点向j点连一条a[i][j]的边
然后magic是什么意思呢?
就是任何一条路径中的最大边都大于等于a[i][j],那么翻译过来就是跑最小生成树的之后,i到j上的最大边大于等于a[i][j]
于是就这样做呗。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2505;
int a[maxn][maxn];
pair<int,pair<int,int> > d[maxn*maxn];
int n,tot,last;
int fa[maxn];
int fi(int x)
{return x == fa[x]?x:fa[x]=fi(fa[x]);
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++){fa[i]=i;for(int j=1;j<=n;j++){if(i==j&&a[i][j])return puts("NOT MAGIC");if(a[i][j]!=a[j][i])return puts("NOT MAGIC");if(i>j)d[tot++]=make_pair(a[i][j],make_pair(i,j));}}sort(d,d+tot);for(int i=0;i<tot;i++){if(i+1<tot&&d[i].first==d[i+1].first)continue;for(int j=last;j<=i;j++){int p1 = fi(d[j].second.first);int p2 = fi(d[j].second.second);if(p1==p2)return puts("NOT MAGIC");}for(int j=last;j<=i;j++){int p1 = fi(d[j].second.first);int p2 = fi(d[j].second.second);fa[p2]=p1;}last=i+1;}puts("MAGIC");
}