【MATLAB】符号数学计算(七):符号微积分、符号微分方程求解、符号代数方程求解
一、符号表达式的极限
- limit(F,x,a):求当
时,符号表达式F的极限。
- limit(F,a):符号表达式F采用默认自变量(可由函数findsym求得),该函数求F的自变量趋于a时的极限值。
- limit(F):符号表达式采用默认变量,并以a=0作为自变量的趋近值。
- limit(F,x,a,'right')或limit(F,x,a,'left'):分别求符号表达式的左极限和右极限。
>> syms x
>> f1=sym('(cos(x)+sin(x)-x)/x');
>> limit(f1,x,inf)ans =-1>> limit(f1,x,-inf)ans =-1>> limit(f1,x,0)ans =NaN>> f2=sym('(sin(x)-x)/x')f2 =-(x - sin(x))/x>> limit(f2,x,0,'right')ans =0>> limit(f2,x,0,'left')ans =0二、符号表达式的微分
功能函数diff可以完成一元或多元函数任意阶数的微分。
对于自变量的个数多于一个的符号矩阵,微分为Jocabian矩阵,采用功能函数Jacobian实现。
1、diff函数
- diff(S,'v'):将符号“ v ”视作变量,对符号表达式或者符号矩阵求取微分。
- diff(S,n):将S中的默认变量进行n阶微分运算,其中默认变量可用findsym函数确定。
- diff(S,'v',n):将符号“ v ”视作变量,对符号表达式或矩阵S进行n阶微分运算。
2、jacobian函数
- R=jacobian(w,v):其中w是一个符号列向量,v是指定进行变换的变量所组成的行向量。
(第一个参数必须是列向量,第二个参数必须是行向量)
>> syms x y z;
>> f1=sym('exp(x*sin(y))+log(z)');
>> diff(f1,x)ans =exp(x*sin(y))*sin(y)>> diff(f1,y)ans =x*exp(x*sin(y))*cos(y)>> diff(f1,z)ans =1/z>> diff(f1,x,2)ans =exp(x*sin(y))*sin(y)^2>> f2=sym('[x^2+y^2;y*z]')f2 =x^2 + y^2y*z>> J=jacobian(f2,[x,y])J =[ 2*x, 2*y]
[ 0, z]三、符号表达式的积分
- R=int(S):用默认变量求符号表达式S的不定积分,默认变量可用函数findsym确定。
- R=int(S,v):用符号标量v作为变量求符号表达式S的不定积分。
- R=int(S,a,b):符号表达式采用默认变量,该函数求默认变量从a到b时符号表达式S的定积分值。如果S是符号矩阵,那么积分将对各个元素分别进行。
- R=int(S,v,a,b):用符号标量v作为变量,求当v从a变到b时,符号表达式S的定积分值。
>> syms x y
>> f1=sym('x+x^-1');
>> int(f1)ans =log(x) + x^2/2>> f2=sym('x*y+(x*y)^-1')f2 =1/(x*y) + x*y>> int(f2,y)ans =log(y)/x + (x*y^2)/2>> int(f1,1,2)ans =log(2) + 3/2>> int(f2,y,1,2)ans =(3*x)/2 + log(2)/x四、符号表达式的级数求和
- r=symsum(s,a,b):求符号s表达式中默认变量从a变到b时的有限和。
- symsum(s,v,a,b):求符号s表达式中变量v从a变到b时的有限和。
>> syms x y n
>> f1=sym('x^2')f1 =x^2>> symsum(f1,0,n-1)ans =(n*(2*n - 1)*(n - 1))/6>> f2=sym('x^n')f2 =x^n>> symsum(f2,n,0,inf)ans =piecewise([1 <= x, Inf], [abs(x) < 1, -1/(x - 1)])五、符号表达式的泰勒级数
- r=taylor(f):f是符号表达式,其变量采用默认变量,该函数返回f在变量等于0处作5阶泰勒展开时的展开式。
- r=taylor(f,n,v):符号表达式f以符号标量v作为自变量,返回f的n-1阶麦克劳林级数(即在v=0处的泰勒展开)展开式。
- r=taylor(f,n,v,a):返回符号表达式f在v=a处作n-1阶泰勒展开时的展开式。
>> syms x y
>> f1=sym('sin(x)/(2+sin(x))')f1 =sin(x)/(sin(x) + 2)>> taylor(f1)ans =- (13*x^5)/480 + x^4/48 + x^3/24 - x^2/4 + x/2六、符号微分方程求解
函数dsolve用来求常微分方程的符号解。
在方程中用D表示一次微分,用D2、D3分别表示二次、三次微分运算。
D2y表示
- r=dsolve('eq1,eq2,...','cond1,cond2,...','v'):求由eq1,eq2,...指定的常微分方程的符号解。常微分方程以变量v作为自变量,参数cond1,cond2,...用于指定方程的边界条件或者初始条件。如果v不知道,将默认t为自变量。
- r=dsolve('eq1,eq2’,...,'cond1,cond2‘,...,'v')
七、符号代数方程求解:solve
- g=solve(eq):其中eq可以是符号表达式或者不带符号的字符串,求解方程eq=0
- g=solve(eq,var):求解方程eq=0,自变量是var
- g=solve(eq1,eq2,...,eqn):求解符号表达式或不带符号的字符串eq1,eq2,...,eqn组成的方程组
>> syms x >> f=sym('a*x^2+b*x+c'); >> solve(f)ans =-(b + (b^2 - 4*a*c)^(1/2))/(2*a)-(b - (b^2 - 4*a*c)^(1/2))/(2*a)>> syms a x; >> f=sym('a*x^2+b*x+c'); >> solve(f,a)ans =-(c + b*x)/x^2>> syms x y >> f=sym('x^2+y^2=25'); >> f2=sym('x*y=12'); >> [x,y]=solve(f,f2)x =43-3-4y =34-4-3
相关文章:

Qt运行时中文乱码的解决办法
QT5的解决办法,在类之前添加: #pragma execution_character_set("utf-8")QT4解决办法: QTextCodec::setCodecForLocale(QTextCodec::codecForLocale());转载于:https://www.cnblogs.com/bjxingch/articles/9992998.html
更换yum的源为阿里云或者网易
1.备份原本的yum源: #mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup 2.下载阿里云的yum源: CentOS6,CentOS7,CentOS8下对应的即可 wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Ce…

socket编程:多路复用I/O服务端客户端之poll
一. 关于poll对于IO复用模型,其优点无疑是免去了对一个个IO事件就绪的等待,转而代之的是同时对多个IO数据的检测,当检测等待的事件中至少有一个就绪的时候,就会返回告诉用户进程“已经有数据准备好了,快看看是哪个赶紧…

【MATLAB】符号数学计算(八):符号分析可视化
一、funtool分析界面 在命令行窗口中输入: funtool 这里就说一下第四排: Insert:把当前激活窗的函数写入列表Cycle:依次循环显示fxlist中的函数Delete:从fxlist列表中删除激活窗的函数Reset:使计算器恢复…

java 根据实体对象生成 增删改的SQL语句 ModelToSQL
2019独角兽企业重金招聘Python工程师标准>>> java 根据实体对象生成 增删改的SQL语句 ModelToSQL 转载于:https://my.oschina.net/miaojiangmin/blog/2907010
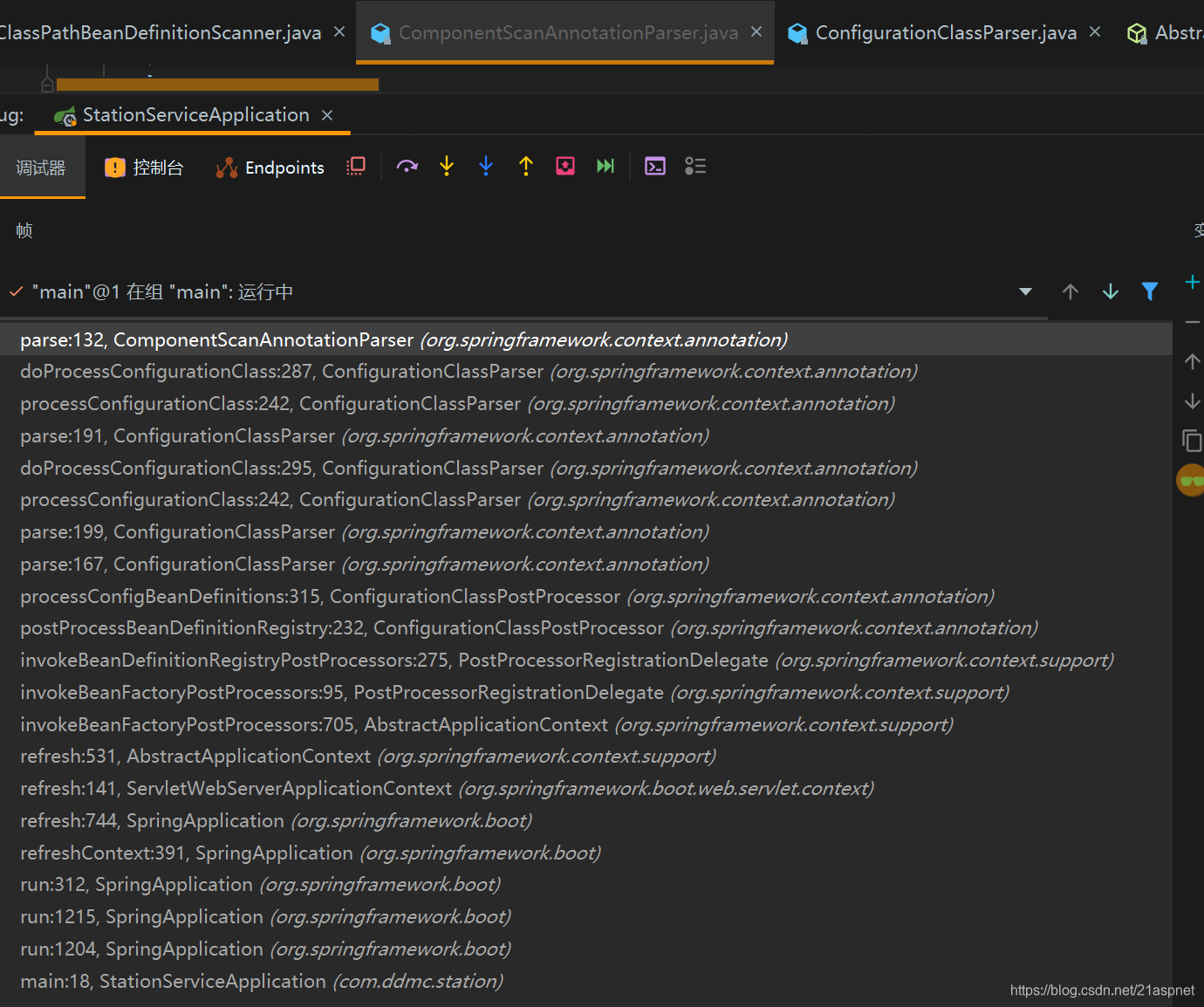
深入浅出SpringBoot源码分析
Spring源码非常多,不要迷失在源码的汪洋大海里,抓住主要脉络,有需要再研究即可。 Bean的初始化 1.发现所有的bean ComponentScanAnnotationParser.parse()调用doScan()扫包 这里只是扫用户定义的bean,系统的自然不用扫 ClassPathBeanDefinitionScanner.doScan protected…

HBase基本知识
为什么80%的码农都做不了架构师?>>> 概述 HBase 特性: 强一致性读写: HBase 不是 "最终一致性(eventually consistent)" 数据存储. 这让它很适合高速计数聚合类任务。自动分片(Automatic sharding): HBase 表通过region分布在集群…

【编程题】猜年龄
题目标题: 猜年龄 美国数学家维纳(N.Wiener) 智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。 一次,他参加某个重要会议,年轻的脸孔引人注目。于是有人询问他的年龄,他回答说: “我年龄的立方是个…

XenServer和VMware vSphere技术比较
此次将Citrix XenServer7.1和VMware ESXi 6.5从技术角度进行比较,并从企业角度对企业关心的项进行比较。主要包含市场地位、服务器虚拟化底层稳定性、管理架构、兼容性上进行分析。 市场地位 VMware在虚拟化的地位类似于大型存储中的EMC、小型机中IBM、网络中的思科…

阿里巴巴开源的缓存框架JetCache创建缓存
官网:https://github.com/alibaba/jetcache/wiki/CacheAPI_CN ======================= 多层嵌套缓存无效的问题: https://github.com/alibaba/jetcache/issues/424 某个service的方法加缓存注解,然后引用同一个类的另一个加缓存注解service的方法,这样必须在类里面注入…

【Python】百度翻译的爬虫实现(前篇)
该程序只能实现中文到英文的翻译 import requestsimport jsonurl "http://fanyi.baidu.com/basetrans"query_str input("请输入要翻译成英文的内容:")data{ "query": query_str,"from": "zh","to"…

github每次推送都要输入用户名和密码
/****************************************************************************** github每次推送都要输入用户名和密码* 说明:* 今天开始使用github管理一些东西,但是每次提交都出现要输入用户名和密码,* 这简直让人…

ELASTIC SEARCH 性能调优
ELASTICSEARCH 性能调优建议 创建索引调优 1.在创建索引的使用使用批量的方式导入到ES。 2.使用多线程的方式导入数据库。 3.增加默认刷新时间。 默认的刷新时间是1秒钟,这样会产生太多小的SEGMENT,导致未来的合并压力,如果调整这个大小&…

Android开源中国客户端学习 (自定义View)左右滑动控件ScrollLayout
左右滑动的控件我们使用的也是非常多了,但是基本上都是使用的viewpager 等 android基础的控件,那么我们有么有考虑过查看他的源码进行定制呢?当然,如果你自我感觉非常好的话可以自己定制一个,osc的ScrollLayout就是自己定义的View 和Viewpager的区别还是不小的 代码不是很多不…

【Python】有道翻译的爬虫实现(前篇)
import requestsimport jsonurl "http://fanyi.youdao.com/translate_o?smartresultdict&smartresultrule"data {"i": "我喜欢学习", "from": "AUTO", "to": "AUTO", "smartresult":&q…
自动生成纯文本表格的工具
https://tableconvert.com/?outputtext 有时候需要写文档的时候生成这种纯文本表格,这个工具真的很方便,贴上数据就可以了。

《Java编程思想》笔记13.字符串
点击进入我的博客 字符串操作是计算机程序设计中最常见的行为 13.1 不可变String String底层是由char[]实现的,是不可变的。看起来会改变String的方法,实际上都是创建了一个新的String对象,任何指向它的引用都不可能改变它本身的值。 13.2 重…

【Python】有道翻译的爬虫实现(后篇)
前面说到,有道翻译和百度翻译不同 (百度翻译是模拟iPhone手机,可能百度翻译用Pc端也会有类似的问题,有道翻译的User—Agent是Pc端) 每一次的salt和sign都不一样,这是什么原因产生的呢? 一、每…

Redis客户端JetCache的单机版和集群版的配置
jetcache基础应用参考这个:阿里巴巴开源的缓存框架JetCache创建缓存 1.JetCache的jedis配置 https://github.com/alibaba/jetcache/wiki/Config_CN jedis配置:apollo版 jetcache.remote.default.type = redis jetcache.remote.default.keyConvertor = fastjson jetcache.r…

5 分钟一次理解 Spring IOC !
今天我们分析一下 spring 的 IOC,梳理一下 IOC 和 DI 的概念与原理。在网上看到开涛有篇文章写的不错,提取其中一部分精华内容并做一些解读。 1.1.IOC是什么? Ioc—Inversion of Control,即“控制反转”,不是什么技术&…

工作两年的编程感想
2019独角兽企业重金招聘Python工程师标准>>> 工作已有两年了,两年不长也不短了,程序员的辛酸苦乐也都体验了一些,故写此博客既为留念,也为接下来的两年留下一个参考点。 首先需要声明的是,本人的工作是Java…

微服务重构心得
现在都在做微服务,看起来就是做服务拆分比较简单,但是实际上真正重构起来又遇到许许多多的问题。 微服务重构常见问题 1.领域驱动模型的困扰 比如听到很多理论比如领域驱动,那么到底需要不需要学习或者使用领域驱动呢? 2.系统的复杂性 重构的时候发现系统之间调用非常…

【Python】百度翻译的爬虫实现(后篇)
这个程序可以实现中英文的自动识别然后进行翻译 看着程序就很好理解。 import requestsimport jsonclass Translation():翻译def __init__(self,content):self.content contentself.url "http://fanyi.baidu.com/basetrans"self.headers {"User-Agent"…
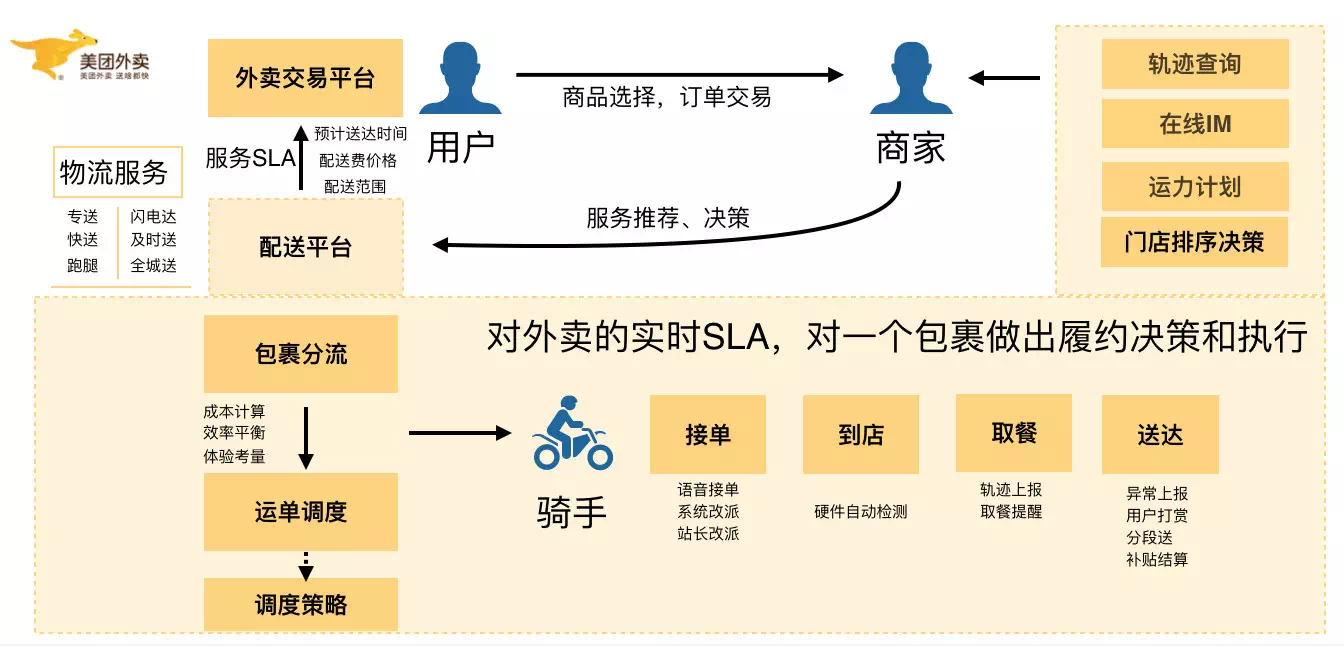
美团即时物流的分布式系统架构设计
背景 美团外卖已经发展了五年,即时物流探索也经历了3年多的时间,业务从零孵化到初具规模,在整个过程中积累了一些分布式高并发系统的建设经验。最主要的收获包括两点: 即时物流业务对故障和高延迟的容忍度极低,在业务复…
Intellij IDEA单元测试提示Test events were not received
Intellij IDEA单元测试时提示Test events were not received 也就是可以运行test方法,也提示成功,但是看不到具体的执行结果。 Intellij IDEA从2019.2.1版本开始,会将Gradle管理的项目的测试代码,默认使用Gradle来运行࿰…

Linux下task_struct详解
背景:为了管理进程,操作系统必须对每个进程所做的事情进行清楚地描述,为此,操作系统使用数据结构来代表处理不同的实体,这个数据结构就是通常所说的进程描述符或进程控制块。在linux系统中,这就是task_stru…

【Python】数据提取xpath和lxml模块(豆瓣电影排行榜的爬虫)
xpath xpath:一门从html中提取数据的语言 xpath语法 1、选择节点(标签) /html/head/meta :能够选中html下的head下的所有的meta标签 2、// :能够从任意节点开始选择 //li:当前页面上所有的li标签 //html/head/link &a…

qt5.6.3下使用firebird
有人把firebird比作数据库界的瑞士军刀,想学习一下其在QT5.6中的使用,于是便开始了一场自己挖坑,自己埋的旅程。 环境说明:win7 64位QT5.6 mingw4.9 32位(好像官网上也没有64位,当然mingw也是32位的&#x…

【Python】数据提取xpath和lxml模块(糗事百科的爬虫)
程序中用到的一些零碎知识点: 一、列表推导式:帮助我们快速生成一堆数据的列表 1、format:字符串格式化的一种方式 >>> ["10月{}日".format(i) for i in range(1,10)] [10月1日, 10月2日, 10月3日, 10月4日, 10月5日, 1…
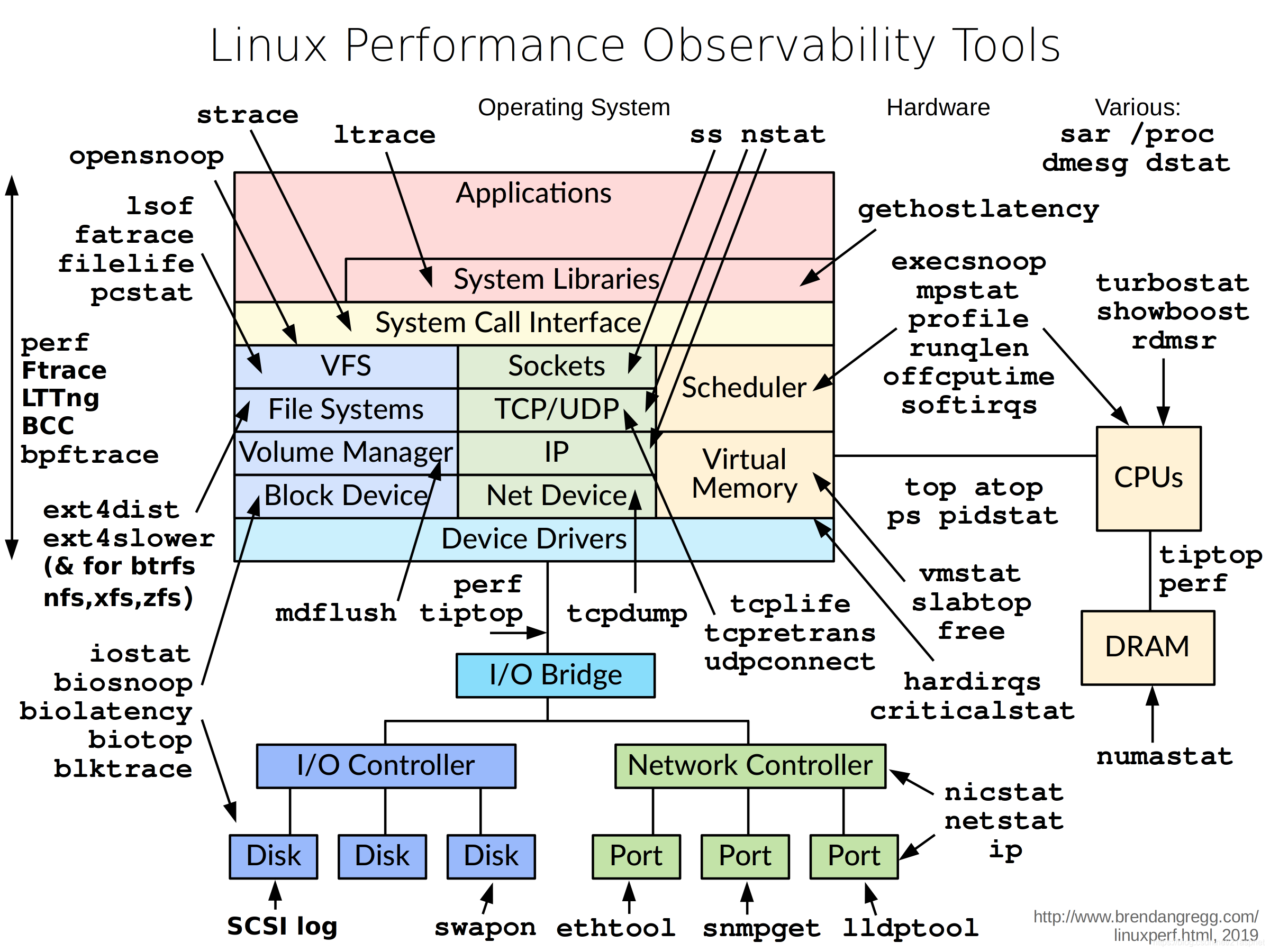
Linux Performance
性能专家Brendan Gregg的网站。 Linux性能 该页面链接到我创建的各种Linux性能材料,包括右侧的工具图。它们使用大字体来适合滑盖。您也可以将它们打印出来用于办公室墙壁。它们显示:Linux可观察性工具, Linux静态性能分析工具,…
