php源码安全加密的前世今生,本想发在教程区中.不知道怎么发,就写在这里面吧.
PHP加密,解密是一直的话题,本人菜鸟,今天就简单向大家介绍一下并说说其中原理.提供一些加密的混淆算法.
一\PHP的加密总体上来说分以下2种:
1\扩展组件类加密,代表有:zend\ionCube\SG\php_screw\bcompiler\BZ2等.
2\免扩展加密:php某盾等为代表的一批.
二\他们的安全性?
组件类加密:对于扩展加密,ZEND类为代表的是先编译成opcode再压缩执行.理论上没办法得到源代码.现在有一些ZEND破解,是通过OPCODE逆向转回PHP原代码,好的逆向效果在98%以上.不可能百分百,而php_screw等为代表的加密组件,是对源代码进地xor加密,DES加密等等. 在运行时要先解密,这样的代码是可以百分百被破解的.
免组件类加密:PHP某盾们,这一些都是在原有PHP代码上面增加一个外壳,类似于NET程序的加壳方法.执行时先通过壳来完成对原始代码的base64 eval 解压缩等操作.最终通过Eval执行. 最致命此类代码可被劫持eval百分百还原.
三\什么样的加密才安全?
不加密才最安全.呵...这个没说一样.不过有一个想法,可以增加解密的难度.简要流程如下:
加密过程:PHP源代码->PHP代码混淆器->加密(免组件外壳或组件加密)->加密成品源码.
执行过程:加载程序(免组件外壳或组件加密)->PHP混淆代码->执行代码.
通过上面流程,我们可以看到因为PHP代码进行了混淆处理,所以被得到的代码是乱的.这样的代码还是可以执行,但会给阅读者造成不易读的情况.另外,加载的程序即外壳的安全性至关重要.好的外壳,才是保护程序的关键.
对一源代码的混淆,可以操作的混淆内容有:PHP变量\PHP用户函数\PHP系统函数\PHP类名\PHP字符串,均可以完成加密.有人说过,这样混淆效果也不好啊,如何更变态?PHP支持变量名是ASCII码的127-255,而这一些字符在编辑器中看全是汉字乱码. 这样就可以增加难度性.
四\加密要付出,执行要代价!
如果只是简单的加密函数名\变量名还好,如果对字符串进行了加密保护.在进行每一次字符串操作时均需要执行一次解密操作.会消耗时间,影响系统执行的性能.到使用哪一种加密您值得考虑.
本人网址:http://www.phpjiami.com 欢迎交流,有砖的轻拍.
php源码安全加密之PHP混淆算法.
相关文章:

Element 2.6.0 发布,基于 Vue 2.0 的桌面端组件库
开发四年只会写业务代码,分布式高并发都不会还做程序员? Element 2.6.0 发布了,Element 是一套为开发者、设计师和产品经理准备的基于 Vue 2.0 的桌面端组件库,提供了配套设计资源,帮助你的网站快速成型。由饿了么公…
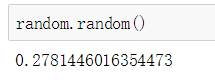
【Python】随机函数
import random 1、random.random() 2、random.uniform(a,b) 3、random.randint(a,b) 4、random.randrange([start],stop[, step]) 5、random.choice(sequence) 6、random.shuffle(x[, random]) 7、random.sample(sequence,k) import random 1、random.random() 返回随…

IOS/Android模拟器运行APP调试方法
真机不是那么好获取的,模拟器用起来更方便 ios 安装ios-sim 安装 ios-sim,获取 APP 完整的product的文件包。 $ npm i -g ios-sim 启动app # ios-sim launch *.app - -devicetypeid 本地模拟器支持机型类型 id $ ios-sim launch **/BaiduBoxApp.app --d…
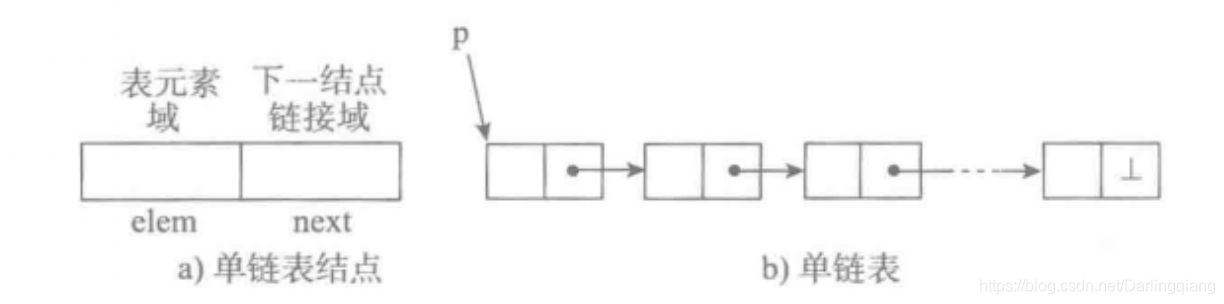
python数据结构与算法:单向链表
单链表:python实现及其对应的 增删查检 操作 ##################### P4.1-P4.8 单向链表 ########################### #coding:utf-8 class Node(object):def __init__(self,elem):self.elem elemself.next Noneclass SinglelinkList(object):""&quo…
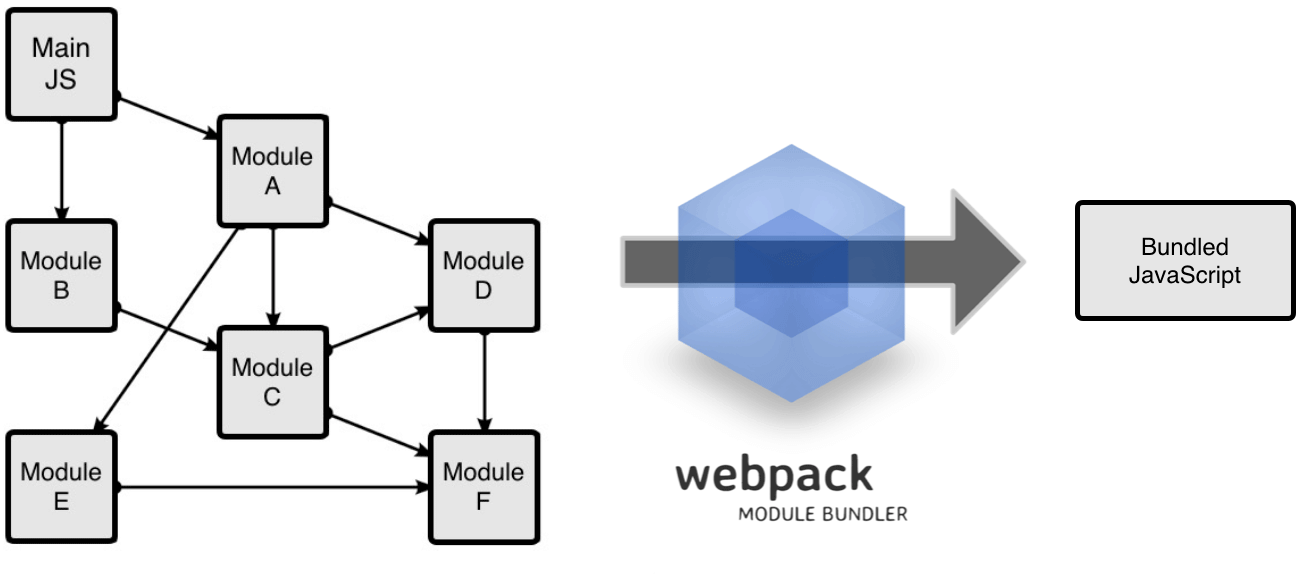
Vue性能优化:如何实现延迟加载和代码拆分?
移动优先方法已经成为一种标准,但不确定的网络条件导致应用程序快速加载变得越来越困难。在本系列文章中,我将深入探讨我们在Storefront应用程序中所使用的Vue性能优化技术,你们也可以在自己的Vue应用程序中使用它们来实现快速加载。 Webpack…

GitHub怎样fork别人代码到自己仓库并进行贡献
在过程中可能遇到这个问题:https://www.cnblogs.com/q1104460935/p/8275833.html 这个博客应该可以解决 比如说现在有一个很牛逼的项目,我们进入项目地址, 想将这个项目复制到自己的github仓库,然后你还想将 仓库中的代码拉取到…

python数据结构与算法:单向循环列表
单向循环列表:python实现,及其对应的 增删查检 操作 ##################### P4.9-P4.12 循环链表 ########################### #coding:utf-8 class Node(object):def __init__(self,elem):self.elem elemself.next None class SinglecycleList(ob…

http权威指南-http连接管理
2019独角兽企业重金招聘Python工程师标准>>> HTTP连接管理 浏览器解析URL流程: 浏览器解析出域名;浏览器查询这个主机名的IP地址;浏览器获得端口号;浏览器发起到主机名IP地址端口的80连接;浏览器向服务器发…

在macos上基于python2.7安装PyQt5
在macos上基于python2.7安装PyQt5 在python3上面安装PyQt5是十分简单的,可是,在python2.7上安装这个东西,着实让人折腾了一把。要总结一下,年纪大了,记性不好。 首先要安装最新版的Qt和python2,命令如下&am…

python数据结构与算法:二分查找
二分查找:python 实现def binary_seaech(alist,item):"""二分查找 递归实现"""n len(alist)if n > 0:mid n // 2if alist[mid] item:return Trueelif item < alist[mid]:return binary_seaech(alist[:mid],item)else:retur…

使用maven镜像
综述 用maven做项目,最郁闷的莫过于某些依赖库下载不了。被墙了,你懂的。使用maven镜像仓库及其重要,特别是国内的镜像,可以有效缓解被墙疼痛。 常用的镜像 国外镜像 ibiblio.org <mirror> <id>ibiblio</id> &…

Jupyter Notebook 快捷键(基本)
Jupyter Notebook 快捷键 Jupyter Notebook 有两种键盘输入模式。编辑模式,允许你往单元中键入代码或文本;这时的单元框线是绿色的。命令模式,键盘输入运行程序命令;这时的单元框线是灰色。 命令模式 (按键 Esc 开启) Enter : …

关于二叉树的几个必须掌握的实现
The best way to end your fear is to face it yourself. 结束恐惧的最佳办法就是自己面对。本分分享了二叉搜索树的几种实现,由简入繁。说句题外话,马上又是金三银四的季节了,无论跳不跳槽,增加自己的知识储备总是没错的。从代码…
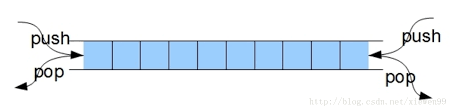
python数据结构与算法:队列与双端队列
双端队列: #################队列#################### #coding:utf-8 """ Deque() 创建一个空的双端队列 add_front(item) 从队头加入一个item元素 add_rear(item) 从队尾加入一个item元素 remove_front() 从队头删除一个item元素 remove_rear() 从…

view5.3登录桌面提示当前可用桌面资源不足
问题描述:用户反馈有个桌面经常提示当前可用桌面资源不足,开始的时候反复重启还可以使用,今天发现彻底无法登录了。解决方法:首先登录到view administrator管理平台查看该桌面发现状态是可用,说明桌面正常,…

【HDU】4706 Children's Day(模拟)
http://acm.hdu.edu.cn/showproblem.php?pid4706 该题没有输入,直接输出不同形状大小的N,在输出不同形状N的时候是要用到26个字母,并且是循环输出 #include <iostream>using namespace std;char map[60][60]; char a[] "abcdef…

详解原生AJAX请求demo(兼容IE5/6)
function createXHR(){ // 检测原生XHR对象是否存在if ( window.XMLHpptRequest ){// 如果存在就返回新实例return new XMLHpptRequest();} else { // 如果不存在就检测ActiveX对象// 兼容IE5/6return new ActiveXObject(Microsoft.XMLHttp);} }// 在所有的浏览器中创建XHR对象…

【POJ】3268 Silver Cow Party (将有向图的边反转)
问题链接:http://poj.org/problem?id3268 【问题描述】 One cow from each of N farms (1 ≤ N ≤ 1000) conveniently numbered 1…N is going to attend the big cow party to be held at farm #X (1 ≤ X ≤ N). A total of M (1 ≤ M ≤ 100,000) unidirectio…

项目管理深入理解08--成本管理
成本管理一章非常的重要,尤其是对于程序员来说,这方面非常的薄弱,但这部分知识无论是在项目管理中还是日常生活中都灰常重要,不然很难成为一个财务自由的程序员。此外,由于财务方面知识点比较多,特增加经济…
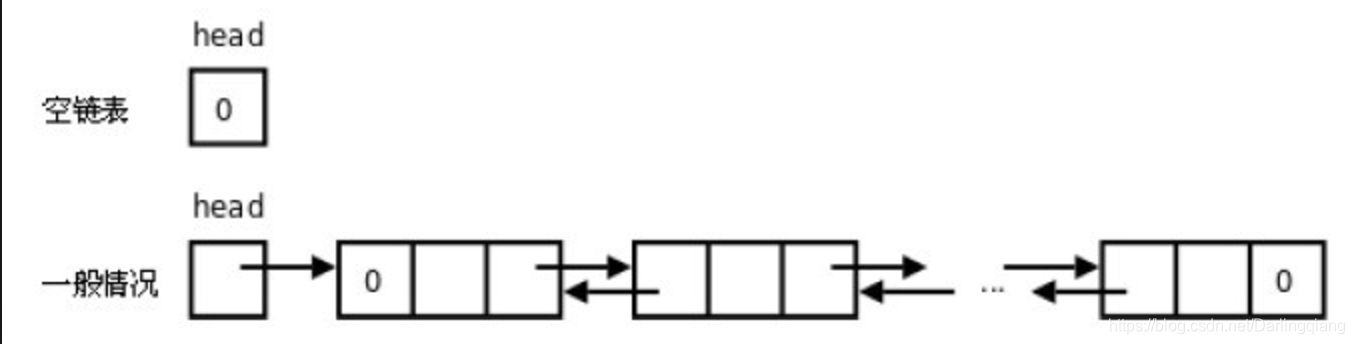
python数据结构与算法:双向链表
双向链表: ###################### P4.13-P4. 双向链表 ########################### # import singlelinkListclass Node(object):def __init__(self,item):self.elem itemself.next Noneself.prev None# class DoublelinkList(singlelinkList): #继承 class …

如何开发一个区块链应用程序
区块链是一项巧妙的发明,有望使数字世界更加安全和分散。通过允许数字信息的分发而不是复制,区块链技术创建了一种新型互联网。最初是为数字货币比特币而设计的,现在科技界正在寻找该技术的其他潜在用途。在不久的将来,我们将看到…
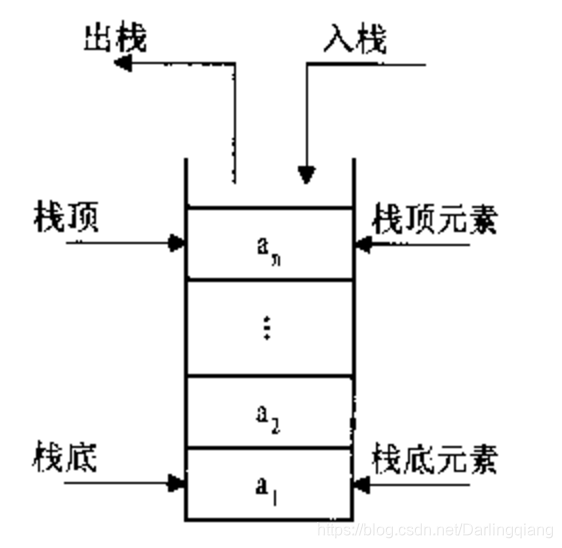
python数据结构与算法:栈
栈: Stack() 创建一个新的空栈 push(item) 添加一个新的元素item到栈顶 pop() 弹出栈顶元素 peek() 返回栈顶元素 is_empty() 判断栈是否为空 size() 返回栈的元素个数 Stack() 创建一个新的空栈 push(item) 添加一个新的元素item到栈顶 pop() 弹出栈顶元素 peek(…

【PAT (Basic Level) 】1014 福尔摩斯的约会 (20 分)
大侦探福尔摩斯接到一张奇怪的字条: 我们约会吧! 3485djDkxh4hhGE 2984akDfkkkkggEdsb s&hgsfdk d&Hyscvnm大侦探很快就明白了,字条上奇怪的乱码实际上就是约会的时间星期四 14:04,因为前面两字符串中第 1 对相同的…

菜鸟物流云是如何帮助快递合作伙伴解决双11巨大业务负荷的?
物流云双11 双11前,菜鸟物流云共接入12家合作伙伴,全部参加双11大促活动,作为物流云的首次双11,尤其是经过了快递公司的大考经验,事实证明项目是靠谱的。 双11前已经整体上云的快递合作伙伴2家,韵达和天天&…

安装H3C的各种问题
HCL安装完成后,启动HCL失败;提示:“当前系统用户名中包含非ASCII字符”问题?HCL只能安装装在英文路径下,如果用户名为中文或者安装路径有中文目录,就会出现此问题,请确保系统用户名和安装路径中…
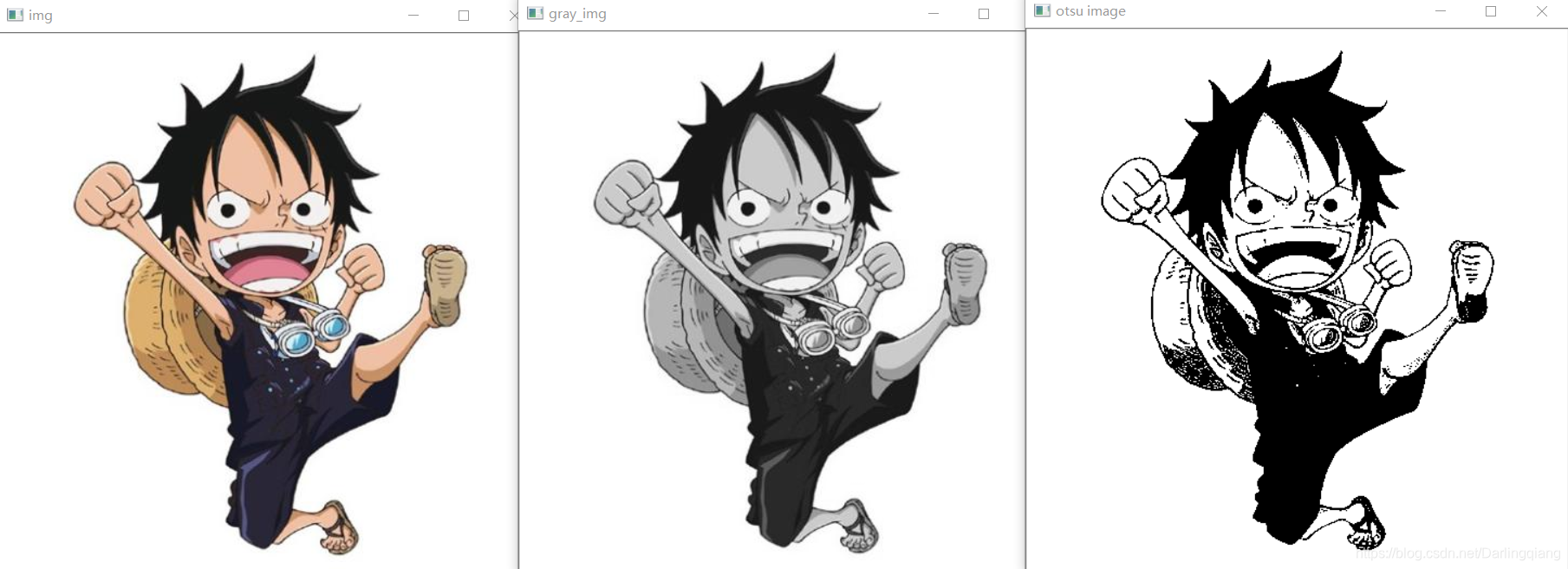
前景背景分割——ostu算法的原理及实现 OpenCV (八)
OpenCV 【八】——前景背景分割——ostu算法的原理及实现 实验结果代码实现实现原理参考资料实验结果 代码实现 #include<opencv2/opencv.hpp> #include<iostream> using namespace std; using namespace cv; //计算图像灰度直方图 Mat calcgrayhist(const Mat&am…

【PAT (Basic Level) 】1015 德才论 (25 分)
宋代史学家司马光在《资治通鉴》中有一段著名的“德才论”:“是故才德全尽谓之圣人,才德兼亡谓之愚人,德胜才谓之君子,才胜德谓之小人。凡取人之术,苟不得圣人,君子而与之,与其得小人࿰…

浏览器启动外部软件
常可以看见使用浏览器代码启动本地应用的软件.例如qq、迅雷、等等.那么他们是怎么做到的呢? 它的奥秘:Register protocol 前言我们经常看到 tencent://..thunder://这两种开头的网址,往往觉得很奇怪,很想弄懂其中的原理,是如何实现的&#x…

Luogu P1082 同余方程(NOIP 2012) 题解报告
题目传送门 【题目大意】 求关于x的同余方程 ax≡1(mod b)的最小整数解。 【思路分析】 由同余方程的有关知识可得,ax≡1(mod b)可以化为axby1,此方程有解当且仅当gcd(a,b)1,于是就可以用欧几里得算法求出一组特解x0,y0。 那么x0就…

MATLAB【二】————图像做减法,批量文本处理,子图显示
clear; clc; close all;name_string ["1.5ms\100\" ];length strlength(name_string); [m,n] size(length);%%----------------------------- for num1:mstr name_string(num,1); figure(color, [1, 1, 1], position, [0, 0, 1800,800]); % 为区分边界&a…
