当前位置：首页 > 编程日记 > 正文

【POJ】3268 Silver Cow Party （将有向图的边反转）

编程日记 2024-10-13 21:00:01

问题链接：http://poj.org/problem?id=3268

【问题描述】

One cow from each of N farms (1 ≤ N ≤ 1000) conveniently numbered 1…N is going to attend the big cow party to be held at farm #X (1 ≤ X ≤ N). A total of M (1 ≤ M ≤ 100,000) unidirectional (one-way roads connects pairs of farms; road i requires Ti (1 ≤ Ti ≤ 100) units of time to traverse.

Each cow must walk to the party and, when the party is over, return to her farm. Each cow is lazy and thus picks an optimal route with the shortest time. A cow’s return route might be different from her original route to the party since roads are one-way.

Of all the cows, what is the longest amount of time a cow must spend walking to the party and back?

【输入描述】

Line 1: Three space-separated integers, respectively: N, M, and X

Lines 2… M+1: Line i+1 describes road i with three space-separated integers: Ai, Bi, and Ti. The described road runs from farm Ai to farm Bi, requiring Ti time units to traverse.

【输出描述】

Line 1: One integer: the maximum of time any one cow must walk.

【样例输入】

4 8 2

1 2 4

1 3 2

1 4 7

2 1 1

2 3 5

3 1 2

3 4 4

4 2 3

【样例输出】

10

注意：
题不止求一个点的最短路，

一个是从牛X的位置返回它们各自的位置的最短距离，我写的是xa函数，这个就是简单的Dijkstra算法的应用
牛从它们自己的点去牛x的位置，这个有两种方法
- 以每一个点为起点计算从该点到x的最短距离，如果数据量太大的，就会超时。
- 将有向边反转，这个和乘以2是不一样的概念，因为图都已经不一样了，可以这么想，在1的情况下，从x返回，现在要从各个顶点去x，那样的路径是不是相当于把边反转以后再从x回来是一样的，把边反转以后，有向图就变了，所以和乘以2不一样。

#include <iostream>
#include <queue>
#include <vector>
#include <cstdio>
#include <algorithm>using namespace std;const int maxn = 1005;
const int inf = 0x3f3f3f3f;struct node
{int to;int cost;node(int t,int c){to = t;cost = c; }friend bool operator < (struct node a,struct node b){return a.cost > b.cost;}
};int d1[maxn];
int d2[maxn];
int vis[maxn];
vector<node> v1[maxn];//从x返回 
vector<node> v2[maxn];//去x，将边的反转，即也是从x来求 
int n,m,x;void xa()//从x返回 
{fill(vis,vis+maxn,0);fill(d1,d1+maxn,inf);priority_queue<node> p;d1[x] = 0;p.push(node(x,0));while(p.empty()!=1){node t = p.top();p.pop();int pos = t.to;if(vis[pos])continue;vis[pos] = 1;for(int i=0;i<v1[pos].size();i++){node x = v1[pos][i];if(!vis[x.to] && d1[x.to]>(d1[pos]+x.cost)){d1[x.to] = d1[pos] + x.cost;p.push(node(x.to,d1[x.to]));}}}
}void ax()//将边反转 
{fill(vis,vis+maxn,0);fill(d2,d2+maxn,inf);priority_queue<node> p;d2[x] = 0;p.push(node(x,0));while(p.empty()!=1){node t = p.top();p.pop();int pos = t.to;if(vis[pos])continue;vis[pos] = 1;for(int i=0;i<v2[pos].size();i++){node x = v2[pos][i];if(!vis[x.to] && d2[x.to]>d2[pos]+x.cost){d2[x.to] = d2[pos] + x.cost;p.push(node(x.to,d2[x.to])); }}}
} int main ()
{int i,a,b,c;while(scanf("%d%d%d",&n,&m,&x)!=EOF){for(i=0;i<n;i++){d1[i] = inf;d2[i] = inf;v1[i].clear();v2[i].clear();} for(i=0;i<m;i++){scanf("%d%d%d",&a,&b,&c);v1[a].push_back(node(b,c));//去的边 v2[b].push_back(node(a,c));//边的反转 }xa();ax();int ans = -1;for(i=1;i<=n;i++){ans = max(ans,d1[i]+d2[i]);}printf("%d\n",ans);}return 0;
}

下面的代码是没有将边反转，而是以每一个点为起点，计算到x的最短路

#include <iostream>
#include <queue>
#include <vector>
#include <cstdio>
#include <algorithm>using namespace std;const int maxn = 1005;
const int inf = 0x3f3f3f3f;struct node
{int to;int cost;node(int t,int c){to = t;cost = c; }friend bool operator < (struct node a,struct node b){return a.cost > b.cost;}
};int d1[maxn];
int dd[maxn];
int vis[maxn];
vector<node> v1[maxn];//从x返回 
int n,m,x;void xa()//从x返回 
{fill(vis,vis+maxn,0);fill(d1,d1+maxn,inf);priority_queue<node> p;d1[x] = 0;p.push(node(x,0));while(p.empty()!=1){node t = p.top();p.pop();int pos = t.to;if(vis[pos])continue;vis[pos] = 1;for(int i=0;i<v1[pos].size();i++){node x = v1[pos][i];if(!vis[x.to] && d1[x.to]>(d1[pos]+x.cost)){d1[x.to] = d1[pos] + x.cost;p.push(node(x.to,d1[x.to]));}}}
}int ax(int tem)
{int d2[maxn];fill(vis,vis+maxn,0);fill(d2,d2+maxn,inf);priority_queue<node> p;d2[tem] = 0;p.push(node(tem,0));while(p.empty()!=1){node t = p.top();p.pop();int pos = t.to;if(vis[pos])continue;if(pos==x)return d2[x];vis[pos] = 1;for(int i=0;i<v1[pos].size();i++){node x = v1[pos][i];if(!vis[x.to] && d2[x.to]>d2[pos]+x.cost){d2[x.to] = d2[pos] + x.cost;p.push(node(x.to,d2[x.to])); }}}return d2[x];
} int main ()
{int i,a,b,c;while(scanf("%d%d%d",&n,&m,&x)!=EOF){for(i=0;i<n;i++){d1[i] = inf;v1[i].clear();} for(i=0;i<m;i++){scanf("%d%d%d",&a,&b,&c);v1[a].push_back(node(b,c));//去的边 }xa();for(i=1;i<=n;i++){if(i==x)continue;dd[i] = ax(i);}int ans = -1;for(i=1;i<=n;i++){ans = max(ans,d1[i]+dd[i]);}printf("%d\n",ans);}return 0;
}

https://www.dkcj.cn/info/22911.html

【POJ】3268 Silver Cow Party （将有向图的边反转）

问题链接：http://poj.org/problem?id=3268

相关文章：

项目管理深入理解08--成本管理

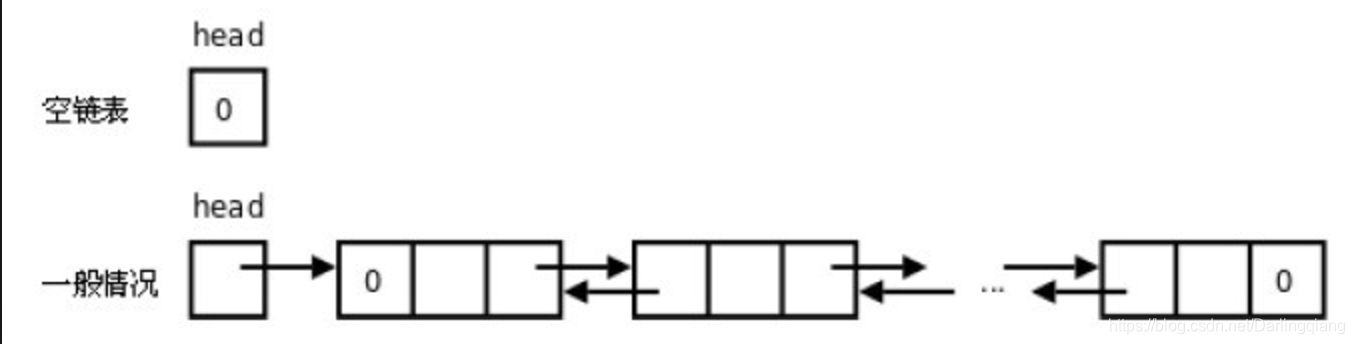
python数据结构与算法：双向链表

如何开发一个区块链应用程序

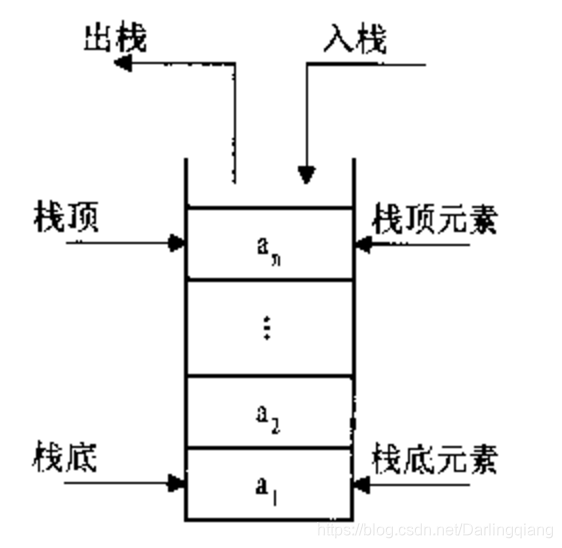
python数据结构与算法：栈

【PAT (Basic Level) 】1014 福尔摩斯的约会 (20 分)

菜鸟物流云是如何帮助快递合作伙伴解决双11巨大业务负荷的？

安装H3C的各种问题

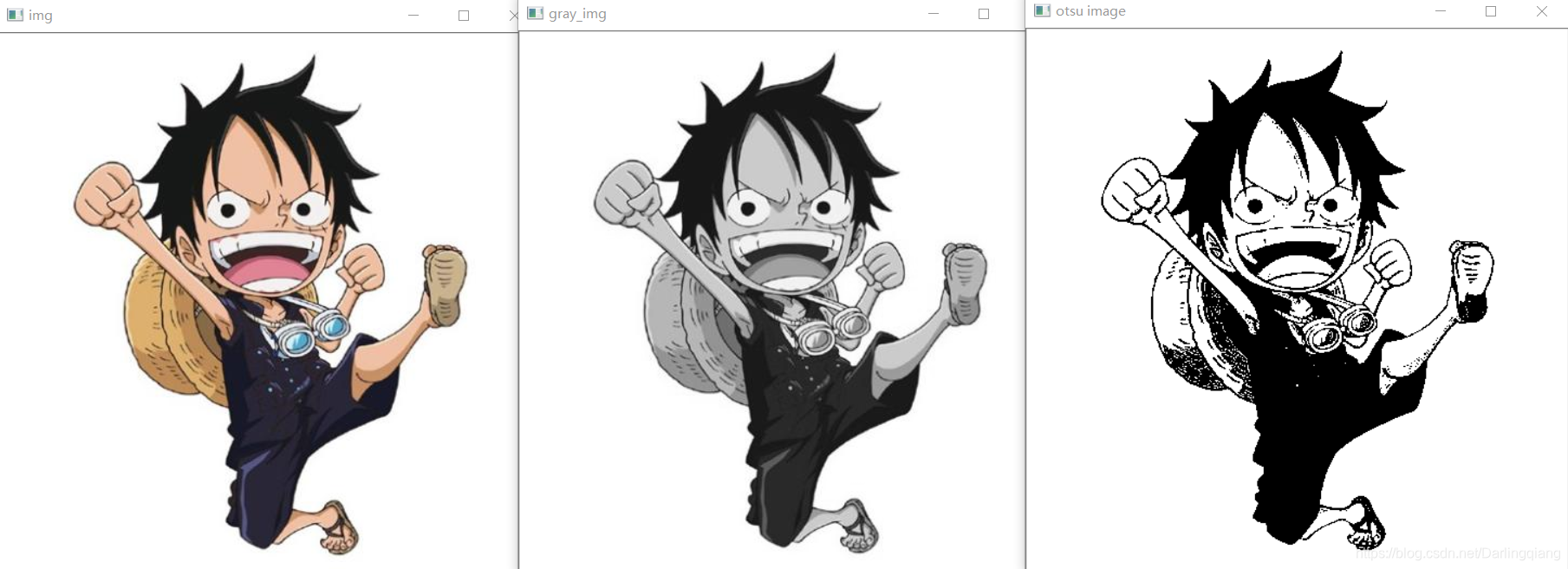
前景背景分割——ostu算法的原理及实现 OpenCV (八）

【PAT (Basic Level) 】1015 德才论 (25 分)

浏览器启动外部软件

Luogu P1082 同余方程(NOIP 2012) 题解报告

MATLAB【二】————图像做减法，批量文本处理，子图显示

与数据有关的问题

【PAT (Basic Level) 】1024 科学计数法 (20 分)

jsp 实栗 jsp + jdbc 登录

OpenCV 【十】——Gamma校正 ——图像灰度变化

Linux磁盘阵列技术详解（二）--raid 1创建

【PAT (Basic Level) 】1025 反转链表 (25 分)

C#关于窗体的传值

MATLAB【四】 ————批量适配图片信息与excel/txt等文档信息，批量移动拷贝图片，批量存图片中点和方框

mysql日志文件相关的配置【2】

【PAT (Basic Level) 】1028 人口普查 (20 分)

SW6206超级华为快充5V5A，全协议OPPO闪充、自带电量计量、LED 灯/数码管显示

bash脚本【一】——批量处理文件

【PAT (Basic Level) 】1030 完美数列 (25 分)

运营商劫持处理

oracle维护数据的完整性

MATLAB【五】———— matlab 调用C++生成exe文件，高斯核函数

REACT day 1

win10+Chrome浏览器截长图方法