如何利用 C# 实现 K-D Tree 结构?
我的朋友海伦一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的人选,但她没有从中找到喜欢的人。经过一番总结,她发现曾交往过三种类型的人:
- 不喜欢的人
- 魅力一般的人
- 极具魅力的人
尽管发现了上述规律,但海伦依然无法将约会网站推荐的匹配对象归入恰当的分类。她觉得可以在周一到周五约会哪些魅力一般的人,而周末则更喜欢与那些极具魅力的人为伴。海伦希望我们的分类软件可以更好地帮助她匹配对象划分到确切的分类中。此外海伦还收集了一些约会网站未曾记录的数据信息,她认为这些数据更有助于匹配对象的归类。
海伦收集约会数据已经有一段时间,她把这些数据存放在文本文件datingTestSet.txt中,每个样本占据一行,总共有1000行。海伦的样本主要包含以下3种特征:
- 每年获得的飞行常客里程数
- 玩视频游戏所耗费时间百分比
- 每周消费的冰激凌公升数
以上是《机器学习实战》中介绍 K 最邻近算法给出的示例,通过该示例我们可以了解到 K 最邻近算法应用的另一个场景:改善约会网站的配对效果。本次介绍 K-D 树是为了加速寻找给定节点的邻居节点,是提升 K 最邻近算法执行效率的一种改进。
我们首先介绍一下 K-D 树的基本原理,由于篇幅的限制,详细的理论部分可以参见对应的维基百科。
K-D 树
K-D 树(K 维树的简称)是一种用于在 K 维空间中组织点的空间划分数据结构。K-D 树是非常有用的一种数据结构,常用于涉及多维搜索键的搜索(比如,范围搜索和邻近搜索)。
K-D 树是一个二叉树,其中每个节点都是一个 K 维点。每个非叶节点都可以被认为是隐式生成一个分裂超平面,将空间分成两部分,称为半空间。该超平面左侧的点表示该节点的左子树,而该超平面右侧的点则表示为右子树。超平面方向的选择方法如下:树中的每个节点都与一个 K 维相关联,超平面垂直于该维的轴。因此,例如,如果对特定的拆分选择了 X 轴,则子树中所有 X 值小于节点的点都将显示在左子树中,而所有 X 值较大的点都将显示在右子树中。在这种情况下,超平面将由点的 X 值设置,其法向量为单位 X 轴。
更详细的介绍,见维基百科:
https://en.wikipedia.org/wiki/K-d_tree

麦哈顿距离
更详细的介绍,见维基百科:
https://en.wikipedia.org/wiki/Taxicab_geometry

有了以上的基础,我们首先来定义 K-D 树节点的结构,然后定义邻居节点的结构,以及麦哈顿距离,最后给出 K-D 树的结构以及具体应用。
1. 定义K-D 树节点的结构
public class KDTreeNode<T>
{//分割轴public int Axis { get; set; }//节点值public double[] Position { get; set; }//标签值public T Value { get; set; }//左子树public KDTreeNode<T> Left { get; set; }//右子树public KDTreeNode<T> Right { get; set; }//是否为叶子节点public bool IsLeaf{get { return Left == null && Right == null; }}
}
2. 定义邻居节点的结构
public struct KDTreeNodeDistance<T> : IComparable, IComparable<KDTreeNodeDistance<T>>, IEquatable<KDTreeNodeDistance<T>>
{public double Distance { get; }public KDTreeNode<T> Node { get; }public KDTreeNodeDistance(KDTreeNode<T> node, double distance){this.Node = node;this.Distance = distance;}public int CompareTo(object obj){return Distance.CompareTo((KDTreeNodeDistance<T>)obj);}public int CompareTo(KDTreeNodeDistance<T> other){return Distance.CompareTo(other.Distance);}public bool Equals(KDTreeNodeDistance<T> other){return Distance == other.Distance && Node == other.Node;}
}
3. 定义麦哈顿距离
public sealed class Manhattan : IMetric<double[]>
{public double Distance(double[] x, double[] y){double sum = 0.0;for (int i = 0; i < x.Length; i++)sum += Math.Abs(x[i] - y[i]);return sum;}
}
4. 定义 K-D 树的结构
public class KDTree<T> : IEnumerable<KDTreeNode<T>>
{//距离public IMetric<double[]> Distance { get; set; } = new Euclidean();//树根public KDTreeNode<T> Root { get; }//节点个数public int Count { get; }//叶子节点个数public int Leaves { get; }//节点维数public int Dimensions { get; }public KDTree(double[][] points, T[] values, IMetric<double[]> distance, bool inPlace = false){if (points == null)throw new ArgumentNullException();if (points.Length == 0)throw new ArgumentException("创建树的点数不足。");if (values == null)throw new ArgumentNullException();if (distance == null)throw new ArgumentNullException();int leaves;Root = CreateRoot(points, values, inPlace, out leaves);Leaves = leaves;Distance = distance;Dimensions = points[0].Length;Count = points.Length;}public KDTree(double[][] points, bool inPlace = false){if (points == null)throw new ArgumentNullException();if (points.Length == 0)throw new ArgumentException("创建树的点数不足。");int leaves;Root = CreateRoot(points, null, inPlace, out leaves);Leaves = leaves;Dimensions = points[0].Length;Count = points.Length;}protected KDTreeNode<T> CreateRoot(double[][] points, T[] values, bool inPlace, out int leaves){if (points == null)throw new ArgumentNullException();if (values != null && points.Length != values.Length)throw new DimensionMismatchException("values");if (!inPlace){points = (double[][])points.Clone();if (values != null)values = (T[])values.Clone();}leaves = 0;int dimensions = points[0].Length;ElementComparer comparer = new ElementComparer();KDTreeNode<T> root = Create(points, values, 0, dimensions, 0, points.Length, comparer, ref leaves);return root;}private KDTreeNode<T> Create(double[][] points, T[] values,int depth, int k, int start, int length, ElementComparer comparer, ref int leaves){if (length <= 0)return null;int axis = comparer.Index = depth%k;Array.Sort(points, values, start, length, comparer);int half = start + length/2;int leftStart = start;int leftLength = half - start;int rightStart = half + 1;int rightLength = length - length/2 - 1;double[] median = points[half];T value = values != null ? values[half] : default(T);depth++;KDTreeNode<T> left = Create(points, values, depth, k, leftStart, leftLength, comparer, ref leaves);KDTreeNode<T> right = Create(points, values, depth, k, rightStart, rightLength, comparer, ref leaves);if (left == null && right == null)leaves++;return new KDTreeNode<T>(){Axis = axis,Position = median,Value = value,Left = left,Right = right,};}private void Nearest(KDTreeNode<T> current, double[] position, KDTreeNodeCollection<T> list){double d = Distance.Distance(position, current.Position);list.Add(current, d);double value = position[current.Axis];double median = current.Position[current.Axis];double u = value - median;if (u <= 0){if (current.Left != null)Nearest(current.Left, position, list);if (current.Right != null && Math.Abs(u) <= list.Maximum)Nearest(current.Right, position, list);}else{if (current.Right != null)Nearest(current.Right, position, list);if (current.Left != null && Math.Abs(u) <= list.Maximum)Nearest(current.Left, position, list);}}private void Nearest(KDTreeNode<T> current, double[] position,double radius, ICollection<KDTreeNodeDistance<T>> list){double d = Distance.Distance(position, current.Position);if (d <= radius)list.Add(new KDTreeNodeDistance<T>(current, d));double value = position[current.Axis];double median = current.Position[current.Axis];double u = value - median;if (u <= 0){if (current.Left != null)Nearest(current.Left, position, radius, list);if (current.Right != null && Math.Abs(u) <= radius)Nearest(current.Right, position, radius, list);}else{if (current.Right != null)Nearest(current.Right, position, radius, list);if (current.Left != null && Math.Abs(u) <= radius)Nearest(current.Left, position, radius, list);}}public KDTreeNodeCollection<T> Nearest(double[] position, int neighbors){KDTreeNodeCollection<T> list = new KDTreeNodeCollection<T>(neighbors);if (Root != null)Nearest(Root, position, list);return list;}public KDTreeNodeList<T> Nearest(double[] position, double radius){KDTreeNodeList<T> list = new KDTreeNodeList<T>();if (Root != null)Nearest(Root, position, radius, list);return list;} public IEnumerator<KDTreeNode<T>> GetEnumerator(){if (Root == null)yield break;Stack<KDTreeNode<T>> stack = new Stack<KDTreeNode<T>>(new[] {Root});while (stack.Count != 0){KDTreeNode<T> current = stack.Pop();yield return current;if (current.Left != null)stack.Push(current.Left);if (current.Right != null)stack.Push(current.Right);}}IEnumerator IEnumerable.GetEnumerator(){return GetEnumerator();}
} 5. K-D 树的应用
假设我们拥有以下点的集合:
double[][] points =
{new double[] {2, 3},new double[] {5, 4},new double[] {9, 6},new double[] {4, 7},new double[] {8, 1},new double[] {7, 2},
};
从这些数据点中创建K-D 树:
KDTree<int> tree = new KDTree(points);
我们可以手动导航这颗树:
KDTreeNode<int> node = tree.Root.Left.Right;
或者自动遍历这棵树,由于 KDTree<T> 实现了枚举器也即实现了迭代器模式,所以可以用 foreach 来遍历这棵树的数据。但对于普通的二叉树来说,通常使用前序遍历、中序遍历、后序遍历或者层次遍历的方式进行。
foreach (KDTreeNode<int> n in tree)
{double[] location = n.Position;Console.WriteLine(@"({0},{1})", location[0], location[1]);
}
可以得到如下的结果:
(7,2)
(9,6)
(8,1)
(5,4)
(4,7)
(2,3)
给定一个查询点(例如:(5,3)),我们还可以查询半径(欧氏距离 4.0)内靠近该点的其它点。
double[] query = new double[] {5, 3};
KDTreeNodeList<int> result = tree.Nearest(query, 4.0);
for (int i = 0, len = result.Count; i < len; i++)
{KDTreeNode<int> node = result[i].Node;Console.WriteLine(@"({0},{1})", node.Position[0], node.Position[1]);
}
可以得到如下的结果:
(7,2)
(5,4)
(2,3)
(8,1)
我们也可以使用其它的距离度量,比如麦哈顿距离:
double[] query = new double[] {5, 3};
tree.Distance = new Manhattan();
KDTreeNodeList<int> result = tree.Nearest(query, 4.0);
for (int i = 0, len = result.Count; i < len; i++)
{KDTreeNode<int> node = result[i].Node;Console.WriteLine(@"({0},{1})", node.Position[0], node.Position[1]);
}
可以得到如下的结果:
(7,2)
(5,4)
(2,3)
以及查询固定数量的相邻点,比如
KDTreeNodeCollection<int> neighbors = tree.Nearest(query, 3);
for (int i = 0, len = neighbors.Count; i < len; i++)
{KDTreeNode<int> node = neighbors[i].Node;Console.WriteLine(@"({0},{1})", node.Position[0], node.Position[1]);
}
可以得到如下的结果:
(5,4)
(2,3)
(7,2)
到此为止,用 C# 实现 K-D 树就介绍完了。在后台回复 20190312 可以得到,本篇开头说的 网站约会信息的数据集。大家把上面的代码看懂后,可以尝试的写一下,然后用这个数据集来测试自己的代码。
今天就到这里吧!See You!
相关文章:

[恩难到了]陨石的秘密
【描述】 公元19881231年,一颗巨大的陨石坠落在世界的政治文化中心cs。于是,灾难降临了,地球上出现了一系列反常的现象。当人们焦急万分的时候,一支由cs科学家组成的考察队赶到了出事地点。经过一番侦察,科学家们发现陨…

java培训学习阶段步骤讲解
目前的培训机构行业比较热门的IT技术就是java技术,java技术在近几年广受关注,java所涉及的技术知识也比较广泛,下面小编就为大家详细的介绍一下java培训学习多有哪几个阶段? java培训学习多有哪几个阶段: 第一阶段、Java设计和编…

资料分享:送你一本《机器学习实战》电子书!
这两天,各985高校发布了考研初试分数线。从中发现这两年大数据相关专业的分数线暴涨啊。没有400分估计心里都没底啊。可见大数据这个领域有多火爆!而机器学习是我们团队的一个主要方向,新加入的同学通常都是从《机器学习实战》这本书开始入门…

HDU 6091 - Rikka with Match | 2017 Multi-University Training Contest 5
思路来自 某FXXL 不过复杂度咋算的.. /* HDU 6091 - Rikka with Match [ 树形DP ] | 2017 Multi-University Training Contest 5 题意:给出N个点的树,求去边的方案数使得 去边后最大匹配数是M的倍数限制: N<5e4, M<200 分析ÿ…

在别的电脑上运行cg程序出现错误的解决办法
错误:没有找到cg.dll,因为这个应用程序未能启动。重新安装应用程序可能会修复此问题 解决方法:复制cg.dll到system32 、debug中 错误:没有找到cgGL.dll,因为这个应用程序未能启动。重新安装应用程序可能会修复此问题 解…
HTML在网页设计中是什么作用?
HTML是一种超文本传输协议,规定了浏览器与服务端之间数据传输的格式,是一种标识性的代码语言,它的中文翻译是“超文本标记语言”,主要是通过HTML标签对网页中的文本、图片、声音等内容进行描述。HTML提供了许多标签,如…

如何实现链接只能被点击一次
有时候,只希望网站某个链接只能被点击一次,怎么做呢?下面给出3中方法!第一种:利用JS在点击后把href变成#把taget变成空。 <p><a onclick"var that this;setTimeout(function(){that.removeAttribute(hr…

匿名类型和Object转换
.net中的匿名类型非常好用, 但是开发中遇到一个问题,当把匿名类型作为返回值的时候,会变成object类型,如果才能再转换能对应的匿名类型呢? 1 //返回匿名类型的函数, 会转换成object类型2 object ReturnAnonymous() {3 retur…

资料分享:送你一本《数据结构(C#语言版)》电子书!
对于信息类专业的学生而言,数据结构与算法是一门必修的课程。只有学好这门课程,熟练掌握线性表、栈、队列、树、图等基本结构,以及在这些结构上的各种算法,才能利用计算机去解决实际问题。 如何学好这门课程呢,给大家…

新手入门API测试必要了解的知识
什么是API?API是Application Programming Interface的简写。实现了两个或多个独立系统或模块间的通信和数据交换能力。 什么是API测试?API测试是不同于UI级自动化测试,其主要关注在系统架构的业务逻辑层,所以其主要关注不在于UI操作或用户感观上&#…

java监控多个线程的实现
场景:需要启动多线程处理事情,而在所有事情做完之后,需要修改系统状态;那么如何判断所有线程(事情)都做完了呢?这就需要判断所有当前运行的线程状态了。 代码 importjava.util.concurrent.Count…

如何利用 C# 实现神经网络的感知器模型?
前几天我们介绍了 如何利用 C# 对神经网络模型进行抽象,在这篇图文中,我们抽象了单个神经元 Neuro,网络层 Layer,网络结构 Network,激活函数 IActivationFunction,以及监督学习 ISupervisedLearning 和非监…

JPA增删改查,
2019独角兽企业重金招聘Python工程师标准>>> 1. //And --- 等价于 SQL 中的 and 关键字 public List<User> findByHeightAndSex(int height,char sex); 2. // Or --- 等价于 SQL 中的 or 关键字 public List<User> findByHeightOrSex(int height,cha…

Java新手会遇到的三大误区,一定要避免!
很多学习java技术的学员都是零基础学员,之前对java技术一点都不了解,所以java新手在学习java技术的时候很容易进入误区,下面小编分享的Java新手会遇到的三大误区,一定要避免! 作为目前最为广泛的网络编程语,Java凭借其…
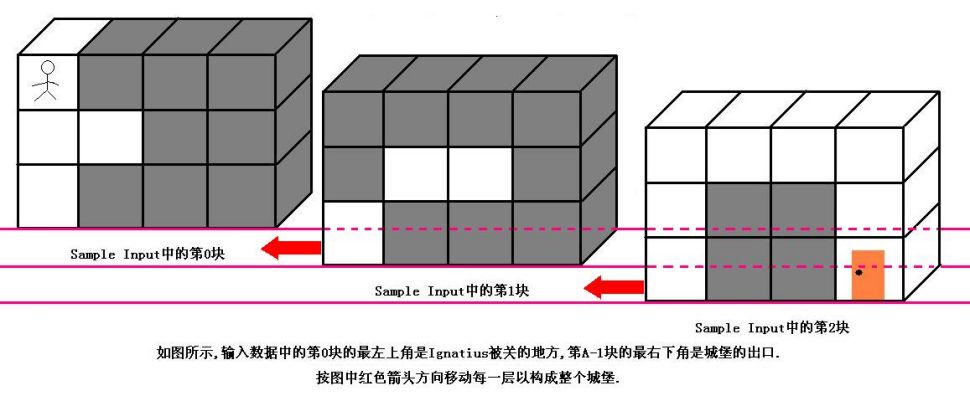
[ACM] hdu 1253 胜利大逃亡 (三维BFS)
胜利大逃亡 Problem DescriptionIgnatius被魔王抓走了,有一天魔王出差去了,这但是Ignatius逃亡的好机会.魔王住在一个城堡里,城堡是一个A*B*C的立方体,能够被表示成A个B*C的矩阵,刚開始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,如今知道魔王将在T分钟后…

如何利用 C# 爬取带 Token 验证的网站数据?
在对文本数据的情感分析中,基于情感词典的方法是最简单也是最常用的一种了。 它的大体思路如下: 对文档分词,找出文档中的情感词、否定词以及程度副词,然后判断每个情感词之前是否有否定词及程度副词,将它之前的否定…

多线程显示运行状态
最近碰见一个例子,Copy大文件或者网络访问的时候处理假死。 那就用多线程加个进度条(只显示运行,没有进度)来表示状态运行吧。好了,废话少说,上个例子。先看结果图: 程序说明: 点击Button,运行…
【Python培训基础知识】单例模式
单例模式是保证一个类仅有一个实例的设计模式。Windows中的任务管理器就是一个典型的单例模式软件。Windows任务管理器如图所示。 Windows任务管理器只能打开一个,即使用户重复打开,也只能获得一个实例,这不同于Word等软件可以打开多个实例。…

Android读写XML(上)
XML 经常用作 Internet 上的一种数据格式,其文件格式想必大家都比较清楚,在这里我结合Android平台,来说明Android SDK提供的读写XML的package。 首先介绍下Android SDK与Java SDK在读写XML文件方面,数据包之间的关系。Android 平台…

Lighttpd1.4.20源代码分析 笔记 状态机之错误处理和连接关闭
这里所说的错误有两种: 1.http协议规定的错误,如404错误。 2.server执行过程中的错误。如write错误。 对于http协议规定的错误,这里的“错误”是针对client的。lighttpd返回相应的错误提示文件之后,相当于顺利的完毕了一次请求&…

资料分享:送你一本《数据结构(C语言版)》电子书!
要想写出可复用、可扩展、易维护、灵活性好的代码,「数据结构」这一关必须要过啊! 在数据结构与算法的众多教材中,奉为经典的当属清华大学严蔚敏老师的著作。很多学校也选择这本书作为考研指定教材。 正在学习数据结构与算法这门课程的同学…

零基础学python培训需要学习多久?
Python是一种入门比较简单的编程语言,但是如果是零基础学员,学习起来还是需要时间的,那么零基础学python培训需要学习多久呢?我们来看看小编的详细介绍吧。 零基础学python培训需要学习多久? 现在的培训机构,一般Python的培训时…

拖动无标题窗体
方法一: 当用户点击窗体的时候欺骗系统,用户是点在标题栏上,这样就完成了无标题栏窗体的拖动,实现如下: 在 MESSAGE_HANDLER(WM_NCHITTEST, OnNcHitTest) 这个函数的方法里 : LRESULT CNyWnd::OnNcHitTest(…

如何利用 C# 爬取Gate.io交易所的公告!
对于大部分程序员来说,都希望自己或多或少拥有一些比特币(BTC)。获取 BTC 的途径除了挖矿计算 Hash 值之外,就是去交易所购买了。 由于 BTC 的价格波动非常剧烈,入手 BTC 的时机就显得尤为关键。在交易所搞活动时入手…

人的原罪、本我和超我
摘自:https://www.zhihu.com/question/31362451/answer/51606300人的原罪的存在,因为人人皆有,所以在潜意识中,形成了对本我的接纳,而神爱世人与宽恕的存在,形成了本我与超我的良性互动。 在这样的关系中&a…
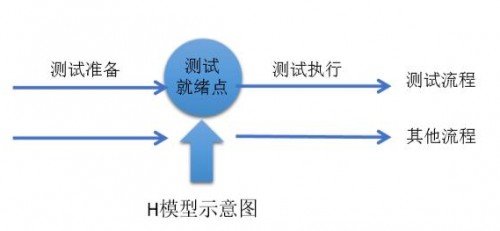
软件测试的准入准出是什么?标准是什么?
测试的准入准出是指什么情况下可以开始当前版本的测试工作,什么情况下可以结束当前版本的测试工作。不同项目、不同公司的测试准入准出标准都会有所不同。下面介绍一些通用的测试准入准出标准。 测试准入标准如下: (1)开发编码结束,开发人员在…

如何利用 C# 爬取 One 持有者返利数据!
去年,10月份写过一篇图文 「One」的投资价值分析,多半年过去了,回头看看当时的判断还是合理的。 投资这种事情需要有自己的策略,更需要理性。任何决策都需要以数据作为判断的基础,哪么是否还继续持有 ONE呢?…

04.微博消息的语言检测
04.微博消息的语言检测 郑昀 201010 隶属于《02.数据解析》小节 大意是,封装Google语言检测ajax web service的接口,输入一段话,输出语言种类。这个方法是从RssMeme.com看来的,经测试效果还不错,可用于检测微博客消息的…

CIO时代学院院长姚乐:传统行业遇上大数据 拥抱智能化未来
近几年,互联网行业发展突飞猛进,“大数据”技术瞬间变得炙手可热,当然,对于发展中的大数据技术而言,很多行业都不会错失良机。近日,CIO时代学院院长、中国新一代IT产业推进联盟秘书长姚乐在“2016CIO时代中…

自动化测试的优势和局限性有哪些
自动化测试只是众多测试中的一种,并不比人工测试更高级更先进。和人工测试相比自动化测试有一定的优势和劣势,具体如下。 1.优势 (1)自动化测试具有一致性和重复性的特点,而且测试更客观,提高了软件测试的准确度、精确度和可信任度…
