技术图文:位运算技术在求解算法题中的应用
背景
前段时间,在知识星球立了一个Flag,这是总结Leetcode刷题的第一篇图文。

在总结这篇图文的时候,顺便把遇到的坑写了两篇辅助的图文,大家可以参考一下:
- 有符号整型的数据范围为什么负数比正数多一个?
- Python 位运算防坑指南
理论部分
1. 原码、反码和补码
二进制有三种不同的表示形式:原码、反码和补码,计算机内部使用补码来表示。
原码:就是其二进制表示(注意,有一位符号位)。
00 00 00 11 -> 3
10 00 00 11 -> -3
反码:正数的反码就是原码,负数的反码是符号位不变,其余位取反(对应正数按位取反)。
00 00 00 11 -> 3
11 11 11 00 -> -3
补码:正数的补码就是原码,负数的补码是反码+1。
00 00 00 11 -> 3
11 11 11 01 -> -3
符号位:最高位为符号位,0表示正数,1表示负数。在位运算中符号位也参与运算。
2. 按位非操作 ~
~ 1 = 0
~ 0 = 1
~ 把num的补码中的 0 和 1 全部取反(0 变为 1,1 变为 0)有符号整数的符号位在 ~ 运算中同样会取反。
00 00 01 01 -> 5
~
---
11 11 10 10 -> -611 11 10 11 -> -5
~
---
00 00 01 00 -> 4
3. 按位与操作 &
1 & 1 = 1
1 & 0 = 0
0 & 1 = 0
0 & 0 = 0
只有两个对应位都为 1 时才为 1
00 00 01 01 -> 5
&
00 00 01 10 -> 6
---
00 00 01 00 -> 4
4. 按位或操作 |
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0
只要两个对应位中有一个 1 时就为 1
00 00 01 01 -> 5
|
00 00 01 10 -> 6
---
00 00 01 11 -> 7
5. 按位异或操作 ^
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0
只有两个对应位不同时才为 1
00 00 01 01 -> 5
^
00 00 01 10 -> 6
---
00 00 00 11 -> 3
异或操作的性质:满足交换律和结合律
A: 00 00 11 00
B: 00 00 01 11A^B: 00 00 10 11
B^A: 00 00 10 11A^A: 00 00 00 00
A^0: 00 00 11 00A^B^A: = A^A^B = B = 00 00 01 11
6. 按位左移操作 <<
num << i 将num的二进制表示向左移动i位所得的值。
00 00 10 11 -> 11
11 << 3
---
01 01 10 00 -> 88
7. 按位右移操作 >>
num >> i 将num的二进制表示向右移动i位所得的值。
00 00 10 11 -> 11
11 >> 2
---
00 00 00 10 -> 2
8. 利用位运算实现快速计算
通过 <<,>> 快速计算2的倍数问题。
n << 1 -> 计算 n*2
n >> 1 -> 计算 n/2,负奇数的运算不可用
n << m -> 计算 n*(2^m),即乘以 2 的 m 次方
n >> m -> 计算 n/(2^m),即除以 2 的 m 次方
1 << n -> 2^n
通过 ^ 快速交换两个整数。
a ^= b
b ^= a
a ^= b
通过 a & (-a) 快速获取a的最后为 1 位置的整数。
00 00 01 01 -> 5
&
11 11 10 11 -> -5
---
00 00 00 01 -> 100 00 11 10 -> 14
&
11 11 00 10 -> -14
---
00 00 00 10 -> 2
9. 利用位运算实现整数集合
一个数的二进制表示可以看作是一个集合(0 表示不在集合中,1 表示在集合中)。
比如集合 {1, 3, 4, 8},可以表示成 01 00 01 10 10 而对应的位运算也就可以看作是对集合进行的操作。
元素与集合的操作:
a | (1<<i) -> 把 i 插入到集合中
a & ~(1<<i) -> 把 i 从集合中删除
a & (1<<i) -> 判断 i 是否属于该集合(零不属于,非零属于)
集合之间的操作:
a 补 -> ~a
a 交 b -> a & b
a 并 b -> a | b
a 差 b -> a & (~b)
应用部分
题目1:只出现一次的数字
- 题号:136
- 难度:简单
- https://leetcode-cn.com/problems/single-number/
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
思路: 利用"异或"操作的性质。
A: 00 00 11 00
B: 00 00 01 11A^A: 00 00 00 00
A^0: 00 00 11 00A^B^A: = A^A^B = B = 00 00 01 11
C# 实现
- 状态:通过
- 16 / 16 个通过测试用例
- 执行用时: 144 ms, 在所有 C# 提交中击败了 91.76% 的用户
- 内存消耗: 25.4 MB, 在所有 C# 提交中击败了 11.39% 的用户
public class Solution
{public int SingleNumber(int[] nums){int result = 0;for (int i = 0; i < nums.Length; i++){result ^= nums[i];}return result;}
}
Python 实现
- 执行结果:通过
- 执行用时:44 ms, 在所有 Python3 提交中击败了 84.17% 的用户
- 内存消耗:15.3 MB, 在所有 Python3 提交中击败了 5.26% 的用户
class Solution:def singleNumber(self, nums: List[int]) -> int:result = 0for item in nums:result ^= itemreturn result
题目2:2的幂
- 题号:231
- 难度:简单
- https://leetcode-cn.com/problems/power-of-two/
给定一个整数,编写一个函数来判断它是否是 2 的幂次方。
示例 1:
输入: 1
输出: true
解释: 2^0 = 1
示例 2:
输入: 16
输出: true
解释: 2^4 = 16
示例 3:
输入: 218
输出: false
思路: 利用"异或"操作的性质。
A: 00 00 11 00A^A: 00 00 00 00
C# 语言
- 状态:通过
- 1108 / 1108 个通过测试用例
- 执行用时: 36 ms, 在所有 C# 提交中击败了 100.00% 的用户
- 内存消耗: 14.7 MB, 在所有 C# 提交中击败了 100.00% 的用户
public class Solution
{public bool IsPowerOfTwo(int n){if (n < 0)return false;for (int i = 0; i < 32; i++){int mask = 1 << i;if ((n ^ mask) == 0)return true;}return false;}
}
Python 语言
- 执行结果:通过
- 执行用时:44 ms, 在所有 Python3 提交中击败了 51.91% 的用户
- 内存消耗:13.6 MB, 在所有 Python3 提交中击败了 6.25% 的用户
class Solution:def isPowerOfTwo(self, n: int) -> bool:for i in range(32):mask = 1 << iif n ^ mask == 0:return Truereturn False
题目3:只出现一次的数字 III
- 题号:260
- 难度:中等
- https://leetcode-cn.com/problems/single-number-iii/
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。找出只出现一次的那两个元素。
示例 :
输入: [1,2,1,3,2,5]
输出: [3,5]
注意:
- 结果输出的顺序并不重要,对于上面的例子, [5, 3] 也是正确答案。
- 你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
思路: 利用"异或"操作的性质。
通过异或操作 ^ 去除掉恰好重复出现两次的元素,这时得到两个只出现一次整数的异或结果different。
A: 00 00 11 00
B: 00 00 01 11A^B: 00 00 10 11
B^A: 00 00 10 11A^A: 00 00 00 00
A^0: 00 00 11 00A^B^A: = A^A^B = B = 00 00 01 11
获取different二进制中最后一位1,通过该位,可以把这两个数分离出来,这两个数在该位是不同的。也即通过该位把 nums 分成了两组,该位是 1 的一组,该位是 0 的一组,然后求两组中只出现一次的整数。
通过 a & (-a) 快速获取a的最后为 1 位置的整数。
00 00 01 01 -> 5
&
11 11 10 11 -> -5
---
00 00 00 01 -> 100 00 11 10 -> 14
&
11 11 00 10 -> -14
---
00 00 00 10 -> 2
C# 语言
- 执行结果:通过
- 执行用时:280 ms, 在所有 C# 提交中击败了 83.33% 的用户
- 内存消耗:31.2 MB, 在所有 C# 提交中击败了 100.00% 的用户
public class Solution
{public int[] SingleNumber(int[] nums){if (nums.Length < 2)return new int[2];int different = 0;for (int i = 0; i < nums.Length; i++){different ^= nums[i];}different &= -1 * different;int num1 = 0, num2 = 0;for (int i = 0; i < nums.Length; i++){if ((different & nums[i]) == 0){num1 ^= nums[i];}else{num2 ^= nums[i];}}return new int[] { num1, num2 };}
}
Python 语言
- 执行结果:通过
- 执行用时:44 ms, 在所有 Python3 提交中击败了 83.70% 的用户
- 内存消耗:14.8 MB, 在所有 Python3 提交中击败了 33.33% 的用户
class Solution:def singleNumber(self, nums: List[int]) -> List[int]:if len(nums) < 2:return []different = 0for num in nums:different ^= numdifferent &= -1 * differentnum1, num2 = 0, 0for num in nums:if (num & different) == 0:num1 ^= numelse:num2 ^= numreturn [num1, num2]
题目4:子集
- 题号:78
- 难度:中等
- https://leetcode-cn.com/problems/subsets/
给定一组 不含重复元素 的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]
]
思路: 利用整数集合的思路。
以{1,2,3}为例,三个数,共2^3个子集。
000 -> []
100 -> [1]
101 -> [1,3]
110 -> [1,2]
111 -> [1,2,3]
...
C# 语言
- 状态:通过
- 10 / 10 个通过测试用例
- 执行用时: 348 ms, 在所有 C# 提交中击败了 97.80% 的用户
- 内存消耗: 29.5 MB, 在所有 C# 提交中击败了 6.67% 的用户
public class Solution
{public IList<IList<int>> Subsets(int[] nums){IList<IList<int>> result = new List<IList<int>>();int count = nums.Length;for (int i = 0; i < 1 << count; i++){IList<int> item = new List<int>();for (int j = 0; j < count; j++){int mask = 1 << j;if ((mask & i) != 0)item.Add(nums[j]);}result.Add(item);}return result;}
}
Python 语言
- 执行结果:通过
- 执行用时:40 ms, 在所有 Python3 提交中击败了 63.08% 的用户
- 内存消耗:13.8 MB, 在所有 Python3 提交中击败了 5.72% 的用户
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:count = len(nums)result = []for i in range(1 << count):item = []for j in range(count):mask = 1 << jif (mask & i) != 0:item.append(nums[j])result.append(item)return result
题目5:Pow(x, n)
- 题号:50
- 难度:中等
- https://leetcode-cn.com/problems/powx-n/
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
示例 4:
输入: 1.00000, -2147483648
输出: 1.00000
说明:
- -100.0 < x < 100.0
- n 是 32 位有符号整数,其数值范围是 [−2^31, 2^31 − 1] 。
思路:利用快速幂法。
假设我们要求a^b,那么b可以拆成二进制表示,例如当b = 5时,5的二进制是0101,5 = 2^3×0 + 2^2×1 + 2^1×0 + 2^0×1,因此,我们将a^5转化为算 a^(2^3×0 + 2^2×1 + 2^1×0 + 2^0×1),即a^(2^0) × a^(2^2)。

我们先算出所有2的幂,然后在算出所有x的2的幂次方。再把n拆成二进制,把二进制当中对应位置是1的值乘起来,就得到了结果。这套方法称为 快速幂法。
C# 实现
- 执行结果:通过
- 执行用时:56 ms, 在所有 C# 提交中击败了 51.87% 的用户
- 内存消耗:15.1 MB, 在所有 C# 提交中击败了 50.00% 的用户
public class Solution
{public double MyPow(double x, int n){int neg = n < 0 ? -1 : 1;long g = Math.Abs((long)n);double[] d = new double[32];d[0] = x;for (int i = 1; i < 32; i++){d[i] = d[i - 1] * d[i - 1];}double result = 1.0d;for (int i = 0; i < 32; i++){int mask = 1 << i;if ((mask & g) != 0){result *= d[i];}}return neg != -1 ? result : 1.0 / result;}
}
注意:long g = Math.Abs((long)n);需要把n转换成long,因为Math.Abs(int.MinValue)会产生溢出错误。
Python 实现
- 执行结果:通过
- 执行用时:36 ms, 在所有 Python3 提交中击败了 75.02% 的用户
- 内存消耗:13.8 MB, 在所有 Python3 提交中击败了 8.33% 的用户
class Solution:def myPow(self, x: float, n: int) -> float:neg = -1 if n < 0 else 1n = abs(n)d = list()d.append(x)for i in range(1, 32):d.append(d[-1] * d[-1])result = 1.0for i in range(32):mask = 1 << iif (mask & n) != 0:result *= d[i]return result if neg != -1 else 1.0 / result
题目6:只出现一次的数字 II
- 题号:137
- 难度:中等
- https://leetcode-cn.com/problems/single-number-ii/
给定一个 非空 整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,3,2]
输出: 3
示例 2:
输入: [0,1,0,1,0,1,99]
输出: 99
思路:
初始result = 0,将每个数想象成 32 位的二进制,对于每一位的二进制的1累加起来必然是3N或者3N + 1(出现3次和1次);3N代表目标值在这一位没贡献,3N + 1代表目标值在这一位有贡献(=1),然后将所有有贡献的位记录到result中。这样做的好处是如果题目改成k个一样,只需要把代码改成count % k即可,很通用并列去找每一位。
C# 语言
- 执行结果:通过
- 执行用时:112 ms, 在所有 C# 提交中击败了 91.53% 的用户
- 内存消耗:25.2 MB, 在所有 C# 提交中击败了 100.00% 的用户
public class Solution
{public int SingleNumber(int[] nums){int result = 0;for (int i = 0; i < 32; i++){int mask = 1 << i;int count = 0;for (int j = 0; j < nums.Length; j++){if ((nums[j] & mask) != 0){count++; }}if (count % 3 != 0){result |= mask;}}return result;}
}
Python 语言
class Solution:def singleNumber(self, nums: List[int]) -> int:result = 0for i in range(32):mask = 1 << icount = 0for num in nums:if num & mask != 0:count += 1if count % 3 != 0:result |= maskreturn result
以上 Python 代码与 C# 代码逻辑完全一致,但提交时报错,错误信息如下:
输入:[-2,-2,1,1,-3,1,-3,-3,-4,-2]
输出:4294967292
预期结果:-4
我们发现:
-4 补码为 1111 1111 1111 1111 1111 1111 1111 1100
如果不考虑符号位
1111 1111 1111 1111 1111 1111 1111 1100 -> 4294967292
是不是很坑,C++,C#,Java等语言的整型是限制长度的,如:byte 8位,int 32位,long 64位,但 Python 的整型是不限制长度的(即不存在高位溢出),所以,当输出是负数的时候,会导致认为是正数!因为它把32位有符号整型认为成了无符号整型,真是坑。
我们对以上的代码进行修改,加入判断条件 if result > 2 ** 31-1: 超过32位整型的范围就表示负数了result -= 2 ** 32,即可得到对应的负数。
- 执行结果:通过
- 执行用时:96 ms, 在所有 Python3 提交中击败了 19.00% 的用户
- 内存消耗:14.8 MB, 在所有 Python3 提交中击败了 25.00% 的用户
class Solution:def singleNumber(self, nums: List[int]) -> int:result = 0for i in range(32):mask = 1 << icount = 0for num in nums:if num & mask != 0:count += 1if count % 3 != 0:result |= maskif result > 2 ** 31-1:result -= 2 ** 32return result
题目7:格雷编码
- 题号:89
- 难度:中等
- https://leetcode-cn.com/problems/gray-code/
格雷编码是一个二进制数字系统,在该系统中,两个连续的数值仅有一个位数的差异。
给定一个代表编码总位数的非负整数 n,打印其格雷编码序列。格雷编码序列必须以 0 开头。
示例 1:
输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2对于给定的 n,其格雷编码序列并不唯一。
例如,[0,2,3,1] 也是一个有效的格雷编码序列。00 - 0
10 - 2
11 - 3
01 - 1
示例 2:
输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。给定编码总位数为 n 的格雷编码序列,其长度为 2^n。当 n = 0 时,长度为 2^0 = 1。因此,当 n = 0 时,其格雷编码序列为 [0]。
思路:
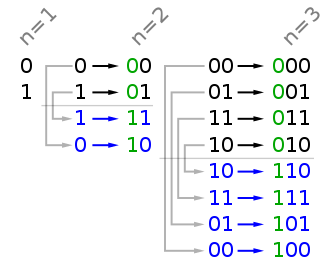
由 n 位推导 n+1 位结果时,n+1 位结果包含 n 位结果,同时包含 n 位结果中在高位再增加一个位 1 所形成的令一半结果,但是这一半结果需要与前一半结果镜像排列。
C# 语言
- 状态:通过
- 12 / 12 个通过测试用例
- 执行用时: 296 ms, 在所有 C# 提交中击败了 95.83% 的用户
- 内存消耗: 24.8 MB, 在所有 C# 提交中击败了 16.67% 的用户
public class Solution
{public IList<int> GrayCode(int n){IList<int> lst = new List<int>();lst.Add(0);for (int i = 1; i <= n; i++){for (int j = lst.Count - 1; j >= 0; j--){int item = lst[j] + (1 << i - 1);lst.Add(item);}}return lst;}
}
Python 语言
- 执行结果:通过
- 执行用时:44 ms, 在所有 Python3 提交中击败了 45.92% 的用户
- 内存消耗:13.8 MB, 在所有 Python3 提交中击败了 20.00% 的用户
class Solution:def grayCode(self, n: int) -> List[int]:lst = [0]for i in range(1, n + 1):count = len(lst)for j in range(count - 1, -1, -1):lst.append(lst[j] + (1 << i - 1))return lst
注意:运算符的优先级
- 一元运算符优于二元运算符。如正负号。
- 先算术运算,后移位运算,最后位运算。例如 1 << 3 + 2 & 7等价于 (1 << (3 + 2)) & 7
- 逻辑运算最后结合
总结
这篇图文总结了位运算技术并通过7道 Leetcode 题目演示了这些理论的具体应用。目前该 Flag 计划已经完成20%,要努力,要努力,千万不要陷入“习得性无助”的陷阱中。今天就到这里吧!See You!
参考文献
- https://oi-wiki.org/math/bit/
- https://www.zhihu.com/question/314455297
- https://mp.weixin.qq.com/s/c5Lf4cNT3i8CHT_tEPfQUw
- https://mp.weixin.qq.com/s/8aG4XwSxjMLG0TIbX_hBBQ
往期活动
LSGO软件技术团队会定期开展提升编程技能的刻意练习活动,希望大家能够参与进来一起刻意练习,一起学习进步!
- Python基础刻意练习活动即将开启,你参加吗?
- Task01:变量、运算符与数据类型
- Task02:条件与循环
- Task03:列表与元组
- Task04:字符串与序列
- Task05:函数与Lambda表达式
- Task06:字典与集合
- Task07:文件与文件系统
- Task08:异常处理
- Task09:else 与 with 语句
- Task10:类与对象
- Task11:魔法方法
- Task12:模块
我是 终身学习者“老马”,一个长期践行“结伴式学习”理念的 中年大叔。
我崇尚分享,渴望成长,于2010年创立了“LSGO软件技术团队”,并加入了国内著名的开源组织“Datawhale”,也是“Dre@mtech”、“智能机器人研究中心”和“大数据与哲学社会科学实验室”的一员。
愿我们一起学习,一起进步,相互陪伴,共同成长。
后台回复「搜搜搜」,随机获取电子资源!
欢迎关注,请扫描二维码:

相关文章:

JavaScript学习系列6 充实文档的内容
JavaScript 两项基本原则渐进增强:你应该总是从最核心的部分,也就是从内容开始。应该根据内容使用标记实现良好的结构;然后再逐步加强这些内容。平稳退化:不支持JavaScript也能访问基本内容。内容:我们在Html文件中编辑…

mapreduce中设置自定义的输入类,进行文本解析(默认以tab键为分隔符)
job.setInputFormatClass(KeyValueTextInputFormat.class);//此时map端输入的键的内容为第一个tab键以左的内容,值得内容为第一个tab键以右的内容转载于:https://www.cnblogs.com/le-ping/p/7788973.html

如何分辨Web前端培训机构的好坏
web前端在互联网行业有着非常高的薪水和很好的前景,想要学习web前端的人越来越多,对于web前端培训机构的选择让很多人犯了难,那么如何分辨Web前端培训机构的好坏呢?该如何选择呢?来看看下面的详细介绍。 如何分辨Web前端培训机构的好坏? 1…

mysql dba系统学习(19)配置mysql+lvs+keeplived实现Mysql读操作的负载均衡
配置mysqllvskeeplived实现Mysql读操作的负载均衡 环境: test1192.168.46.131master test2192.168.46.130slave备份test库 test3调度器 1、安装与配置Keepalived 首先在节点test1、test2上安装Keepalived软件,软件安装非常简单。 12345678910111213[root…
技术图文:浅析 C# Dictionary实现原理
背景 对于 C# 中的 Dictionary类 相信大家都不陌生,这是一个 Collection(集合) 类型,可以通过 Key/Value (键值对) 的形式来存放数据;该类最大的优点就是它查找元素的时间复杂度接近 O(1),实际项目中常被用来做一些数据的本地缓存…

思念水饺吃成泡沫水饺(图)思念质量门
思念再曝水饺吃出泡沫 !思念带着“创可贴汤圆”和“泡沫水饺”“拜晚年”了,而失去新国标的“护身符”,思念这次还要找出什么样的借口为汤圆里的创可贴和水饺里的泡沫找“台阶”下呢?思念汤圆刚被爆吃出创可贴,思念水饺…
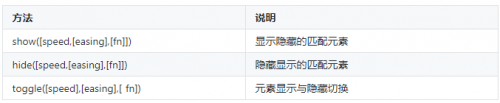
jQuery动画的显示与隐藏效果
jQuery中用于控制元素显示和隐藏效果的方法如表1所示。 表1 控制元素的显示和隐藏 在表1中,参数speed表示动画的速度,可设置为动画时长的毫秒值(如1000),或预定的3种速度(slow、fast和normal);参数easing表示切换效果,默认效果为s…

技术图文:字典技术在求解算法题中的应用
背景 前段时间,在知识星球立了一个Flag,这是总结Leetcode刷题的第二篇图文。 在总结这篇图文的时候,顺便总结了 C# 中Dictionary类的实现,大家可以参考一下: 浅析 C# Dictionary实现原理 理论部分 C# 中字典的常…

[WCF REST] 解决资源并发修改的一个有效的手段:条件更新(Conditional Update)
条件获取(Conditional Update)可以避免相同数据的重复传输,进而提高性能。条件更新(Conditional Update)用于解决资源并发操作问题。如果我们预先获取一个资源进行修改或者删除,条件更新检验帮助我们确认资…

Netty 之 Zero-copy 的实现(下)
上一篇说到了 CompositeByteBuf ,这一篇接着上篇的讲下去。 FileRegion 让我们先看一个Netty官方的example // netty-netty-4.1.16.Final\example\src\main\java\io\netty\example\file\FileServerHandler.java public void channelRead0(ChannelHandlerContext ctx…

Java中final关键字如何使用?
final变量只能赋值一次,赋值的方式有三种: 1)声明变量时直接赋值; 2)非静态成员变量在{}块中赋值,静态成员变量在static{}块中赋值; 3)非静态成员变量在构造方法中赋值。 final修饰类 final类不能被继承,因此不会有子类。final类中…

技术图文:双指针在求解算法题中的应用
背景 前段时间,在知识星球立了一个Flag,这是总结Leetcode刷题的第三篇图文。 理论部分 Python list 的源码地址: https://github.com/python/cpython/blob/master/Include/listobject.h https://github.com/python/cpython/blob/master/O…

【CSON原创】HTML5游戏框架cnGameJS开发实录(外部输入模块篇)
返回目录 1.为什么我们需要外部输入模块? 在游戏中我们常常用到类似这样的操作:鼠标点击某位置,玩家对象移动到该位置,或者按鼠标方向键,玩家向不同方向移动,等等。这些操作无一不用与外部输入设备打交道。…

中国科协(深圳)海外人才离岸创新创业基地源创力中心开业,主打国际创业服务...
2017年9月28日,由深圳市科学技术协会主办、深圳市罗湖区人民政府支持,深圳市源创力离岸创新中心承办的“梧桐山基地开园仪式暨梧桐湾未来论坛”于深圳举办。 据介绍, “中国科协(深圳)海外人才离岸创新创业基地”是在深…

找java培训机构如何挑选
java技术在互联网行业的需求率还是非常高的,它的发展前景非常可观,想要学好java技术,那么寻找一个好的java培训机构是非常重要的,那么找java培训机构如何挑选呢?来看看下面的详细介绍。 找java培训机构如何挑选? 在选择…

技术图文:集合技术在求解算法题中的应用
背景 前段时间,在知识星球立了一个Flag,这是总结Leetcode刷题的第四篇图文。 理论部分 HashSet C# 语言中 HashSet<T> 是包含不重复项的无序列表,称为“集合(set)”。由于set是一个保留字,所以用HashSet来表示。 public…

sql server 2008数据导入Oracle方法
试了几种sql server数据导入Oracle的方法,发现还是sql server 的导入导出工具最好使。使用方法很简单,照着向导做就可以。不过使用中需要注意以下几点: 系统盘需要足够大。因为SSIS的临时文件都是生成在系统盘的,系统盘太小&#…
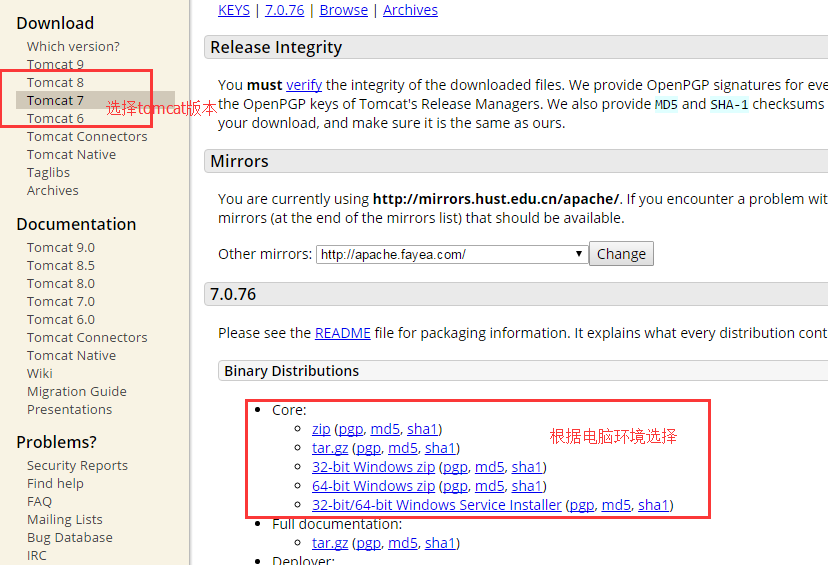
nginx+tomcat配置负载均衡集群
一、Hello world 1、前期环境准备 准备两个解压版tomcat,如何同时启动两个tomcat,方法如下: 首先去apache tomcat官网下载一个tomcat解压版。 解压该压缩包,生成n份tomcat 分别命名为 tomcat1,tomcat2, 然后…

参加UI设计培训要学多久
UI设计要学习的内容有很多,至于参加UI设计培训要学多久这个问题,要看你的学习能力和所在的UI设计培训机构都教些什么,我们来看看下面的详细介绍。 参加UI设计培训要学多久?千锋教育的课程大纲分享给大家参考学习一下: 阶段一&…

技术图文:C# 语言中的扩展方法
背景 前段时间,在知识星球立了一个Flag,在总结 Leetcode 刷题的第五篇图文时遇到了扩展方法 这个知识点,于是先总结一下。 1.扩展方法概述 扩展方法能够向现有类型“添加”方法,而无需创建新的派生类型、重新编译或以…

如何在ToolBar中显示文字和图标,自定义图标大小,并和MenuItem关联
要注意以下几个方面,先后顺序未必正确,有可能多设几次 1.设置ToolBar可以显示文字ToolBar.ShowCaption : True;2.设置ToolButton大小ImageList.WidthImageList.Height3.设置菜单关联4.设置运行时显示图标(这个是关键)ToolButton.Menuitum.ImageIndex要保证MenuItem所在的MainMe…

C#程序调用cmd执行命令
酷小孩 原文 C#程序调用cmd执行命令 对于C#通过程序来调用cmd命令的操作,网上有很多类似的文章,但很多都不行,竟是漫天的拷贝。我自己测试整理了一下。 代码: string str Console.ReadLine();System.Diagnostics.Process p new …
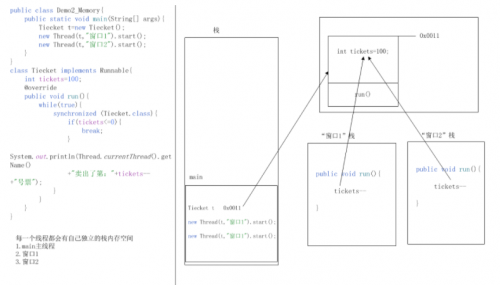
Java虚拟机的内存空间有几种
Java虚拟机的内存空间有几种?(1)问题分析: JVM(虚拟机)的内存划分 不同的数据使用的是哪一块内存空间 (2)核心答案讲解: Java虚拟机有那几块内存空间: 1)栈内存:方法运行时所进入的内存,里面还会存储程序的…

技术图文:排序技术在求解算法题中的应用
背景 前段时间,在知识星球立了一个Flag,这是总结Leetcode刷题的第五篇图文。 理论部分 C# 中的排序 对集合类的排序,我们通常使用位于 System.Core 程序集,System.Linq命名空间下,Enumerable静态类中的扩展方法。 …

如果有电脑——计算机达人成长之路(36)
5、电脑情缘(一)王新华的电脑 现在的大学生一般都有一个工具,就是计算机,尤其是计算机科学系的学生,几乎人手一台。对此,木鸿飞只能深深的说上一句:“幸福啊!” 现在人可能不能了解这…

Javascript中二进制数据处理方法
Javascript中二进制数据处理方法 转载于:https://www.cnblogs.com/motadou/archive/2012/02/19/2358514.html

正规Java培训机构是什么样的
正规Java培训机构是什么样的?这对于很多想真正学习到java技术的人来说是非常重要的,选择一个适合自己的靠谱的Java培训机构,学有所成工作也是比较稳定的,下面我们来看看详细的介绍。 正规Java培训机构是什么样的?其实对于这个问题…

《40期》 我们要把世纪末日变成重生日
2012年.传说中一个会是世纪末日的一年。(ps:电影看多了……- _-!!!),但是寒假过后的北京。天气却是十分的晴朗、出奇的好。而就在今天也就是2012年2月9日40期的开班典礼就选了这一天。地点就是在育荣教学园区2栋教学楼…

LeetCode刷题宝典 V1.0 PDF下载
前段时间,在知识星球立了一个Flag,现在 Flag 的进度为 100%,很是开心。 为了大家学习的方便,所以整理了这份150多页的小册子。可以作为学习数据结构与算法或备考计算机类研究生的参考资料,希望对大家有所帮助。 小册子…

机器学习:信用风险评估评分卡建模方法及原理
#课程介绍 信用风险评分卡为信用风险管理提供了一种有效的、经验性的解决方法,是消费信贷管理中广泛应用的技术手段。 评分卡是信用风险评估领域常见的建模方法。评分卡并不加单对应于某一种机器学习算法,而是一种通用的建模框架,讲原始数据通…
