数据结构与算法:09 栈与递归
09 栈与递归
知识结构:
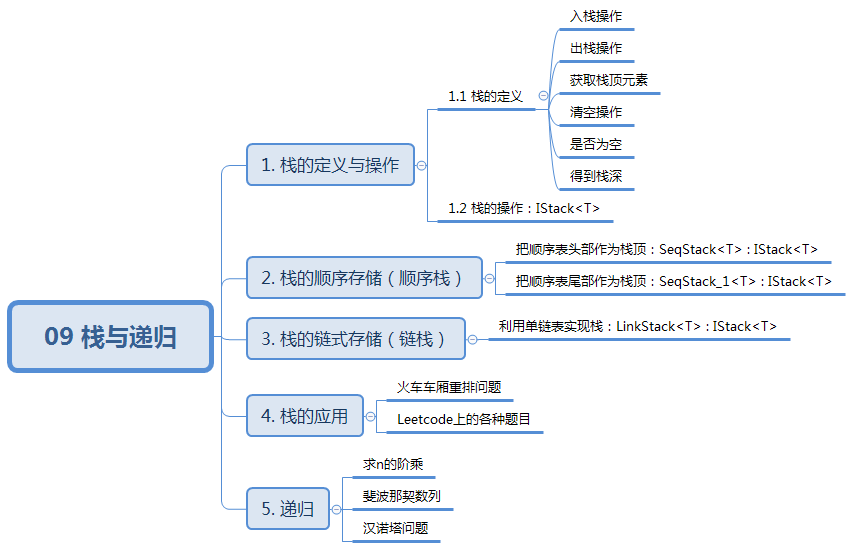
栈是我们经常使用的一种数据结构,比如,手枪发射子弹的顺序与子弹压入弹夹的顺序是相反,即后压入弹夹的子弹先发射出来。又比如,我们使用的Word、Excel、Photoshop等软件系统中的撤销操作,也是栈的具体应用,最后做的操作,一定是最先撤销的。
下面我们就来详细介绍“栈”这种数据结构。
1. 栈的定义与操作
1.1 栈的定义
插入(入栈)和删除(出栈)操作只能在一端(栈顶)进行的线性表。即先进后出(First In Last Out)的线性表。
例1 :线性表$(a_0,a_1,⋯,a_{n-1)}$进栈与出栈演示。
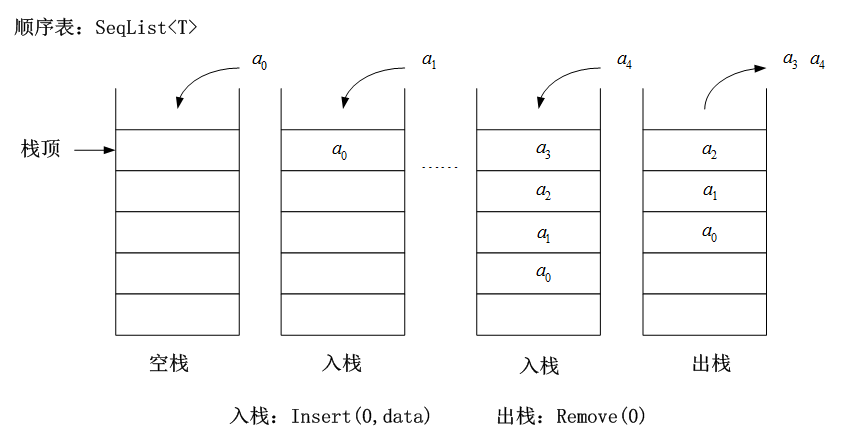
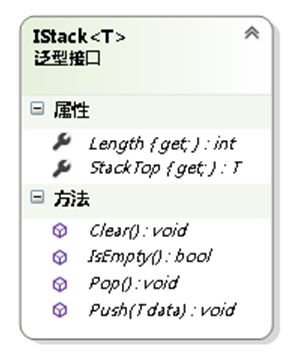
1.2 栈的操作
- 入栈操作:将数据元素插入栈顶。
- 出栈操作:移除栈顶的数据元素。
- 是否为空:判断栈中是否包含数据元素。
- 得到栈深:获取栈中实际包含数据元素的个数。
- 清空操作:移除栈中的所有数据元素。
- 获取栈顶元素。
using System;namespace LinearStruct
{/// <summary>/// 栈的抽象数据类型/// </summary>/// <typeparam name="T">栈中元素的类型</typeparam>public interface IStack<T> where T : IComparable<T>{/// <summary>/// 获取栈中实际包含元素的个数/// </summary>int Length { get; }/// <summary>/// 获取栈顶元素/// </summary>T StackTop { get; }/// <summary>/// 数据元素入栈/// </summary>/// <param name="data">要入栈的元素</param>void Push(T data);/// <summary>/// 数据元素出栈/// </summary>void Pop();/// <summary>/// 判断栈中是否包含元素/// </summary>/// <returns>如果包含元素返回false,否则返回true.</returns>bool IsEmpty();/// <summary>/// 从栈中移除所有元素/// </summary>void Clear();}
}
2. 栈的顺序存储(顺序栈)
顺序栈:利用顺序表实现的栈。
实现:
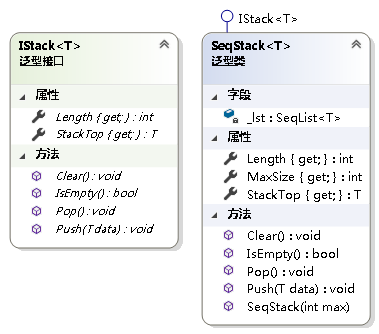
using System;namespace LinearStruct
{/// <summary>/// 用顺序存储结构实现的栈/// </summary>/// <typeparam name="T">顺序栈中元素的类型</typeparam>public class SeqStack<T> : IStack<T> where T : IComparable<T>{private readonly SeqList<T> _lst;/// <summary>/// 初始化SeqStack类的新实例/// </summary>/// <param name="max">SeqStack中最多包含元素的个数</param>public SeqStack(int max){if (max <= 0)throw new ArgumentOutOfRangeException();_lst = new SeqList<T>(max);}/// <summary>/// 获取SeqStack中实际包含元素的个数/// </summary>public int Length{get { return _lst.Length; }}/// <summary>/// 获取SeqStack中最多包含元素的个数/// </summary>public int MaxSize{get { return _lst.MaxSize; }}/// <summary>/// 获取SeqStack中的栈顶元素/// </summary>public T StackTop{get{if (_lst.IsEmpty())throw new Exception("栈为空.");return _lst[0];}}/// <summary>/// 数据元素入栈/// </summary>/// <param name="data">要入栈的元素</param>public void Push(T data){if (_lst.Length == _lst.MaxSize)throw new Exception("栈已达到最大容量.");_lst.Insert(0, data);}/// <summary>/// 数据元素出栈/// </summary>public void Pop(){if (_lst.IsEmpty())throw new Exception("栈为空.");_lst.Remove(0);}/// <summary>/// 判断SeqStack中是否包含元素/// </summary>/// <returns>如果包含元素返回false,否则返回true.</returns>public bool IsEmpty(){return _lst.IsEmpty();}/// <summary>/// 从SeqStack中移除所有元素/// </summary>public void Clear(){_lst.Clear();}}
}
应用:
using System;
using LinearStruct;namespace ExampleStack
{class Program{static void Main(string[] args){StackTest(new SeqStack<string>(20));}private static void StackTest(IStack<string> stack){stack.Push("a1");stack.Push("a2");stack.Push("a3");while (stack.IsEmpty() == false){Console.WriteLine(stack.StackTop);stack.Pop();}// a3// a2// a1}}
}
SeqStack<T>虽然实现了IStack<T>接口,但在入栈和出栈时,会移动大量的元素,效率比较低。故把入栈和出栈放到顺序表的尾部进行,这样可以提升效率。

- 入栈:
Insert(Length, data) - 出栈:
Remove(Length - 1) - 栈顶元素:
SeqList[Length - 1]
using System;namespace LinearStruct
{/// <summary>/// 用顺序存储结构实现的栈/// </summary>/// <typeparam name="T">顺序栈中元素的类型</typeparam>public class SeqStack_1<T> : IStack<T> where T : IComparable<T>{private readonly SeqList<T> _lst;/// <summary>/// 初始化SeqStack类的新实例/// </summary>/// <param name="max">SeqStack中最多包含元素的个数</param>public SeqStack_1(int max){if (max <= 0)throw new ArgumentOutOfRangeException();_lst = new SeqList<T>(max);}/// <summary>/// 获取SeqStack中实际包含元素的个数/// </summary>public int Length{get { return _lst.Length; }}/// <summary>/// 获取SeqStack中最多包含元素的个数/// </summary>public int MaxSize{get { return _lst.MaxSize; }}/// <summary>/// 获取SeqStack中的栈顶元素/// </summary>public T StackTop{get{if (_lst.IsEmpty())throw new Exception("栈为空.");return _lst[Length - 1];}}/// <summary>/// 数据元素入栈/// </summary>/// <param name="data">要入栈的元素</param>public void Push(T data){if (_lst.Length == _lst.MaxSize)throw new Exception("栈已达到最大容量.");_lst.Insert(Length, data);}/// <summary>/// 数据元素出栈/// </summary>public void Pop(){if (_lst.IsEmpty())throw new Exception("栈为空.");_lst.Remove(Length - 1);}/// <summary>/// 判断SeqStack中是否包含元素/// </summary>/// <returns>如果包含元素返回false,否则返回true.</returns>public bool IsEmpty(){return _lst.IsEmpty();}/// <summary>/// 从SeqStack中移除所有元素/// </summary>public void Clear(){_lst.Clear();}}
}
应用:
using System;
using LinearStruct;namespace ExampleStack
{class Program{static void Main(string[] args){StackTest(new SeqStack_1<string>(20));}private static void StackTest(IStack<string> stack){stack.Push("a1");stack.Push("a2");stack.Push("a3");while (stack.IsEmpty() == false){Console.WriteLine(stack.StackTop);stack.Pop();}// a3// a2// a1}}
}
3. 栈的链式存储(链栈)
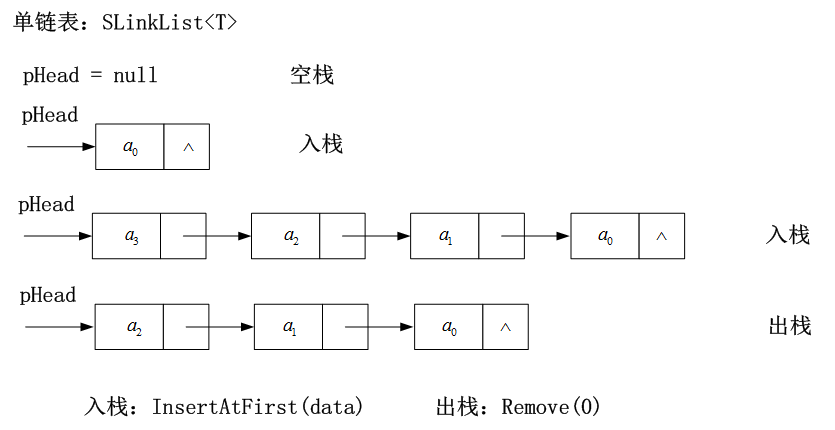
链栈:利用单链表实现的栈。
实现:

using System;namespace LinearStruct
{/// <summary>/// 用链式存储结构实现的栈/// </summary>/// <typeparam name="T">栈中元素的类型</typeparam>public class LinkStack<T> : IStack<T> where T : IComparable<T>{private readonly SLinkList<T> _lst;/// <summary>/// 初始化LinkStack类的新实例/// </summary>public LinkStack(){_lst = new SLinkList<T>();}/// <summary>/// 获取LinkStack中实际包含元素的个数/// </summary>public int Length{get { return _lst.Length; }}/// <summary>/// 获取LinkStack中的栈顶元素/// </summary>public T StackTop{get{if (_lst.Length == 0)throw new Exception("栈为空.");return _lst[0];}}/// <summary>/// 数据元素入栈/// </summary>/// <param name="data">要入栈的元素</param>public void Push(T data){_lst.InsertAtFirst(data);}/// <summary>/// 数据元素出栈/// </summary>public void Pop(){if (_lst.Length == 0)throw new Exception("栈为空.");_lst.Remove(0);}/// <summary>/// 判断LinkStack中是否包含元素/// </summary>/// <returns>如果包含元素返回false,否则返回true.</returns>public bool IsEmpty(){return _lst.IsEmpty();}/// <summary>/// 从LinkStack中移除所有元素/// </summary>public void Clear(){_lst.Clear();}}
}
应用:
using System;
using LinearStruct;namespace ExampleStack
{class Program{static void Main(string[] args){StackTest(new LinkStack<string>());}private static void StackTest(IStack<string> stack){stack.Push("a1");stack.Push("a2");stack.Push("a3");while (stack.IsEmpty() == false){Console.WriteLine(stack.StackTop);stack.Pop();}// a3// a2// a1}}
}
4. 栈的应用
4.1 问题描述
假设一列货运列车共有n节车厢,每节车厢将停放在不同的车站。假定n个车站的编号分别为1至n,货运列车按照第n站至第1站的次序经过这些车站。车厢的编号与它们的目的地相同。为了便于从列车上卸掉相应的车厢,必须重新排列车厢,使各车厢从前至后按编号1至n的次序排列。当所有的车厢都按照这种次序排列时,在每个车站只需卸掉最后一节车厢即可。
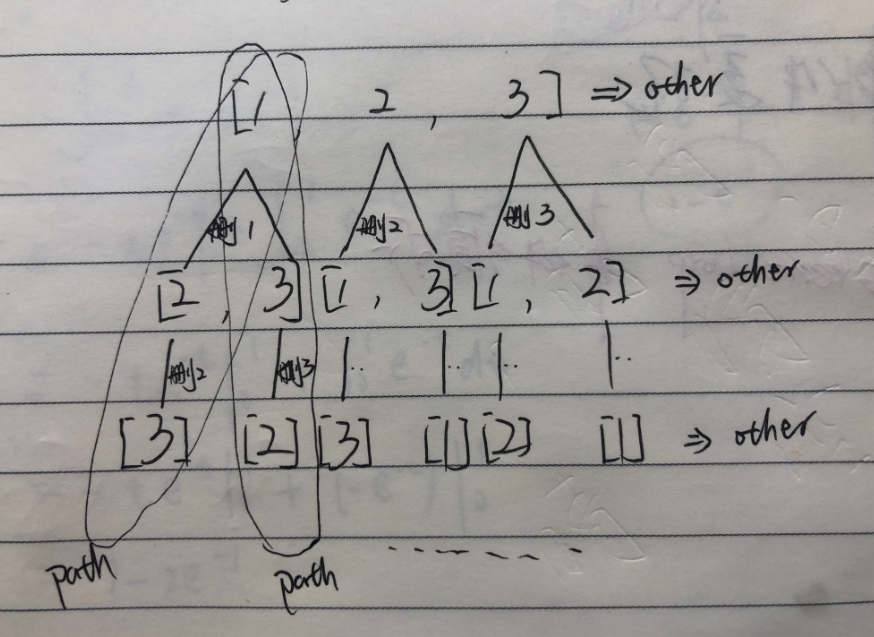
我们在一个转轨站里完成车厢的重排工作,在转轨站中有一个入轨、一个出轨和k个缓冲铁轨(位于入轨和出轨之间)。图1(a)给出一个转轨站,其中有k个(k=3)缓冲铁轨H1,H2和H3。开始时,n节车厢的货车从入轨处进入转轨站,转轨结束时各车厢从右到左按照编号1至n的次序离开转轨站(通过出轨处)。在图1(a)中,n=9,车厢从后至前的初始次序为5,8,1,7,4,2,9,6,3。图1(b)给出了按所要求的次序重新排列后的结果。
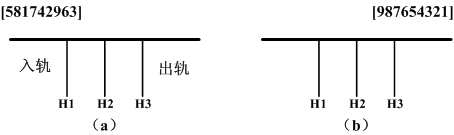
4.2 问题分析
现在分析图1,为了重排车厢,需从前至后依次检查入轨上的所有车厢。如果正在检查的车厢就是下一个满足排列要求的车厢,可以直接把它放到出轨上去。如果不是,则把它移动到缓冲铁轨上,直到按输出次序要求轮到它时才将它放到出轨上。缓冲铁轨上车厢的进和出只能在缓冲铁轨的尾部进行。在重排车厢过程中,仅允许以下移动:
1、车厢可以从入轨移动到一个缓冲铁轨的尾部或进入出轨接在重排的列车后。
2、车厢可以从一个缓冲铁轨的尾部移动到出轨接在重排的列车后。
考察图1(a),3号车厢在入轨的前部,但由于它必须位于1号和2号车厢的后面,因此不能立即输出3号车厢,可把3号车厢送入缓冲铁轨H1。下一节车厢是6号车厢,也必须送入缓冲铁轨。如果把6号车厢送入H1,那么重排过程将无法完成,因为3号车厢位于6号车厢的后面,而按照重排的要求,3号车厢必须在6号车厢之前输出。因此可把6号车厢送入H2。下一节车厢是9号车厢,被送入H3,因为如果把它送入H1或H2,重排过程也将无法完成。至此,缓冲铁轨的当前状态如图2(a)所示。
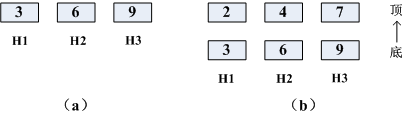
接下来处理2号车厢,它可以被送入任一个缓冲铁轨,因为它能满足缓冲铁轨上车厢编号必须递增排列的要求,不过,应优先把2号车厢送入H1,因为如果把它送入H3,将没有空间来移动7号车厢和8号车厢。如果把2号车厢送入H2,那么接下来的4号车厢必须被送入H3,这样将无法移动后面的5号、7号和8号车厢。新的车厢u应送入这样的缓冲铁轨:其底部的车厢编号v满足v > u,且v是所有满足这种条件的缓冲轨顶部车厢编号中最小的一个编号。只有这样才能使后续的车厢重排所受到的限制最小。
接下来处理4号车厢时,三个缓冲铁轨顶部的车厢分别为2号、6号和9号车厢。根据分配规则,4号车厢应送入H2。这之后,7号车厢被送入H3。图2(b)给出了当前的状态。
接下来,1号车厢被送至出轨,这时,可以把H1中的2号车厢送至出轨。之后,从H1输出3号车厢, 输出4号车厢。至此,没有可以立即输出的车厢了。接下来的8号车厢被送入H1,然后5号车厢从入轨处直接输出到出轨处。这之后,从H2输出6号车厢,从H3输出7号车厢,从H1输出8号车厢,最后从H3输出9号车厢。
到此为止,整个“入轨,出轨”完毕!让我们整理一下算法思路:
- 第一步:若需出轨的编号恰是入轨编号,则直接出轨。
- 第二步:若需出轨的编号恰是缓冲轨的最小编号,则直接出轨。
- 第三步:将入轨编号放入缓冲轨。(规则:放到满足小于缓冲轨栈顶元素编号且栈顶元素最小的上面。)
4.3 参考代码
using System;
using LinearStruct;namespace TrainArrange
{class Program{/// <summary>/// 车厢重排算法/// </summary>/// <param name="p">入轨序列</param>/// <param name="k">缓冲轨条数</param>/// <returns>重排是否成功</returns>static bool RailRoad(int[] p, int k){LinkStack<int>[] h = new LinkStack<int>[k];for (int i = 0; i < h.Length; i++)h[i] = new LinkStack<int>();int nowOut = 1; //下一次要输出的车厢号int minH = int.MaxValue; //缓冲铁轨中编号最小的车厢int minS = -1; //minH号车厢对应的缓冲铁轨for (int i = 0; i < p.Length; i++){if (p[i] == nowOut){Console.WriteLine("移动车厢:{0}从入轨到出轨。", p[i]);nowOut++;//从缓冲铁轨中输出while (minH == nowOut){Output(ref minH, ref minS, h); //出轨nowOut++;}}else{//将p[i]送入某个缓冲铁轨if (Input(p[i], ref minH, ref minS, h) == false){return false;}}}return true;}/// <summary>/// 从缓冲轨移除车厢出轨/// </summary>/// <param name="minH">缓冲铁轨中编号最小的车厢</param>/// <param name="minS">minH号车厢对应的缓冲铁轨</param>/// <param name="h">缓冲轨道的集合</param>static void Output(ref int minH, ref int minS, LinkStack<int>[] h){h[minS].Pop(); //从堆栈minS中删除编号最小的车厢minHConsole.WriteLine("移动车厢:{0}从缓冲轨{1}到出轨。", minH, minS);//通过检查所有的栈顶,搜索新的minH和minSminH = int.MaxValue;minS = -1;for (int i = 0; i < h.Length; i++){if (h[i].IsEmpty() == false && h[i].StackTop < minH){minH = h[i].StackTop;minS = i;}}}/// <summary>/// 在一个缓冲铁轨中放入车厢c/// </summary>/// <param name="c">放入车厢编号</param>/// <param name="minH">栈顶编号的最小值</param>/// <param name="minS">栈顶编号最小值所在堆栈的编号</param>/// <param name="h">缓冲轨道的集合</param>/// <returns>如果没有可用的缓冲铁轨,则返回false,否则返回true。</returns>static bool Input(int c, ref int minH, ref int minS, LinkStack<int>[] h){int bestTrack = -1; //目前最优的铁轨int bestTop = int.MaxValue; //最优铁轨上的头辆车厢for (int i = 0; i < h.Length; i++){if (h[i].IsEmpty() == false){int x = h[i].StackTop;if (c < x && x < bestTop){bestTop = x;bestTrack = i;}}else{if (bestTrack == -1){bestTrack = i;break;}}}if (bestTrack == -1)return false;h[bestTrack].Push(c);Console.WriteLine("移动车厢:{0}从入轨到缓冲轨{1}。", c, bestTrack);if (c < minH){minH = c;minS = bestTrack;}return true;}static void Main(string[] args){int[] p = new int[] { 3, 6, 9, 2, 4, 7, 1, 8, 5 };int k = 3;bool result = RailRoad(p, k);do{if (result == false){Console.WriteLine("需要更多的缓冲轨道,请输入需要添加的数量:");k = k + Convert.ToInt32(Console.ReadLine());result = RailRoad(p, k);}} while (result == false);}}
}
4.4 输出结果
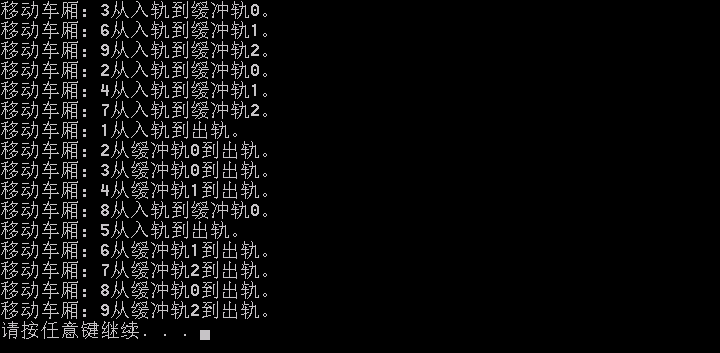
5. 递归
如果一个函数在内部调用自身本身,这个函数就是递归函数。
【例1】:求n的阶乘
n! = 1 x 2 x 3 x ... x n
循环:
static int factorial(int n)
{if (n < 1)throw new ArgumentOutOfRangeException();int result = n;for (int i = 1; i < n; i++){result *= i;}return result;
}static void Main(string[] args)
{Console.WriteLine(factorial(5));//120
}
递归:
static int factorial(int n)
{if (n < 1)throw new ArgumentOutOfRangeException();if (n == 1)return 1;return n * factorial(n - 1);
}static void Main(string[] args)
{Console.WriteLine(factorial(5));//120
}
【例2】:斐波那契数列
f(n)=f(n-1)+f(n-2), f(0)=0 f(1)=1
循环:
static int[] recur_fibo(int n)
{if (n < 2)throw new ArgumentOutOfRangeException();int[] result = new int[n];result[0]= 0;result[1] = 1;for (int i = 2; i < n; i++){result[i] = result[i - 1] + result[i - 2];}return result;
}static void Main(string[] args)
{int[] r = recur_fibo(11);for (int i = 0; i < r.Length; i++){Console.Write(r[i]+" ");}Console.WriteLine();// 0 1 1 2 3 5 8 13 21 34 55
}
递归:
static int recur_fibo(int n)
{if (n <= 1)return n;return recur_fibo(n - 1) + recur_fibo(n - 2);
}static void Main(string[] args)
{int[] result = new int[11];for (int i = 0; i < result.Length; i++){result[i] = recur_fibo(i);Console.Write(result[i] + " ");}Console.WriteLine();// 0 1 1 2 3 5 8 13 21 34 55
}
【例3】:汉诺塔问题
汉诺塔问题源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。

如果我们要思考每一步怎么移可能会非常复杂,但是可以将问题简化。
我们可以先假设除 a 柱最下面的盘子之外,已经成功地将 a 柱上面的 63个盘子移到了 b 柱,这时我们只要再将最下面的盘子由 a 柱移动到 c 柱即可。

当我们将最大的盘子由 a 柱移到 c 柱后,b 柱上便是余下的 63 个盘子,a 柱为空。因此现在的目标就变成了将这 63 个盘子由 b 柱移到 c 柱。这个问题和原来的问题完全一样,只是由 a 柱换为了 b 柱,规模由 64 变为了 63。因此可以采用相同的方法,先将上面的 62 个盘子由 b 柱移到 a 柱,再将最下面的盘子移到 c 柱。
以此内推,再以 b 柱为缓冲,将 a 柱上面的 62 个圆盘最上面的 61 个圆盘移动到 b 柱,并将最后一块圆盘移到 c 柱。
我们已经发现规律,我们每次都是以 a 或 b 中一根柱子为缓冲,然后先将除了最下面的圆盘之外的其它圆盘移动到辅助柱子上,再将最底下的圆盘移到 c 柱子上,不断重复此过程。
这个反复移动圆盘的过程就是递归,例如我们每次想解决 n 个圆盘的移动问题,就要先解决(n-1)个盘子进行同样操作的问题。
于是可以编写一个函数,move(n, a, b, c)。可以这样理解:move(盘子数量, 起点, 缓冲, 终点)。
1. a 上只有一个盘子的情况,直接搬到 c,代码如下:
if(n == 1)Console.WriteLine(a, '-->', c)
2. a 上不止有一个盘子的情况:
首先,需要把 n-1 个盘子搬到 b 柱子缓冲。打印出的效果是:a --> b。
move(n - 1, a, c, b)
再把最大的盘子搬到 c 柱子,也是最大尺寸的一个。打印出:a–>c。
move(1, a, b, c)
最后,把剩下 b 柱的 n-1 个盘子搬到 c 上,此时缓冲变成了起点,起点变成了缓冲。
move(n - 1, b, a, c)
利用 C# 实现汉诺塔问题
class Program
{private static int i = 0;static void Move(int n, string a, string b, string c){if (n == 1){Console.WriteLine("移动第 {0} 次 {1}-->{2}", ++i, a, c);return;}Move(n - 1, a, c, b);Move(1, a, b, c);Move(n - 1, b, a, c);}static void Main(string[] args){Move(3, "a", "b", "c");}
}
// 移动第 1 次 a --> c
// 移动第 2 次 a --> b
// 移动第 3 次 c --> b
// 移动第 4 次 a --> c
// 移动第 5 次 b --> a
// 移动第 6 次 b --> c
// 移动第 7 次 a --> c
后台回复「搜搜搜」,随机获取电子资源!
欢迎关注,请扫描二维码:


相关文章:

Javascript匿名函数
定义 匿名函数的定义非常简单:就是没有名字的函数。但是其用途非常的大 典型的函数定义方式 在看匿名函数之前我们先看下在Javascript中定义一个函数比较典型的几种方式 函数声明 function functionName(args) { //函数体 } 函数表达式 var functionName functi…

零基础学Java大数据难不难
java大数据如今在企业中用到的次数是非常多的,很多人都比较看好java技术,那么零基础学Java大数据难不难?想要学习java技术说难不难,说简单也不是很简单,来看看下面的详细介绍就知道了。 零基础学Java大数据难不难?因人而异&…
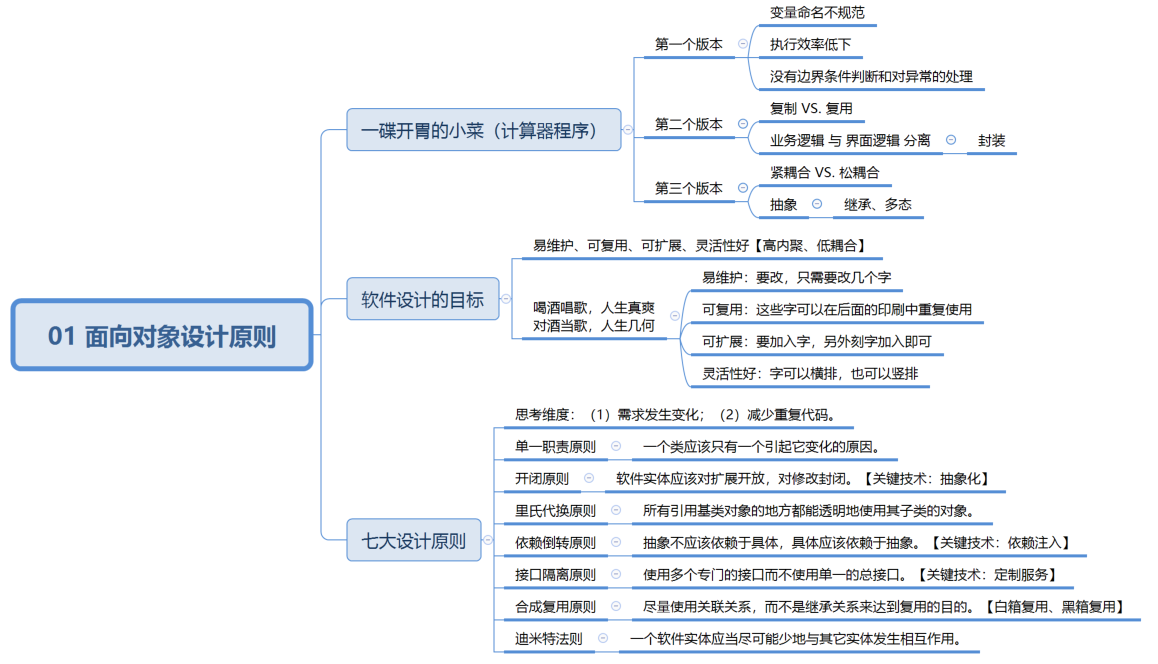
技术图文:01 面向对象设计原则
01 面向对象设计原则 知识结构: 一碟开胃的小菜 小菜今年计算机专业大四了,学了不少软件开发方面的东西,也学着编了些小程序,踌躇满志,一心要找一个好单位。当投递了无数简历后,终于收到了一个单位的面试…

关于GridView手动绑定的一段代码,一切尽在不言中
为GridView绑定主键的方法,在前台的DataGrid标签中加 DataKeyNames"ID" 后台获取ID: int idint.parse(this.GridView.DataKeys[e.RowIndex].Value.Tostring()); 如果DataKeyNames绑定了多个列取法:int idint.parse(this.G…

linux 服务器FTP服务安装教程
1.更新yum源 首先需要更新系统的yum源,便捷工具下载地址:http://help.aliyun.com/manual?spm0.0.0.0.zJ3dBU&helpId1692 2.安装vsftp 使用yum命令安装vsftp #yum install vsftpd -y 3.添加ftp帐号和目录 先检查一下nologin的位置,通常在…

CSS3颜色不透明度如何设置
web前端技术包含HTML和CSS样式,两者是相辅相成的,学习CSS样式不必可少,那么在学习CSS样式中,CSS3颜色不透明度如何设置?在CSS3之前,我们设置颜色的方式包含十六进制颜色(如#F00)、rgb模式颜色、或指定颜色的英文名称(…
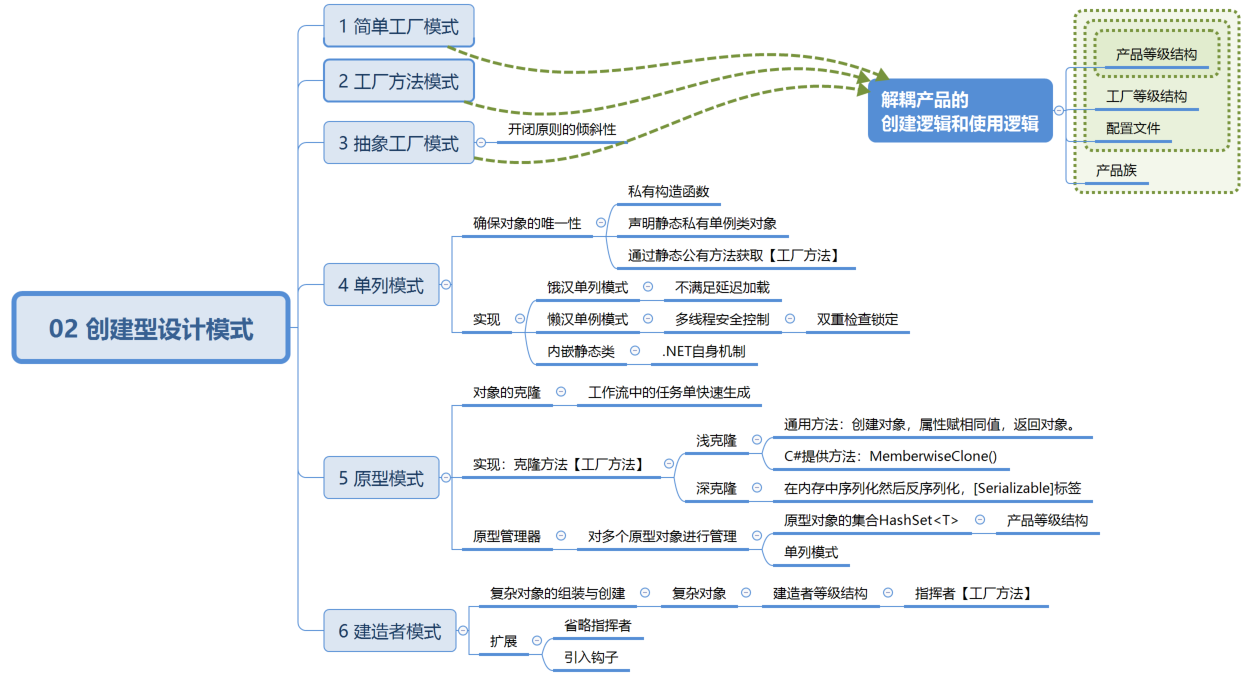
技术图文:02 创建型设计模式(上)
创建型设计模式(上) 知识结构: 图1 知识结构 简单工厂模式 Sunny 软件公司欲基于 C# 语言开发一套图表库,该图表库可以为应用系统提供各种不同外观的图表,如: 柱状图(histogram)饼…

转:初探 jQuery 的 Sizzle 选择器
这是一篇关于介绍jQuery Sizzle选择器的文章,由我和obility共同完成。在文中,我们试图用自己的语言配以适量的代码向读者展现出Sizzle在处理选择符时的流程原理,以及末了以少许文字给你展示出如何借用Sizzle之手实现自定义选择器(…
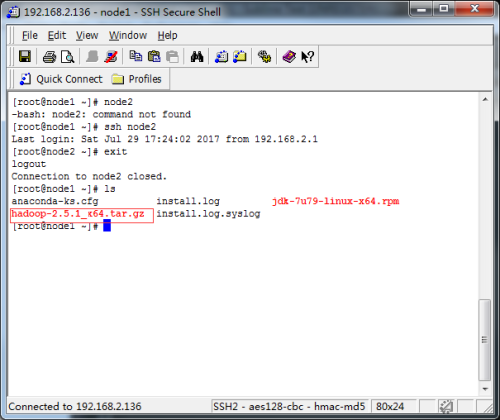
安装hadoop图文
1.下载hadoop-2.5.1,存放根目录 2.通过tar -zxvf 包名 来进行解压 3.通过mv命令将解压后的hadoop包移动到/home下 4.修改hadoop-en.sh配置文件,添加jdk的安装目录,操作如下图所示 5.修改core-site.xml配置文件,添加namenode的配置信息 6.修改hdfs-site.xml配置文件,添加seconda…

Java中父类方法重写有哪些需要注意的?
在继承关系中,子类会自动继承父类中公共的方法,但有时在子类中需要对继承的方法进行一些修改,即对父类的方法进行重写。需要注意的是,子类中重写的方法需要和父类被重写的方法具有相同的方法名、参数列表以及返回值类型。 在上一节…

技术图文:02 创建型设计模式(下)
创建型设计模式(下) 知识结构: 图1 知识结构 单例模式 – 确保对象的唯一性 Sunny 软件公司承接了一个服务器负载均衡软件的开发工作,该软件运行在一台负载均衡服务器上,可以将并发访问和数据流量分发到服务器集群中…

[转载]C# 二进制与十进制,十进制与十六进制相互转换
原文地址:C# 二进制与十进制,十进制与十六进制相互转换作者:tonytonglx十进制转二进制:用2辗转相除至结果为1 将余数和最后的1从下向上倒序写就是结果例如302302/2 151 余0151/2 75 余175/2 37 余137/2 18 余118/2 9 余09/2 4 余14/2 …

感知哈希算法——找出相似的图片
参考Neal Krawetz博士的这篇文章, 实现这种功能的关键技术叫做"感知哈希算法"(Perceptual Hash Algorithm), 意思是为图片生成一个指纹(字符串格式), 两张图片的指纹越相似, 说明两张图片就越相似. 但关键是如何根据图片计算出"指纹"呢? 下面用最简单的步…

学web前端需要了解哪些常识
想要学好web前端技术,那么一定要掌握足够的知识,web前端技术包含很多方面的知识,具体学web前端需要了解哪些常识?来看看下面的详细介绍。 学web前端需要了解哪些常识? html css javascript。 要学的内容实在很多,如果没有其他编…

linux下后台执行shell脚本
一句话 nohup sh startup_Server.sh & 转载于:https://www.cnblogs.com/phpcode/archive/2012/04/24/2522761.html

线性代数:第一章 线性方程组
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 从本章开始,我们一起来学习线性代数的有关知识,线性代数的应用之一就是求解复杂…

菜鸟也来学习ORACLE(1)_linux下安装oracle 11g
加入 oracle Club 之前,学长给我们开了个小会 说是看看我们加入的意愿,哎哎 其实直无聊,但是大体比较重视linux 服务器的搭建 以及在linux 下安装oracle 搭建一个oracle 环境吧、我就想这东西能有多难,于是回来就搭建起了&#x…

CSS浮动元素特点有什么
什么是浮动? 元素的浮动是指设置了浮动属性(flot)的元素。 CSS浮动有什么作用? 1.让多个盒子水平排列成一行,浮动成为布局的重要手段; 2.可以实现盒子的左右对齐等等; 3.浮动最早是用来控制图片,实现文字环绕图片的效果。 CSS浮动的语法: 选…
数据结构与算法:11 Leetcode同步练习(四)
目录 题目01:最小栈题目02:有效的括号题目03:用队列实现栈题目04:整数反转题目05:逆波兰表达式求值题目06:全排列题目07:字符串转换整数 (atoi)题目08:设计循环双端队列题目09&…
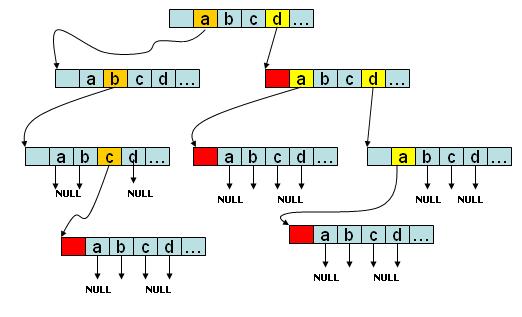
trie树 详解
前几天学习了并查集和trie树,这里总结一下trie。 本文讨论一棵最简单的trie树,基于英文26个字母组成的字符串,讨论插入字符串、判断前缀是否存在、查找字符串等基本操作;至于trie树的删除单个节点实在是少见,故在此…

启动hadoop的节点
1.启动hadoop的节点 start-dfs.sh 本文转自 素颜猪 51CTO博客,原文链接:http://blog.51cto.com/suyanzhu/1959242

什么是Python线程?Python线程如何创建?
相信正在学习Python技术或者对Python语言有一定了解的人对于Python线程应该都不陌生,但是也有刚接触Python的小伙伴对于Python线程并不了解,今天小编就跟大家聊聊什么是Python线程,又该如何创建Python线程! 什么是Python线程?Python线程如何…

ItemAdding实现数据验证--中文字段,properties.AfterProperties值为null的问题
最近写事件接收器,发现中文字段如果直接用properties.AfterProperties[“申请人"]这样获取的值为null,无法得到值。后拉忽然发现用英文字段可以得到值。难道中文字段需要编码?经过测试果真如此。 代码部分如下:public overri…

jstl c:choose、c:when和c:otherwise标签
在用spring mvc中,页面前端老用jstl,记录一下。 <c:choose>、<c:when>和<c:otherwise>在一起连用,可以实现Java语言中的if-else语句的功能。例如以下代码根据username请求参数的值来打印不同的结果: <c:choo…
怎样设计出优秀的测试用例?看看下面就知道了
想要成为一名合格的软件测试工程师,一份合格软件测试报告是非常重要的,软件测试的核心也就是测试的用例了,我们通过用例可以看出怎么设计出来可以发现问题,可以有效的覆盖需求的,没有冗余的用例是每个测试工程师必须跨…
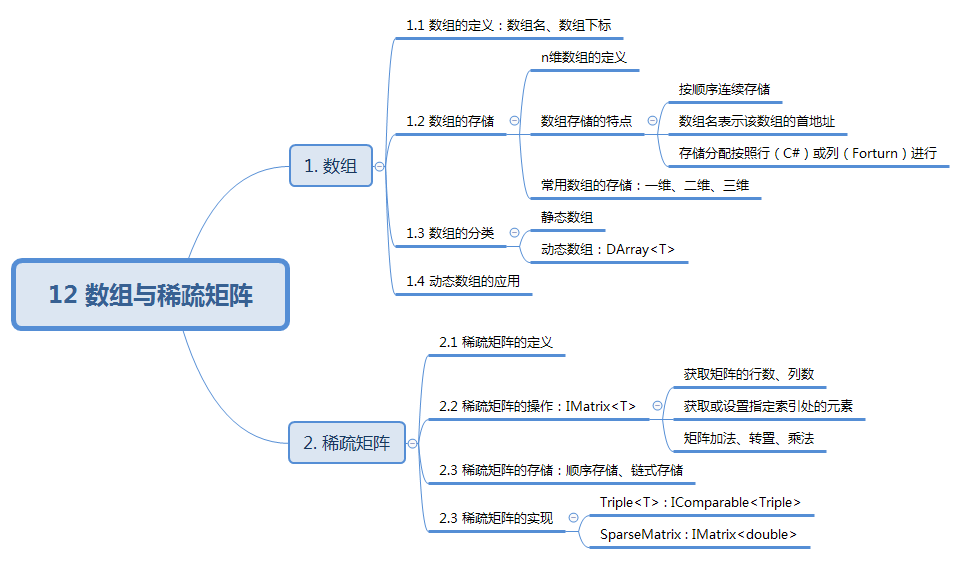
数据结构与算法:12 数组与稀疏矩阵
12 数组与稀疏矩阵 知识结构: 1. 数组 1.1 数组的定义 数组是具有一定顺序关系的若干对象组成的集合,组成数组的对象称为数组元素。 例如: 向量对应一维数组 A(a0,a1,⋯,an−1)A(a_0,a_1,\cdots,a_{n-1}) A(a0,a1,⋯,an−1) 矩阵…

管理索引表:深入研究B树索引--重建,合并,删除(理论篇3)
重建索引 如果表中记录频繁地被删除或插入,尽管表中的记录总量保持不变,索引空间的使用量会不断增加。虽然记录从索引中被删除,但是该记录索引项的使用空间不能被重新使用。因此,如果表变化不定,索引空间量会不断增…

模块架构不是软件成功的“决定因素”
【本文是09年的一篇旧文,出于某些原因,对原文内容有删减,在这里整理后重新发表】 前言感谢XXX对我们技术,对我们公司产品提出这些意见,我们公司卖的是软件产品,开发软件是一件技术活,说实话&…
JavaScript面向对象修改标签页详解
双击标签页组件中的li小标签或者section 中的文本,可以对文本进行编辑。为了实现这个功能,需要先给li和section元素绑定双击事件,当双击文本后,将文本改成一个文本框,用来输入新的内容,在文本框中显示原来的…

