当前位置：首页 > 编程日记 > 正文

数值分析第一次作业-牛顿迭代法求解二元非线性方程组

编程日记 2024-02-20 10:00:00

1、问题

求解如下方程组:

$\left\{ {\begin{array}{*{20}{l}} {f(x,y) = \sin (xy)\exp [ - 0.1*({x^2} + {y^2} + xy + 2x)]}\\ {(x,y) \in [ - 3,1] \times [ - 1,2]} \end{array}} \right.$

2、算法

3、代码实现

# *coding:utf-8 *
import math
delta = 5e-6 ;eps = 1e-6
x0 = 1;y0 = 1
er = 1;k = 0
def z(x,y):return math.sin(x*y)*math.exp(-0.1*(x**2+y**2+x*y+2*x))
def f(x,y):return y*math.cos(x*y)-0.1*(2*x+y+2)*math.sin(x*y)
def g(x,y):return x*math.cos(x*y)-0.1*(2*y+x)*math.sin(x*y)
def f_x(x,y):return -y**2*math.sin(x*y)-0.2*math.sin(x*y)-0.1*(2*x*y+y**2+2*y)* math.cos(x*y)
def f_y(x,y):return math.cos(x*y)-x*y*math.sin(x*y)-0.1*math.sin(x*y)-0.1*(2*x**2+x* y+2*x)*math.cos(x*y)
def g_x(x,y):return math.cos(x*y)-x*y*math.sin(x*y)-0.1*math.sin(x*y)-0.1*(2*y**2+x*y)*math.cos(x*y)
def g_y(x,y):return -x**2*math.sin(x*y)-0.2*math.sin(x*y)-0.1*(2*x*y+x**2)* math.cos(x*y)
print('使用初值为(',"{0:.1f}".format(x0),', ',"{0:.1f}".format(y0),')')
while er > 0.000000001:x1=x0+(f(x0,y0)*g_y(x0,y0)-g(x0,y0)*f_y(x0,y0))/(g_x(x0,y0)*f_y(x0,y0) -f_x(x0,y0)*g_y(x0,y0))y1=y0+(g(x0,y0)*f_x(x0,y0)-f(x0,y0)*g_x(x0,y0))/(g_x(x0,y0)*f_y(x0,y0) -f_x(x0,y0)*g_y(x0,y0))er=max(abs(x1-x0),abs(y1-y0))x0=x1;y0=y1k=k+1print('迭代次数',"{0:.0f}".format(k),',方程根的近似值为x=', "{0:.10f}".format(x1),',y =',"{0:.10f}".format(y1))
print('误差er=',"{0:.16f}".format(er))
print('方程组的根为(',"{0:.10f}".format(x1),',',"{0:.10f}".format(y1),')', "原函数极小值z=","{0:.10f}".format(z(x1, y1)))

当初值为（1，1）时，计算结果如表1。

此时可以得到原二元函数的极小值点为(0.9097471401，1.3180997683)，极小值为0.5330808683。然而，当初值取(-1,-1)时，可以得到原二元函数的极小值点为(-1.5221370100，-0.8914954107)，极小值为0.8474932827。为什么两个结果不一样呢？

4、解决问题

当初值不同时，得到的结果完全不一样，之所以出现这样的结果的原因是因为二元函数可能存在多个极小值点或者鞍点。为了探究原二元函数的三维空间形状，用python画出原二元函数的三维图像如图1，三维图像绘制代码picture_3D.py见附录。

根据图1，可以清晰地看到原二元函数有且只有一个极小值点。旋转矢量图可以看出原二元函数的极小值点大约在x=-1.5，y=1处，极小值大约为-1.1，如图2、图3。。

于是重新取初值为(-1.5,1),并计算结果，如表3。此时可以得到原二元函数的极小值点为(-1.5931730287，0.9721251312)，极小值为-1.1330866542。

附录

# *coding:utf-8 *
import numpy as np
from matplotlib import pyplot as plt
# 定义坐标轴
fig = plt.figure()
ax1 = plt.axes(projection='3d')
# 定义三维数据
xx = np.arange(-3, 1, 0.05)
yy = np.arange(-1, 2, 0.05)
x, y = np.meshgrid(xx, yy)
z = np.sin(x * y) * np.exp(-0.1 * (x ** 2 + y ** 2 + x * y + 2 * x))
# 作图
ax1.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
ax1.contour(x, y, z, stride=0.05, zdim='z', offset=-3, cmap='rainbow')  # 绘制等高线
plt.show()

https://www.dkcj.cn/info/1993.html

Maya制作风格化的女性跑步动画学习教程

时长:2h 11m |视频:. MP4 1280720，30 fps(r) |音频:AAC，48000 Hz，2ch |大小解压后:1.56 GB 含参考素材流派:电子学习|语言：英语中英文字幕（根据原英文字幕机译更准确） 通过在Autodesk Maya中提供专业外观…

编程日记2024/02/20 09:30:00

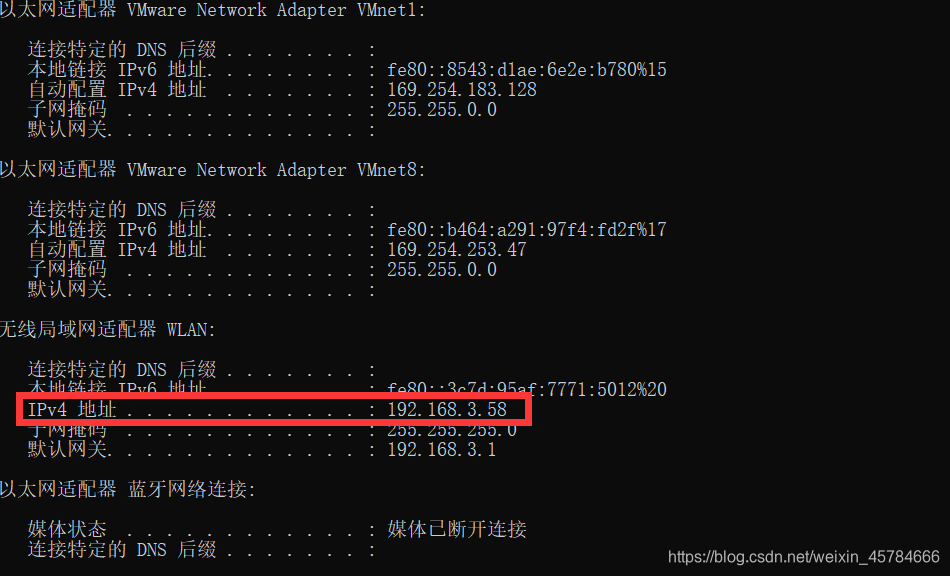
安卓手机抓包实战

最近因为要做一个项目，所以需要对手机给家电发送的请求进行抓取，于是上网找了许多教程，但都不怎么理想，最终经过两个晚上的艰辛奋斗，终于让我找到了方法抓取到了手机发送的请求，写一篇博客记录一下这个过程…

编程日记2024/02/20 09:00:00

导入drupal中文语言包

http://lugir.com/book/export/html/399转载于:https://www.cnblogs.com/qinqiu/p/5174062.html

编程日记2024/02/20 08:30:00

JavaScript引擎大战：Google提出StrongMode和SoundScript议案，增强V8性能

JavaScript 引擎性能大战硝烟迷漫，Chrome V8 引擎团队宣布了一个新的计划，在这个计划里他们介绍了两个新的虚拟机概念：强化模式（StrongMode）和强化脚本（StrongScript）。\\强化模式是 ES5 严格模…

编程日记2024/02/20 07:30:00

数值分析第三次作业-常微分方程的数值解法

一、欧拉方法二、修正的欧拉方法 2.1.梯形公式将问题（*）的解表成积分形式，用数值积分方法离散化。例如，对微分方程

编程日记2024/02/20 07:00:00

SYNCHRO 4D可视化调度学习教程 SYNCHRO 4D: Visual Scheduling

编程日记2024/02/20 06:30:00

SpringBoot复习：4（@ImportResource）

ImportResource注解作用：这个注解可以用来导入Spring的配置文件（bean.xml文件）。适用场景： 可以试想一下这样一个场景，老板要你将原来的Spring项目改成SpringBoot项目，原项目底下有一大堆的bean.xml文件…

编程日记2024/02/20 06:00:00

YTU 2723: 默认参数--求圆的面积

2723: 默认参数--求圆的面积时间限制: 1 Sec 内存限制: 128 MB提交: 206 解决: 150题目描述根据半径r求圆的面积, 如果不指定小数位数,输出结果默认保留两位小数。部分代码已给定如下，只需要提交缺失的代码。 #include <iostream> #include <iomanip&…

编程日记2024/02/20 05:30:00

jmeter内存溢出处理方式记录

方法一： 使用jmeter进行压力测试时遇到一段时间后报内存溢出outfmenmory错误，导致jmeter卡死了，先尝试在jmeter.bat中增加了JVM_ARGS"- Xmx2048m -Xms2048m -Xmn256m -XX:PermSize128m -Xss256k"，但结果运行时间增加了…

编程日记2024/02/20 04:30:00

支持向量机学习笔记1

1、支持向量机是一种二类分类模型。它的模型基本定义是特征空间上间隔最大的线性分类器。 2、核函数的引入，使得支持向量机可以进行非线性分类。 3、支持向量机也可以完成多类别分类（将在后面介绍） 4、支持向量机的学习策略为间隔最大化&a…

编程日记2024/02/20 04:00:00

C4D入门学习教程

MP4 |视频:AVC，1280720 30 fps |音频:AAC，48 KHz，2 Ch |时长:2h 12m 语言：英语中英文字幕（根据原英文字幕机译更准确）|大小解压后:560M C4D是一个有抱负的运动图形艺术家和设计师的重要工具。借助C4D&#…

编程日记2024/02/20 03:30:00

SpringBoot复习：5（配置绑定）

配置绑定在SpringBoot中我们如何读取到properties文件中的内容，并且把它封装到JavaBean中，以供随时使用呢？ 我们可以使用以下两种方式来实现。方法一：ConfigurationPropertiesComponent 第一种方法，我们可以使用C…

编程日记2024/02/20 03:00:00

是男人就下100层【第五层】——2048游戏从源代码到公布市场

上一篇《是男人就下100层【第五层】——换肤版2048游戏》中阳光小强对2048游戏用自己的方式进行了实现，并分享了核心源码，这一篇阳光小强打算将该项目的全部源码公开并结合这个实例在这篇文章中介绍一下怎样加入广告和实现分享功能。终于执行效果例如以下…

编程日记2024/02/20 02:30:01

zabbix菜单出现问号乱码问题

zabbix菜单出现问号乱码问题安装后zabbix，设置成中文后，发现菜单出现了好多的乱码，google之后才知道这与zabbix数据库字符集设置有关。查看当前的默认字符集：mysql> show create database zabbix;---------------------------…

编程日记2024/02/20 01:30:00

什么是Closed-form solution？

最近看论文，讨论微分方程解时遇到closed-form solution概念，上网检索，找到一个较浅显易懂的解释如下。与工学院所学的微分方程不同的是，工学院的学生一般都是学如何把特定的微分方程的解用基本函数（例如多项式、三角函…

编程日记2024/02/20 01:00:00

c4d中的3D插图制作视频教程 Skillshare – 3D Illustration in Cinema 4D

技能分享——C4D的3D插图教程大小解压后：1.33G 1920X1080 mp4 语言：英语中英文字幕（根据原英文字幕机译更准确） C4D是众所周知的平易近人的软件，也是进入3D艺术梦幻世界的理想门户。加入马特的这个课程&#xff0c…

编程日记2024/02/20 00:30:00

SpringSecurity学习：1（第一个SpringSecurity项目）

此博客是记录自己学习过程的记录第一个SpringSecurity项目导入依赖详细的步骤我就不多说了，使用IDEA创建过SpringBoot项目的人一般都能看懂。这一步我们可以在使用IDEA创建SpringBoot项目的时候完成，如下图： 在创建SpringBoot项目时&a…

编程日记2024/02/20 00:00:01

遍历Map<String,Object>遍历Map<Stirng,List<Student>>遍历List<Map<String,Student>>Student.java package action;public class Student {private Long sid;private String name;public Student() {// TODO Auto-generated constructor stub}p…

编程日记2024/02/19 23:30:00

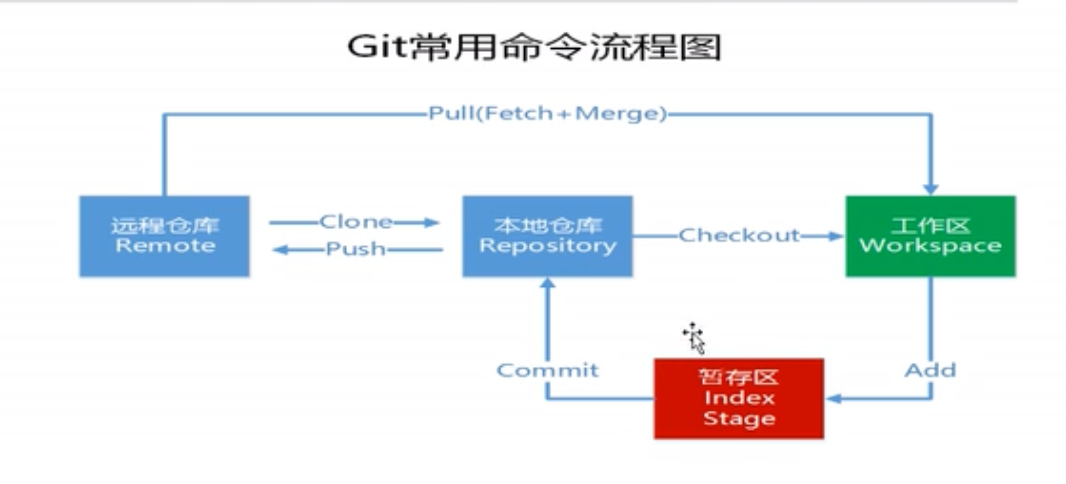
TortoiseGit的使用详解

然后A修改了，A想上传代码，发现冲突了，原因是A依靠的是1版本的代码进行了修改，而此时远程仓库的代码是2版本，这样当然会产生冲突。当从远程仓库拉取代码时，代码会直接拉取到工作区，然后我们要添加、提交，然后才可以把拉取的代码放入本地仓库，本地仓库的代码可以通过推送，推送到远程仓库，这是一个大循环。解决冲突的办法就是，先把远程仓库的2版本的代码进行拉取，然后TortoiseGit会列出冲突的文件代码，然后自己手动解决、选择自己需要的代码，右键选择解决冲突，最后再重新上传就可以了。点击拉取，可以下载文件。

编程日记2024/02/19 22:30:03

数值分析第一次作业-牛顿迭代法求解二元非线性方程组

1、问题

2、算法

3、代码实现

4、解决问题

附录

相关文章：

Maya制作风格化的女性跑步动画学习教程

安卓手机抓包实战

导入drupal中文语言包

JavaScript引擎大战：Google提出StrongMode和SoundScript议案，增强V8性能

数值分析第三次作业-常微分方程的数值解法

SYNCHRO 4D可视化调度学习教程 SYNCHRO 4D: Visual Scheduling

SpringBoot复习：4（@ImportResource）

YTU 2723: 默认参数--求圆的面积

jmeter内存溢出处理方式记录

支持向量机学习笔记1

C4D入门学习教程

SpringBoot复习：5（配置绑定）

是男人就下100层【第五层】——2048游戏从源代码到公布市场

zabbix菜单出现问号乱码问题

什么是Closed-form solution？

c4d中的3D插图制作视频教程 Skillshare – 3D Illustration in Cinema 4D

SpringSecurity学习：1（第一个SpringSecurity项目）

使用Struts2标签遍历集合

TortoiseGit的使用详解

Java的System.out.println()深入解析理解

第一次作业，针对软件工程这门课程提出五个疑问。

matlab2013 a/b 找不到vs2013 c++ 编译器解决方案

C4D运动图形基本训练学习教程

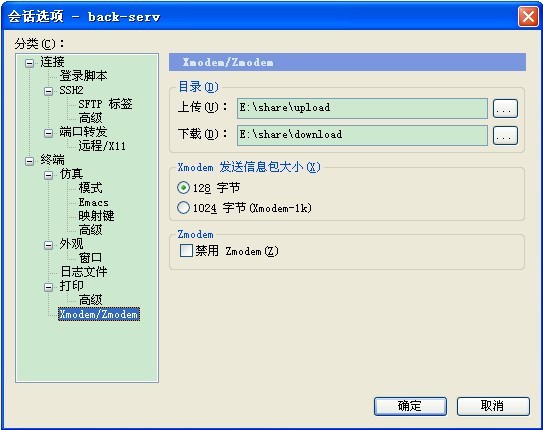
linux快捷上传下载文件

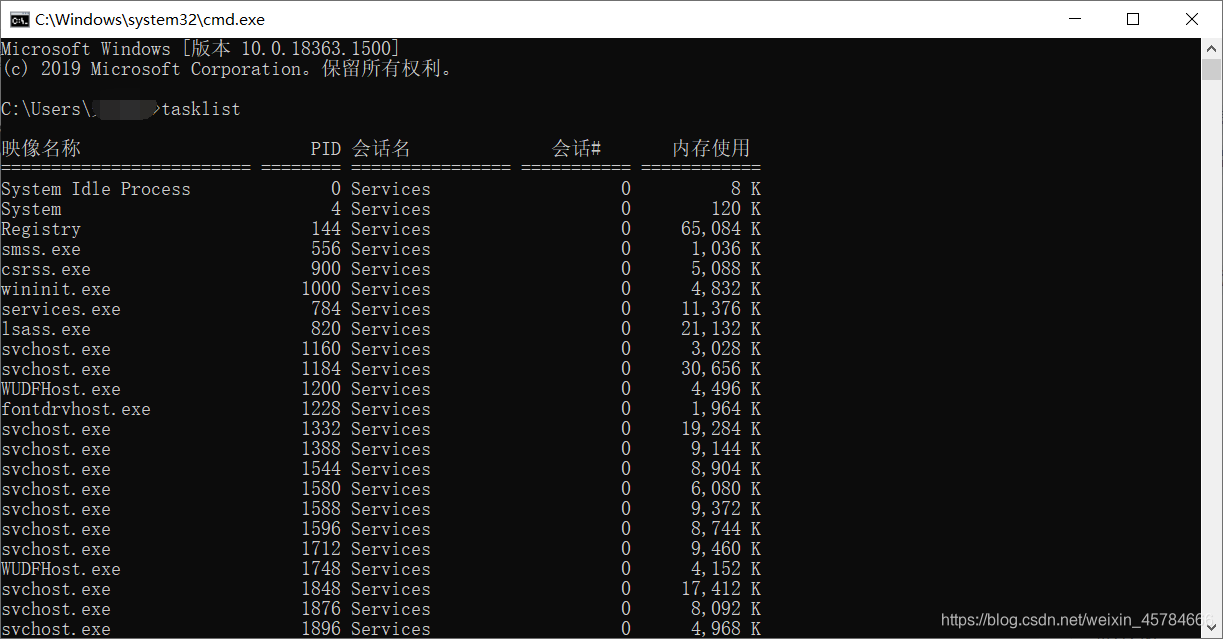
Java多线程复习：3（在操作系统中查看和杀死进程线程）

Adt 配置注释模板

解决Attempt to execute SCRIPT mexLasso as a function

灰猩猩拓扑速成班

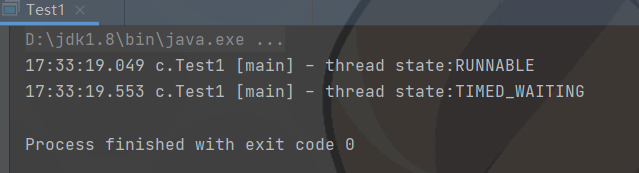
Java多线程复习：5（sleep、yield方法和线程优先级）

Atitit.java jna 调用c c++ dll的原理与实践总结 v2 q27