什么是Closed-form solution?
最近看论文,讨论微分方程解时遇到closed-form solution概念,上网检索,找到一个较浅显易懂的解释如下。
与工学院所学的微分方程不同的是,工学院的学生一般都是学如何把特定的微分方程的解用基本函数(例如多项式、三角函数、对数指数函数等等)及特殊函数给表达出来(所谓的 closed form solution)。然而,在一般的情况下,要找 closed form solution 是极其困难甚至是不可能的。所以从数学的眼光来看,第一步往往是问微分方程的解是否存在(存在是表示知道有函数会满足微分方程,但是不见得是 closed form solution 或是其它写得出来的样子,而只是就知道有解,玄吧?),若能证明解的存在性,那么下一个问题便是:解是否唯一(在很多情况下,解可能会是两个以上,此时就会衍生一个问题:哪个解比较合乎自然现象的结果)。这两个问题虽然看来非常像是哲学的问题(例如物理学家一定觉得明明自然的现象每天都在进行,而那些方程都是在描述自然的现象,解怎么可能不存在?或是哲学家问上帝存不存在、唯不唯一的问题,记得,就算证明了存在,还是看不到,这跟数学很像),但是往往研究这两件事的过程中会让人对所研究的微分方程有更多的了解,所以从某个角度而言数学的研究有其必要。而再往另一个更实际的方面来说,能写出 closed form solution 的微分方程,往往不一定能马上从解看出原方程所描述的现象。例如抛物型方程常常扮随有扩散的效应,也就是说所关心的物理量(例如浓度、温度)会由量高的地方往量低处流动;而双曲型方程却常是满足守恒律,也就是说若某物理量在某一时间点的最大值是这么大,那么这个值永远这么大不会「扩散」掉。这种现象上的分野是很难直接从方程的解本身看出来的,所以我想用一句很贴切的话来说明解在微分方程中的地位:叫做见树不见林里面的「树」(而林则是指微分方程所描写的现象本身)。数学的研究方法,即在从方程的本身(而非从树),去推敲林的长相。
然而,解的本身仍然是对了解微分方程所描述的自然现象,相当不可或缺的一部份。诚如前面所谈到的,要求解往往是极为困难的工作,所以数值方法的发展在某种程度上弥补了这个空隙。
附:庞加莱的微分方程定性理论
从微分方程产生到1820年,微分方程理论的唯一问题是:找到给定微分方程的解析解。然而随着研究的扩展和深入,人们遗憾地发现可以解析求解的常微分方程类型甚少。大量出现在物理学、工程技术及其他实际问题中的常微分方程通常都是非线性的。客观求解的需要与大多数解不能用初等函数及其积分表示的矛盾日益凸显。
就在人们为非线性微分方程没有普遍解法无法解决苦恼时,法国数学家庞加莱提示必须改变思考方式,因为试图写出表达式和积分的定量方法只能解决某些问题,即使不能找到精确解,仍可以利用定性的和几何的思考获得解的许多性质。
1881年到1886年,庞加莱发表了《关于由微分方程确定的曲线的报告》的一系列论文,开创了常微分方程实域定性理论。天文学、物理学、工程技术中的微分方程有时不必求出确定解,只要知道解的某些性质即可,而定性思想恰好成为精确性和模糊性辩证统一的契合点。庞加莱在微分方程定量研究的基础上引入定性理论,在理论和实际应用中都发挥了重要的作用。他创造了无切环(不与任何满足微分方程的曲线相切的闭曲线)等新的数学方法。在研究过程中开辟出实域定性理论、组合拓扑学两个重要的数学分支。
庞加莱认为,对一个函数完整的研究应包括定性和定量两部分:即函数定义下曲线的几何研究;函数值的数值计算。以前研究代数函数时总试图将其化简为根式,而现在大多数先用施图姆定理找到实根的个数,再计算根的数值。
庞加莱直接研究微分方程定义的函数,而不是将其简化形式。他先构造出方程定义的曲线,确定出一定数量的点,以此作为定量研究的基础。其实,许多极为重要的分析和力学问题也由此可以转化为定性研究。
庞加莱的定性研究之所以能取得丰硕成果,很大程度上取决于他选择了几何直观的方法。实质是:在不求解的情况下,直接考察微分方程的系数和结构,分析和推断积分曲线可能具有的各种特性,如曲线的形状、结构和趋势等,从而研究解的性质。
几何方法比分析方法更加全面直观,许多分析难以直接解决的问题往往利用几何进行整体的考虑获得解答。而且,几何已是一门较为成熟完善的学科,具有许多经典的性质和方法,是解决数学难题的利器。
在这种思路指引下,研究对象也逐渐由函数转向曲线。庞加莱认为,利用方程定义的曲线可以较完整、直观地描述出解的特性;而把微分方程的解表示成函数形式会对几何直观造成障碍。庞加莱选择微分方程定义的积分曲线作为研究对象,使其成为研究微分方程解的性质的有效手段。
庞加莱在研究微分方程解的性质时,为避免研究无穷分支,先将一个平面投影到一个球面上,然后用微分方程把每一个确定方向与球面上的每一点联系起来,确定投影在整个球面的积分曲线形式。
数学家在微分方程求解过程中不懈努力,使许多特殊类型的一阶方程有较成熟的解法,对复杂的高阶方程则利用分离变量法化为低阶问题解决。在方程不能以封闭形式解出时,欧拉等人又采取级数展开法求近似解。但这些方法都没有根本摆脱求确定解的桎梏,使研究的道路越来越窄。
其实,在科学探索中求“是”存在困难时,可以转而通过求“否”去界定研究对象的性质和范围,从而达到求“是”的目的,这是科学思想中最重要的方法之一。庞加莱就将这种简单有效的思想方法广泛应用于微分方程定性理论中。
微分方程定义下的积分曲线与无切曲线的关系就类似于等式与不等式的关系。当解等式较难时,可以用不等式的解来界定等式的解。庞加莱没有直接确定积分曲线,而是利用无切环确定出极限环,从而获得微分方程解的基本性态。
法国科学院院士阿达玛(J.Hadamard)在《亨利·庞加莱的科学工作》一书中称无切环概念为“非积分”,以便与微分方程的“积分”相对比,正如不等式与等式的关系。“无切环” 与“无切弧”等概念是庞加莱对实域定性理论引入的主要工具,是将等式转为不等式的研究、将分析工具转为几何工具的体现。
庞加莱将定性理论应用到微分方程解的研究中,引发了一系列理论研究的新变革、新突破,同时也使人们对定性思想的认识提升到了新的高度。
庞加莱强调定性方法是以有实值解为最终目的。他认为,在数学分析研究中几何与几何直觉应当发挥新作用,但这种创新应保证分析的中心地位不变,甚至应当被加强。几何-定性方法的引入只表明分析可行领域的扩大和它解释说明能力的增强,而不是分析让位给几何。庞加莱虽以定性理论成为一位创新者,但这种创新仍是在经典数学理论基础上的创新。
虽然在庞加莱生前定性分析的意义未受到重视,但是他引入的几何方法,恰如其分地处理了分析与几何的关系,使定性分析成为复兴和发展数学分析的最有力武器。
庞加莱创立的定性理论是微分方程发展过程中的一次新突破,促成20世纪以来微分方程的进一步发展。在此基础上,人们针对各种具体问题进行了深入的研究,如俄国杰出数学家李雅普诺夫(A.M.Liapunov)的运动稳定性理论和美国数学家伯克霍夫(G.D.Birkhoff)的动力系统研究。随着定性理论的日趋成熟和完善,微分方程的研究也转入了新的定量分析时期。
文章转自:http://belobaba.blog.163.com/blog/static/11534314820096263443219/
相关文章:

c4d中的3D插图制作视频教程 Skillshare – 3D Illustration in Cinema 4D
技能分享——C4D的3D插图 教程大小解压后:1.33G 1920X1080 mp4 语言:英语中英文字幕(根据原英文字幕机译更准确) C4D是众所周知的平易近人的软件,也是进入3D艺术梦幻世界的理想门户。 加入马特的这个课程,…

SpringSecurity学习:1(第一个SpringSecurity项目)
此博客是记录自己学习过程的记录 第一个SpringSecurity项目 导入依赖 详细的步骤我就不多说了,使用IDEA创建过SpringBoot项目的人一般都能看懂。 这一步我们可以在使用IDEA创建SpringBoot项目的时候完成,如下图: 在创建SpringBoot项目时&a…

使用Struts2标签遍历集合
遍历Map<String,Object>遍历Map<Stirng,List<Student>>遍历List<Map<String,Student>>Student.java package action;public class Student {private Long sid;private String name;public Student() {// TODO Auto-generated constructor stub}p…
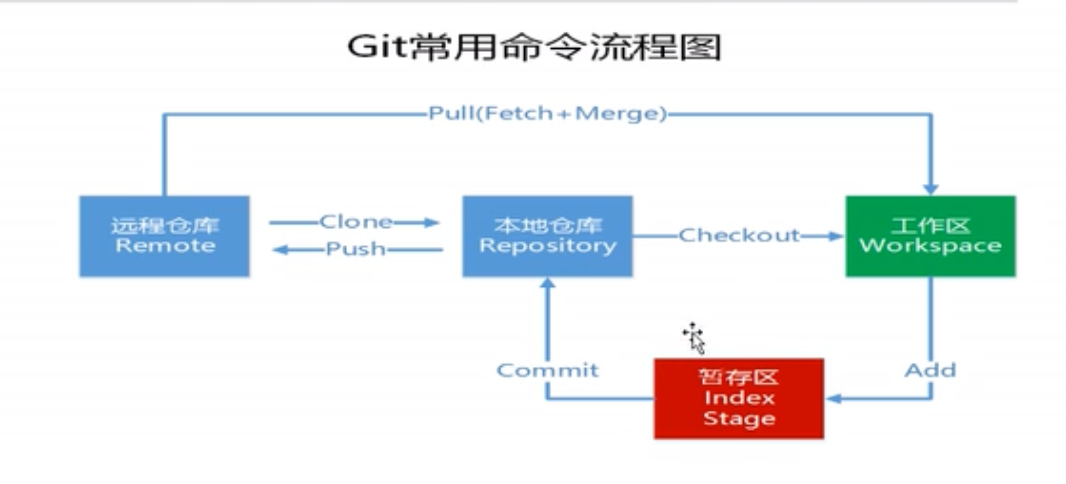
TortoiseGit的使用详解
然后A修改了,A想上传代码,发现冲突了,原因是A依靠的是1版本的代码进行了修改,而此时远程仓库的代码是2版本,这样当然会产生冲突。当从远程仓库拉取代码时,代码会直接拉取到工作区,然后我们要添加、提交,然后才可以把拉取的代码放入本地仓库,本地仓库的代码可以通过推送,推送到远程仓库,这是一个大循环。解决冲突的办法就是,先把远程仓库的2版本的代码进行拉取,然后TortoiseGit会列出冲突的文件代码,然后自己手动解决、选择自己需要的代码,右键选择解决冲突,最后再重新上传就可以了。点击拉取,可以下载文件。

Java的System.out.println()深入解析理解
语句来输出信息,从开始学习Java就知道用它来输出Hello World,没有深究其实现原理,现在查阅文档、源代码后记录一下。方法进行字符流输出,只是整个过程封装了许多方法来支持各种类型的变量、以及自动初始化等,使得用户能够方便快捷在控制台打印数据。变量进行了初始化,让它指向控制台,于是就可以直接使用了。的,因此即使程序中没有手动导入,也可访问到。由C/C++实现,这里只是一个接口,在。修饰的,根据Java语法,它只能调用。方法重载,因此可输出多种类型的数据。接着看,在构造方法中,先是初始化了。

第一次作业,针对软件工程这门课程提出五个疑问。
1、如果对于不爱好计算机的同学来说学习软件工程的意义大吗,有多大? 2、软件工程的知识面那么广,如果才能系统有效的将它学好? 3、软建工程这门课是否有点纸上谈兵了? 4、软件工程是衣门很枯燥的学科,我们怎…

matlab2013 a/b 找不到vs2013 c++ 编译器 解决方案
64-bit Matlab 解压附件后,放到 C:\Program Files\MATLAB\R2013a\bin\win64\mexopts32-bit Matlab 解压附件后,放到 C:\Program Files\MATLAB\R2013a\bin\win32\mexopts点我下载附件 原文出处:http://kaba.hilvi.org/homepage/blog/vs_201…

C4D运动图形基本训练学习教程
MP4 |视频:h264,1280720 |音频:AAC,44.1 KHz,2 Ch 技能水平:初级|语言:英语中英文字幕(根据原英文字幕机译更准确) |持续时间:3h 1m |大小解压后:1.7 GB 含课程练习文件 C4D继续作为3D艺术家的行业标准解决…
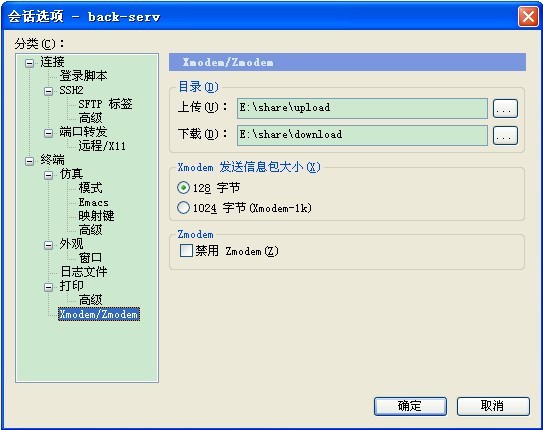
linux快捷上传下载文件
借助securtCRT,使用linux命令sz可以很方便的将服务器上的文件下载到本地,使用rz命令则是把本地文件上传到服务器 其中,对于sz和rz的理解与记忆我用了如下的方法(因为很多时候容易搞混):sz中的s意为send&…
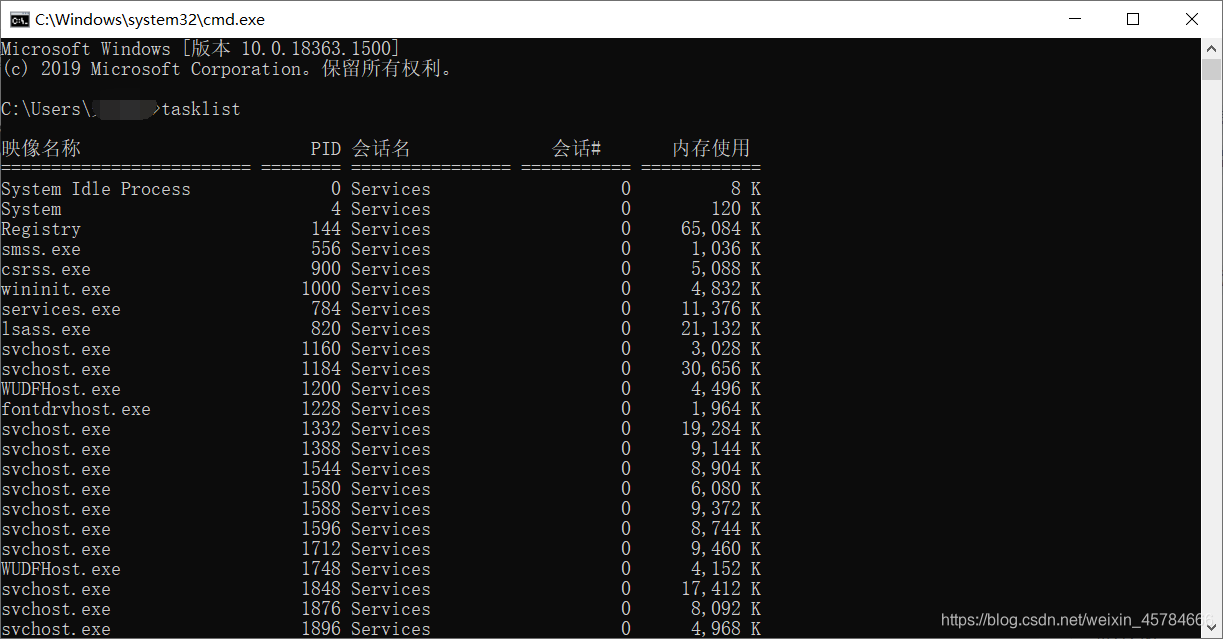
Java多线程复习:3(在操作系统中查看和杀死进程线程)
此博客是记录自己学习过程的记录,仅做参考 Windows下查看和杀死进程线程 查看所有进程 tasklist 查看指定关键字的进程 tasklist | findstr 关键字 Java程序运行的时候都是通过java.exe来运行的,所以想要查看Java程序运行的详情的话必须使用jdk自带的命…

Adt 配置注释模板
点击Window->Preferences->Java->Code Style->Code Templates,如下图所示: 选中,点击右侧的Edit进行编辑。

解决Attempt to execute SCRIPT mexLasso as a function
Attempt to execute SCRIPT mexLasso as a function: Error in selectFeature (line 22)w mexLasso(L, A, param);Error in demo (line 62)P selectFeature(AA_pos, AA_neg, paramSR); % feature selection 遇到这个问题一般是因为名为mexLasso的文件与…

灰猩猩拓扑速成班
Greyscalegorilla Plus Topology Crash Course 灰猩猩附加拓扑速成班 大小解压后:5.62G 1920X1080 时长:1小时16分 语言:英语中英文字幕(机译) 信息: 这个拓扑速成课程正如其名。它将为您提供坚实的拓扑基础…
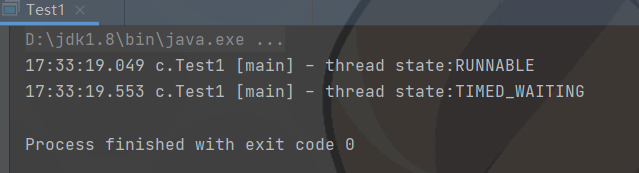
Java多线程复习:5(sleep、yield方法和线程优先级)
sleep、yield方法和线程优先级 sleep方法 调用 sleep 会让当前线程从 Running 进入 Timed Waiting 状态(阻塞);其它线程可以使用 interrupt 方法打断正在睡眠的线程,这时 sleep 方法会抛出 InterruptedException;睡眠…

Atitit.java jna 调用c c++ dll的原理与实践 总结 v2 q27
Atitit.java jna 调用c c dll的原理与实践 总结 v2 q27 1. Jna简单介绍1 2. Jna范例halo owrld1 3. Jna概念2 3.1. (1)需要定义一个接口,继承自Library 或StdCallLibrary2 3.2. 2)接口内部定义2 4. 数据类型映射 NA官方给出的…

Android自定义控件系列之基础篇
一、概述在android开发中很多UI控件往往需要进行定制以满足应用的需要或达到更加的效果,接下来就通过一个系列来介绍自定义控件,这里更多是通过一些案例逐步去学习,本系列有一些典型的应用,掌握好了大家也可去创新开发出一些更好的UI…
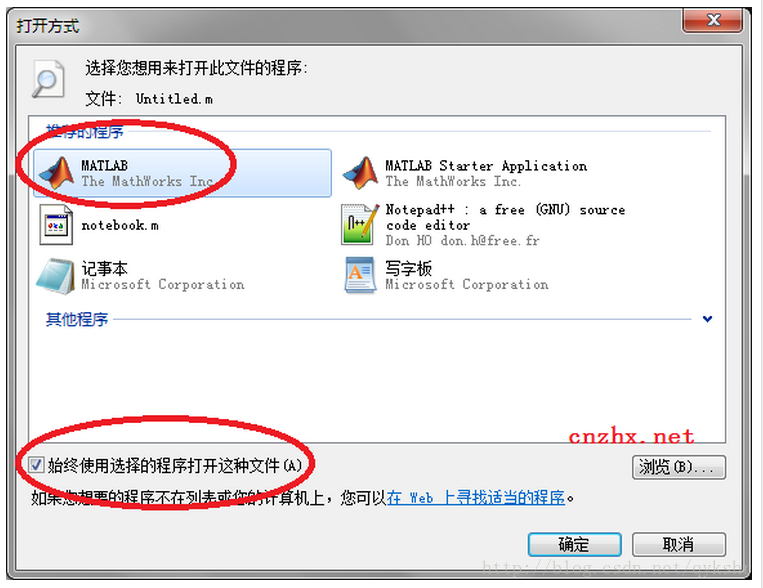
用matlab编辑器打开.m文件
1、复制如下代码在,matlab命令行里运行 commandwindow; cwdpwd; cd([matlabroot \toolbox\matlab\winfun\private]); fileassoc(add,{.m,.mat,.fig,.p,.mdl,[. mexext]}); % 重点,增加了多种文件类型 cd(cwd); disp(Changed Windows file associations.…

Unity制作2D动作平台游戏视频教程
Metroidvania工具包:打造统一的2D行动平台 流派:电子学习| MP4 |视频:h264,1280720 |音频:AAC,48.0 KHz 语言:英语中英文字幕(根据原英文字幕机译更准确)|大小解压后:8.96 GB |时长:20h 53m 学习用C#编码,…

Redis初学:1(NoSQL的简介和Redis的安装)
什么是NoSQL NoSQL数据库意即:Not Only SQL 不仅仅是SQL,它区别于传统的关系型数据库,储存方式按照的是key-value的形式存储数据,这个我们可以联想到我们以前学过的HashMap。 NoSQL的特点: 语法上区别于传统的SQL语句…

函数指针amp;绑定: boost::functoin/std::function/bind
see link: https://isocpp.org/wiki/faq/pointers-to-members function vs template: http://stackoverflow.com/questions/14677997/stdfunction-vs-template boost::functoin/std::function可用于全部 operator() 操作的对象(函数,类。成员…

Python编程规范及性能优化
为什么80%的码农都做不了架构师?>>> Ptyhon编程规范 编码 所有的 Python 脚本文件都应在文件头标上 # -*- coding:utf-8 -*- 。设置编辑器,默认保存为 utf-8 格式。 注释 业界普遍认同 Python 的注释分为两种的概念,一种是由 # 开…

Matlab 快捷键 设置
把Matlab的快捷键都和Windows平台上的保持一致。设置方法:[File]->[Preferences]->[Command Window]->[Keyboard & indenting]->[command line key bindings][File]->[Preferences]->[Editor/Debugger]->[Keyboard & indenting]->[…

Maya与Substance Painter风格化材质阴影和照明学习教程
大小解压后:619 M 1920X1080 mp4 时长:第一部分 48分55秒 第二部分 32分29秒 语言:英语中英文字幕(根据原英文字幕机译更准确) 第一部分介绍Substance Painter风格化材质制作 第二部分介绍Maya中灯光及阴影的学习技…

Deep learning的一些教程 (转载)
几个不错的深度学习教程,基本都有视频和演讲稿。附两篇综述文章和一副漫画。还有一些以后补充。 Jeff Dean 2013 Stanford http://i.stanford.edu/infoseminar/dean.pdf 一个对DL能干什么的入门级介绍,主要涉及Google在语音识别、图像处理和自然语言处理…

Redis初学:2(Redis的启动)
Redis有两种启动方式 前台启动(不推荐) 直接使用命令redis-server,执行结果如下图: 想要退出直接按ctrlc即可 后台启动(推荐) 先在redis的安装目录下复制redis.conf文件到任意一个文件夹底下然后将red…

iOS开发系列--通知与消息机制
http://www.cocoachina.com/ios/20150318/11364.html 概述 在多数移动应用中任何时候都只能有一个应用程序处于活跃状态,如果其他应用此刻发生了一些用户感兴趣的那么通过通知机制就可以告诉用户此时发生的事情。iOS中通知机制又叫消息机制,其包括两类&a…

解决Undefined function or method 'vgg_kmiter' for input arguments of type 'double'.
Undefined function or method vgg_kmiter for input arguments of type double. Error in > vgg_kmeans at 32 [CX, sse] vgg_kmiter(X, CX); 解决方法: 由于高matlab版本不再支持mxCreateScalarDouble,而被变为mxCreateDoubleScalar.因而把所…

C#和Unity游戏开发者大师班2021 (2D,3D和FPS)
流派:电子学习| MP4 |视频:h264,1280720 |音频:AAC,44.1 KHz 语言:英语中英文字幕(根据原英文字幕机译更准确) |大小:11.1 GB |时长:22h 31m 含项目文件 创建你的第一个Unity游戏-水果忍者克隆,豪斯梅斯特…

Redis初学:4(Redis的常用命令)
Redis的常用命令 查看所有key keys *如下图: 插入key set key value如下图: 取出key对应的value值 get key如下图: 查看某个key是否存在 exists key如下图: 1表存在这个key,0表示不存在 判断某个key是什么…

计算多项式的值
总时间限制: 1000ms内存限制: 65536kB描述对于多项式f(x) ax3 bx2 cx d 和给定的a, b, c, d, x,计算f(x)的值。 输入输入仅一行,包含5个实数,分别是x,及参数a、b、c、d的值,每个数都是绝对值不超过100的双精度浮点…
