【优秀作业】蚁群优化算法
蚁群优化算法
一.概述
生物学家发现,自然界中的蚁群觅食是一种群体性行为,并非单只蚂蚁自行寻找食物源。蚂蚁在寻找食物源时,会在其经过的路径上释放一种信息素,并能够感知其它蚂蚁释放的信息素。信息素浓度的大小表征到食物源路径的远近,信息素浓度越高,表示对应的路径距离越短。通常,蚂蚁会以较大的概率优先选择信息素浓度较高的路径,并释放一定量的信息素,以增强该条路径上的信息素浓度,这样会形成一个正反馈。最终,蚂蚁能够找到一条从巢穴到食物源的最佳路径,即最短距离。值得一提的是,生物学家同时发现,路径上的信息素浓度会随着时间的推进而逐渐衰减。
20世纪90年代初,意大利学者M.Dorigo等人提出了模拟自然界蚂蚁群体觅食行为的蚁群算法。其基本思想是:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上积累的信息素浓度逐渐增高,选择该路径上的蚂蚁个数也越来越多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
二.蚁群算法解决TSP问题
1. 算法原理
M.Dorigo等人最早将蚁群算法用于解决旅行商问题(Traveling Salesman Problem,TSP),并取得了较好的实验结果。设整个蚂蚁群体中蚂蚁的数量为 mmm,城市的数量为nnn,城市iii与城市jjj之间的距离为dij(i,j=1,2,⋯,n)d_{ij} (i,j=1,2,\cdots,n)dij(i,j=1,2,⋯,n),ttt时刻城市iii与城市jjj连接路径上的信息素浓度为τij(t)\tau_{ij}(t)τij(t)。初始时刻,各个城市间连接路径上的信息素浓度相同,不妨设τij(0)=τ0\tau_{ij} (0)=\tau_{0}τij(0)=τ0。
蚂蚁k(k=1,2,⋯,m)k(k=1,2,\cdots,m)k(k=1,2,⋯,m)根据各个城市间连接路径上的信息素浓度决定下一个访问城市,设Pijk(t)P_{ij}^k(t)Pijk(t)表示ttt时刻蚂蚁kkk从城市iii转移到城市jjj的转移概率,其公式为:
Pijk={[τij(t)]α×[ηij(t)]β∑s∈allowk[τis(t)]α×[ηis(t)]β,s∈allowk0,s∉allowk\Large P_{ij}^k = \left \{ \begin{array}{l} \frac{[\tau_{ij}(t)]^\alpha\times[\eta_{ij}(t)]^\beta}{\sum_{s\in allow_k}[\tau_{is}(t)]^\alpha\times[\eta_{is}(t)]^\beta} , s\in allow_{k}\\ 0, s\notin allow_{k}\\ \end{array} \right. Pijk=⎩⎪⎨⎪⎧∑s∈allowk[τis(t)]α×[ηis(t)]β[τij(t)]α×[ηij(t)]β,s∈allowk0,s∈/allowk
其中:ηij(t)=1dij\eta_{ij}(t)=\frac{1}{d_{ij}}ηij(t)=dij1为启发函数,表示蚂蚁从城市iii转移到城市jjj的期望程度;allowk(k=1,2,⋯,m)allow_k(k=1,2,\cdots,m)allowk(k=1,2,⋯,m)为蚂蚁kkk待访问城市的集合,开始时,allowkallow_kallowk中有(n−1)(n-1)(n−1)个元素,即包括除了蚂蚁kkk出发城市的所有其它城市,随着时间的推进,allowkallow_kallowk中的元素不断减少,直至为空,即表示所有的城市均访问完毕;α\alphaα为信息素重要程度因子,其值越大,表示信息素的浓度在转移中起的作用越大;β\betaβ为启发函数重要程度因子,其值越大,表示启发函数在转移中的作用越大,即蚂蚁会以较大的概率转移到距离短的城市。当α=0\alpha=0α=0时,算法就是传统的贪心算法,而当β=0\beta=0β=0时,就成了纯粹的正反馈的启发式算法。经过nnn个时刻,蚂蚁可以走完所有的城市,完成一次循环,每只蚂蚁所走过的路径就是一个解。
由于蚂蚁释放信息素的同时,各个城市间连接路径上的信息素逐渐消失,设参数ρ(0<ρ<1)\rho(0<\rho<1)ρ(0<ρ<1)表示信息素的挥发程度。因此,当所有蚂蚁完成一次循环后,各个城市间连接路径上的信息素浓度需进行实时更新,即
{τij(t+1)=(1−ρ)τij(t)+ΔτijΔτij=∑k=1mΔτijk,0<ρ<1\left \{ \begin{array}{l} \tau_{ij}(t+1)=(1-\rho)\tau_{ij}(t)+\Delta\tau_{ij}\\ \Delta\tau_{ij}=\sum_{k=1}^{m}{\Delta\tau_{ij}^k}\\ \end{array} \right.,0<\rho<1 {τij(t+1)=(1−ρ)τij(t)+ΔτijΔτij=∑k=1mΔτijk,0<ρ<1
其中,Δτijk\Delta\tau_{ij}^kΔτijk表示第kkk只蚂蚁在城市iii与城市jjj连接路径上释放的信息素浓度;Δτij\Delta\tau_{ij}Δτij表示所有蚂蚁在城市iii与城市jjj连接路径上释放的信息素浓度之和。
针对蚂蚁释放信息素问题,M.Dorigo等人曾给出3种不同的模型,分别称之为Ant Cycle System、Ant Quantity System和Ant Density System,其计算公式如下:
(1)Ant Cycle System模型
Δτijk={QLk,第k只蚂蚁从城市i访问城市j0,其它\Delta\tau_{ij}^k = \left \{ \begin{array}{l} \frac{Q}{L_k},第k只蚂蚁从城市i访问城市j\\ 0,其它\\ \end{array} \right. Δτijk={LkQ,第k只蚂蚁从城市i访问城市j0,其它
其中,QQQ为常数,表示蚂蚁循环一次所释放的信息素总量;LkL_kLk为第kkk只蚂蚁经过路径的长度。
(2)Ant Quantity System
Δτijk={Qdij,第k只蚂蚁从城市i访问城市j0,其它\Delta\tau_{ij}^k = \left \{ \begin{array}{l} \frac{Q}{d_{ij}},第k只蚂蚁从城市i访问城市j\\ 0,其它\\ \end{array} \right. Δτijk={dijQ,第k只蚂蚁从城市i访问城市j0,其它
(3)Ant Density System
Δτijk={Q,第k只蚂蚁从城市i访问城市j0,其它\Delta\tau_{ij}^k = \left \{ \begin{array}{l} Q,第k只蚂蚁从城市i访问城市j\\ 0,其它\\ \end{array} \right. Δτijk={Q,第k只蚂蚁从城市i访问城市j0,其它
上述3种模型中,Ant Cycle System模型利用蚂蚁经过路径的整体信息(经过路径的总长)计算释放的信息素浓度;Ant Quantity System模型利用蚂蚁经过路径的局部信息(经过各个城市间的距离)计算释放的信息素浓度;Ant Density System模型更为简单地将信息素释放的浓度取为恒值,并没有考虑不同蚂蚁经过路径长度的影响。因此,一般选用Ant Cycle System模型计算释放的信息素浓度,即蚂蚁经过的路径越短,释放的信息素浓度越高。
2. 算法步骤
步骤1:初始化参数
在计算之初,需要对相关参数进行初始化,如蚁群规模(蚂蚁数量)mmm、信息素重要程度因子α\alphaα、启发函数重要程度因子β\betaβ、信息素挥发程度因子ρ\rhoρ、信息素释放总量QQQ、最大迭代次数iter_maxiter\_maxiter_max。
注:在初始化之前需要根据城市位置坐标,计算两两城市间的相互距离,从而得到对称的距离矩阵。由于启发函数为ηij(t)=1dij\eta_{ij} (t)=\frac{1}{d_{ij}}ηij(t)=dij1,为了保证分母不为零,需要将对角线上的元素零,修正为一个非常小的正数(如10−410^{-4}10−4或10−510^{-5}10−5等)。
步骤2:构建解空间
将各个蚂蚁随机地置于不同出发点,对每个蚂蚁k(k=1,2,⋯,m)k(k=1,2,\cdots,m)k(k=1,2,⋯,m),按照转移概率计算公式,确定其下一个待访问的城市,直到所有蚂蚁访问完所有的城市,即构造完一组路径。
步骤3:更新信息素
计算各个蚂蚁经过的路径长度Lk(k=1,2,⋯,m)L_k (k=1,2,\cdots,m)Lk(k=1,2,⋯,m),根据信息素迭代公式对各个城市路径上的信息素浓度进行更新。同时,记录当前迭代次数中的最优解(最短路径)。
步骤4:判断是否终止
若达到最大迭代次数,则终止计算,输出最优解。否则,清空蚂蚁经过路径的记录表,并返回步骤2。
三. 利用蚁群算法求解旅行商问题
按照枚举法,我国 34 个直辖市、省会和自治区首府的巡回路径应有 34! 种。但是那种巡回路径最短呢,我们可以利用蚁群算法进行求解。
城市坐标如下表所示:
| 序号 | 城市 | 到0°经线距离(X) | 到赤道距离(Y) |
|---|---|---|---|
| 1 | 北京 | 9932 | 4439 |
| 2 | 天津 | 10109 | 4351 |
| 3 | 上海 | 11552 | 3472 |
| 4 | 重庆 | 10302 | 3290 |
| 5 | 拉萨 | 8776 | 3333 |
| 6 | 乌鲁木齐 | 7040 | 4867 |
| 7 | 银川 | 9252 | 4278 |
| 8 | 呼和浩特 | 9395 | 4539 |
| 9 | 南宁 | 11101 | 2540 |
| 10 | 哈尔滨 | 9825 | 5087 |
| 11 | 长春 | 10047 | 4879 |
| 12 | 沈阳 | 10227 | 4648 |
| 13 | 石家庄 | 10027 | 4229 |
| 14 | 太原 | 9878 | 4211 |
| 15 | 西宁 | 9087 | 4065 |
| 16 | 济南 | 10438 | 4075 |
| 17 | 郑州 | 10382 | 3865 |
| 18 | 南京 | 11196 | 3563 |
| 19 | 合肥 | 11075 | 3543 |
| 20 | 杭州 | 11544 | 3365 |
| 21 | 福州 | 11915 | 2900 |
| 22 | 南昌 | 11305 | 3189 |
| 23 | 长沙 | 11073 | 3137 |
| 24 | 武汉 | 10950 | 3394 |
| 25 | 广州 | 11576 | 2575 |
| 26 | 台北 | 12239 | 2785 |
| 27 | 海口 | 11529 | 2226 |
| 28 | 兰州 | 9328 | 4006 |
| 29 | 西安 | 10012 | 3811 |
| 30 | 成都 | 9952 | 3410 |
| 31 | 贵阳 | 10612 | 2954 |
| 32 | 昆明 | 10349 | 2784 |
| 33 | 香港 | 11747 | 2469 |
| 34 | 澳门 | 11673 | 2461 |
代码如下:
%% 清空环境变量
clear
clc
close all%% 导入数据
%表中34个城市的位置坐标保存在citys_data1.mat文件中,变量citys为34行2列的
%数据,第1列表示城市的横坐标,第2列表示城市的纵坐标。
load citys_data.mat%% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endend
end%% 初始化参数
m = 35; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度 %% 迭代寻找最佳路径
while iter <= iter_max% 随机产生各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start; % 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha ...* Eta(tabu(end),allow(k))^beta;endP = P/sum(P);% 轮盘赌法选择下一个访问城市Pc = cumsum(P); target_index = find(Pc >= rand); target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length; Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = ...Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);endDelta_Tau(Table(i,n),Table(i,1)) = ...Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1,清空路径记录表iter = iter + 1;Table = zeros(m,n);
end%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),...citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
结果分析:
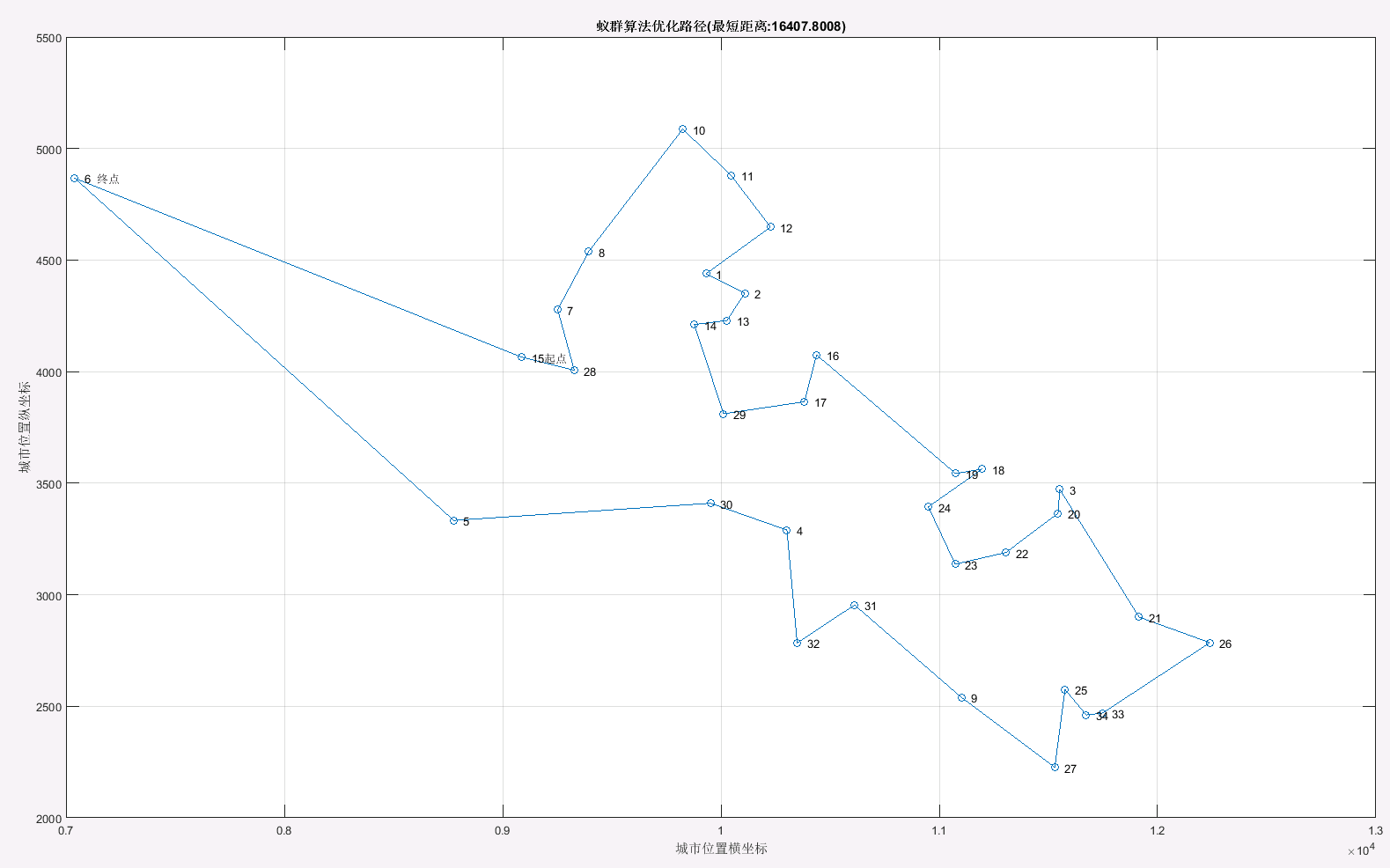
从上图中可以清晰地看到,自起点出发,每个城市访问一次,遍历所有城市后,返回起点。寻找到的最短距离为16407.8008公里。最短路径为15,28,7,8,10,11,12,1,2,13,14,29,17,16,19,18,24,23,22,20,3,21,26,33,34,25,27,9,31,32,4,30,5,6,15。
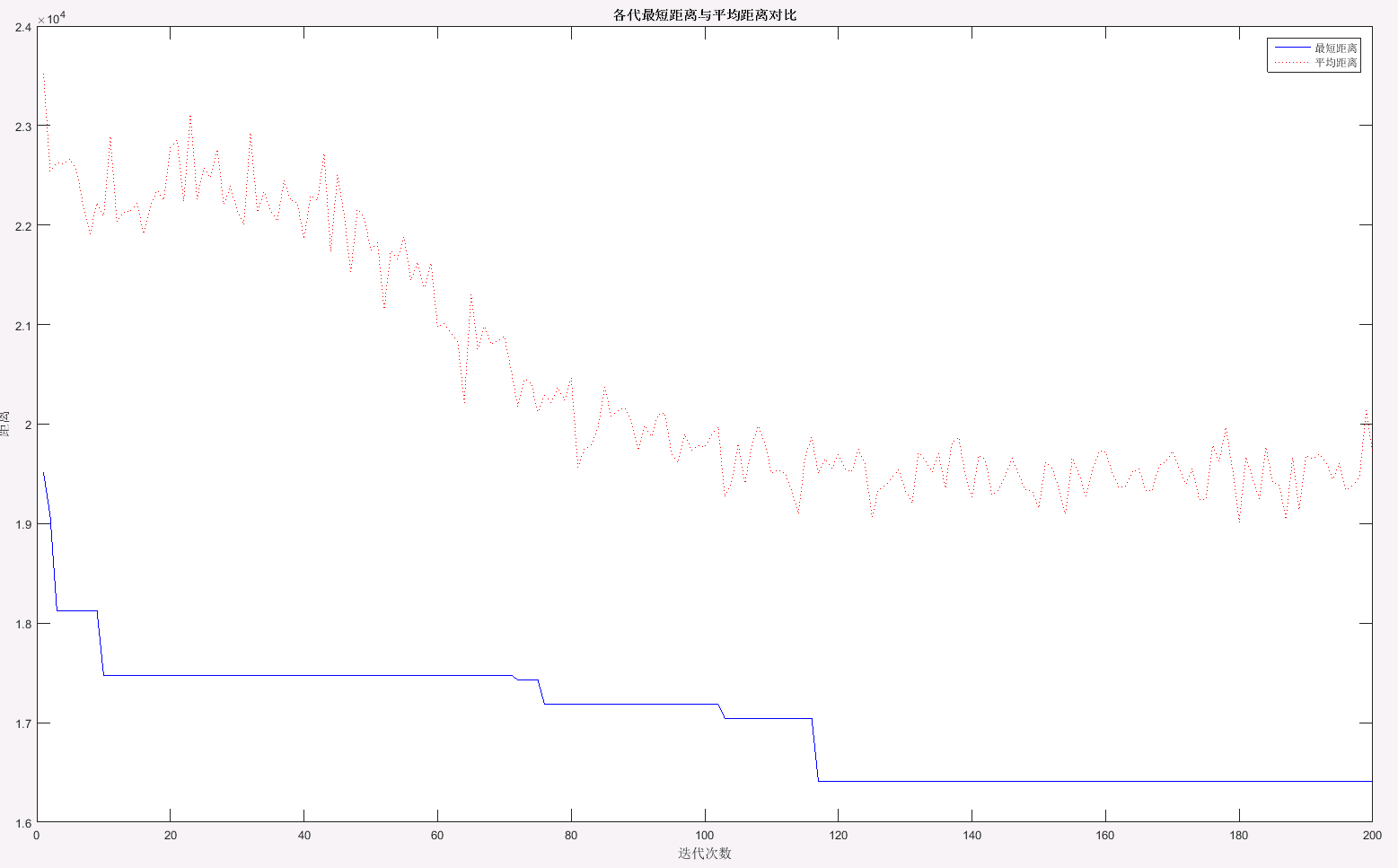
各代的最短距离与平均距离如上图所示,从图中不难发现,随着迭代次数的增加,最短距离与平均距离均呈现不断下降的趋势。当迭代次数大于116时,最短距离已不再变化,表示已经寻找到最佳路径。
四. 练习
张三学习了蚁群算法之后特别高兴,他定义了一个特别的图,希望找到图中的最短路径。
张三的图由 2021 个结点组成,依次编号 1 至 2021。
对于两个不同的结点 aaa,bbb,如果 aaa 和 bbb 的差的绝对值大于 21,则两个结点之间没有边相连;如果 aaa 和 bbb 的差的绝对值小于等于 21,则两个点之间有一条 长度为 aaa 和 bbb 的最小公倍数的无向边相连。
例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为 75。
利用蚁群算法确定最短的巡回路径,以及从结点 1 到结点 2021 之间的最短路径长度是多少。
相关文章:

RPC-原理及RPC实例分析
还有就是:RPC支持的BIO,NIO的理解 (1)BIO: Blocking IO;同步阻塞; (2)NIO:Non-Blocking IO, 同步非阻塞; 参考:IO多路复用,同步,异步,阻塞和非阻塞 区别 在学校期间大家都写过不少程序,比如写个…

hdu 4608 I-number
http://acm.hdu.edu.cn/showproblem.php?pid4608 直接暴力 代码: #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<set> #include<map> #include<stack> #inc…

php tab标签,JavaScript代码分享:tab标签的切换
本文实例讲述了js实现点击切换TAB标签。分享给大家供大家参考。具体如下:这里演示的选项卡效果代码,无jq,纯JS来实现,灰色风格,没有怎么美化,或许看上去比较普通,不过兼容性和操作起来挺舒服的,…

二进制,十进制,十六进制
生活中其实很多地方的计数方法都多少有点不同进制的影子。 比如我们最常用的10进制,其实起源于人有10个指头。如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。 至于二进制……没有袜子称为0只袜子,有一只袜子称为…

D3.js系列——初步使用、选择元素与绑定数据
D3 的全称是(Data-Driven Documents),顾名思义可以知道是一个被数据驱动的文档。听名字有点抽象,说简单一点,其实就是一个 JavaScript 的函数库,使用它主要是用来做数据可视化的。 D3 提供了各种简单易用的…

秦州:西瓜书 + 南瓜书 吃瓜系列 12. 聚类
Datawhale南瓜书是经典机器学习教材《机器学习》(西瓜书)的公式推导解析指南,旨在让在学习西瓜书的过程中,再也没有难推的公式,学好机器学习。 航路开辟者:谢文睿、秦州开源内容:https://githu…

php 5/0,PHP 5.5.0 released.该怎么解决
当前位置:我的异常网 PHP PHP 5.5.0 released.该怎么解决PHP 5.5.0 released.该怎么解决www.myexceptions.net 网友分享于:2013-08-02 浏览:12次PHP 5.5.0 released.The PHP development team is proud to announce the immediate availability of PH…

Windows下SVN权限配置过程详解
本节讲解一下Windows下SVN权限配置说明,针对的是一个目录下多库的情况,下面是具体的介绍,希望通过本文的学习,你能够对SVN权限配置问题有更加深刻的认识。 1、本文档适用于对Subvesion的自带服务svnserve进行权限配置,…

胡小明:大数据应用方向思考
一、警惕大数据过热 1.1 过热产生盲目性 国内大数据的宣传早已过热,很多区县级政府也在考虑成立大数据局,政府对大数据热几乎没有抵抗力,企业没有紧跟就对了,在大数据高潮中反省政府的大数据行为、冷静一下头脑是有益的࿰…
Datawhale组队学习周报(第040周)
本周报总结了从 11月15日至11月21日,Datawhale组队学习的运行情况,我们一直秉承“与学习者一起成长的理念”,希望这个活动能够让更多的学习者受益。 第 31 期组队学习已经与大家见面了,这次组队学习一共 11 门开源课程࿰…

matlab 无序数对,MATLAB中sort函数对矩阵数进行排序
(1)Bsort(A) 对一维或二维数组进行升序排序,并返回排序后的数组,当A为二维时,对数组每一列进行排序.eg: A[1,5,3],则sort(A)[1,3,5]A[1,5,3;2,4,1],则sort(A)[1,4,1;2,5,3](2)Bsort(A,dim),对数组按指定方向进行升序排序,dim 1,表示对每一列进行排序,,dim2表示对每一行进行排序…

云智易获上海CIO联盟“年度物联网云平台技术创新奖”
6月23日,云智易作为国内领先物联网云平台,受邀出席“跨界融合 聚势谋远”上海CIO联盟峰会。本次大会汇聚了全球各地各行业300位精英翘楚,共话未来发展趋势。 在本次大会中,云智易物联云平台凭借强大的技术实力、成熟的平台架构、…

d3d导致cairo不正常
最近要把cairo集成到项目中,却发现cairo不能工作了 折腾了两天才找到了原因:cairo的一个trick导致浮点数计算错误: http://blog.163.com/lvan100yeah/blog/static/6811721420131191434556/ 给d3dcreate加上D3DCREATE_FPU_PRESERVE之后一切正常 如果我直接调cairo的代码就能早点…

青少年编程竞赛交流群周报(第038周)
2021年11月21日(周日)晚20:00我们在青少年编程竞赛交流群开展了第三十八期直播活动。 一、直播内容 我们直播活动的主要内容如下: 讲解了上次测试中小朋友们做错的题目 Scratch青少年编程能力等级测试模拟题(四级)。…

php的遍历方法,PHP数组遍历方法总结
在PHP中数组分为两类: 数字索引数组和关联数组。其中数字索引数组和C语言中的数组一样,下标是为0,1,2…而关联数组下标可能是任意类型,与其它语言中的hash,map等结构相似。下面介绍PHP中遍历关联数组的三种…

二、Silverlight中使用MVVM(二)——提高
在第一篇文章中的示例中,我们已经简单的了解了应用MVVM模式的流程,我的本意是你已经了解了一点MVVM的概念,然后又没有一个较好的例子学习,可以跟着我一起学习MVVM模式,所以这个部分,都是没有理论知识的&…

中国电子学会青少年编程能力等级测试图形化四级编程题:太空大战
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

Pycharm开发环境设置与熟悉。
练习基本输入输出: print(你好,{}..format(name)) print(sys.argv) 库的使用方法: import ... from ... import ... 条件语句: if (abs(pos()))<1: break 循环语句: for i in range(5): while True: 函数定义: def …

oracle 默认表空间 10g,Oracle10g 表空间管理
1.表空间分类:(1)临时表空间:存放临时数据(2)数据表空间:又称为用户表空间,用来存放永久数据(不删除永久存在)(3)日志表空间:用来存放日志信息一般情况下,用户使用时只需要创建数据表空间即可,根…

POJ1022 Packing Unit 4D Cubes
题目来源:http://poj.org/problem?id1022 题目大意: 有一些4维的单位体积的立方体盒子,每个立方体有8个面。要用一个大的4为盒子将它们包起来,求最小的大盒子体积。 输入:第一行为测试用例数。每个用例的第一行为单位…

中国电子学会青少年编程能力等级测试图形化三级编程题:海底寻宝
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

用Ajax请求服务器的图片,并显示在浏览器中(转)
前言 一直在数据库里面存的都是图片在服务器的地址,然后再到浏览器中显示,但是发现两个问题 第一:为了安全起见,js是无法读取本地的图片的,不然你写一个js,岂不是可以获取任何人电脑里面的文件了。 第二&am…

pb设置Oracle事务的隔离级别,Oracle的事务隔离级别
ANSI/ISO SQL规定了四种事务隔离级别,分别是:read uncommitted,read committed,repeatable read,serializableORACE提供了SQ92标准中的read committed和seriaizabe,同时提供了非SQ92标准的read-ony。read committed:这是ORACE缺省…

inux php pdo mysql 扩展
今天在本机部署了一个pdo项目,发现一些问题,真没想到pdo mysql,不容易装啊,哈哈,我说的不容易,是因为php5.3以前版本,yum源里面根本没有。部署后就报,Undefined class constant MYSQ…

Maven项目Spring Boot启动
1. pom.xml中增加配置 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.0.0.RELEASE</version></parent><dependencies><dependency><gr…

中国电子学会青少年编程能力等级测试图形化四级模拟题
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

Oracle设置date数据比较,ORACLE DATE和TIMESTAMP数据类型的比较
DATE数据类型这个数据类型我们实在是太熟悉了,当我们需要表示日期和时间的话都会想到date类型。它可以存储月,年,日,世纪,时,分和秒。它典型地用来表示什 么时候事情已经发生或将要发生。DATE数据类型的问题…

POJ 1552 Doubles (C++ STL set使用)
题目: 题意:题意:给出几个正数(2~15个),然后就是求有这些数字的2倍有没有和原先的正数相同的,求出有几个,没有就是0. 分析:水题。用数组解决,开一个数组存正数…

凌亮:动手学数据分析笔记
凌亮是华北电力大学数理系大二的学生,LSGO软件技术团队(Dreamtech算法组)成员,参加了多期Datawhale的组队学习。 这篇图文是他在线下组队学习时,为大家分享自己学习“动手学数据分析”的笔记。 希望参与我们线下组队…

【H.264/AVC视频编解码技术详解】十九:熵编码算法(5)——H.264的CABAC(上):语法元素的二值化方法...
《H.264/AVC视频编解码技术详解》视频教程已经在“CSDN学院”上线,视频中详述了H.264的背景、标准协议和实现,并通过一个实战工程的形式对H.264的标准进行解析和实现,欢迎观看! “纸上得来终觉浅,绝知此事要躬行”&…
