邻域数、直接密度可达、密度可达、密度相连的概念


例子:如图所示,Eps用一个相应的半径表示,设MinPts=3,请分析Q,M,P,S,O,R这5个样本点之间的关系。

易知,P,M,Q,O,SO之间的点,OR之间的点都是核心点
M是从P直接密度可达,Q是从M直接密度可达
Q是从P密度可达(反之不是),S是从O密度可达,R是从O密度可达
S和R密度相连
注意:
①
直接密度可达和密度可达是不对称的,
即A从B密度可达未必B从A密度可达。
密度相连是对称的,
因而可以说A和B密度相连。
②
密度可达建立在直接密度可达的基础上
这就要求判断那些中间介质点是否是核心点
相关文章:

VUE中使用Echarts绘制地图迁移
踩坑说明 很久以前写jsp时使用过echarts的china.js插件,不过echarts是2.0的,目前vue项目中使用echarts3.8.5,直接将china.js插件引入,代码复制,运行一看,GG。地图中央只有一个光溜溜的南海群岛框框…

关于mysql字符集及导入导出
MySQL字符集设置 • 系统变量:– character_set_server:默认的内部操作字符集– character_set_client:客户端来源数据使用的字符集– character_set_connection:连接层字符集– character_set_results:查询结果字符集…

javascrip 常用属性
1 隐藏控件<div style"dispay:none"><asp:TextBox id"txthiddent" run"server"></asp:TextBox></div>2 页面引用带的<script> </script> EnDate.JS<head><!--#Include File"Js/EnDate.js&q…

数据预处理知识点汇总
(一) 数据清理 a) 缺失值填充 i. 忽略元组 ii. 手工填写 iii. 自动填充 使用属性均值推理出最可能的值,如贝叶斯公式或决策树 b) 去除离群点 i. 聚类 ii. LOF iii. 回归函数拟合数据 c) 噪音(包括错误和离群)处理 i. 分箱光滑 d) 纠正不一致数据 (二) …

Android支付接入(五):机锋网
前边已经陆续跟大家走了一遍运营商和支付宝付费接入,今天跟大家一起看看机锋网的支付接入。事实上付费接入本身并没有太多须要注意的地方,做的多了以后你会发现套路都是大同小异的。而须要注意的地方在于怎么跟游戏兼容及后期的维护,包含增减…

腾讯广告广点通API接入文档(Android)
官方文档地址 如果能够看懂文档的也没有必要再往下面看了。本篇文章就到此结束。 下面记录的是本人在上面锁踩过的坑,因为我发现Mac电脑上面的联系客服不是我想要的。 本来只是内部使用的文档,后来想想还是公开出来,希望能够帮助到人。进入正…

Linux下的下载工具 axel
下载地址:http://wilmer.gaast.net/main.php/axel.html Axel是命令行下的多线程下载工具,支持断点续传,速度通常情况下是Wget的几倍。 下载后使用如下命令编译安装: #tar zxvf axel-1.0a.tar.gz #cd axel-1.0a/ #./con…

集成学习知识点汇总
为啥叫集成学习 结合多个学习器来完成学习任务。 俗话说就是,团结力量大。 个体学习器可以相同可以不同。如果相同叫同质集成,如果不尽相同叫异质集成。 个体学习器最好满足:好而不同。 所谓好(准确性),就是个体学习器不能太坏&…

hdu 2028 Lowest Common Multiple Plus
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid2028 题目大意:求最小公倍数,用辗转相除法。 1 #include <stdio.h>2 int main ()3 {4 int gcd(int a,int b);5 int a,b,n,i,c;6 while (scanf("%d",&n)…

TreeView
6.遍历TreeView节点(递归算法) private void Page_Load(object sender, System.EventArgs e) { GetAllNodeText(TreeView1.Nodes); } void GetAllNodeText(TreeNodeCollection tnc) { foreach(TreeNode node in tnc) { if(node.Nodes.Count!0) GetAllNodeText(node.Nodes); Res…

FZU 2297 Number theory【线段树/单点更新/思维】
Given a integers x 1, you have to apply Q (Q ≤ 100000) operations: Multiply, Divide. Input First line of the input file contains an integer T(0 < T ≤ 10) that indicates how many cases of inputs are there. The description of each case is given below: …
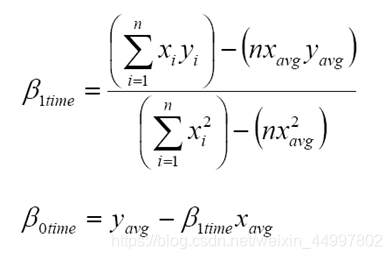
<软件过程与改进>计算大题考点总结与例题
1.PSP_PROBE估算法 常见考法:给历史数据,需要选择代理规模的估算值和程序规模/所需资源的实际值,用以下公式求得拟合公式参数 然后使用公式计算出未知的程序规模/所需资源 例题 2.PSP过程质量的度量指标_yield 常见考法:给出缺…

c语言exit和return区别,在fork和vfork中使用
转自c语言exit和return区别,在fork和vfork中使用 exit函数在头文件stdlib.h中。 简述: exit(0):正常运行程序并退出程序; exit(1):非正常运行导致退出程序; r…

WIKI与BLOG殊途同归(转)
现在很多朋友都拥有了自己的BLOG网页,尽管他们可能并不打算走木子美那种写私人日记的路子,但彰显个性、张扬自我的目的,大都类似。其实在这个时候,中国的许多技术迷们已经把目光投向了WIKI。 历经了网络反黄与木子美,中…

Spring MVC中DispatcherServlet理解总结(1)
DispatcherServlet在web.xml中的配置 <context-param><!--默认配置文件为/WEB-INF/[servlet名字]-servlet.xml--><param-name>contextConfigLocation</param-name><param-value>WebApplicationContext的上下文配置</param-value> </con…
功能点度量方法介绍
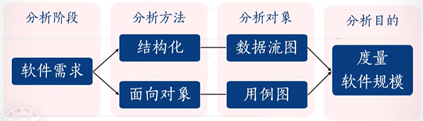
功能点度量方法是利用软件需求分析度量软件规模。 软件需求分析包括:软件功能需求分析、软件性能需求分析 在需求分析阶段可以利用数据流图和用例图对软件规模进行度量,分别对应功能点度量与用例点度量方法 1.功能点度量方法的分类 第三种 IFPUG是我…

微软2014校园招聘笔试试题
转载请标明出处,原文地址:http://blog.csdn.net/hackbuteer1/article/details/121908071、Which statement(s) is(are) correct about thread and process?Select all that apply.(5 Points) A、Threads share the same address space of the…

vi(vim)快捷键小记
1、前言 vi是“visual interface”的缩写,vim是vi IMproved(增强版的vi)。总结一下自己平时常用的vim快捷键,当是忘记也好,后续会不定期更新。 2、vim 快捷键 快捷键说明vi[m] file打开[新建]文件命令模式可以移动光标、删除字符等h,j,k,l左…
Premiere Pro2.0用DebugMode2.3搭桥小日本4.0输出图解
看图说话,不懂的多试试看首先明确几点:1。3个软件:Premiere Pro2.0、DebugMode(帧服务器)、小日本(TMPGEnc 4.0 XPress)2。渲染过程是在小日本中完成,与DebugMode无关,De…

用例点度量方法介绍
用例点度量方法分为6个步骤,分别是 step 1:计算未调整前的角色(执行者)权重 将角色按照复杂程度分为3类,具体如下 则本例中 UAW1121329 计算未调整前的用例权重UUC 有三种评估用例复杂程度的方法,具体如下 以下是用例权重评估表(普通那…

NYOJ——街区最短路径问题
街区最短路径问题 时间限制:3000 ms | 内存限制:65535 KB难度:4描述一个街区有很多住户,街区的街道只能为东西、南北两种方向。住户只可以沿着街道行走。各个街道之间的间隔相等。用(x,y)来表示住户坐在的街区。例如(…

Git 中常用的 4 个命令
使用 Git 进行版本管理时,肯定不只做提交,有时候也会需要回退修改,并且在回退的基础上进行重新提交,这时候有几个常用的命令就需要用到了,下面分别做介绍。 1、查看提交日志 首先,我们查看当前提交记录的命…

7月17日 晴
小懒猫,太阳晒PP拉Mua转载于:https://www.cnblogs.com/loverain/archive/2008/07/17/1244992.html

AS更改初始布局遇到的问题
将所有的simple.xml.ftl的内容都改成 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"…

android Json解析详解
JSON的定义: 一种轻量级的数据交换格式,具有良好的可读和便于快速编写的特性。业内主流技术为其提供了完整的解决方案(有点类似于正则表达式 ,获得了当今大部分语 言的支持),从而可以在不同平台间进行数据交…
[二]Java虚拟机 jvm内存结构 运行时数据内存 class文件与jvm内存结构的映射 jvm数据类型 虚拟机栈 方法区 堆 含义...
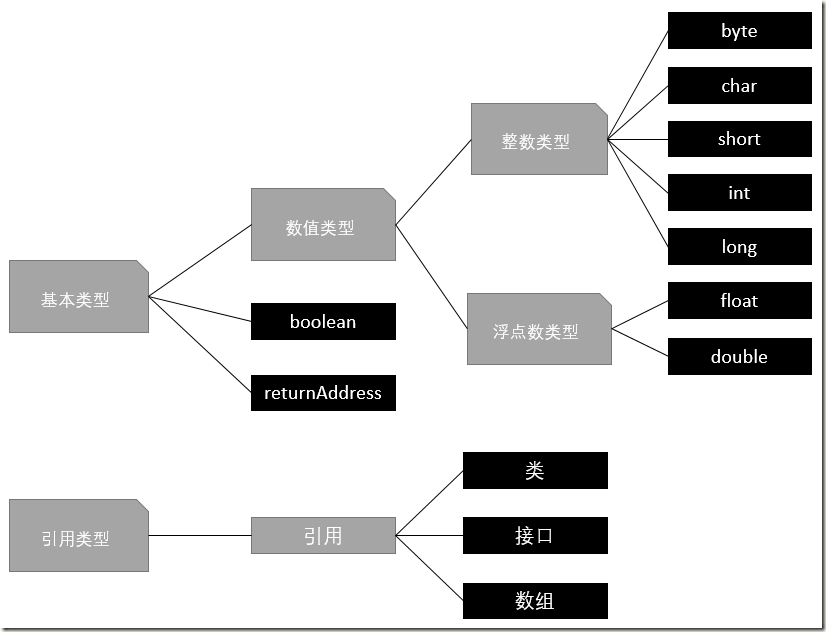
前言简介 class文件是源代码经过编译后的一种平台中立的格式 里面包含了虚拟机运行所需要的所有信息,相当于 JVM的机器语言 JVM全称是Java Virtual Machine ,既然是虚拟机,他终归要运行在物理机上 在操作系统中体现出来的也就是一个进程 操作系统会给他分配资源,割一块内存作为…

import android.support.v7.widget.RecyclerView失败
换成 androidx.recyclerview.widget.RecyclerView 参考文章 https://blog.csdn.net/u013183608/article/details/89428611/
CrackMe_001
本系列文章的目的是从一个没有任何经验的新手的角度(其实就是我自己),一步步尝试将160个CrackMe全部破解,如果可以,通过任何方式写出一个类似于注册机的东西。 其中,文章中按照如下逻辑编排(解决如下问题)&…

用javascript实现的纵版飞行射击游戏—《天机》
花了一个半月的时间用javascript完成了这款web版飞行射击游戏,游戏效果接近一般的客户端游戏,不过对机器的要求稍微高点点,主要是CPU,最好在1.5GHZ以上,不然可能会比较卡,支持IE、FF、Opera、safari。 用ja…

对分组交换(packet switching)高效迅速灵活可靠四个优点的理解
1.什么是分组? 通信过程中要发送的整块数据被称为一个报文(message),报文被划分为一个个更小的等长数据段,每个数据段前加入一些由必要的控制信息组成的首部后,就构成了一个分组。分组是在互联网中传送的数据单元(长报文ÿ…
