实对称矩阵的性质_浅谈矩阵的相似对角化(一)


通过前面的讨论,我们引出了线性变换在不同基下的矩阵之间的关系,知道了线性变换在不同基下的矩阵是相似的,进而我们可以通过选取不同的基,使得线性变换在这组基下的矩阵的形式最简单,由于对角矩阵具有良好的性质,因此我们希望通过选取合适的基,使得线性变换在这组基下的矩阵是对角矩阵,这个问题等价于寻找一个可逆矩阵
设
其中
于是
设线性变换
则
故
即
因为
对上式移项并提公因式得
下面要证明不同特征值对应的特征向量是线性无关的:
设
由
由
令
因为
由于
同理,
综上
故
现在我们讨论怎样寻找可逆矩阵
即
假设我们已经找到可逆矩阵
将矩阵
则有
即
若
则有
即当n阶矩阵
反过来,若
假设
则线性变换
即
则有
故
综上,矩阵
由于我们之前证明了不同特征值对应的特征向量是线性无关的,因此若矩阵
在下一篇文章里面我们将讨论实对称矩阵的相似对角化问题以及二次型的标准化问题。
未完待续...
相关文章:

区块链技术未来可能用于哪些方面?
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 当世界上从100比特币购买25美分的比萨饼,到一比特币兑换4800人民币的天价,在这风起云涌的纪念,我们见证了一个…

tomcat启动
tomcat的启动一般是从startup.bat/startup.sh开始,然后启动catalina.bat/catalina.sh,然后启动bootstrap.jar包 那么它们启动的时候都做了哪些事情呢? 首先是startup.bat,startup.bat做了什么? 第二是catalina.bat&…
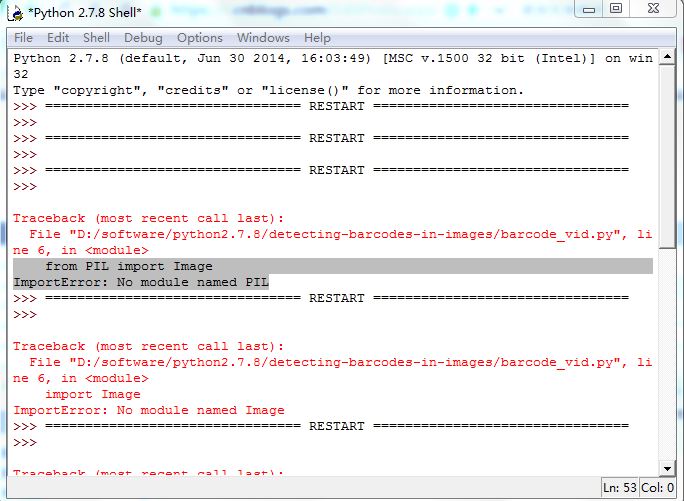
ERROR: from PIL import Image ImportError: No module named PIL
ERROR: from PIL import Image ImportError: No module named PIL 到 http://www.pythonware.com/products/pil/ 下载相关支持的版本 我的是python2.7 直接打开,然后一路按“下一步”,就行 转载于:https://www.cnblogs.com/jakejian/p/8992…

python中font_Python ColorFont包_程序模块 - PyPI - Python中文网
控制台打印彩色字体0 黑色 8 灰色1 蓝色 9 淡蓝色2 绿色 A 淡绿色3 浅绿色 B 淡浅绿色4 红色 C 淡红色5 紫色 D 淡紫色6 黄色 E 淡黄色7 白色 F 亮白色格式:0x12高位代表背景色,低位代表字体颜色0x10 | 0x020x10代表背景色,0…

区块链技术到底有啥用?
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 前言:关于区块链适合做什么和不适合做什么?一直都有争议。那么,通过什么方式来辨别呢?本文用详细的…
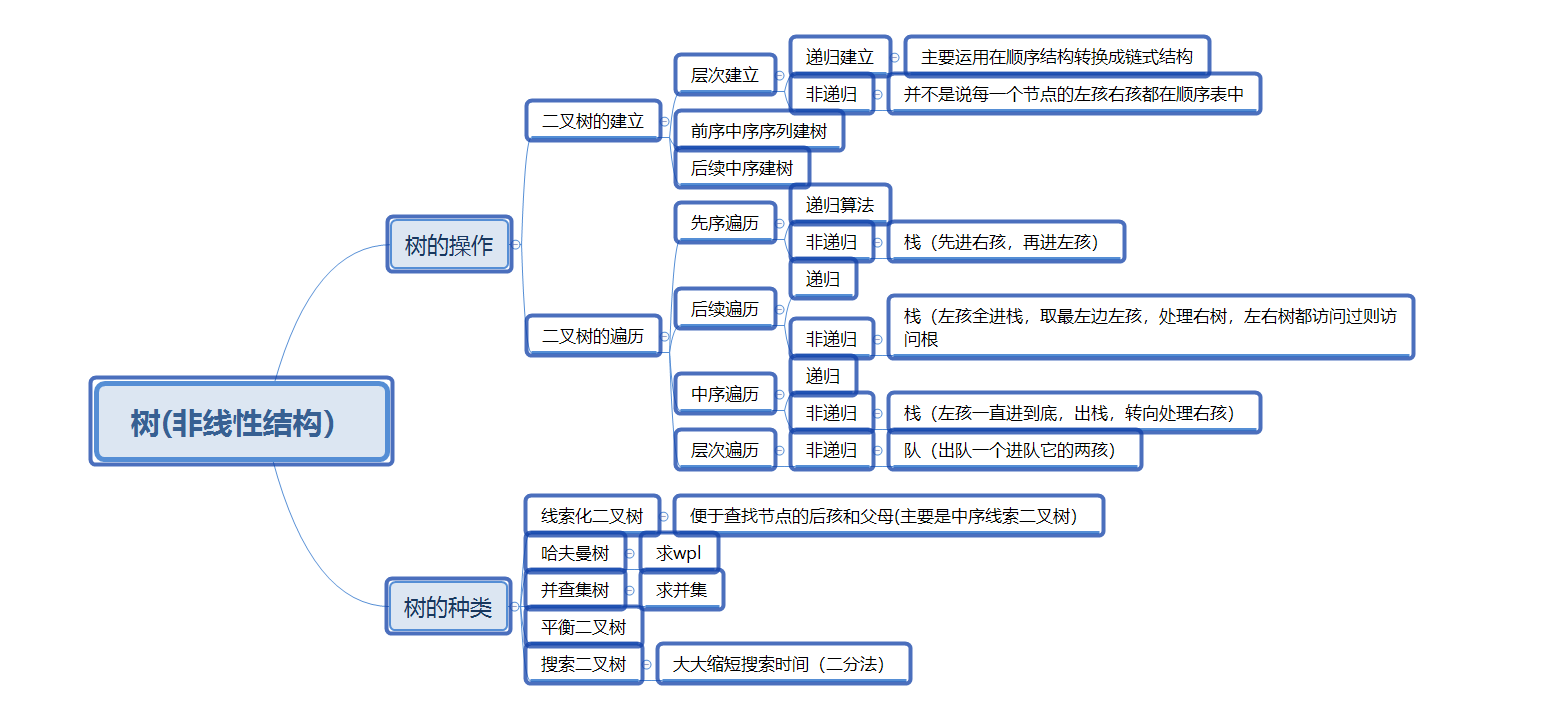
博客作业04--树
一.学习总结(2分) 1.1树结构思维导图 1.2 树结构学习体会 树的前中后序递归操作的访问路径都如下图 树的层次遍历的路径则如下图 操作{ 进队第一个节点, while(队不空) { 访问该节点, if(BT->lchild!NULL)进队。 if…
oracle数据如何获取游标中动态字段_如何实现报表数据的动态层次钻取(二)
上一篇《如何实现报表数据的动态层次钻取(一)》介绍了利用复杂 sql 实现动态层次结构的方法,但该方法依赖 Oracle 的递归语法,在其他类型的数据库中难以实现。要想通用地实现此类报表,可以使用下面介绍的“集算脚本 本…

使用jsonp跨域请求后可以获得数据,但是进入error方法,返回parseerror
$.ajax({ url:url, dataType:jsonp, jsonp: callback,//回调函数名字 jsonpCallback: success_jsonpCallback,//可以不写,也可以自定义,用来取代 jQuery 自动生成的随机函数名,不写将由jq自动生成,每次生成的结果都不…

EOS技术学习笔记
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 EOS.IO软件引入了一种新的块链架构,旨在实现分布式应用的性能扩展。这是通过创建一个可以构建应用程序的类似操作系统的架构来实现的。…

PHP的一种缓存方案静态化
1,解决的问题。 2.如何实现。 面对大流量网站频繁访问数据库的一种优化,比如博客网站。不可能每个人查看都访问一次数据库。为了解决大量不必要访问的问题。 可以把第一次的内容保存为html页面。再以后定义的过期时间内都访问该静态页面。 以下是一个小的demo index…

python获取机器唯一标识_开发中常用工具 - 获取设备的唯一标识、UDID、UUID、keychain保存UUID、判断网络...
UDID全名:Unique Device Identifie(设备唯一标识符)说明:UDID,即设备唯一标识符,这是除序列号之外每台iOS设备的独一无二的号码。UDID只是和设备相关的,是用来区分每一个唯一的iOS设备(包括iPhone、iPad等),…

区块链安全入门笔记
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 虽然有着越来越多的人参与到区块链的行业之中,然而由于很多人之前并没有接触过区块链,也没有相关的安全知识,安…

PHP程序员的技术成长规划
PHP程序员的技术成长规划 作者:黑夜路人(2014/10/15) 按照了解的很多PHP/LNMP程序员的发展轨迹,结合个人经验体会,抽象出很多程序员对未来的迷漫,特别对技术学习的盲目和慌乱,简单梳理了这个每个…

【资源共享】RK3288 WiFiBT 开发配置参考说明
本文档主要介绍RK3288平台的WiFi&BT配置说明。 下载地址:http://dev.t-firefly.com/thread-13642-1-1.html更多开发资料请到社区精华系列“资源共享”专栏下载http://dev.t-firefly.com/forum-263-1.html转载于:https://www.cnblogs.com/TeeFirefly/p/9001757.h…

软件工程实训有必要吗_人工智能专业值得读吗?就业如何?
要说这几年的风口,人工智能首当其冲。热门是否代表了好就业?我觉得不是;那是不是就不好就业?我觉得也不是。先来看看这些耸人听闻的标题吧——“人工智能人才缺口超过500万,补齐人才短板乃是当务之急“人工智能就业前景…

区块链共识算法:PoS即权益证明 DPoS委托授权的权益证明
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 随着比特币价格暴涨,基于比特币的区块链技术引起各方关注,其核心就是共识算法。随着区块链技术的发展共识算法也在不断创新与…

【洛谷P1697】货车运输
首先,对于所有从x能到达y的路径中,限重越大越好 因此我们用Kruskal最大生成树得到一片森林(不一定都联通) 之后dfs维护森林的深度和LCA的预处理limit[x][0](x向上跳2^i步的边权最小值) 对于每个询问&…

win7上Docker使用
1、启动docker: Docker Quickstart Terminal (快捷键)启动docker 2、SECURECRT工具链接docker: 转载于:https://www.cnblogs.com/aibaiyang/p/9007074.html

qt4的quick程序升级到qt5_最新8月书单出炉!送给你程序员
8月好书赏不停,喜欢的就收藏一下。1、计算广告:互联网商业变现的市场与技术(第2版)作者:刘鹏、王超全球第一本全面讲解计算广告与互联网变现秘密的专业图书升级版北冥乘海生 刘鹏老师力作&#…

都说区块链颠覆未来,区块链究竟能改变什么?
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 区块链,有时像个天使,有时像个魔鬼。 有人说它是金融泡沫,说他是彻底的庞氏骗局;有人说它能改变世界…

python银行家算法代码_避免死锁的银行家算法C++程序实现
本篇博文为追忆以前写过的算法系列第二篇(20081021)温故知新目的:具有代表性的死锁避免算法是Dijskstra给出的银行家算法。本实验是基于银行家算法的思想通过编写C程序实现银行家算法的计算机程序化。使其更有用。同一时候也加深了有关自愿…

shell脚本编程学习笔记(四)shell操作数据库
一、数据库基本操作 1)登录mysql服务器:mysql -u root -p 密码 2)查看数据库:show databases 3)查看表:show tales from db; 4)查看表结构:desc table; 5)创建表…

WebFrom模拟MVC
如: aspx前台 这样写生成页面时不会产生新的html标签,用控件则会产生新的html标签 <h1><% title %></h1> <p><% content %></p><ul> <% foreach (string item in list){%> <li>…

区块链的未来在哪里
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 经历了早期的野蛮成长之后,区块链行业的发展开始回归理性客观的发展阶段。探索区块链对于互联网行业的支持作用,而非颠覆作…
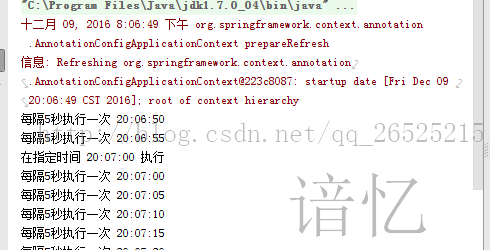
Spring注解之 @EnableScheduling计划任务注解
要实现计划任务,首先通过在配置类注解EnableScheduling来开启对计划任务的支持, 然后在要执行计划任务的方法上注解Scheduled,声明这是一个计划任务 示例:计划任务执行类 在这个类中的方法上需要Scheduled注解配合EnableSchedulin…

python爬虫案例_推荐上百个github上Python爬虫案例
现在学生都对爬虫感兴趣,这里发现一些好的github开源的代码,分享给各位1、awesome-spider 该网站提供了近上百个爬虫案例代码,这是ID为facert的一个知乎工程师开源的,star6000https://github.com/facert/awesome-spidergithub.c…

二元一次方程组
二元一次方程组(C语言) 学生:缪晓敏,施嘉依 #include <stdio.h>#include <math.h>int main() {double a1,b1,c1,a2,b2,c2,d,e,f;printf("a1 b1 c1 : ");scanf("%lf %lf %lf",&a1,&b1,&am…

超级账本(Hyperledger Fabric)源码分析之一:总览
链客,专为开发者而生,有问必答! 此文章来自区块链技术社区,未经允许拒绝转载。 一、编译 1、环境准备 需要提前在linux或者mac机器上安装如下软件 1)Go,注意设置好gopath(笔者安装的是go1.8…

建模与设计01
转载于:https://www.cnblogs.com/invisible2/p/9016732.html

Bzoj2110--Wc2011Xor
考虑如果我们已经到达了终点,那么从终点出发显然可以异或上图中任何地方一个环的异或值后再回到终点,那么我们显然可以在到达终点后根据环的异或值调整自己 所以我们可以先处理出环上的异或值,我的做法是先做一颗生成树,然后dfs确…
