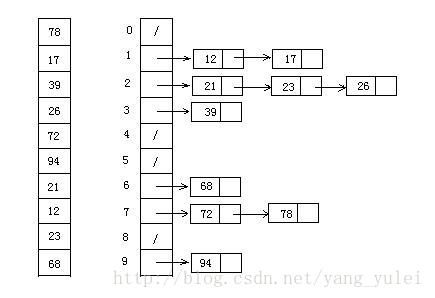
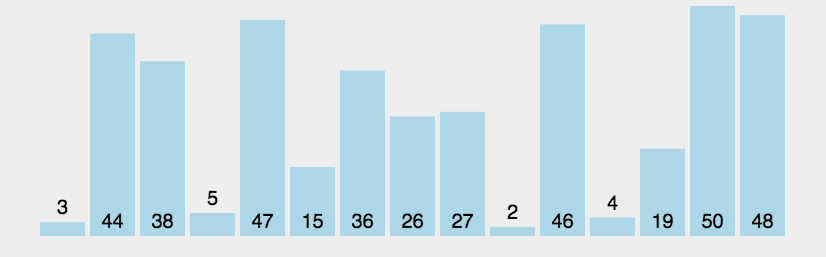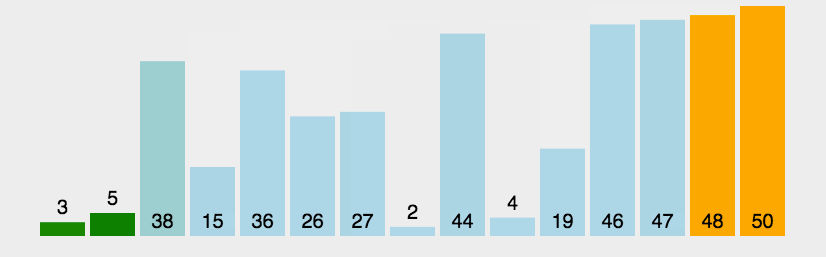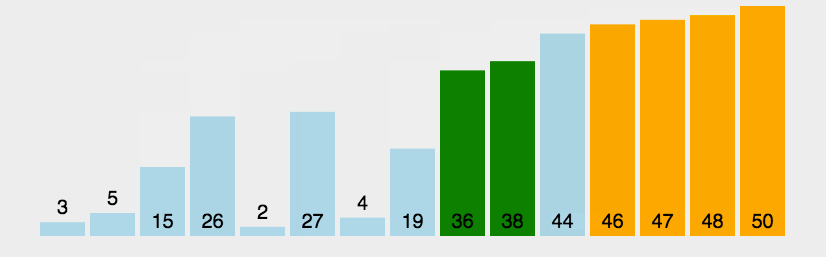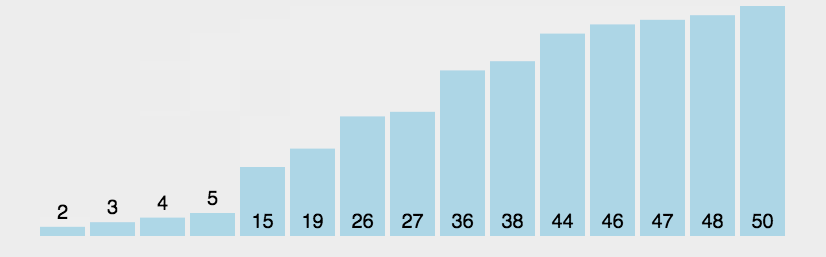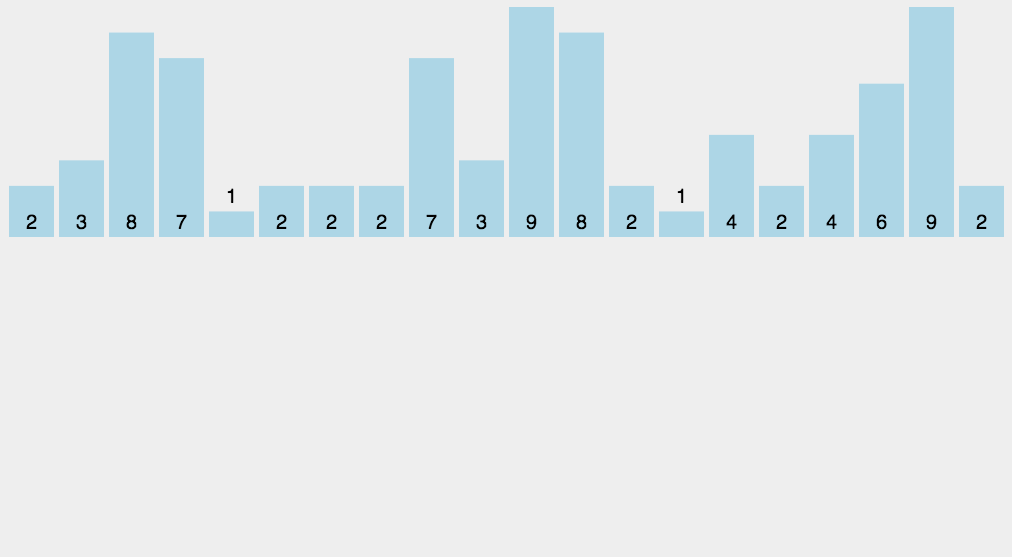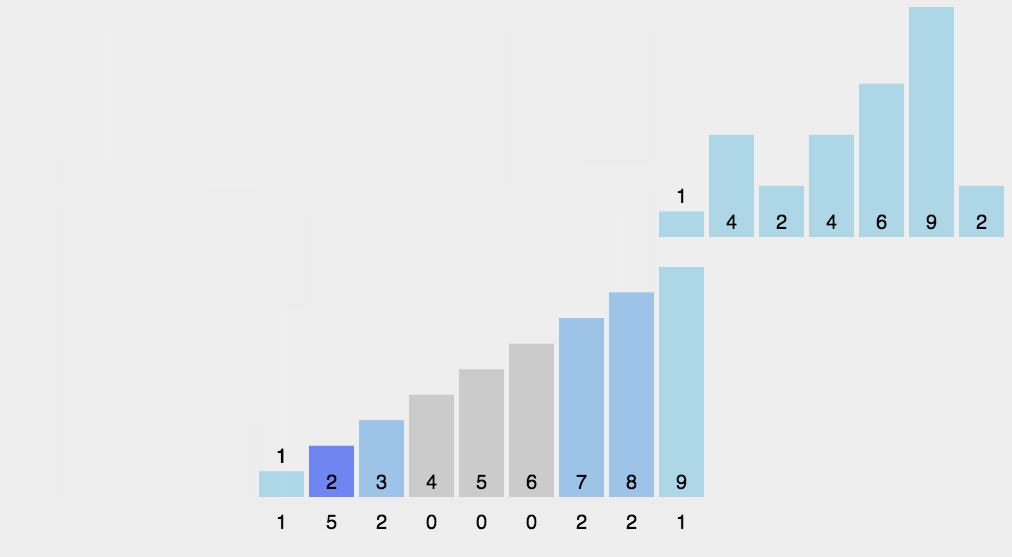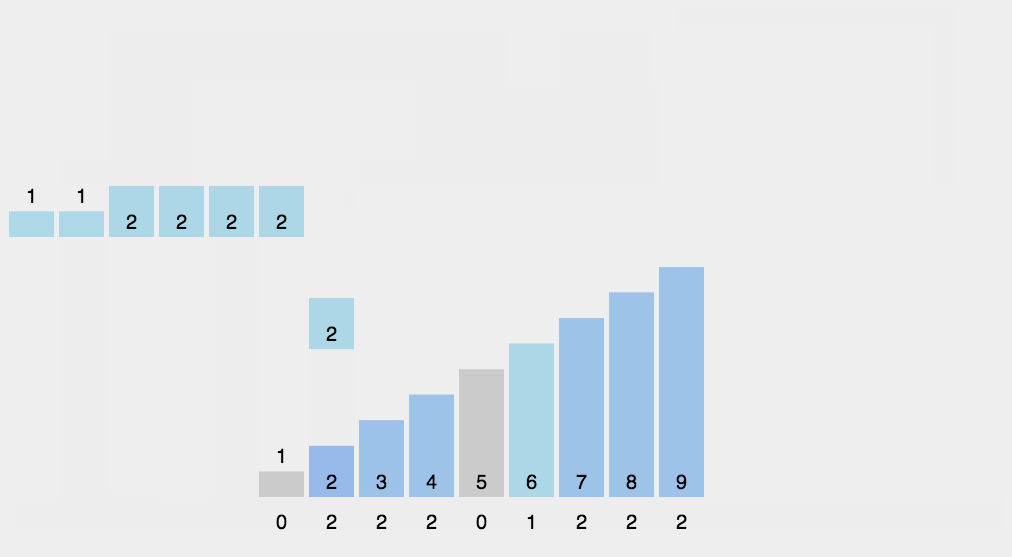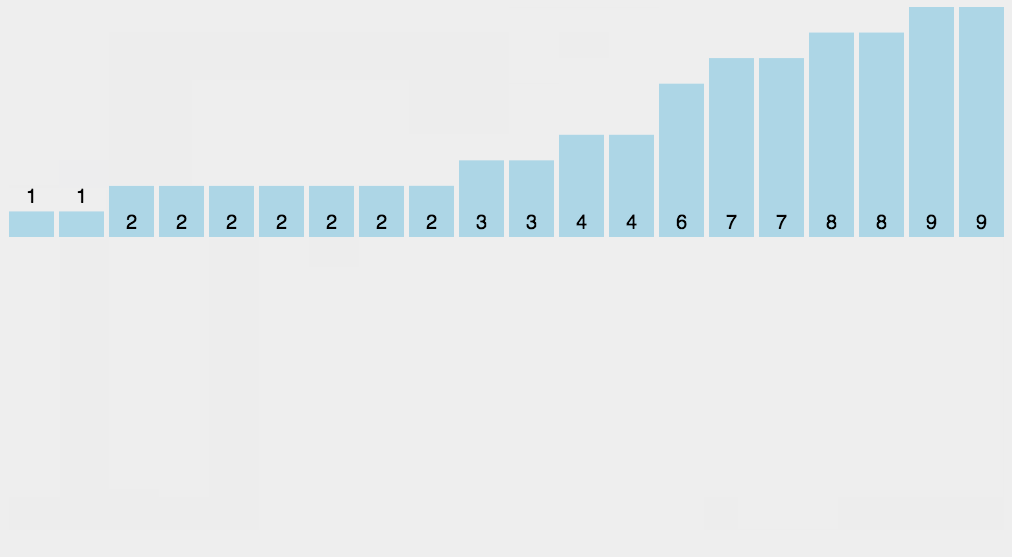十大算法,描述+代码+演示+分析+改进(赶紧收藏!)
十大算法
1.冒泡排序
(1)算法描述
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
(2)算法描述和实现
具体算法描述如下:
- <1>.比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- <2>.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- <3>.针对所有的元素重复以上的步骤,除了最后一个;
- <4>.重复步骤1~3,直到排序完成。
Java代码实现:
public static void bubbleSort(int[] array) {long start = System.nanoTime();int len = array.length;for (int i = 0; i < len - 1; i++) {for (int j = 0; j < len - i - 1; j++) {if (array[j] > array[j + 1]) {int tmp = array[j];array[j] = array[j + 1];array[j + 1] = tmp;}}}long end = System.nanoTime();System.out.println((end - start)/1000.0 + "ms");
}
改进冒泡排序: 设置一标志性变量pos,用于记录每趟排序中最后一次进行交换的位置。由于pos位置之后的记录均已交换到位,故在进行下一趟排序时只要扫描到pos位置即可。
改进后算法如下:
public static void bubbleSort2(int[] array) {long start = System.nanoTime();int len = array.length;int i = len - 1;while (i > 0) {int pos = 0;for (int j = 0; j < i; j++) {if (array[j] > array[j + 1]) {pos = j;int tmp = array[j];array[j] = array[j + 1];array[j + 1] = tmp;}}i = pos;}long end = System.nanoTime();System.out.println((end - start)/1000.0 + "ms");
}
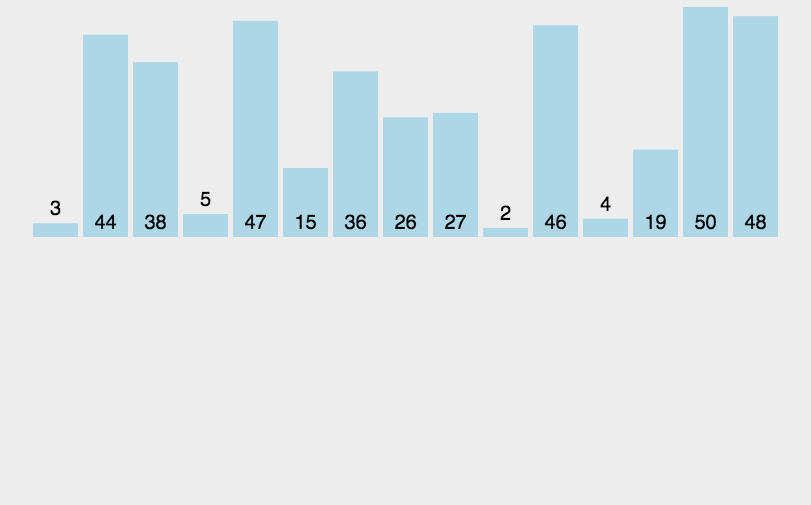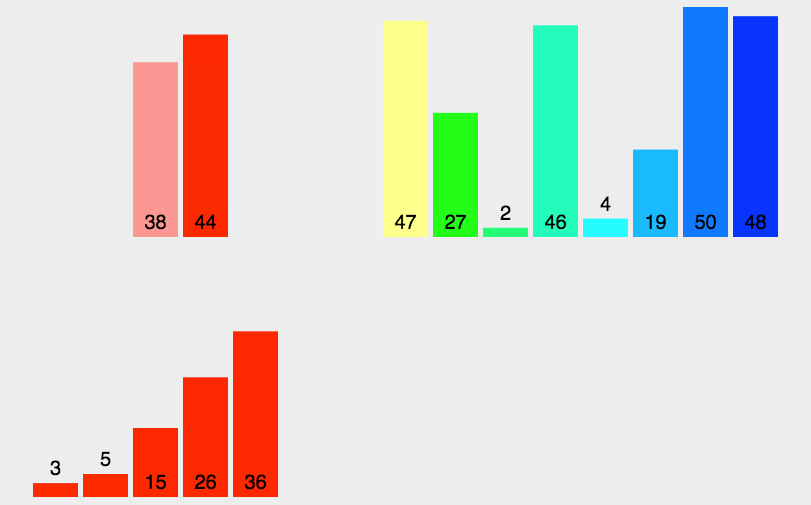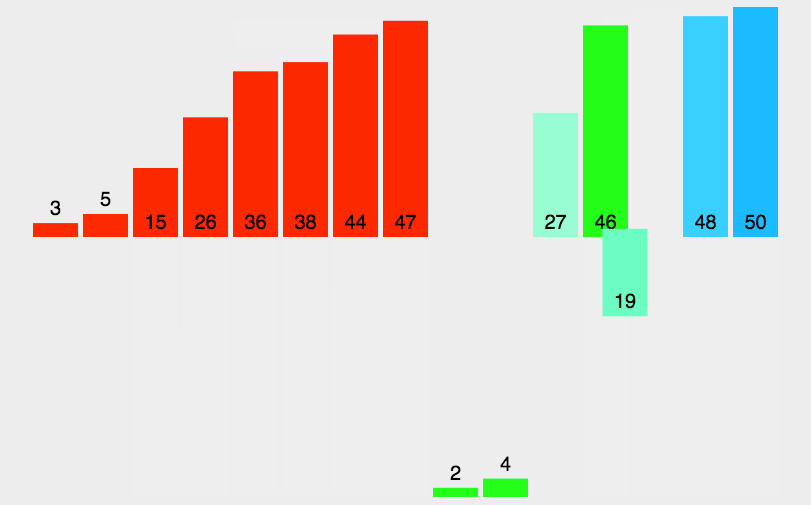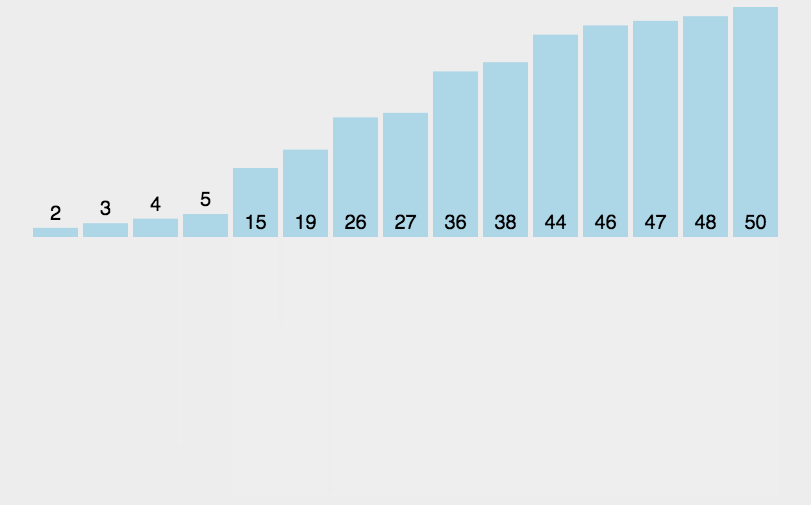
**冒泡排序动图演示
(3)算法分析
时间复杂度:
最佳情况:T(n) = O(n)
当输入的数据已经是正序时
最差情况:T(n) = O(n^2)
当输入的数据是反序时
平均情况:T(n) = O(n^2)
空间复杂度:
就空间复杂度而言,可以看到在每次循环中,所需要的额外空间就是在进行数值交换时候的一个额外空间,所以空间复杂度为一个常量O(1)
2.选择排序
表现最稳定的排序算法之一(这个稳定不是指算法层面上的稳定哈,相信聪明的你能明白我说的意思2333),因为无论什么数据进去都是O(n²)的时间复杂度……所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
(1)算法简介
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
(2)算法描述和实现
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
<1>.初始状态:无序区为R[1…n],有序区为空;
<2>.第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
<3>.n-1趟结束,数组有序化了。
Java代码实现:
public static void selectSort(int[] array) {long start = System.nanoTime();int len = array.length;int minIndex = 0;for(int i = 0; i < len - 1 ; i++) {minIndex = i;for(int j = i + 1; j < len; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}int tmp = array[minIndex];array[minIndex] = array[i];array[i] = tmp;}long end = System.nanoTime();System.out.println((end - start)/1000.0 + "ms");
}
选择排序动图演示:
(3)算法分析
时间复杂度:
最佳情况:T(n) = O(n^2)
最差情况:T(n) = O(n^2)
平均情况:T(n) = O(n^2)
空间复杂度:
同冒泡排序一样,占用常数的额外空间,所以空间复杂度为O(1)
3.插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。
(1)算法简介
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
(2)算法描述和实现
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
<1>.从第一个元素开始,该元素可以认为已经被排序;
<2>.取出下一个元素,在已经排序的元素序列中从后向前扫描;
<3>.如果该元素(已排序)大于新元素,将该元素移到下一位置;
<4>.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
<5>.将新元素插入到该位置后;
<6>.重复步骤2~5。
Java代码实现:
public static void insertSort(int[] array) {long start = System.nanoTime();int len = array.length;for (int i = 1; i < len; i++) {for (int j = i; j > 0 && array[j - 1] > array[j]; j--) {int tmp = array[j - 1];array[j - 1] = array[j];array[j] = tmp;}}long end = System.nanoTime();System.out.println((end - start) / 1000.0 + "ms");
}
改进插入排序: 查找插入位置时使用二分查找的方式。相比与上面简单插入排序,他针对每一批已排好序的序列,采用了二分查找的方式提高定位效率。
public static void insertSort2(int[] array) {long start = System.nanoTime();int len = array.length;for (int i = 1; i < len; i++) {int current = array[i];int st = 0;int en = i - 1;while (st <= en) {int mid = (st + en) >> 1;if (array[mid] < array[i]) {st = mid + 1;} else {en = mid - 1;}}for (int j = i - 1; j >= st; j--) {array[j + 1] = array[j];}array[st] = current;}long end = System.nanoTime();System.out.println((end - start) / 1000.0 + "ms");
}
插入排序动图演示:
(3)算法分析
最佳情况:输入数组按升序排列。T(n) = O(n)
最坏情况:输入数组按降序排列。T(n) = O(n^2)
平均情况:T(n) = O(n^2)
4.希尔排序
1959年Shell发明;
第一个突破O(n^2)的排序算法;是简单插入排序的改进版;它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序
(1)算法简介
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版》的合著者Robert Sedgewick提出的。
(2)算法描述和实现
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
<1>. 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
<2>.按增量序列个数k,对序列进行k 趟排序;
<3>.每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
Java代码实现:
public static void shellSort(int[] array) {long start = System.nanoTime();int len = array.length;int gap = len/2;//while(gap < len / 3) gap = 3 * gap + 1; //目前比较高效的gapwhile(gap >= 1){for(int i = gap; i < len; i++) {for(int j = i; j - gap > 0 && array[j - gap] > array[j]; j -= gap) {int tmp = array[j - gap];array[j - gap] = array[j];array[j] = tmp;}}gap /= 2;//gap /= 3;}long end = System.nanoTime();System.out.println((end - start) / 1000.0 + "ms");
}
希尔排序图示(图片来源网络):
(3)算法分析1959年Shell发明;
第一个突破O(n^2)的排序算法;是简单插入排序的改进版;它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序
(1)算法简介
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版》的合著者Robert Sedgewick提出的。
(2)算法描述和实现
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- <1>. 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- <2>.按增量序列个数k,对序列进行k 趟排序;
- <3>.每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
Java代码实现:
public static void shellSort(int[] array) { long start = System.nanoTime(); int len = array.length; int gap = len/2; //while(gap < len / 3) gap = 3 * gap + 1; //目前比较高效的gap while(gap >= 1){ for(int i = gap; i < len; i++) { for(int j = i; j - gap > 0 && array[j - gap] > array[j]; j -= gap) { int tmp = array[j - gap]; array[j - gap] = array[j]; array[j] = tmp; } } gap /= 2; //gap /= 3; } long end = System.nanoTime(); System.out.println((end - start) / 1000.0 + "ms"); }
希尔排序图示(图片来源网络):
(3)算法分析
- 最佳情况:T(n) = O(nlog2 n)
- 最坏情况:T(n) = O(nlog2 n)
- 平均情况:T(n) =O(nlog n)
最佳情况:T(n) = O(nlog2 n)
最坏情况:T(n) = O(nlog2 n)
平均情况:T(n) =O(nlog n)
5.归并排序
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
(1)算法简介
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
(2)算法描述和实现
具体算法描述如下:
<1>.把长度为n的输入序列分成两个长度为n/2的子序列;
<2>.对这两个子序列分别采用归并排序;
<3>.将两个排序好的子序列合并成一个最终的排序序列。
Java代码实现:
public static void mergeSort(int[] array, int start, int end) {int len = end - start + 1;if (len < 2) {return;}int middle = end + (start - end) / 2; //防止溢出mergeSort(array, start, middle);mergeSort(array, middle + 1, end);merge(array, start, end);
}private static void merge(int[] array, int start, int end) {int[] tmp = new int[end - start + 1];int mid = (start + end) / 2;int left = start;int right = mid + 1;int point = 0;while (left <= mid && right <= end) {if (array[left] < array[right]) {tmp[point++] = array[left++];} else {tmp[point++] = array[right++];}}while (left <= mid) {tmp[point++] = array[left++];}while (right <= end) {tmp[point++] = array[right++];}for (int i = 0; i < tmp.length; i++) {array[i + start] = tmp[i];}
}
归并排序动图演示:
(3)算法分析
最佳情况:T(n) = O(n)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
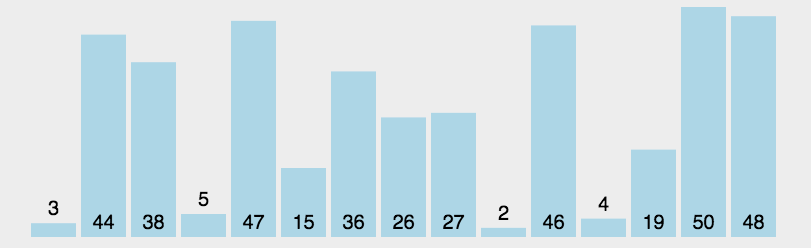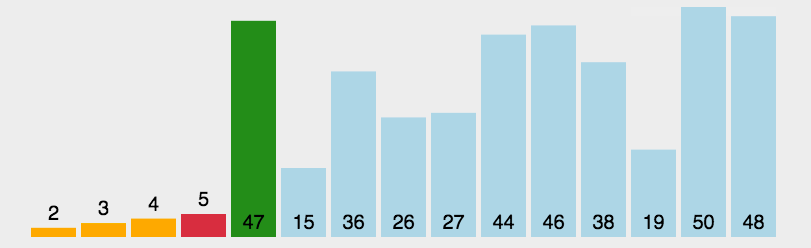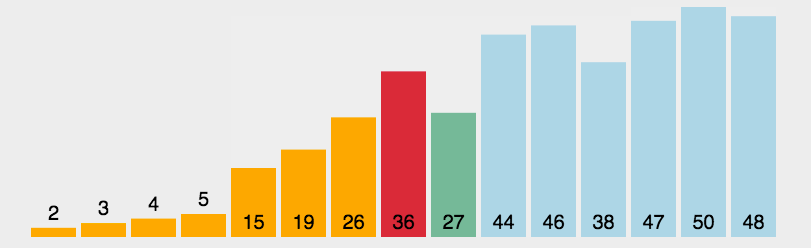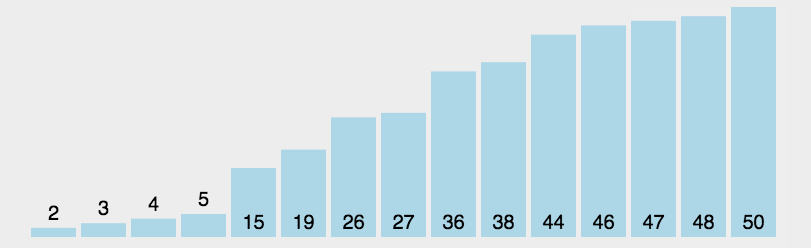
6.快速排序
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高! 它是处理大数据最快的排序算法之一了。
(1)算法简介
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
(2)算法描述和实现
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
<1>.从数列中挑出一个元素,称为 “基准”(pivot);
<2>.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
<3>.递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
Java代码实现:
public static void quickSort(int[] array, int st, int en) {int start = st;int end = en;if (start >= en)return;int index = partition(array, start, end);quickSort(array, st, index - 1);quickSort(array, index + 1, end);
}private static int partition(int[] array, int st, int en) {int reserve = array[st];int start = st;int end = en;if (start >= end)return start;while (start < end) {while (start < end && reserve <= array[end]) {end--;}if (start < end) {array[start++] = array[end];}while (start < end && array[start] <= reserve) {start++;}if (start < end) {array[end--] = array[start];}}array[start] = reserve;return start;
}快速排序动图演示:
快速排序算法优化——三向切分快速排序
在上面的快速排序中,当有很多重复元素存在的时候,会大大的增加无谓的切分耗时:比如当前切分块中若全部是相同的元素,则在当前块中的递归切分就是无意义也没有必要的。所以在三向切分中,用了lt和gt两个“指针”来分隔小于当前“基准元素”和大于当前“基准元素”的值。
public static void quickSort3ways(int[] array, int low, int high) {if (low >= high)return;int lt = low;int i = low + 1;int gt = high + 1;while (i < gt) {if (array[i] < array[lt]) {swap(array, i++, lt++);} else if (array[i] > array[lt]) {swap(array, i, --gt);} else {i++;}}quickSort3ways(array, low, lt);quickSort3ways(array, gt, high);
}上面这幅图是三向切分的一个例子,为字母进行排序。每次迭代都不会包含和当前基准重复的元素。可以在下图中看到,三向的效率还是有优势的:
(3)算法分析
递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n) ;
最优情况下时间复杂度
快速排序最优的情况就是每一次取到的元素都刚好平分整个数组(很显然我上面的不是);
此时的时间复杂度公式则为:T[n] = 2T[n/2] + f(n);T[n/2]为平分后的子数组的时间复杂度,f[n] 为平分这个数组时所花的时间;
下面来推算下,在最优的情况下快速排序时间复杂度的计算(用迭代法):
T[n] = 2T[n/2] + n ----------------第一次递归
令:n = n/2 = 2 { 2 T[n/4] + (n/2) } + n ----------------第二次递归
= 2^2 T[ n/ (2^2) ] + 2n令:n = n/(2^2) = 2^2 { 2 T[n/ (2^3) ] + n/(2^2)} + 2n ----------------第三次递归 = 2^3 T[ n/ (2^3) ] + 3n...................................................................................... 令:n = n/( 2^(m-1) ) = 2^m T[1] + mn ----------------第m次递归(m次后结束)当最后平分的不能再平分时,也就是说把公式一直往下跌倒,到最后得到T[1]时,说明这个公式已经迭代完了(T[1]是常量了)。得到:T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn;T[n] = 2^m T[1] + mn ;其中m = logn;T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ;其中n为元素个数又因为当n >= 2时:nlogn >= n (也就是logn > 1),所以取后面的 nlogn;综上所述:快速排序最优的情况下时间复杂度为:O( nlogn )最差情况下时间复杂度
最差的情况就是每一次取到的元素就是数组中最小/最大的,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)
这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n;综上所述:快速排序最差的情况下时间复杂度为:O( n^2 )平均时间复杂度
快速排序的平均时间复杂度也是:O(nlogn)
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(nlogn)
7.堆排序
堆排序可以说是一种利用堆的概念来排序的选择排序。
(1)算法简介
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
(2)算法描述和实现
具体算法描述如下:
<1>.将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
<2>.将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
<3>.由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
Java代码实现:
public static void heapSort(int[] array) {buildHeap(array);int n = array.length;int i = 0;// 取出该最大堆的根节点,同时,取最末尾的叶子节点来作为根节点,从此根节点开始调整堆,使其满足最大堆的特性// 直到堆的大小由n个元素降到2个for (i = n - 1; i >= 1; i--) {swap(array, 0, i);heapify(array, 0, i);for (int j = 0; j < array.length; j++) {System.out.print(array[j]);System.out.print(",");}System.out.println();}
}// 构建堆
public static void buildHeap(int[] array) {for (int i = array.length / 2 - 1; i >= 0; i--) {heapify(array, i, array.length);}
}// 调整堆
public static void heapify(int[] data, int parentNode, int heapSize) {int leftChild = 2 * parentNode + 1;// 左子树的下标int rightChild = 2 * parentNode + 2;// 右子树的下标(如果存在的话)int largest = parentNode;// 寻找3个节点中最大值节点的下标if (leftChild < heapSize && data[leftChild] > data[parentNode]) {largest = leftChild;}if (rightChild < heapSize && data[rightChild] > data[largest]) {largest = rightChild;}// 如果最大值不是父节点,那么交换,并继续调整堆if (largest != parentNode) {swap(data, largest, parentNode);heapify(data, largest, heapSize);}
}// 交换函数
public static void swap(int[] array, int i, int j) {int temp = 0;temp = array[i];array[i] = array[j];array[j] = temp;
}堆排序动图演示:
(3)算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
8.计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
(1)算法简介
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
(2)算法描述和实现
具体算法描述如下:
<1>. 得到待排序数的范围(在这里增加了上界和下界);
<2>. 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
<3>. 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加),计算得到每个元素在排序后数组中的结束位置;
<4>. 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
Java代码实现:
public static void countSort(int[] array, int downBound, int upperBound) {int[] countArray = new int[upperBound - downBound + 1];if (upperBound < downBound)return;for (int i = 0; i < array.length; i++) {countArray[array[i] - downBound]++;}int posSum = 0;for (int i = 0; i < upperBound - downBound + 1; i++) {posSum += countArray[i];countArray[i] = posSum;}int[] result = new int[array.length];for (int i = array.length - 1; i >= 0; i--) {result[countArray[array[i] - downBound] - 1] = array[i];countArray[array[i] - downBound]--;}for (int i = 0; i < array.length; i++) {array[i] = result[i];}
}动图演示:
(3)算法分析
当输入的元素是n 个0到k之间的整数时,它的运行时间是 O(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存(如果数据比较分散,则在countArray中其实是有大量0的,占用很多空间)。
最佳情况:T(n) = O(n+k)
最差情况:T(n) = O(n+k)
平均情况:T(n) = O(n+k)
9.桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
(1)算法简介
桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排
(2)算法描述和实现
具体算法描述如下:
<1>.设置一个定量的数组当作空桶;
<2>.遍历输入数据,并且把数据一个一个放到对应的桶里去;
<3>.对每个不是空的桶进行排序;
<4>.从不是空的桶里把排好序的数据拼接起来。
Java代码实现:
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){max = Math.max(max, arr[i]);min = Math.min(min, arr[i]);
}//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());
}//将每个元素放入桶
for(int i = 0; i < arr.length; i++){int num = (arr[i] - min) / (arr.length);bucketArr.get(num).add(arr[i]);
}//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));
}}
桶排序图示(图片来源网络):
关于桶排序更多
(3)算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
最佳情况:T(n) = O(n+k)
最差情况:T(n) = O(n+k)
平均情况:T(n) = O(n2)
10.基数排序
基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;
(1)算法简介
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
(2)算法描述和实现
具体算法描述如下:
<1>.取得数组中的最大数,并取得位数;
<2>.arr为原始数组,从最低位开始取每个位组成radix数组;
<3>.对radix进行计数排序(利用计数排序适用于小范围数的特点);
Java代码实现:
public static void radixSort(int[] array, int maxDigit) {int len = array.length;int digitCount = 1;int digitDev = 1;int[] tmp = new int[len];int[] count = new int[10];while (digitCount <= maxDigit) {Arrays.fill(count, 0);Arrays.fill(count, 0);for (int i = 0; i < len; i++) {count[(array[i] / digitDev) % 10]++;}int sum = 0;for (int i = 1; i < 10; i++) {count[i] = count[i] + count[i - 1];}for (int i = len - 1; i >= 0; i--) {tmp[count[(array[i] / digitDev) % 10] - 1] = array[i];count[(array[i] / digitDev) % 10]--;}for (int i = 0; i < len; i++) {array[i] = tmp[i];}digitDev *= 10;digitCount++;}
}基数排序LSD动图演示:
(3)算法分析
最佳情况:T(n) = O(n * k)
最差情况:T(n) = O(n * k)
平均情况:T(n) = O(n * k)
基数排序有两种方法:
MSD 从高位开始进行排序
LSD 从低位开始进行排序
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶
计数排序:每个桶只存储单一键值
桶排序:每个桶存储一定范围的数值
相关文章:

webkit入门准备
《webkit入门准备》1. Ca) Webkit代码风格b) Inlinec) Constd) 构造与析构e) 重载f) 继承2. 泛式编程a) Vector/List/HashTableb) Iteratorc) 智能指针3. 面向对象编程a) 对象概念b) …

oracle操作
一、导入dmp文件: 1.创建表空间create tablespace 表空间 datafile 路径\文件名.dbf size 1500M autoextend on next 5M maxsize 3000M;注:路径必须为已创建2.创建用户create user 用户名 identified by 密码 default tablespace 表空间;3.更改用户的表空…

一个form表单,多个提交按钮(实现不同功能和地址的提交)
直接上代码 表单部分: <form action"" name"find" method"post" enctype"multipart/form-data"><input type"text" name"name"/><br/><button οnclick"f1()"/>找…

chrome 硬件渲染(GPU Accelerated Compositing in Chrome)
原文链接 http://www.chromium.org/developers/design-documents/gpu-accelerated-compositing-in-chrome chrome 中集成了webkit,这篇文章对webkit 硬件渲染过程有详细的介绍,很好。 简介 这篇文档讲解chrome硬件加速合成的实现细节和背景。 介绍 通常来讲&#…

CCS Font 知识整理总结
总是搞不懂 CCS 中如何正确的使用字体,这下明白了。 1、什么是 font-face font-face 顾名思义,就是文字的脸。字体是文字的外在形式,就是文字的风格,是文字的外衣。比如行书、楷书、草书,都是一种字体。同样一个字每个…

Maven安装与配置(最实用!!!)eclipse中配置maven
Maven安装与配置 一、需要准备的东西 JDKEclipse(本章主要是在eclipse中进行配置maven)Maven程序包 二、下载与安装 1. 前往maven下载最新版的Maven程序: 2. 将文件解压到D:\Program Files\Apache\maven目录下(这样子放目录结…

在Ubuntu 12.04 64bit上配置,安装和运行go程序
注意:下面的安装配置均遵从官网或是教材《Go语言程序设计》中的部分内容. 顺便说下,这是一本很难得的Go语言的入门教程,非常基础和全面。起初我因为这本书的封面比较讨厌它,闲置几年之后,一次偶尔要用时静心翻阅之后,发…
Linux下三个密码生成工具
http://code.csdn.net/news/2820879 想出一个难破解且容易记的密码对不是一件简单的事情。在我为电脑设定一个新密码,或者在线注册了一个新的账号,需要输入密码的时候,脑袋就一片空白。不过,Linux下有几个密码生成工具可以使用&am…

javabean实体类与实体类之间的快速转换
一、Dozer是什么? dozer是一个能把实体和实体之间进行转换的工具.只要建立好映射关系.就像是ORM的数据库和实体映射一样. 使用方法示例如下: // article(PO) -> articleVOArticleVO articleVO dozerMapper.map(article, ArticleVO.class);这段示例代码。将从数…

ATS程序功能和使用方法详解
转载自https://blog.zymlinux.net/index.php/archives/374 Apache Traffic Server的程序文件,与传统的服务器系统有大不同,这里我们将会对这些文件进行详细的解读,并尽可能的对程序的功能和基本用法、参数等进一步说明,以利于新入…

java 读取txt,java读取大文件
java 读取txt,java读取大文件 package com.bbcmart.util; import java.io.File;import java.io.RandomAccessFile;import java.nio.MappedByteBuffer;import java.nio.channels.FileChannel; public class Test { public static void main(String[] args) throws Exception …

Spring Boot整合Spring Data JPA操作数据
一、 Sping Data JPA 简介 Spring Data JPA 是 Spring 基于 ORM 框架、JPA 规范的基础上封装的一套 JPA 应用框架,底层使用了 Hibernate 的 JPA 技术实现,可使开发者用极简的代码即可实现对数据的访问和操作。它提供了包括增删改查等在内的常用功能&…

常用Linux命令总结
常用Linux命令总结 2013-12-08 压缩为gz格式 gzip error_2018082217.log 解压gz格式 gzip -d error_2018082217.log.gz 不解压来搜索gz格式的文件中的匹配行内容 gunzip -c 不真正解压.gz文件,而是检查该文件,不会生成多余的文件 gunzip -c error_20…
调试uIP出现死机问题
在调试uIP,加入http功能时,调试出现死循环 原因是所加入的http文件中含有printf等输出函数,遇到这种情况,有2种解决方法: 1.Keil中勾选“Use MicroLIB” 2. //加入以下代码,支持printf函数,而…

html+spring boot简单的ajax数据传输实现
本篇讲解在前后端不分离情况下的htmlspring boot的项目数据传输实现 首先,后台我写了三个接口 package com.demo.ajax.controller;import com.demo.ajax.Entity.Person; import lombok.extern.slf4j.Slf4j; import org.jboss.logging.Param; import org.springfram…

Tafficserver旁路接入方案综述
转载自 https://blog.zymlinux.net/index.php/archives/821 随着宽带技术的加速普及,目前,几款高性能开源CDN方案在广大开源爱好团队的充分的测试、企业服务应用验证中破壳而出。实际这个地球的互联网用户都在知情与不知情之间使用了ATS的环保服务。这方…

url中去掉index.php,方便redirect()
01 配置文件 return Array( URL_MODEL > 2,); 02 index.php入口文件下面加入文件 .htaccess -->使用editplus-->另存为 <IfModule mod_rewrite.c>RewriteEngine onRewriteCond %{REQUEST_FILENAME} !-dRewriteCond %{REQUEST_FILENAME} !-fRewriteRule ^(.*)$ i…

js校验复选框(多选按钮)是否被选中的方法
js校验复选框是否被选中的方法 方法一:(使用下标进行标记) if ($("#checkbox-id")get(0).checked) {// do something }方法二:(对被选中的进行操作) if($(#checkbox-id).is(:checked)) {// do…

ATS插件开发基础
转载自 https://blog.zymlinux.net/index.php/archives/540 ATS插件开发需要提前了解ATS的插件的一些设计思想,以及系统提供的一些不同方向。我们将会介绍ATS的基础开发知识,以利于后续的插件开发课程讲解。 ATS的SDK文档,是了解ATS的核心设…

NET基础(3):is 和 as 操作符
在C#语言中进行类型转换的另外一种方式是使用is和as操作符。is检查对象是否兼容于指定类型,返回Boolean值true或false。注意,is操作符永远不抛出异常,例如以下代码: Object o new Object();Boolean b1 (o is Object); //返回…

制作大白菜PE盘
大白菜是一款功能非常强大的U盘启动盘制作工具,通过大白菜我们可以把U盘做成可以引导电脑启动的启动盘,同时可以用于装系统或维护系统,虽然制作方法非常简单,不过还是有很多人不懂如何制作大白菜U盘启动盘,这两天我刚好…

为方便ATS管理建立的一些命令别名
转载自https://blog.zymlinux.net/index.php/archives/129 玩ats经常需要切换目录什么感觉敲得麻烦了就建立了一些命令别名,就方便多了。 在用户目录下的.bashrc文件中加入以下内容: alias alogcd /usr/local/var/log/trafficserver;pwd alias atscd /us…

short s1 = 1; s1 = s1 + 1;有错而short s1 = 1; s1 += 1正确
这个问题以前碰到过,也研究过,发表一下: 如果你认为表达式(x i)只是表达式(x x i)的简写方式,这并不准确。这两个表达式都被称为赋值表达式。第二个表达式使用的是简单赋值操作…

pom文件中引入常用的maven仓库
给大家分享几个maven仓库,如果本地总是下载很慢的话可以尝试换一下仓库或者多加几个。可以直接拖放在pom.xml中使用。 阿里云仓库 <mirrors><mirror><id>alimaven</id><name>aliyun maven</name><url>http://maven.ali…

ats新手学习参考
转载自https://blog.zymlinux.net/index.php/archives/129 首先申明本人是个实实在在的菜鸟,现在也只是搭建起来ats玩玩简单的,写本文只是为了给完全的小白一个参考而已。 本人刚开始接触ats的时候,从ats安装到配置也遇到了很多基本的问题&am…
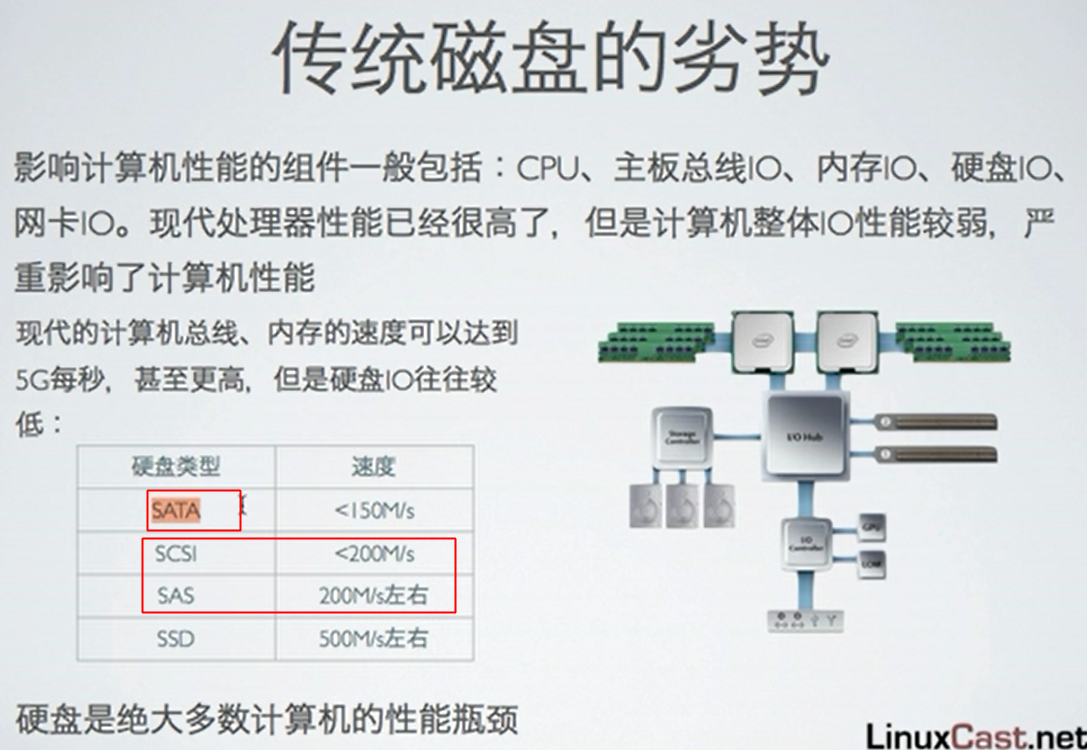
[svc]磁盘接口与RAID
一 磁盘接口 IDE 传统家用: /dev/hda1 SISC 传统服务器: /dev/sdb1 SATA 现在家用 SAS 现在服务器用 FC(光纤通道) 高级服务器 注意: 分区编号,1-4只能给主分区或扩展分区使用,逻辑分区是基于扩展分区来搞的,编号从5开始. MBR分区参考 现在计算机性能瓶颈往往在硬盘: …

条形码?二维码?生成、解析都在这里!
二维码生成与解析 一、生成二维码 二、解析二维码 三、生成一维码 四、全部的代码 五、pom依赖 直接上代码: 一、生成二维码 public class demo {private static final String path1"D:\\code.jpg";private static void qr(String text,int width,int w…

异步预热在线视频实现
转载自https://blog.zymlinux.net/index.php/archives/100 毕业之际给学校搭建了基于ATS的正向代理缓存服务器,专门用来处理优酷土豆等在线视频流量。通过改写一个浏览器做成在线视频专用浏览器,内置了ATS的代理设置。 用php配合memcacheq和小脚本实现了…
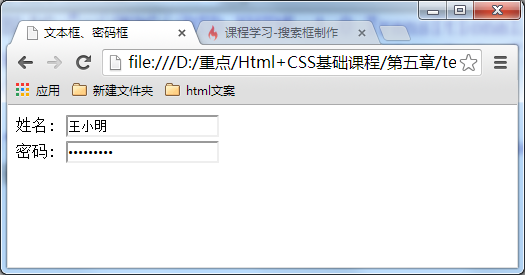
文本输入框、密码输入框
当用户要在表单中键入字母、数字等内容时,就会用到文本输入框。文本框也可以转化为密码输入框。 语法: <form><input type"text/password" name"名称" value"文本" /> </form> 1、type: 当t…

Linux安装mysql,一步到位!
今天在腾讯云上面买了一个服务器,想要把自己的项目部署一下,就要安装mysql,以下是我的安装步骤,在网上有很多人把install敲错了,还有的少-get,种种错误试完之后,我决定发一篇 sudo apt-get install mysql-…